Hostname: page-component-669899f699-g7b4s Total loading time: 0 Render date: 2025-04-25T07:49:06.986Z Has data issue: false hasContentIssue false
  • English
  • Français

The intersection theory of the moduli stack of vector bundles on 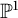$\mathbb {P}^1$

Part of: Families, fibrations Cycles and subschemes

Published online by Cambridge University Press:  07 July 2022

Hannah K. Larson
Hannah K. Larson*
Affiliation:
Department of Mathematics, Stanford University, 380 Jane Stanford Way, Stanford, CA 94305, USA
*
e-mail: hlarson@stanford.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We determine the integral Chow and cohomology rings of the moduli stack 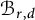$\mathcal {B}_{r,d}$ of rank r, degree d vector bundles on 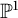$\mathbb {P}^1$ -bundles. We work over a field k of arbitrary characteristic. We first show that the rational Chow ring 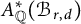$A_{\mathbb {Q}}^*(\mathcal {B}_{r,d})$ is a free 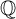$\mathbb {Q}$ -algebra on 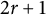$2r+1$ generators. The isomorphism class of this ring happens to be independent of d. Then, we prove that the integral Chow ring 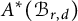$A^*(\mathcal {B}_{r,d})$ is torsion-free and provide multiplicative generators for 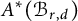$A^*(\mathcal {B}_{r,d})$ as a subring of 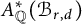$A_{\mathbb {Q}}^*(\mathcal {B}_{r,d})$ . From this description, we see that 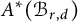$A^*(\mathcal {B}_{r,d})$ is not finitely generated as a 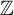$\mathbb {Z}$ -algebra. Finally, when 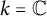$k = \mathbb {C}$ , the cohomology ring of 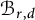$\mathcal {B}_{r,d}$ is isomorphic to its Chow ring.

Keywords

Intersection theorymoduli of vector bundlesChow rings

MSC classification

Primary: 14C15: (Equivariant) Chow groups and rings; motives
Secondary: 14C17: Intersection theory, characteristic classes, intersection multiplicities 14D20: Algebraic moduli problems, moduli of vector bundles
Type
Article
Information
Canadian Mathematical Bulletin , Volume 66 , Issue 2 , June 2023 , pp. 359 - 379
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

During the preparation of this article, the author was supported by the Hertz Foundation and NSF GRFP under Grant No. DGE-1656518.

References

Atiyah, M. F. and Bott, R., The Yang–Mills equations over Riemann surfaces. Philos. Trans. Roy. Soc. Lond. Ser. A 308(1983), no. 1505, 523–615.Google Scholar
Bachmann, T., Affine Grassmannians in ${A}^1$ -homotopy theory, Sel. Math. New Ser. 25(2019), no. 2, Article no. 25, 14 pp.CrossRefGoogle Scholar
Bae, Y. and Schmitt, J., Chow rings of stacks of prestable curves I. Forum Math. Sigma 10(2022), Paper no. e28. arXiv:2012.09887Google Scholar
Bae, Y. and Schmitt, J., Chow rings of stacks of prestable curves II. Preprint, 2021. arXiv:2107.09192 CrossRefGoogle Scholar
Behrend, K. and Dhillon, A., On the motivic class of the stack of bundles . Adv. Math. 212(2007), no. 2, 617–644.CrossRefGoogle Scholar
Bifet, E., Ghione, F., and Letizia, M., On the Abel–Jacobi map for divisors of higher rank on a curve. Math. Ann. 299(1994), no. 4, 641–672.CrossRefGoogle Scholar
Bloch, S., Algebraic cycles and higher K-theory, Adv. Math. 61(1986), no. 3, 267–304.CrossRefGoogle Scholar
Bolognesi, M. and Vistoli, A., Stacks of trigonal curves. Trans. Amer. Math. Soc. 364(2012), no. 7, 3365–3393.CrossRefGoogle Scholar
Bott, R., The space of loops on a Lie group. Michigan Math. J. 5(1958), 35–61.CrossRefGoogle Scholar
Canning, S. and Larson, H., Tautological classes on low-degree Hurwitz spaces. Preprint, 2021. arXiv:2103.09902 Google Scholar
Canning, S. and Larson, H., Chow rings of low-degree Hurwitz spaces. J. Reine Angew. Math., to appear. arXiv:2110.01059 Google Scholar
Edidin, D. and Graham, W., Equivariant intersection theory. Invent. Math. 131(1998), no. 3, 595–634.CrossRefGoogle Scholar
Eisenbud, D. and Harris, J., 3264 and all that: a second course in algebraic geometry, Cambridge University Press, Cambridge, 2016.CrossRefGoogle Scholar
Lam, T. and Shimozono, M., K-double Schur functions and equivariant (co)homology of the affine Grassmannian. Math. Ann. 356(2013), no. 4, 1379–1404.CrossRefGoogle Scholar
Larson, H. K., Universal degeneracy classes for vector bundles on ${\mathbb{P}}^1$ bundles. Adv. Math. 380(2021), 107563, 20 pp.CrossRefGoogle Scholar
Suslin, A. A., Higher Chow groups and etale cohomology . In: Cycles, transfers, and motivic homology theories, Annals of Mathematics Studies, 143, Princeton University Press, Princeton, NJ, 2000, pp. 239–254.Google Scholar
Vistoli, A., Chow groups of quotient varieties. J. Algebra 107(1987), no. 2, 410–424.CrossRefGoogle Scholar