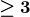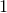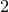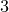1. Introduction
The right framework for a moduli theory of canonical models of varieties of general type was established in [Reference Kollár and Shepherd-BarronKSB88], at least in characteristic
![]() $0$
and over Noetherian bases, both of which we assume from now on. The resulting notion, now called KSB stability, works with finitely presented, flat morphisms
$0$
and over Noetherian bases, both of which we assume from now on. The resulting notion, now called KSB stability, works with finitely presented, flat morphisms
![]() $g:X\to B$
that satisfy three requirements.
$g:X\to B$
that satisfy three requirements.
-
• (Global condition)
 $\omega _{X/B}$
is relatively ample, and
$\omega _{X/B}$
is relatively ample, and
 $g$
is projective,
$g$
is projective, -
• (Fiberwise condition) the fibers
 $X_b$
are semi-log-canonical, and
$X_b$
are semi-log-canonical, and -
• (Local stability condition)
 $\omega _{X/B}^{[m]}$
is flat over
$\omega _{X/B}^{[m]}$
is flat over
 $B$
and commutes with base changes
$B$
and commutes with base changes
 $B^{\prime}\to B$
for every
$B^{\prime}\to B$
for every
 $m\in \mathbb{Z}$
.
$m\in \mathbb{Z}$
.
If
![]() $g$
satisfies the last two, then it is called locally KSB stable. See [Reference KollárKol23] for a detailed discussion of the resulting moduli theory, especially [Reference KollárKol23, Sec. 6.2].
$g$
satisfies the last two, then it is called locally KSB stable. See [Reference KollárKol23] for a detailed discussion of the resulting moduli theory, especially [Reference KollárKol23, Sec. 6.2].
Note that the local stability condition is automatic at codimension
![]() $1$
point and is quite well understood at codimension
$1$
point and is quite well understood at codimension
![]() $2$
points because we have a complete classification of
$2$
points because we have a complete classification of
![]() $2$
-dimensional slc singularities; see [Reference Kollár and Shepherd-BarronKSB88] and [Reference KollárKol23, Sec. 2.2]. Our aim is to show that local stability is automatic in codimension
$2$
-dimensional slc singularities; see [Reference Kollár and Shepherd-BarronKSB88] and [Reference KollárKol23, Sec. 2.2]. Our aim is to show that local stability is automatic in codimension
![]() $\geq 3$
. The simplest version is the following.
$\geq 3$
. The simplest version is the following.
Theorem 1.1.
Let
![]() $g:X\to B$
be a flat morphism of finite type over a field of characteristic 0. Let
$g:X\to B$
be a flat morphism of finite type over a field of characteristic 0. Let
![]() $Z\subset X$
be a closed subset such that
$Z\subset X$
be a closed subset such that
![]() ${\rm codim} (Z_b\subset X_b)\geq 3$
for every
${\rm codim} (Z_b\subset X_b)\geq 3$
for every
![]() $b\in B$
, and set
$b\in B$
, and set
![]() $U:=X\setminus Z$
.
$U:=X\setminus Z$
.
Assume that the fibers
![]() $X_b$
are semi-log-canonical and that
$X_b$
are semi-log-canonical and that
![]() $g \vert _{U}: U\to B$
is locally KSB stable. Then
$g \vert _{U}: U\to B$
is locally KSB stable. Then
![]() $g:X\to B$
is locally KSB stable.
$g:X\to B$
is locally KSB stable.
If the fibers
![]() $X_b$
are CM, the claim follows from [Reference KollárKol23, 10.73]. Being CM is a deformation invariant property for projective, locally stable families by [Reference Kollár and KovácsKK10]; see also [Reference KollárKol23, 2.67]. In particular, the theorem was known to hold for varieties in those connected components of the KSB moduli space that contain a canonical model of a smooth variety.
$X_b$
are CM, the claim follows from [Reference KollárKol23, 10.73]. Being CM is a deformation invariant property for projective, locally stable families by [Reference Kollár and KovácsKK10]; see also [Reference KollárKol23, 2.67]. In particular, the theorem was known to hold for varieties in those connected components of the KSB moduli space that contain a canonical model of a smooth variety.
If
![]() $B$
is reduced, the theorem is proved in [Reference KollárKol13a]; see also [Reference KollárKol23, 5.6]. Thus it remains to deal with the case when
$B$
is reduced, the theorem is proved in [Reference KollárKol13a]; see also [Reference KollárKol23, 5.6]. Thus it remains to deal with the case when
![]() $B={\rm Spec}\, A$
for an Artinian ring
$B={\rm Spec}\, A$
for an Artinian ring
![]() $A$
, which implies the theorem for any
$A$
, which implies the theorem for any
![]() $B$
.
$B$
.
For applications, and even for the proof of Theorem 1.1, we need a form that strengthens it in two significant ways. First, we deal with pairs
![]() $(X,\Delta =\sum a_iD_i)$
, where
$(X,\Delta =\sum a_iD_i)$
, where
![]() $a_i\in \left \{\frac 12, \frac 23, \frac 34, \dots, 1\right \}$
for every
$a_i\in \left \{\frac 12, \frac 23, \frac 34, \dots, 1\right \}$
for every
![]() $i$
; these are frequently called standard coefficients. Second, and this is more important, we assume
$i$
; these are frequently called standard coefficients. Second, and this is more important, we assume
![]() $g$
to be flat only in codimension
$g$
to be flat only in codimension
![]() $\leq 2$
.
$\leq 2$
.
Theorem 1.2.
Let
![]() $g:X\to B$
be a morphism of finite type and of pure relative dimension over a field of characteristic 0, and let
$g:X\to B$
be a morphism of finite type and of pure relative dimension over a field of characteristic 0, and let
![]() $\Delta =\sum a_iD_i$
, where the
$\Delta =\sum a_iD_i$
, where the
![]() $D_i$
are relative Mumford
$D_i$
are relative Mumford
![]() $\mathbb{Z}$
-divisors. Let
$\mathbb{Z}$
-divisors. Let
![]() $Z\subset X$
be a closed subset and set
$Z\subset X$
be a closed subset and set
![]() $U:=X\setminus Z$
. Assume that
$U:=X\setminus Z$
. Assume that
-
(1.2.1)
 $a_i\in \left \{\frac 12, \frac 23, \frac 34, \dots, 1\right \}$
for every
$a_i\in \left \{\frac 12, \frac 23, \frac 34, \dots, 1\right \}$
for every
 $i$
,
$i$
, -
(1.2.2)
 ${\rm codim} (Z_b\subset X_b)\geq 3$
for every
${\rm codim} (Z_b\subset X_b)\geq 3$
for every
 $b\in B$
,
$b\in B$
, -
(1.2.3)
 $g\vert _{U}: U\to B$
is flat and the fibers
$g\vert _{U}: U\to B$
is flat and the fibers
 $(U_b, \Delta |_{U_b})$
are semi-log-canonical,
$(U_b, \Delta |_{U_b})$
are semi-log-canonical,
-
(1.2.4)
 $\omega _{U/B}^{[m]}\bigl (\textstyle{\sum }_i \lfloor{ma_i}\rfloor D_i|_U\bigr )$
is flat over
$\omega _{U/B}^{[m]}\bigl (\textstyle{\sum }_i \lfloor{ma_i}\rfloor D_i|_U\bigr )$
is flat over
 $B$
and commutes with base changes for every
$B$
and commutes with base changes for every
 $m\in \mathbb{Z}$
,
$m\in \mathbb{Z}$
, -
(1.2.5)
 ${\rm depth}_ZX\geq 2$
and
${\rm depth}_ZX\geq 2$
and
-
(1.2.6) the normalization
 $(\overline X_b, \overline C_b+\overline \Delta _b)\to X_b$
is log canonical for every
$(\overline X_b, \overline C_b+\overline \Delta _b)\to X_b$
is log canonical for every
 $b\in B$
, where
$b\in B$
, where
 $\overline C_b$
denotes the conductor of the normalization
$\overline C_b$
denotes the conductor of the normalization
 $\overline X_b\to X_b$
; see [Reference KollárKol13b, 5.2].
$\overline X_b\to X_b$
; see [Reference KollárKol13b, 5.2].
Then
-
(1.2.7)
 $g: X\to B$
is flat,
$g: X\to B$
is flat,
-
(1.2.8) the fibers
 $(X_b, \Delta _b)$
are semi-log-canonical and
$(X_b, \Delta _b)$
are semi-log-canonical and
-
(1.2.9)
 $\omega _{X/B}^{[m]}\bigl (\textstyle{\sum }_i \lfloor{ma_i}\rfloor D_i\bigr )$
is flat over
$\omega _{X/B}^{[m]}\bigl (\textstyle{\sum }_i \lfloor{ma_i}\rfloor D_i\bigr )$
is flat over
 $B$
and commutes with base changes for every
$B$
and commutes with base changes for every
 $m\in \mathbb{Z}$
.
$m\in \mathbb{Z}$
.
Remark 1.3.
-
(1.3.1) As in [Reference KollárKol23, 4.68],
 $D$
is a relative Mumford divisor if at every generic point of
$D$
is a relative Mumford divisor if at every generic point of
 $X_b\cap D$
, the fiber
$X_b\cap D$
, the fiber
 $X_b$
is smooth and
$X_b$
is smooth and
 $D$
is Cartier.
$D$
is Cartier. -
(1.3.2) The notation
 ${\rm depth}_ZX$
stands for
${\rm depth}_ZX$
stands for
 ${\rm depth}_Z\,{\mathscr{O}}_X\colon \!\!\!=\inf \{{\rm depth}_z{\mathscr{O}}_X{\,\vert \,} z\in Z\}$
. This terminology is used, for instance, in [EGA-IV/2, (5.10.1)] and [Reference KollárKol23, 10.3].
${\rm depth}_Z\,{\mathscr{O}}_X\colon \!\!\!=\inf \{{\rm depth}_z{\mathscr{O}}_X{\,\vert \,} z\in Z\}$
. This terminology is used, for instance, in [EGA-IV/2, (5.10.1)] and [Reference KollárKol23, 10.3]. -
(1.3.3) The condition (1.2.5) is easy to ensure by replacing
 ${\mathscr{O}}_X$
with the push-forward of
${\mathscr{O}}_X$
with the push-forward of
 ${\mathscr{O}}_{U}$
if necessary. If
${\mathscr{O}}_{U}$
if necessary. If
 $B$
is
$B$
is
 $S_2$
then (1.2.5) holds iff
$S_2$
then (1.2.5) holds iff
 $X$
is
$X$
is
 $S_2$
.
$S_2$
. -
(1.3.4) Assumption (1.2.6) is a weakening of the fiberwise condition; the two are equivalent iff
 $X_b$
is
$X_b$
is
 $S_2$
. In many applications, including the proof of Theorem 1.2, at the beginning we know only (1.2.6), but we eventually conclude that
$S_2$
. In many applications, including the proof of Theorem 1.2, at the beginning we know only (1.2.6), but we eventually conclude that
 $(X_b,\Delta _b)$
is slc.
$(X_b,\Delta _b)$
is slc. -
(1.3.5) The following may be a better way of formulating (1.2.6). Let
 $j:U\hookrightarrow X$
be the natural embedding, and set
$j:U\hookrightarrow X$
be the natural embedding, and set
 $\widetilde X_b:={\rm Spec}_{X_b}\,j_*{\mathscr{O}}_{U_b}$
, which is the demi-normalization and also the
$\widetilde X_b:={\rm Spec}_{X_b}\,j_*{\mathscr{O}}_{U_b}$
, which is the demi-normalization and also the
 $S_2$
-hull of the fiber
$S_2$
-hull of the fiber
 $X_b$
; see [Reference KollárKol13b, Sec. 5.1] and [Reference KollárKol23, Sec. 9.1]. Then
$X_b$
; see [Reference KollárKol13b, Sec. 5.1] and [Reference KollárKol23, Sec. 9.1]. Then
 $\widetilde X_b\to X_b$
is a universal homeomorphism that is an isomorphism over
$\widetilde X_b\to X_b$
is a universal homeomorphism that is an isomorphism over
 $U_b$
. Now (1.2.6) holds iff the induced pair
$U_b$
. Now (1.2.6) holds iff the induced pair
 $\bigl (\widetilde X_b, \widetilde \Delta _b\bigr )$
is slc.
$\bigl (\widetilde X_b, \widetilde \Delta _b\bigr )$
is slc. -
(1.3.6) If
 $a_i\in \left \{\frac 23, \frac 34, \dots \right \}$
, then (1.2.4) is the same as the main assumption of KSB stabilty, with standard coefficients as defined in [Reference KollárKol23, 6.21.3].
$a_i\in \left \{\frac 23, \frac 34, \dots \right \}$
, then (1.2.4) is the same as the main assumption of KSB stabilty, with standard coefficients as defined in [Reference KollárKol23, 6.21.3].If we allow
 $a_i=\frac 12$
, then the above definition treats the pairs
$a_i=\frac 12$
, then the above definition treats the pairs
 $(X, D)$
,
$(X, D)$
,
 $(X, \frac 12 D+\frac 12 D)$
and
$(X, \frac 12 D+\frac 12 D)$
and
 $(X, \frac 12 (2D))$
as different objects. Note that
$(X, \frac 12 (2D))$
as different objects. Note that
 $\omega _X(\sum \lfloor{a_i}\rfloor D_i)$
is
$\omega _X(\sum \lfloor{a_i}\rfloor D_i)$
is
 $\omega _X(D)$
in the first case but is
$\omega _X(D)$
in the first case but is
 $\omega _X$
in the other two cases. Thus, replacing
$\omega _X$
in the other two cases. Thus, replacing
 $1\cdot D_i$
with
$1\cdot D_i$
with
 $\frac 12 D_i+\frac 12 D_i$
ensures the extra condition on the
$\frac 12 D_i+\frac 12 D_i$
ensures the extra condition on the
 $\{D_i\colon a_i=1\}$
in [Reference KollárKol23, 6.22.3].
$\{D_i\colon a_i=1\}$
in [Reference KollárKol23, 6.22.3].This way of handling the coefficient
 $\frac 12$
case may not be natural from the point of view of moduli, but it seems necessary; see [Reference KollárKol23, Secs. 8.1–2] for a discussion of the general notion of such marked pairs.
$\frac 12$
case may not be natural from the point of view of moduli, but it seems necessary; see [Reference KollárKol23, Secs. 8.1–2] for a discussion of the general notion of such marked pairs. -
(1.3.7) The definition of KSB stabilty with standard coefficients also requires the
 $D_i$
to be flat by [Reference KollárKol23, 6.21.1]. We do not know whether this is automatic in codimensions
$D_i$
to be flat by [Reference KollárKol23, 6.21.1]. We do not know whether this is automatic in codimensions
 $\geq 3$
; see Corollary 4.3 for a special case.
$\geq 3$
; see Corollary 4.3 for a special case. -
(1.3.8) We comment on other versions of stability in Section 5.
§1.4 Sketch of an approach to Theorem 1.2.Assume for simplicity that we are over
![]() $\mathbb{C}$
,
$\mathbb{C}$
,
![]() $B={\rm Spec}\, A$
for an Artinian ring
$B={\rm Spec}\, A$
for an Artinian ring
![]() $A$
and that the closed fiber
$A$
and that the closed fiber
![]() $X_k$
is projective. As in [Reference Kollár and KovácsKK10], the proof relies on the Du Bois property (see Remark 1.9) of slc varieties, which implies that the natural maps
$X_k$
is projective. As in [Reference Kollár and KovácsKK10], the proof relies on the Du Bois property (see Remark 1.9) of slc varieties, which implies that the natural maps
If
![]() $g$
is also flat, these imply that the
$g$
is also flat, these imply that the
![]() $R^ig_*{\mathscr{O}}_X$
are (locally) free by [Reference Du Bois and JarraudDJ74]. Using this for various cyclic covers, [Reference KollárKol23, 2.68] shows that
$R^ig_*{\mathscr{O}}_X$
are (locally) free by [Reference Du Bois and JarraudDJ74]. Using this for various cyclic covers, [Reference KollárKol23, 2.68] shows that
![]() $\omega _{X/B}$
is flat over
$\omega _{X/B}$
is flat over
![]() $B$
and commutes with base changes
$B$
and commutes with base changes
![]() $B^{\prime}\to B$
.
$B^{\prime}\to B$
.
An inspection of these proofs shows that, in order to get the flatness of
![]() $\omega _{X/B}$
, we need (1.4.1) only for
$\omega _{X/B}$
, we need (1.4.1) only for
![]() $i=n,n{-}1$
, where
$i=n,n{-}1$
, where
![]() $n:=\dim X_k$
. This is where the codimension
$n:=\dim X_k$
. This is where the codimension
![]() $3$
condition enters first. As we noted in (1.3.5), the demi-normalization
$3$
condition enters first. As we noted in (1.3.5), the demi-normalization
![]() $\widetilde X_k$
of
$\widetilde X_k$
of
![]() $X_k$
is slc, and
$X_k$
is slc, and
![]() $\widetilde X_k\to X_k$
is a universal homeomorphism that is an isomorphism over
$\widetilde X_k\to X_k$
is a universal homeomorphism that is an isomorphism over
![]() $U_k$
. Thus
$U_k$
. Thus
 \begin{align*} H^i(X_k^{\mathrm {an}}, \mathbb {C}) & \simeq H^i(\widetilde X_k^{\mathrm {an}}, \mathbb {C}) \quad \mbox {for every $i$, and}\\ H^i(X_k^{\mathrm {an}}, {\mathscr {O}}_{X_k^{\mathrm {an}}}) &\simeq H^i(\widetilde X_k^{\mathrm {an}}, {\mathscr {O}}_{\widetilde X_k^{\mathrm {an}}}) \quad \mbox {for $i=n,n{-}1$.}\end{align*}
\begin{align*} H^i(X_k^{\mathrm {an}}, \mathbb {C}) & \simeq H^i(\widetilde X_k^{\mathrm {an}}, \mathbb {C}) \quad \mbox {for every $i$, and}\\ H^i(X_k^{\mathrm {an}}, {\mathscr {O}}_{X_k^{\mathrm {an}}}) &\simeq H^i(\widetilde X_k^{\mathrm {an}}, {\mathscr {O}}_{\widetilde X_k^{\mathrm {an}}}) \quad \mbox {for $i=n,n{-}1$.}\end{align*}
It follows that (1.4.1) holds for
![]() $i=n,n{-}1$
, although
$i=n,n{-}1$
, although
![]() $X_k$
is not (yet known to be) Du Bois; see also Theorem 4.2. One also sees that it is enough if
$X_k$
is not (yet known to be) Du Bois; see also Theorem 4.2. One also sees that it is enough if
![]() $g$
is flat at points of dimension
$g$
is flat at points of dimension
![]() $\geq n-2$
. Therefore we get that
$\geq n-2$
. Therefore we get that
![]() $\omega _{X/B}$
is flat over
$\omega _{X/B}$
is flat over
![]() $B$
.
$B$
.
Interestingly, this approach does not seem to imply that
![]() $X$
is flat over
$X$
is flat over
![]() $B$
, much less the full Theorem 1.2. A possible explanation is that
$B$
, much less the full Theorem 1.2. A possible explanation is that
![]() $\omega _X$
is insensitive to codimension 2:
$\omega _X$
is insensitive to codimension 2:
Lemma 1.5.
Let
![]() $\pi :Y\to X$
be a quasi-finite morphism that is an isomorphism at points of codimension
$\pi :Y\to X$
be a quasi-finite morphism that is an isomorphism at points of codimension
![]() $\leq 1$
. Then
$\leq 1$
. Then
![]() $\pi _*\omega _Y\simeq \omega _X$
.
$\pi _*\omega _Y\simeq \omega _X$
.
Proof.
Let
![]() $\imath : U\hookrightarrow X$
be the largest open subset such that
$\imath : U\hookrightarrow X$
be the largest open subset such that
![]() $\pi ^{\prime}\colon \!\!\!=\pi \vert _{\pi ^{-1}U}$
is an isomorphism between
$\pi ^{\prime}\colon \!\!\!=\pi \vert _{\pi ^{-1}U}$
is an isomorphism between
![]() $\pi ^{-1}U$
and
$\pi ^{-1}U$
and
![]() $U$
. Let
$U$
. Let
![]() $\jmath : \pi ^{-1}U\hookrightarrow Y$
denote the embedding. By assumption
$\jmath : \pi ^{-1}U\hookrightarrow Y$
denote the embedding. By assumption
![]() ${\rm codim}(Y\setminus \pi ^{-1}U,Y)\geq 2$
and
${\rm codim}(Y\setminus \pi ^{-1}U,Y)\geq 2$
and
![]() ${\rm codim}(X\setminus U,X)\geq 2$
. Therefore, because
${\rm codim}(X\setminus U,X)\geq 2$
. Therefore, because
![]() $\omega _X$
and
$\omega _X$
and
![]() $\omega _Y$
are
$\omega _Y$
are
![]() $S_2$
-sheaves (cf. [Reference Kollár and MoriKM98, 5.69]), it follows that
$S_2$
-sheaves (cf. [Reference Kollár and MoriKM98, 5.69]), it follows that
In order to prove Theorem 1.2, we use the techniques of [Reference Kollár and KovácsKK20], and establish the following local, Du Bois version (see Remark 1.9).
Theorem 1.6.
Let
![]() $B$
be a local scheme over a field of characteristic
$B$
be a local scheme over a field of characteristic
![]() $0$
, and let
$0$
, and let
![]() $f:(X,x)\to B$
be a local morphism that is essentially of finite type. Let
$f:(X,x)\to B$
be a local morphism that is essentially of finite type. Let
![]() $X_{k}$
be the fiber of
$X_{k}$
be the fiber of
![]() $f$
over the closed point of
$f$
over the closed point of
![]() $B$
, let
$B$
, let
![]() $Z\subseteq X_{k}$
be a closed subset of codimension
$Z\subseteq X_{k}$
be a closed subset of codimension
![]() $\geq 3$
, and set
$\geq 3$
, and set
![]() $\jmath :U_{k}\colon \!\!\!= X_{k}\setminus Z\hookrightarrow X_{k}$
. Assume that
$\jmath :U_{k}\colon \!\!\!= X_{k}\setminus Z\hookrightarrow X_{k}$
. Assume that
-
(1.6.1)
 $f$
is flat along
$f$
is flat along
 $U_{k}$
, and
$U_{k}$
, and
-
(1.6.2)
 ${\rm Spec} \jmath _*{\mathscr{O}}_{U_{k}}$
is Du Bois.
${\rm Spec} \jmath _*{\mathscr{O}}_{U_{k}}$
is Du Bois.
Then
![]() $\omega _{X/B}$
is flat over
$\omega _{X/B}$
is flat over
![]() $B$
and commutes with arbitrary base change.
$B$
and commutes with arbitrary base change.
Theorem 1.6 will be proved as a combination of Theorem 3.16 and Theorem 4.2.
As before, the method does not seem to imply that
![]() $X$
is flat over
$X$
is flat over
![]() ${\rm Spec}\, S$
, not even if we assume that
${\rm Spec}\, S$
, not even if we assume that
![]() ${\rm depth}_ZX\geq 2$
, as in (1.2.5). However, we do not have a counterexample.
${\rm depth}_ZX\geq 2$
, as in (1.2.5). However, we do not have a counterexample.
Note that, without the Du Bois assumption, such examples are easy to get:
Example 1.7. Let
![]() $\{C_i:i\in I\}$
be a finite set of smooth, projective curves. Fix
$\{C_i:i\in I\}$
be a finite set of smooth, projective curves. Fix
![]() $d_i\gt 0$
such that
$d_i\gt 0$
such that
![]() $d_i\leq \deg \omega _{C_i}$
for some
$d_i\leq \deg \omega _{C_i}$
for some
![]() $i\in I$
and that
$i\in I$
and that
![]() $d_j\gt \deg \omega _{C_j}$
for some
$d_j\gt \deg \omega _{C_j}$
for some
![]() $j\in I$
. Set
$j\in I$
. Set
![]() $Y:=\times _i C_i$
and consider a line bundle
$Y:=\times _i C_i$
and consider a line bundle
![]() $L=\boxtimes _i L_i$
on
$L=\boxtimes _i L_i$
on
![]() $Y$
, where
$Y$
, where
![]() $\deg L_i=d_i$
.
$\deg L_i=d_i$
.
The affine cone over
![]() $Y$
with conormal bundle
$Y$
with conormal bundle
![]() $L$
(cf. [Reference KollárKol13b, 3.8]) is
$L$
(cf. [Reference KollárKol13b, 3.8]) is
By the
![]() $i=0$
case of [Reference KollárKol13b, 3.13.2], its dualizing sheaf is the sheafification of the module
$i=0$
case of [Reference KollárKol13b, 3.13.2], its dualizing sheaf is the sheafification of the module
The
![]() $m$
th graded pieces are
$m$
th graded pieces are
Note that if
![]() $d_i\leq \deg \omega _{C_i}$
then
$d_i\leq \deg \omega _{C_i}$
then
![]() $h^0(C_i, L_i)$
depends on the choice of
$h^0(C_i, L_i)$
depends on the choice of
![]() $L_i$
, not only on
$L_i$
, not only on
![]() $\deg L_i$
.
$\deg L_i$
.
By contrast, we claim that
![]() $h^0(Y, \omega _Y\otimes L^m)$
depends only on the degrees of the
$h^0(Y, \omega _Y\otimes L^m)$
depends only on the degrees of the
![]() $L_i$
and the
$L_i$
and the
![]() $m$
. Indeed, if
$m$
. Indeed, if
![]() $m\leq -1$
then
$m\leq -1$
then
![]() $\omega _{C_j}\otimes L_j^m$
has negative degree, so
$\omega _{C_j}\otimes L_j^m$
has negative degree, so
![]() $H^0(Y, \omega _Y\otimes L^m)=0$
. If
$H^0(Y, \omega _Y\otimes L^m)=0$
. If
![]() $m=0$
then there is no dependence on the
$m=0$
then there is no dependence on the
![]() $L_i$
, and for
$L_i$
, and for
![]() $m\geq 1$
$m\geq 1$
Now set
![]() $B:= \times _i {\rm Pic}^{d_i}(C_i)$
, and note that
$B:= \times _i {\rm Pic}^{d_i}(C_i)$
, and note that
![]() $Y\times B\simeq \times _i\left (C_i\times {\rm Pic}^{d_i}(C_i)\right )$
. Let
$Y\times B\simeq \times _i\left (C_i\times {\rm Pic}^{d_i}(C_i)\right )$
. Let
![]() $P_i$
denote the universal degree
$P_i$
denote the universal degree
![]() $d_i$
line bundle on
$d_i$
line bundle on
![]() $C_i\times {\rm Pic}^{d_i}(C_i)$
, and let
$C_i\times {\rm Pic}^{d_i}(C_i)$
, and let
![]() $P=\boxtimes P_i$
on
$P=\boxtimes P_i$
on
![]() $Y\times B$
. Further, let
$Y\times B$
. Further, let
![]() $\pi :Y\times B\to B$
be the projection, and consider the universal cone
$\pi :Y\times B\to B$
be the projection, and consider the universal cone
over
![]() $B$
. As we noted, the
$B$
. As we noted, the
![]() $h^0\bigl (Y, \omega _Y\otimes P_b^m\bigr )$
are independent of
$h^0\bigl (Y, \omega _Y\otimes P_b^m\bigr )$
are independent of
![]() $b\in B$
, so the dualizing sheaf of
$b\in B$
, so the dualizing sheaf of
![]() $X_B$
is flat over
$X_B$
is flat over
![]() $B$
. However,
$B$
. However,
![]() $h^0\bigl (Y, P_b\bigr )$
does depend on
$h^0\bigl (Y, P_b\bigr )$
does depend on
![]() $b\in B$
; thus the structure sheaf is not flat over
$b\in B$
; thus the structure sheaf is not flat over
![]() $B$
. Note that
$B$
. Note that
![]() $h^1\bigl (Y, P_b\bigr )$
also depends on
$h^1\bigl (Y, P_b\bigr )$
also depends on
![]() $b\in B$
, and when
$b\in B$
, and when
![]() $h^1\bigl (Y, P_b\bigr )\neq 0$
, then
$h^1\bigl (Y, P_b\bigr )\neq 0$
, then
![]() $C_a(Y,P_b)$
, the normalization of the fiber of
$C_a(Y,P_b)$
, the normalization of the fiber of
![]() $X_B$
over
$X_B$
over
![]() $b$
, is not Du Bois by [Reference Graf and KovácsGK14, 2.5].
$b$
, is not Du Bois by [Reference Graf and KovácsGK14, 2.5].
We also prove that KSB stability is automatic in codimension
![]() $3$
in a different manner, namely, that it is enough to check it on general hyperplane sections.
$3$
in a different manner, namely, that it is enough to check it on general hyperplane sections.
Corollary 1.8.
Let
![]() $g:X\to B$
be a quasi-projective morphism of pure relative dimension
$g:X\to B$
be a quasi-projective morphism of pure relative dimension
![]() $n\geq 3$
over a field of characteristic 0, and
$n\geq 3$
over a field of characteristic 0, and
![]() $\Delta =\sum a_iD_i$
, where the
$\Delta =\sum a_iD_i$
, where the
![]() $D_i$
are relative Mumford
$D_i$
are relative Mumford
![]() $\mathbb{Z}$
-divisors. Assume that
$\mathbb{Z}$
-divisors. Assume that
-
(1.8.1)
 $a_i\in \left \{\frac 12, \frac 23, \frac 34, \dots, 1\right \}$
for every
$a_i\in \left \{\frac 12, \frac 23, \frac 34, \dots, 1\right \}$
for every
 $i$
,
$i$
, -
(1.8.2)
 ${\rm depth}_x\ X\geq \min \bigl \{2, {\rm codim} (x, g^{-1}(g(x))\bigr \}$
for every
${\rm depth}_x\ X\geq \min \bigl \{2, {\rm codim} (x, g^{-1}(g(x))\bigr \}$
for every
 $x\in X$
,
$x\in X$
, -
(1.8.3) the normalization
 $(\overline X_b, \overline C_b+\overline \Delta _b)\to X_b$
is log canonical for every
$(\overline X_b, \overline C_b+\overline \Delta _b)\to X_b$
is log canonical for every
 $b\in B$
and
$b\in B$
and
-
(1.8.4) general relative surface sections of
 $(X, \Delta )\to B$
are locally KSB stable.
$(X, \Delta )\to B$
are locally KSB stable.
Proof.
By [Reference KollárKol23, 9.17] we may assume that
![]() $B$
is Artinian. Then the relative pluricanonical sheaves
$B$
is Artinian. Then the relative pluricanonical sheaves
![]() $\omega _{X/B}^{[m]}\bigl (\textstyle{\sum }_i \lfloor{ma_i}\rfloor D_i\bigr )$
are
$\omega _{X/B}^{[m]}\bigl (\textstyle{\sum }_i \lfloor{ma_i}\rfloor D_i\bigr )$
are
![]() $S_2$
. This continues to hold after first tensoring with line bundles and then restricting to general surface sections
$S_2$
. This continues to hold after first tensoring with line bundles and then restricting to general surface sections
![]() $Y:=H_1\cap \cdots H_{n-2}\subset X$
; for the latter, see [Reference KollárKol23, 10.18]. Thus
$Y:=H_1\cap \cdots H_{n-2}\subset X$
; for the latter, see [Reference KollárKol23, 10.18]. Thus
Now by [Reference MatsumuraMat89, p.177] or [Reference KollárKol23, 10.56], the
![]() $\omega _{X/B}^{[m]}\bigl (\textstyle{\sum }_i \lfloor{ma_i}\rfloor D_i\bigr )$
are flat over
$\omega _{X/B}^{[m]}\bigl (\textstyle{\sum }_i \lfloor{ma_i}\rfloor D_i\bigr )$
are flat over
![]() $B$
outside a subset of codimesion
$B$
outside a subset of codimesion
![]() $\geq 3$
. Thus they are flat everywhere by Theorem 1.2. Over Artin rings, flat modules are free [StacksProject, Tag 051G], so commuting with base change holds; see also [Reference KollárKol23, 9.17].
$\geq 3$
. Thus they are flat everywhere by Theorem 1.2. Over Artin rings, flat modules are free [StacksProject, Tag 051G], so commuting with base change holds; see also [Reference KollárKol23, 9.17].
Remark 1.9. The precise definition of Du Bois singularities, introduced by Steenbrink [Reference SteenbrinkSte83], is quite involved. It starts with the construction of the Du Bois complex; see [Reference Du BoisDB81, Reference Guillén, Navarro Aznar, Pascual Gainza and PuertaGNPP88], which has a natural filtration and agrees with the usual de Rham complex if
![]() $X$
is nonsingular. For our purposes the important part is the
$X$
is nonsingular. For our purposes the important part is the
![]() $0^{{th}}$
associated graded Du Bois complex of
$0^{{th}}$
associated graded Du Bois complex of
![]() $X$
, which is denoted by
$X$
, which is denoted by
![]() $\underline{\Omega }_{X}^0$
. This comes with the natural morphism
$\underline{\Omega }_{X}^0$
. This comes with the natural morphism
![]() ${\mathscr{O}}_X\to \underline{\Omega }_{X}^0$
, and a separated scheme of finite type over
${\mathscr{O}}_X\to \underline{\Omega }_{X}^0$
, and a separated scheme of finite type over
![]() $\mathbb{C}$
is said to have Du Bois singularities if this natural morphism is a quasi-isomorphism. For more details on the definition of Du Bois singularities and their relevance to higher dimensional geometry, see [Reference KollárKol13b, Chap.6].
$\mathbb{C}$
is said to have Du Bois singularities if this natural morphism is a quasi-isomorphism. For more details on the definition of Du Bois singularities and their relevance to higher dimensional geometry, see [Reference KollárKol13b, Chap.6].
As we already mentioned in (1.4.1), for a proper complex variety
![]() $X$
with Du Bois singularities, the natural morphism
$X$
with Du Bois singularities, the natural morphism
is surjective. (At least heuristically, one may think of Du Bois singularities as the largest class for which this holds, cf. [Reference KovácsKov12].)
The surjectivity in (1.9.1) enables one to use topological arguments to control the sheaf cohomology groups
![]() $H^i(X,{\mathscr{O}}_X)$
. It is a key element of Kodaira-type vanishing theorems [Reference KollárKol87, Reference KollárKol95, Sec. 12, Reference KovácsKov00, Reference Kovács, Schwede and SmithKSS10] and leads to various results on deformations of Du Bois schemes [Reference Du Bois and JarraudDJ74, Reference Kollár and KovácsKK10, Reference Kovács and SchwedeKS16b].
$H^i(X,{\mathscr{O}}_X)$
. It is a key element of Kodaira-type vanishing theorems [Reference KollárKol87, Reference KollárKol95, Sec. 12, Reference KovácsKov00, Reference Kovács, Schwede and SmithKSS10] and leads to various results on deformations of Du Bois schemes [Reference Du Bois and JarraudDJ74, Reference Kollár and KovácsKK10, Reference Kovács and SchwedeKS16b].
The obvious candidate for a local analog of (1.4.1) is the map on local cohomologies
However, this map is never surjective for
![]() $i=\dim X$
. In fact, if
$i=\dim X$
. In fact, if
![]() $X$
is smooth of dimension
$X$
is smooth of dimension
![]() $n\geq 2$
, then
$n\geq 2$
, then
![]() $H^n_x(X^{{\rm an}}, \mathbb{C})$
is trivial, but
$H^n_x(X^{{\rm an}}, \mathbb{C})$
is trivial, but
![]() $H^n_x(X^{{\rm an}},{\mathscr{O}}_{X^{{\rm an}}})$
is infinite dimensional.
$H^n_x(X^{{\rm an}},{\mathscr{O}}_{X^{{\rm an}}})$
is infinite dimensional.
To get the right notion, one should look at the natural morphisms
The general theory implies that the composition
![]() $\varrho {\circ} \sigma$
induces surjectivity on (hyper)cohomology for any proper
$\varrho {\circ} \sigma$
induces surjectivity on (hyper)cohomology for any proper
![]() $X$
. If
$X$
. If
![]() $X$
has Du Bois singularities, then
$X$
has Du Bois singularities, then
![]() $\varrho$
is a quasi-isomorphism, and the surjectivity in (1.9.1) follows.
$\varrho$
is a quasi-isomorphism, and the surjectivity in (1.9.1) follows.
Note that
![]() $\varrho$
may be represented by a map between coherent sheaves; thus it is possible to work with
$\varrho$
may be represented by a map between coherent sheaves; thus it is possible to work with
![]() $\varrho$
entirely algebraically. Eventually, this suggests that the correct local replacement of (1.4.1) is the (a priori stronger) quasi-isomorphism of
$\varrho$
entirely algebraically. Eventually, this suggests that the correct local replacement of (1.4.1) is the (a priori stronger) quasi-isomorphism of
![]() $\varrho$
; see also [Reference KovácsKov99, Lemma 2.2]. This turns out to be equivalent to the local Du Bois isomorphisms
$\varrho$
; see also [Reference KovácsKov99, Lemma 2.2]. This turns out to be equivalent to the local Du Bois isomorphisms
At the end this leads to the local cohomology lifting property, the key technical ingredient in [Reference Kollár and KovácsKK20]; see Definition 3.2.
Notation 1.10.
![]() $\mathbb{H}^i$
stands for
$\mathbb{H}^i$
stands for
![]() ${\mathcal{R}}^{\,i}\Gamma$
, the
${\mathcal{R}}^{\,i}\Gamma$
, the
![]() $i^{{th}}$
derived functor of
$i^{{th}}$
derived functor of
![]() $\Gamma$
, the functor of sections; and
$\Gamma$
, the functor of sections; and
![]() $\mathbb{H}^i_x$
stands for
$\mathbb{H}^i_x$
stands for
![]() ${\mathcal{R}}^{\,i}\Gamma _x$
, the
${\mathcal{R}}^{\,i}\Gamma _x$
, the
![]() $i^{{th}}$
derived functor
$i^{{th}}$
derived functor
![]() $\Gamma _x$
, the functor of sections with support at
$\Gamma _x$
, the functor of sections with support at
![]() $x$
, i.e., the
$x$
, i.e., the
![]() $i^{{th}}$
local cohomology functor with support at
$i^{{th}}$
local cohomology functor with support at
![]() $x$
on the derived category of quasi-coherent sheaves on
$x$
on the derived category of quasi-coherent sheaves on
![]() $X$
.
$X$
.
2. Filtrations on modules over Artinian local rings
We recall the following notation from [Reference Kollár and KovácsKK20].
2.1 Maximal filtrations
Let
![]() $(S,\mathfrak{m}, k)$
be an Artinian local ring and let
$(S,\mathfrak{m}, k)$
be an Artinian local ring and let
![]() $N$
be a finite
$N$
be a finite
![]() $S$
-module with a filtration
$S$
-module with a filtration
![]() $N= N_0\supsetneq N_1\supsetneq \dots \supsetneq N_{q} \supsetneq N_{q+1}=0$
such that
$N= N_0\supsetneq N_1\supsetneq \dots \supsetneq N_{q} \supsetneq N_{q+1}=0$
such that
![]() ${N_{j}}\Big /{N_{j+1}} \simeq k$
as
${N_{j}}\Big /{N_{j+1}} \simeq k$
as
![]() $S$
-modules for each
$S$
-modules for each
![]() $j=0,\dots, q$
. Further, let
$j=0,\dots, q$
. Further, let
![]() $f:(X,x)\to ({\rm Spec}\, S,\mathfrak{m})$
be a local morphism, and denote the fiber of
$f:(X,x)\to ({\rm Spec}\, S,\mathfrak{m})$
be a local morphism, and denote the fiber of
![]() $f$
over
$f$
over
![]() $\mathfrak{m}$
by
$\mathfrak{m}$
by
![]() $X_{k}$
. It then follows that for each
$X_{k}$
. It then follows that for each
![]() $j=0,\dots, q$
,
$j=0,\dots, q$
,
2.2 Filtering
 $S$
$S$
In particular, considering
![]() $S$
as a module over itself, we choose a filtration of
$S$
as a module over itself, we choose a filtration of
![]() $S$
by ideals
$S$
by ideals
![]() $S=I_0\supsetneq I_1\supsetneq \dots \supsetneq I_{q} \supsetneq I_{q+1}=0$
such that
$S=I_0\supsetneq I_1\supsetneq \dots \supsetneq I_{q} \supsetneq I_{q+1}=0$
such that
![]() ${I_{j}}\Big /{I_{j+1}} \simeq k$
as
${I_{j}}\Big /{I_{j+1}} \simeq k$
as
![]() $S$
-modules for all
$S$
-modules for all
![]() $0\leq j\leq q$
. Observe that in this case,
$0\leq j\leq q$
. Observe that in this case,
![]() $I_{1}=\mathfrak{m}$
and for every
$I_{1}=\mathfrak{m}$
and for every
![]() $j$
there exists a
$j$
there exists a
![]() $t_j\in I_j$
such that the composition
$t_j\in I_j$
such that the composition
![]() $S\stackrel{t_j \cdot }\longrightarrow I_j \longrightarrow{I_j}\Big /{I_{j+1}}$
induces an isomorphism
$S\stackrel{t_j \cdot }\longrightarrow I_j \longrightarrow{I_j}\Big /{I_{j+1}}$
induces an isomorphism
![]() $S\Big /\mathfrak{m}\simeq{I_j}\Big /{I_{j+1}}$
. In particular,
$S\Big /\mathfrak{m}\simeq{I_j}\Big /{I_{j+1}}$
. In particular,
![]() $\mathcal{ann}\left ({I_j}\Big /{I_{j+1}}\right ) =\mathfrak{m}$
. Finally, let
$\mathcal{ann}\left ({I_j}\Big /{I_{j+1}}\right ) =\mathfrak{m}$
. Finally, let
![]() $S_j:= S\Big /{I_j}$
. Note that
$S_j:= S\Big /{I_j}$
. Note that
![]() $S_1= S\Big /\mathfrak{m}$
and
$S_1= S\Big /\mathfrak{m}$
and
![]() $S_{q+1}=S$
.
$S_{q+1}=S$
.
2.3 Filtering
 $\boldsymbol{\omega} _{\textbf{\textit{S}}}$
$\boldsymbol{\omega} _{\textbf{\textit{S}}}$
Applying Grothendieck duality to the closed embedding given by the surjection
![]() $S\twoheadrightarrow S_j$
implies that
$S\twoheadrightarrow S_j$
implies that
![]() $\omega _{S_j} \simeq{{\rm Hom}}_S(S_j, \omega _S)$
, and we obtain injective
$\omega _{S_j} \simeq{{\rm Hom}}_S(S_j, \omega _S)$
, and we obtain injective
![]() $S$
-module homomorphisms
$S$
-module homomorphisms
![]() $\varsigma _j: \omega _{S_j} \hookrightarrow \omega _{S_{j+1}}$
induced by the natural surjection
$\varsigma _j: \omega _{S_j} \hookrightarrow \omega _{S_{j+1}}$
induced by the natural surjection
![]() $S_{j+1}\twoheadrightarrow S_j$
. Using the fact that the canonical module of an Arinian local ring, in particular
$S_{j+1}\twoheadrightarrow S_j$
. Using the fact that the canonical module of an Arinian local ring, in particular
![]() $\omega _S$
, is an injective module and applying the functor
$\omega _S$
, is an injective module and applying the functor
![]() ${{\rm Hom}}_S(\_\_, \omega _S)$
to the short exact sequence of
${{\rm Hom}}_S(\_\_, \omega _S)$
to the short exact sequence of
![]() $S$
-modules
$S$
-modules
we obtain another short exact sequence of
![]() $S$
-modules:
$S$
-modules:
Therefore, we obtain a filtration of
![]() $N=\omega _S$
by the submodules
$N=\omega _S$
by the submodules
![]() $N_j:=\omega _{S_{q+1-j}}$
as in (2.1), where
$N_j:=\omega _{S_{q+1-j}}$
as in (2.1), where
![]() $q+1={{\rm length}}_S(S)={{\rm length}}_S(\omega _S)$
. The composition of the embeddings in (2.3.1) will be denoted by
$q+1={{\rm length}}_S(S)={{\rm length}}_S(\omega _S)$
. The composition of the embeddings in (2.3.1) will be denoted by
![]() $\varsigma :=\varsigma _{q}\circ \dots \circ \varsigma _1 :\omega _{S_1}\hookrightarrow \omega _{S_{q+1}}= \omega _{S}$
.
$\varsigma :=\varsigma _{q}\circ \dots \circ \varsigma _1 :\omega _{S_1}\hookrightarrow \omega _{S_{q+1}}= \omega _{S}$
.
Recall that the socle of a module
![]() $M$
over a local ring
$M$
over a local ring
![]() $(S,\mathfrak{m},k)$
is
$(S,\mathfrak{m},k)$
is
![]() ${\rm Soc}\ M$
is naturally a
${\rm Soc}\ M$
is naturally a
![]() $k$
-vector space and
$k$
-vector space and
![]() $\dim _k{\rm Soc}\, \omega _S=1$
by the definition of the canonical module. In particular,
$\dim _k{\rm Soc}\, \omega _S=1$
by the definition of the canonical module. In particular,
![]() ${\rm Soc}\, \omega _S\simeq k$
, which is the only
${\rm Soc}\, \omega _S\simeq k$
, which is the only
![]() $S$
-submodule of
$S$
-submodule of
![]() $\omega _S$
isomorphic to
$\omega _S$
isomorphic to
![]() $k$
.
$k$
.
Let us recall [Reference Kollár and KovácsKK20, Lemma 3.4], which will be important later:
Lemma 2.4. Using the notation from (2.2) and (2.3), we have that
Remark 2.4.2. Note that this is not simply stating that the modules in (2.4.1) are isomorphic but that they are equal as submodules of
![]() $\omega _{S}$
.
$\omega _{S}$
.
3. Families over Artinian local rings
We will frequently use the following notation.
Notation 3.1. Let
![]() $A$
be a noetherian ring,
$A$
be a noetherian ring,
![]() $(R,\mathfrak{m})$
a noetherian local
$(R,\mathfrak{m})$
a noetherian local
![]() $A$
-algebra,
$A$
-algebra,
![]() $I\subset R$
a nilpotent ideal and
$I\subset R$
a nilpotent ideal and
![]() $(T,\mathfrak{n})\colon \!\!\!= (R/I,\mathfrak{m}/I)$
, with natural morphism
$(T,\mathfrak{n})\colon \!\!\!= (R/I,\mathfrak{m}/I)$
, with natural morphism
![]() $\alpha :R\twoheadrightarrow T$
.
$\alpha :R\twoheadrightarrow T$
.
Definition 3.2.
Let
![]() $A$
be a noetherian ring, and let
$A$
be a noetherian ring, and let
![]() $(T,\mathfrak n)$
be a noetherian local
$(T,\mathfrak n)$
be a noetherian local
![]() $A$
-algebra, with
$A$
-algebra, with
![]() $i\in \mathbb{N}$
fixed. We say that
$i\in \mathbb{N}$
fixed. We say that
![]() $T$
has liftable
$T$
has liftable
![]() $i^{{th}}\!$
local cohomology over
$i^{{th}}\!$
local cohomology over
![]() $A$
if for any noetherian local
$A$
if for any noetherian local
![]() $A$
-algebra
$A$
-algebra
![]() $(R,\mathfrak{m})$
and nilpotent ideal
$(R,\mathfrak{m})$
and nilpotent ideal
![]() $I\subset R$
such that
$I\subset R$
such that
![]() $R/I\simeq T$
, the natural morphism on local cohomology
$R/I\simeq T$
, the natural morphism on local cohomology
is surjective. Finally, if
![]() $T$
has liftable
$T$
has liftable
![]() $i^{{th}}\!$
local cohomology over
$i^{{th}}\!$
local cohomology over
![]() $A$
for every
$A$
for every
![]() $i\in \mathbb{N}$
, then we say that
$i\in \mathbb{N}$
, then we say that
![]() $T$
has liftable local cohomology over
$T$
has liftable local cohomology over
![]() $A$
[Reference Kollár and KovácsKK20].
$A$
[Reference Kollár and KovácsKK20].
We say that
![]() $T$
has liftable
$T$
has liftable
![]() $i^{{th}}\!$
local cohomology, resp. liftable local cohomology, if it has the relevant property over
$i^{{th}}\!$
local cohomology, resp. liftable local cohomology, if it has the relevant property over
![]() $\mathbb{Z}$
.
$\mathbb{Z}$
.
Remark 3.3. Notice that using the above notation, if
![]() $\phi :A^{\prime}\to A$
is a ring homomorphism from another noetherian ring
$\phi :A^{\prime}\to A$
is a ring homomorphism from another noetherian ring
![]() $A^{\prime}$
, then if
$A^{\prime}$
, then if
![]() $T$
has liftable
$T$
has liftable
![]() $i^{{th}}\!$
local cohomology over
$i^{{th}}\!$
local cohomology over
![]() $A^{\prime}$
, then it also has liftable
$A^{\prime}$
, then it also has liftable
![]() $i^{{th}}\!$
local cohomology over
$i^{{th}}\!$
local cohomology over
![]() $A$
. In particular, if
$A$
. In particular, if
![]() $T$
has liftable
$T$
has liftable
![]() $i^{{th}}\!$
local cohomology over
$i^{{th}}\!$
local cohomology over
![]() $\mathbb{Z}$
, then it has liftable
$\mathbb{Z}$
, then it has liftable
![]() $i^{{th}}\!$
local cohomology over any noetherian ring
$i^{{th}}\!$
local cohomology over any noetherian ring
![]() $A$
justifying the above terminology.
$A$
justifying the above terminology.
Furthermore, if
![]() $A=k$
is a field of characteristic
$A=k$
is a field of characteristic
![]() $0$
, then the notions of having liftable
$0$
, then the notions of having liftable
![]() $i^{{th}}\!$
local cohomology over
$i^{{th}}\!$
local cohomology over
![]() $k$
and over
$k$
and over
![]() $\mathbb{Z}$
are equivalent. This follows in one direction by the above and in the other direction by the Cohen structure theorem [StacksProject, Tag 032A].
$\mathbb{Z}$
are equivalent. This follows in one direction by the above and in the other direction by the Cohen structure theorem [StacksProject, Tag 032A].
Definition 3.4.
We extend this definition to schemes: Let
![]() $(X,x)$
be a local scheme over a noetherian ring
$(X,x)$
be a local scheme over a noetherian ring
![]() $A$
. Then we say that
$A$
. Then we say that
![]() $(X,x)$
has liftable
$(X,x)$
has liftable
![]() $i^{{th}}\!$
local cohomology over
$i^{{th}}\!$
local cohomology over
![]() $A$
if
$A$
if
![]() ${\mathscr{O}}_{X,x}$
has liftable
${\mathscr{O}}_{X,x}$
has liftable
![]() $i^{{th}}\!$
local cohomology over
$i^{{th}}\!$
local cohomology over
![]() $A$
. If
$A$
. If
![]() $f:X\to Z$
is a morphism of schemes, then we say that
$f:X\to Z$
is a morphism of schemes, then we say that
![]() $X$
has liftable
$X$
has liftable
![]() $i^{{th}}\!$
local cohomology over
$i^{{th}}\!$
local cohomology over
![]() $Z$
if
$Z$
if
![]() $(X,x)$
has liftable
$(X,x)$
has liftable
![]() $i^{{th}}\!$
local cohomology over
$i^{{th}}\!$
local cohomology over
![]() $A$
for each
$A$
for each
![]() $x\in X$
and for each
$x\in X$
and for each
![]() ${\rm Spec}\, A\subseteq Z$
open affine neighbourhood of
${\rm Spec}\, A\subseteq Z$
open affine neighbourhood of
![]() $f(x)\in Z$
. This also extends the notion of liftable local cohomology in the obvious way.
$f(x)\in Z$
. This also extends the notion of liftable local cohomology in the obvious way.
Lemma 3.5.
Let
![]() $X\to Y\to Z$
be morphisms schemes. If
$X\to Y\to Z$
be morphisms schemes. If
![]() $X$
has liftable
$X$
has liftable
![]() $i^{{th}}\!$
local cohomology over
$i^{{th}}\!$
local cohomology over
![]() $Z$
, then
$Z$
, then
![]() $X$
has liftable
$X$
has liftable
![]() $i^{{th}}\!$
local cohomology over
$i^{{th}}\!$
local cohomology over
![]() $Y$
as well.
$Y$
as well.
In particular, if
![]() $X$
has liftable
$X$
has liftable
![]() $i^{{th}}\!$
local cohomology over a field
$i^{{th}}\!$
local cohomology over a field
![]() $k$
, then it has liftable
$k$
, then it has liftable
![]() $i^{{th}}\!$
local cohomology over any other
$i^{{th}}\!$
local cohomology over any other
![]() $k$
-scheme to which it admits a morphism. In addition if
$k$
-scheme to which it admits a morphism. In addition if
![]() ${\rm char}\, k=0$
, then
${\rm char}\, k=0$
, then
![]() $X$
has liftable
$X$
has liftable
![]() $i^{{th}}\!$
local cohomology.
$i^{{th}}\!$
local cohomology.
Proof. This follows from the definitions and Remark 3.3.
Let us recall the following simple lemma from [Reference Kollár and KovácsKK20, Lemma 4.4]:
Lemma 3.6.
Using Notation 3.1
, let
![]() $M$
be an
$M$
be an
![]() $R$
-module such that there exists a surjective
$R$
-module such that there exists a surjective
![]() $R$
-module homomorphism
$R$
-module homomorphism
![]() $\phi : M\twoheadrightarrow T$
. Assume that the induced natural homomorphism
$\phi : M\twoheadrightarrow T$
. Assume that the induced natural homomorphism
![]() $H^i_{\mathfrak{m}}(R) \twoheadrightarrow H^i_{\mathfrak{n}}(T)$
is surjective for some
$H^i_{\mathfrak{m}}(R) \twoheadrightarrow H^i_{\mathfrak{n}}(T)$
is surjective for some
![]() $i\in \mathbb{N}$
. Then the induced homomorphism on local cohomology
$i\in \mathbb{N}$
. Then the induced homomorphism on local cohomology
is surjective for the same
![]() $i$
. In particular, if
$i$
. In particular, if
![]() $(T,\mathfrak{n})$
has liftable local cohomology over
$(T,\mathfrak{n})$
has liftable local cohomology over
![]() $A$
, then the homomorphism in (3.1) is surjective for every
$A$
, then the homomorphism in (3.1) is surjective for every
![]() $i\in \mathbb{N}$
.
$i\in \mathbb{N}$
.
We will also need the following.
Lemma 3.7.
Let
![]() $\mathcal{D}_i$
be the derived category of an abelian category
$\mathcal{D}_i$
be the derived category of an abelian category
![]() $\mathcal{A}_i$
for
$\mathcal{A}_i$
for
![]() $i=1,2$
and
$i=1,2$
and
![]() $\Phi :\mathcal{D}_1\to \mathcal{D}_2$
a triangulated functor, and define
$\Phi :\mathcal{D}_1\to \mathcal{D}_2$
a triangulated functor, and define
![]() $\Phi ^i\colon \!\!\!= h^i\circ \Phi :\mathcal{D}_1\to \mathcal{A}_2$
. Let
$\Phi ^i\colon \!\!\!= h^i\circ \Phi :\mathcal{D}_1\to \mathcal{A}_2$
. Let
![]() $\textsf{A}\in {\rm Ob}\,\mathcal{D}_1$
such that
$\textsf{A}\in {\rm Ob}\,\mathcal{D}_1$
such that
![]() $h^j(\textsf{A})=0$
for
$h^j(\textsf{A})=0$
for
![]() $j\gt d$
for some
$j\gt d$
for some
![]() $d\in \mathbb{Z}$
, and assume that there exists an
$d\in \mathbb{Z}$
, and assume that there exists an
![]() $m\in \mathbb{N}$
such that
$m\in \mathbb{N}$
such that
![]() $\Phi ^i(h^j(\textsf{A}))=0$
for
$\Phi ^i(h^j(\textsf{A}))=0$
for
![]() $i\gt m$
and for each
$i\gt m$
and for each
![]() $j\in \mathbb{Z}$
. Then
$j\in \mathbb{Z}$
. Then
![]() $\Phi ^i(\textsf{A})=0$
for
$\Phi ^i(\textsf{A})=0$
for
![]() $i\gt m+d$
.
$i\gt m+d$
.
Proof.
Consider the conjugate spectral sequence associated to
![]() $\textsf{A}$
and
$\textsf{A}$
and
![]() $\Phi$
:
$\Phi$
:
By the assumptions,
![]() $E^{p,q}_2=0$
if either
$E^{p,q}_2=0$
if either
![]() $p\gt m$
or
$p\gt m$
or
![]() $q\gt d$
, which implies that
$q\gt d$
, which implies that
![]() $E^{p,q}_2=0$
for
$E^{p,q}_2=0$
for
![]() $p+q\gt m+d$
. This implies the desired statement.
$p+q\gt m+d$
. This implies the desired statement.
Definition 3.8.
Let
![]() $f:X\to Y$
be a morphism. Then
$f:X\to Y$
be a morphism. Then
![]() $f$
is said to be flat in codimension
$f$
is said to be flat in codimension
![]() $t$
if there exists a closed subset
$t$
if there exists a closed subset
![]() $Z\subseteq X$
such that
$Z\subseteq X$
such that
![]() ${\rm codim}(Z\cap X_y,X_y)\geq t+1$
for every
${\rm codim}(Z\cap X_y,X_y)\geq t+1$
for every
![]() $y\in Y$
and
$y\in Y$
and
![]() $f\vert _{X\setminus Z}$
is flat.
$f\vert _{X\setminus Z}$
is flat.
In the proof of the next statement, we will use the canonical truncation of cochain complexes of objects of an abelian category, which has the property that its cohomology objects are the same as the original complex up to or above the given index. We follow the notation and terminology of [StacksProject, Tag 0118]. In particular, for any complex
![]() ${C}^{\small{\bullet}}$
and any
${C}^{\small{\bullet}}$
and any
![]() $r\in \mathbb{Z}$
, we have the following distinguished triangle of complexes,
$r\in \mathbb{Z}$
, we have the following distinguished triangle of complexes,
Corollary 3.9.
Let
![]() $(S,\mathfrak{m},k)$
be an Artinian local ring,
$(S,\mathfrak{m},k)$
be an Artinian local ring,
![]() $N$
a finite
$N$
a finite
![]() $S$
-module,
$S$
-module,
![]() $(X,x)$
a local scheme of dimension
$(X,x)$
a local scheme of dimension
![]() $n$
and
$n$
and
![]() $f:(X,x)\to ({\rm Spec}\, S,\mathfrak{m})$
a local morphism. Assume that
$f:(X,x)\to ({\rm Spec}\, S,\mathfrak{m})$
a local morphism. Assume that
![]() $f$
is flat in codimension
$f$
is flat in codimension
![]() $t-1$
. Then the natural morphism
$t-1$
. Then the natural morphism
is an isomorphism for
![]() $i\geq n-t$
.
$i\geq n-t$
.
Proof.
As
![]() $f$
is flat in codimension
$f$
is flat in codimension
![]() $t-1$
, it follows that
$t-1$
, it follows that
![]() $\dim {\rm supp}\,{\mathcal{L}}^jf^*N\leq n-t$
for each
$\dim {\rm supp}\,{\mathcal{L}}^jf^*N\leq n-t$
for each
![]() $j\lt 0$
. This implies that
$j\lt 0$
. This implies that
![]() $H^i_x({\mathcal{L}}^jf^*N)=0$
for
$H^i_x({\mathcal{L}}^jf^*N)=0$
for
![]() $i\gt n-t$
and
$i\gt n-t$
and
![]() $j\lt 0$
. Let
$j\lt 0$
. Let
![]() $\textsf{A}\colon \!\!\!= \tau _{\leq -1}({\mathcal{L}} f^*N)$
and
$\textsf{A}\colon \!\!\!= \tau _{\leq -1}({\mathcal{L}} f^*N)$
and
![]() $\textsf{B}\colon \!\!\!= \tau _{\geq 0}({\mathcal{L}} f^*N)$
. Then (3.8.1) gives a distinguished triangle of complexes of
$\textsf{B}\colon \!\!\!= \tau _{\geq 0}({\mathcal{L}} f^*N)$
. Then (3.8.1) gives a distinguished triangle of complexes of
![]() ${\mathscr{O}}_X$
-modules,
${\mathscr{O}}_X$
-modules,
Furthermore,
![]() $h^{j}(\textsf{A})={\mathcal{L}}^{j}f^*N$
for
$h^{j}(\textsf{A})={\mathcal{L}}^{j}f^*N$
for
![]() $j\lt 0$
and
$j\lt 0$
and
![]() $h^{j}(\textsf{A})=0$
for
$h^{j}(\textsf{A})=0$
for
![]() $j\geq 0$
; hence Lemma 3.7 (for
$j\geq 0$
; hence Lemma 3.7 (for
![]() $\textsf{A}$
,
$\textsf{A}$
,
![]() $\Phi ={\mathcal{R}}\Gamma _x$
,
$\Phi ={\mathcal{R}}\Gamma _x$
,
![]() $m=n-t$
and
$m=n-t$
and
![]() $d=-1$
) implies that
$d=-1$
) implies that
![]() ${\mathcal{R}}^{\,i}\Gamma _x(\textsf{A})=0$
for
${\mathcal{R}}^{\,i}\Gamma _x(\textsf{A})=0$
for
![]() $i\gt n-t-1$
. Finally,
$i\gt n-t-1$
. Finally,
![]() $\textsf{B}\,{\simeq }_{{\rm qis}}\, f^*N$
, so the desired statement follows.
$\textsf{B}\,{\simeq }_{{\rm qis}}\, f^*N$
, so the desired statement follows.
Proposition 3.10.
Let
![]() $(S,\mathfrak{m},k)$
be an Artinian local ring,
$(S,\mathfrak{m},k)$
be an Artinian local ring,
![]() $(X,x)$
a local scheme of dimension
$(X,x)$
a local scheme of dimension
![]() $n$
and
$n$
and
![]() $f:(X,x)\to ({\rm Spec}\, S,\mathfrak{m})$
a local morphism. Assume that
$f:(X,x)\to ({\rm Spec}\, S,\mathfrak{m})$
a local morphism. Assume that
![]() $f$
is flat in codimension
$f$
is flat in codimension
![]() $t-1$
. Let
$t-1$
. Let
![]() $N$
be a finite
$N$
be a finite
![]() $S$
-module with a filtration as in (2.1), and assume that
$S$
-module with a filtration as in (2.1), and assume that
![]() $(X_{k}, x)$
, where
$(X_{k}, x)$
, where
![]() $X_{k}$
is the fiber of
$X_{k}$
is the fiber of
![]() $f$
over the closed point of
$f$
over the closed point of
![]() ${\rm Spec}\, S$
and has liftable
${\rm Spec}\, S$
and has liftable
![]() $i^{{th}}\!$
local cohomology for
$i^{{th}}\!$
local cohomology for
![]() $i\geq n-t$
over
$i\geq n-t$
over
![]() $S$
. Then for each
$S$
. Then for each
![]() $i\gt n-t$
and for each
$i\gt n-t$
and for each
![]() $j$
, the natural sequence of morphisms induced by the embeddings
$j$
, the natural sequence of morphisms induced by the embeddings
![]() $N_{j+1}\hookrightarrow N_j$
forms a short exact sequence,
$N_{j+1}\hookrightarrow N_j$
forms a short exact sequence,
Proof.
Because
![]() $\mathcal{ann}\left ({N_{j}}\Big /{N_{j+1}}\right ) =\mathfrak{m}$
, there is a natural surjective morphism
$\mathcal{ann}\left ({N_{j}}\Big /{N_{j+1}}\right ) =\mathfrak{m}$
, there is a natural surjective morphism
By Lemma 3.6 and (2.1.1), the natural homomorphism
is surjective for all
![]() $i\geq n-t$
. Next, consider the distinguished triangle
$i\geq n-t$
. Next, consider the distinguished triangle
and the induced long exact cohomology sequence for the functor
![]() ${\mathcal{R}}\Gamma _x$
. By Corollary 3.9 the terms of that long exact sequence may be replaced by terms in the form of
${\mathcal{R}}\Gamma _x$
. By Corollary 3.9 the terms of that long exact sequence may be replaced by terms in the form of
![]() $H^i_x(f^*(\ \ ))$
for
$H^i_x(f^*(\ \ ))$
for
![]() $i\geq n-t$
, and hence the statement follows from (3.10.1).
$i\geq n-t$
, and hence the statement follows from (3.10.1).
3.11. The exceptional inverse image of the structure sheaves.Let
![]() $(S,\mathfrak{m},k)$
be an Artinian local ring with a filtration by ideals as in (2.2). Further, let
$(S,\mathfrak{m},k)$
be an Artinian local ring with a filtration by ideals as in (2.2). Further, let
![]() $f:X\to {\rm Spec}\, S$
be a morphism that is essentially of finite type and
$f:X\to {\rm Spec}\, S$
be a morphism that is essentially of finite type and
![]() $f_j=f\vert _{X_j}:X_j:=X\times _{{\rm Spec}\, S}{\rm Spec}\, S_j\to {\rm Spec}\, S_j$
, where
$f_j=f\vert _{X_j}:X_j:=X\times _{{\rm Spec}\, S}{\rm Spec}\, S_j\to {\rm Spec}\, S_j$
, where
![]() $S_j=S/I_j$
as defined in (2.2), e.g.,
$S_j=S/I_j$
as defined in (2.2), e.g.,
![]() $X_{q+1}=X$
and
$X_{q+1}=X$
and
![]() $X_{1}=X_{k}$
, the fiber of
$X_{1}=X_{k}$
, the fiber of
![]() $f$
over the closed point of
$f$
over the closed point of
![]() $S$
. By a slight abuse of notation, we will denote
$S$
. By a slight abuse of notation, we will denote
![]() $\omega _{{\rm Spec}\, S}$
with
$\omega _{{\rm Spec}\, S}$
with
![]() $\omega _S$
as well, but it will be clear from the context which one is meant at any given time.
$\omega _S$
as well, but it will be clear from the context which one is meant at any given time.
Using the description of the exceptional inverse image functor via the residual/dualizing complexes [Reference ConradCon00, (3.3.6)] (cf. [Reference HartshorneR&D66, 3.4(a)], [StacksProject, Tag 0E9L]):
and because
![]() $S$
is Artinian,
$S$
is Artinian,
![]() ${\omega }^{\small{\bullet}}_{S_j}\simeq \omega _{S_j}$
for each
${\omega }^{\small{\bullet}}_{S_j}\simeq \omega _{S_j}$
for each
![]() $j$
, and we have that
$j$
, and we have that
In the rest of this section, we will use the following notation and assumptions.
Assumption 3.12.
Let
![]() $(S,\mathfrak{m},k)$
be an Artinian local ring,
$(S,\mathfrak{m},k)$
be an Artinian local ring,
![]() $(X,x)$
a local scheme of dimension
$(X,x)$
a local scheme of dimension
![]() $n$
and
$n$
and
![]() $f:(X,x)\to ({\rm Spec}\, S,\mathfrak{m})$
a local morphism. Assume that
$f:(X,x)\to ({\rm Spec}\, S,\mathfrak{m})$
a local morphism. Assume that
![]() $f$
is flat in codimension
$f$
is flat in codimension
![]() $t-1$
and that
$t-1$
and that
![]() $(X_{k}, x)$
, where
$(X_{k}, x)$
, where
![]() $X_{k}$
is the fiber of
$X_{k}$
is the fiber of
![]() $f$
over the closed point of
$f$
over the closed point of
![]() ${\rm Spec}\, S$
and has liftable
${\rm Spec}\, S$
and has liftable
![]() $i^{{th}}\!$
local cohomology for
$i^{{th}}\!$
local cohomology for
![]() $i\geq n-t$
over
$i\geq n-t$
over
![]() $S$
.
$S$
.
Theorem 3.13.
For each
![]() $i\gt n-t$
and each
$i\gt n-t$
and each
![]() $j\in \mathbb{N}$
,
$j\in \mathbb{N}$
,
-
(i) there exists a natural surjective morphism
 $ \varrho _{i,j} : \textsf{h}^{-i}({\omega }^{\small{\bullet}} _{X_{j+1}/S_{j+1}})\twoheadrightarrow \textsf{h}^{-i}({\omega }^{\small{\bullet}} _{X_{j}/S_{j}})$
,
$ \varrho _{i,j} : \textsf{h}^{-i}({\omega }^{\small{\bullet}} _{X_{j+1}/S_{j+1}})\twoheadrightarrow \textsf{h}^{-i}({\omega }^{\small{\bullet}} _{X_{j}/S_{j}})$
, -
(ii) there exists a natural surjective morphism
 $ \varrho ^i= \varrho _{i,1}\circ \dots \circ \varrho _{i,q} : \textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})\twoheadrightarrow \textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X_{k}})$
$ \varrho ^i= \varrho _{i,1}\circ \dots \circ \varrho _{i,q} : \textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})\twoheadrightarrow \textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X_{k}})$
-
(iii) the natural morphisms
 $\varrho _{i,j}$
fit into a short exact sequence,
$\varrho _{i,j}$
fit into a short exact sequence,
 \begin{align*} 0 \longrightarrow \textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X_{k}}) \longrightarrow \textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X_{j+1}/S_{j+1}}) \stackrel {\varrho _{i,j}}\longrightarrow \textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X_j/S_j}) \longrightarrow 0, \end{align*}
\begin{align*} 0 \longrightarrow \textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X_{k}}) \longrightarrow \textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X_{j+1}/S_{j+1}}) \stackrel {\varrho _{i,j}}\longrightarrow \textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X_j/S_j}) \longrightarrow 0, \end{align*}
-
(iv)
 $\ker \varrho _{i,j} = I_{j}\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X_{j+1}/S_{j+1}}) \simeq{I_{j}\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})}\Big /{I_{j+1}\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})}$
,
$\ker \varrho _{i,j} = I_{j}\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X_{j+1}/S_{j+1}}) \simeq{I_{j}\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})}\Big /{I_{j+1}\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})}$
, -
(v)
 $\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X_{j}/S_{j}})\simeq{\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})} \Big /{I_{j}\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})}\simeq{\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})} \otimes _{{\mathscr{O}}_X}{\mathscr{O}}_{X_j}$
and
$\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X_{j}/S_{j}})\simeq{\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})} \Big /{I_{j}\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})}\simeq{\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})} \otimes _{{\mathscr{O}}_X}{\mathscr{O}}_{X_j}$
and
-
(vi)
 $\ker \varrho ^i = \mathfrak{m}\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})$
.
$\ker \varrho ^i = \mathfrak{m}\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})$
.
Proof.
Let
![]() $N=\omega _S$
and consider the filtration on
$N=\omega _S$
and consider the filtration on
![]() $N$
given by
$N$
given by
![]() $N_{j}=\omega _{S_{q+1-j}}$
, cf. (2.3), (2.3.1). Further, let
$N_{j}=\omega _{S_{q+1-j}}$
, cf. (2.3), (2.3.1). Further, let
![]() $(\ )\widehat{\ }$
denote the completion at
$(\ )\widehat{\ }$
denote the completion at
![]() $x$
(the closed point of
$x$
(the closed point of
![]() $X$
). Then by Proposition 3.10, for each
$X$
). Then by Proposition 3.10, for each
![]() $i\gt n-t$
and each
$i\gt n-t$
and each
![]() $j$
, there exists a short exact sequence
$j$
, there exists a short exact sequence
Notice that
![]() $f^*\omega _{S_j}\simeq f_j^*\omega _{S_j}$
. Combining this observation for both
$f^*\omega _{S_j}\simeq f_j^*\omega _{S_j}$
. Combining this observation for both
![]() $j$
and
$j$
and
![]() $j+1$
with Corollary 3.9 yields that this short exact sequence may also be written as
$j+1$
with Corollary 3.9 yields that this short exact sequence may also be written as
Applying local duality [StacksProject, Tag 0AAK] to (3.13.2) gives the short exact sequence
Since completion is faithfully flat [StacksProject, Tag 00MC], this implies that there are short exact sequences

By Grothendieck duality
and hence
![]() ${\mathcal{Ext}}^{-i}_{X}\left ({\mathcal{L}} f_j^*\omega _{S_{j}},{\omega }^{\small{\bullet}}_{X} \right )\simeq \textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X_{j}/S_{j}})$
for each
${\mathcal{Ext}}^{-i}_{X}\left ({\mathcal{L}} f_j^*\omega _{S_{j}},{\omega }^{\small{\bullet}}_{X} \right )\simeq \textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X_{j}/S_{j}})$
for each
![]() $i,j$
, by (3.11.2). Therefore, defining
$i,j$
, by (3.11.2). Therefore, defining
![]() $\varrho _{i,j}$
as the surjective morphism in (3.13.3) implies (i). Composing the surjective morphisms in (3.13.1) for all
$\varrho _{i,j}$
as the surjective morphism in (3.13.3) implies (i). Composing the surjective morphisms in (3.13.1) for all
![]() $j$
implies that the natural morphism
$j$
implies that the natural morphism
is surjective, and hence (ii) follows as well.
By (2.3.1)
![]() $f^*\left ({\omega _{S_{j+1}}}\Big /{\omega _{S_{j}}}\right )\simeq{\mathscr{O}}_{X_{k}}$
, and hence
$f^*\left ({\omega _{S_{j+1}}}\Big /{\omega _{S_{j}}}\right )\simeq{\mathscr{O}}_{X_{k}}$
, and hence
![]() ${\mathcal{Ext}}^{-i}_{X} \left (f^*\left ({\omega _{S_{j+1}}}\Big /{\omega _{S_{j}}}\right ),{\omega }^{\small{\bullet}}_{X} \right )\simeq \textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X_{k}})$
, (3.13.3) also implies (iii).
${\mathcal{Ext}}^{-i}_{X} \left (f^*\left ({\omega _{S_{j+1}}}\Big /{\omega _{S_{j}}}\right ),{\omega }^{\small{\bullet}}_{X} \right )\simeq \textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X_{k}})$
, (3.13.3) also implies (iii).
Composing the injective maps in (3.13.1) for all
![]() $j$
shows that the embedding
$j$
shows that the embedding
![]() $\varsigma : \omega _{S_1}\hookrightarrow \omega _S$
induces an embedding on local cohomology:
$\varsigma : \omega _{S_1}\hookrightarrow \omega _S$
induces an embedding on local cohomology:
Next we prove (iv) for
![]() $j=q$
first. Because
$j=q$
first. Because
![]() $\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X_{q}/S_{q}})$
is supported on
$\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X_{q}/S_{q}})$
is supported on
![]() $X_{q}$
, it follows that
$X_{q}$
, it follows that
Recall from (2.2) that there exists a
![]() $t_{q}\in I_{q}$
such that
$t_{q}\in I_{q}$
such that
![]() $I_{q}=St_{q}\simeq S\Big /\mathfrak{m}$
and from Lemma 2.4 that
$I_{q}=St_{q}\simeq S\Big /\mathfrak{m}$
and from Lemma 2.4 that
![]() $I_{q}\omega _S={\rm Soc}\, \omega _S$
. It follows that for
$I_{q}\omega _S={\rm Soc}\, \omega _S$
. It follows that for
![]() $j=q$
, the short exact sequence of (2.3.1) takes the form
$j=q$
, the short exact sequence of (2.3.1) takes the form
where
![]() $\tau :\omega _S\twoheadrightarrow {\rm Soc}\, \omega _S\subset \omega _S$
may be identified with multiplication by
$\tau :\omega _S\twoheadrightarrow {\rm Soc}\, \omega _S\subset \omega _S$
may be identified with multiplication by
![]() $t_{q}$
on
$t_{q}$
on
![]() $\omega _S$
. Applying
$\omega _S$
. Applying
![]() $f^*$
and taking local cohomology, we obtain the sequence
$f^*$
and taking local cohomology, we obtain the sequence
which coincides with (3.13.1) for
![]() $j=q$
, and hence it is exact. Further note that the morphism
$j=q$
, and hence it is exact. Further note that the morphism
![]() $H^i_x(\tau )$
may also be identified with multiplication by
$H^i_x(\tau )$
may also be identified with multiplication by
![]() $t_{q}$
on
$t_{q}$
on
![]() $H^i_x(f^*\omega _S)$
. By Lemma 2.4 and (3.13.4), the natural morphism
$H^i_x(f^*\omega _S)$
. By Lemma 2.4 and (3.13.4), the natural morphism
![]() $H^i_x(\varsigma ): H^i_x\left (f^*{\rm Soc}\, \omega _S \right ) =H^i_x(I_qf^*\omega _S) = H^i_x(f^*\omega _{S_1}) \to H^i_x(f^*\omega _S)$
is injective. Because
$H^i_x(\varsigma ): H^i_x\left (f^*{\rm Soc}\, \omega _S \right ) =H^i_x(I_qf^*\omega _S) = H^i_x(f^*\omega _{S_1}) \to H^i_x(f^*\omega _S)$
is injective. Because
![]() $H^i_x(\tau )$
, i.e., multiplication by
$H^i_x(\tau )$
, i.e., multiplication by
![]() $t_q$
on
$t_q$
on
![]() $H^i_x(f^*\omega _{S})$
, is surjective onto
$H^i_x(f^*\omega _{S})$
, is surjective onto
![]() $H^i_x\left (f^*{\rm Soc}\, \omega _S \right )$
, it follows that
$H^i_x\left (f^*{\rm Soc}\, \omega _S \right )$
, it follows that

i.e.,
![]() $H^i_x\left (f^*{\rm Soc}\, \omega _S \right )$
coincides with
$H^i_x\left (f^*{\rm Soc}\, \omega _S \right )$
coincides with
![]() $I_{q} H^i_x(f^*\omega _{S})$
as submodules of
$I_{q} H^i_x(f^*\omega _{S})$
as submodules of
![]() $H^i_x(f^*\omega _{S})$
. Next let
$H^i_x(f^*\omega _{S})$
. Next let
![]() $E$
be an injective hull of
$E$
be an injective hull of
![]() $\kappa (x)={{\mathscr{O}}_{X,x}}\Big /{\mathfrak{m}_{X,x}}$
, and consider a morphism
$\kappa (x)={{\mathscr{O}}_{X,x}}\Big /{\mathfrak{m}_{X,x}}$
, and consider a morphism
![]() $\phi : H^i_x(f^*{\rm Soc}\, \omega _S)\to E$
. As
$\phi : H^i_x(f^*{\rm Soc}\, \omega _S)\to E$
. As
![]() $E$
is injective,
$E$
is injective,
![]() $\phi$
extends to a morphism
$\phi$
extends to a morphism
![]() $\widetilde \phi : H^i_x(f^*\omega _S)\to E$
. If
$\widetilde \phi : H^i_x(f^*\omega _S)\to E$
. If
![]() $a\in H^i_x(f^*\omega _S)$
, then
$a\in H^i_x(f^*\omega _S)$
, then
![]() $t_{q}a\in I_{q}H^i_x(f^*\omega _S)=H^i_x\left (f^*{\rm Soc}\, \omega _S \right )$
, so
$t_{q}a\in I_{q}H^i_x(f^*\omega _S)=H^i_x\left (f^*{\rm Soc}\, \omega _S \right )$
, so
Therefore,
![]() $\phi \circ H^i_x(\tau )= t_{q}\widetilde \phi$
. Similarly, if
$\phi \circ H^i_x(\tau )= t_{q}\widetilde \phi$
. Similarly, if
![]() $\psi : H^i_x(f^*\omega _S)\to E$
is an arbitrary morphism, then setting
$\psi : H^i_x(f^*\omega _S)\to E$
is an arbitrary morphism, then setting
![]() $\phi =\psi \vert _{H^i_x(f^*{\rm Soc}\, \omega _S)}: H^i_x(f^*{\rm Soc}\, \omega _S)\to E$
and applying the same computation as above, with
$\phi =\psi \vert _{H^i_x(f^*{\rm Soc}\, \omega _S)}: H^i_x(f^*{\rm Soc}\, \omega _S)\to E$
and applying the same computation as above, with
![]() $\widetilde \phi$
replaced by
$\widetilde \phi$
replaced by
![]() $\psi$
, shows that
$\psi$
, shows that
![]() $\phi \circ H^i_x(\tau )= t_{q}\psi$
. It follows that the embedding induced by
$\phi \circ H^i_x(\tau )= t_{q}\psi$
. It follows that the embedding induced by
![]() $H^i_x(\tau )$
,
$H^i_x(\tau )$
,
identifies
![]() ${{\rm Hom}}_X(H^i_x(f^*{\rm Soc}\, \omega _S), E)$
, with
${{\rm Hom}}_X(H^i_x(f^*{\rm Soc}\, \omega _S), E)$
, with
![]() $I_{q}{{\rm Hom}}_X(H^i_x(f^*\omega _S), E)$
. By local duality it follows that
$I_{q}{{\rm Hom}}_X(H^i_x(f^*\omega _S), E)$
. By local duality it follows that
and hence, because completion is faithfully flat, this implies (iv) in the case
![]() $j=q$
. Running through the same argument with
$j=q$
. Running through the same argument with
![]() $S$
replaced by
$S$
replaced by
![]() $S_{j+1}$
gives the equality in (iv) for all
$S_{j+1}$
gives the equality in (iv) for all
![]() $j$
. In addition, (iv) for
$j$
. In addition, (iv) for
![]() $j=q$
implies (v) for
$j=q$
implies (v) for
![]() $j\geq q$
. Assuming that (v) holds for
$j\geq q$
. Assuming that (v) holds for
![]() $j=r+1$
implies the isomorphism in (vi) for
$j=r+1$
implies the isomorphism in (vi) for
![]() $j=r$
. In turn, the entire (iv) for
$j=r$
. In turn, the entire (iv) for
![]() $j=r$
, combined with (v) for
$j=r$
, combined with (v) for
![]() $j=r+1$
, implies (v) for
$j=r+1$
, implies (v) for
![]() $j=r$
. Therefore, (iv) and (v) follow by descending induction on
$j=r$
. Therefore, (iv) and (v) follow by descending induction on
![]() $j$
, and then (vi) follows from (iv) and the definition of
$j$
, and then (vi) follows from (iv) and the definition of
![]() $\varrho ^i$
.
$\varrho ^i$
.
We will also need the following simple lemma from [Reference Kollár and KovácsKK20, 4.11].
Lemma 3.14.
Let
![]() $R$
be a ring,
$R$
be a ring,
![]() $M$
an
$M$
an
![]() $R$
-module,
$R$
-module,
![]() $t\in R$
and
$t\in R$
and
![]() $J=(t)\subseteq R$
. Assume that
$J=(t)\subseteq R$
. Assume that
![]() $(0:J)_M=(0:J)_R\cdot M$
. Then the natural morphism
$(0:J)_M=(0:J)_R\cdot M$
. Then the natural morphism
![]() $J\otimes _R M \stackrel{\simeq }\longrightarrow JM$
is an isomorphism.
$J\otimes _R M \stackrel{\simeq }\longrightarrow JM$
is an isomorphism.
The the following proposition and its proof are essentially the same as that of [Reference Kollár and KovácsKK20, Prop. 4.12]. We include it here because the original situation here is slightly different than [Reference Kollár and KovácsKK20], although the difference in the original situation does not influence anything in this particular proof.
Proposition 3.15. Using the same notation as above,
-
(i)
 $I_j\otimes \textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})\simeq I_{j}\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})$
,
$I_j\otimes \textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})\simeq I_{j}\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})$
, -
(ii) for any
 $l\in \mathbb{N}$
,
$l\in \mathbb{N}$
,
 ${I_j}\Big /{I_{j+l}}\otimes \textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})\simeq{I_{j}\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})}\Big /{I_{j+l}\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})}$
, and
${I_j}\Big /{I_{j+l}}\otimes \textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})\simeq{I_{j}\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})}\Big /{I_{j+l}\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})}$
, and
-
(iii) for any
 $l\in \mathbb{N}$
,
$l\in \mathbb{N}$
,
 ${\mathfrak{m}^l}\Big /{\mathfrak{m}^{l+1}}\otimes \textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})\simeq{\mathfrak{m}^l\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})}\Big /{\mathfrak{m}^{l+1}\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})}$
.
${\mathfrak{m}^l}\Big /{\mathfrak{m}^{l+1}}\otimes \textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})\simeq{\mathfrak{m}^l\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})}\Big /{\mathfrak{m}^{l+1}\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})}$
.
Proof.
Notice that since
![]() $H^i_x(f^*{\rm Soc}\, \omega _S)$
is both a quotient and a submodule of
$H^i_x(f^*{\rm Soc}\, \omega _S)$
is both a quotient and a submodule of
![]() $H^i_x(f^*\omega _S)$
, there are two natural maps between
$H^i_x(f^*\omega _S)$
, there are two natural maps between
![]() ${{\rm Hom}}_{{\mathscr{O}}_{X,x}}(H^i_x(f^*{\rm Soc}\, \omega _S), E)$
and
${{\rm Hom}}_{{\mathscr{O}}_{X,x}}(H^i_x(f^*{\rm Soc}\, \omega _S), E)$
and
![]() ${{\rm Hom}}_{{\mathscr{O}}_{X,x}}( H^i_x(f^*\omega _S), E)$
. Regarding
${{\rm Hom}}_{{\mathscr{O}}_{X,x}}( H^i_x(f^*\omega _S), E)$
. Regarding
![]() $H^i_x(f^*{\rm Soc}\, \omega _S)$
as a quotient module via
$H^i_x(f^*{\rm Soc}\, \omega _S)$
as a quotient module via
![]() $H^i_x(\tau )$
, we get the embedding
$H^i_x(\tau )$
, we get the embedding
![]() $\alpha =(\_\_)\circ H^i_x(\tau )$
in (3.13.8) and consider it a submodule on the restriction map
$\alpha =(\_\_)\circ H^i_x(\tau )$
in (3.13.8) and consider it a submodule on the restriction map

These maps are of course not inverses to each other. In fact, we have already established (cf. (3.13.8)) that
![]() $\phi \vert _{H^i_x(f^*{\rm Soc}\, \omega _S)}\circ H^i_x(\tau )= t_{q}\phi$
, and hence the composition
$\phi \vert _{H^i_x(f^*{\rm Soc}\, \omega _S)}\circ H^i_x(\tau )= t_{q}\phi$
, and hence the composition
![]() $\alpha \circ \beta$
is simply multiplication by
$\alpha \circ \beta$
is simply multiplication by
![]() $t_q$
:
$t_q$
:

This implies, (cf. (3.13.4) and (3.13.7)), that
![]() $\varrho ^i$
may be identified with multiplication by
$\varrho ^i$
may be identified with multiplication by
![]() $t_q$
on
$t_q$
on
![]() $\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})$
. Together with Theorem 3.12(vi) this implies that
$\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})$
. Together with Theorem 3.12(vi) this implies that
and hence the natural morphism. The exceptional inverse image of the structure sheaves
is an isomorphism by Lemma 3.14. Now assume, by induction, that (i) holds for
![]() $S_q$
in place of
$S_q$
in place of
![]() $S$
. In particular, keeping in mind that
$S$
. In particular, keeping in mind that
![]() $S_q= S\Big /{I_q}$
, the natural map
$S_q= S\Big /{I_q}$
, the natural map
is an isomorphism for all
![]() $j$
. Consider the short exact sequence (cf. Theorem 3.13(v)),
$j$
. Consider the short exact sequence (cf. Theorem 3.13(v)),
and apply
![]() ${I_{j}}\Big /{I_{q}}\otimes _{S} (\_\_)$
. The image of
${I_{j}}\Big /{I_{q}}\otimes _{S} (\_\_)$
. The image of
![]() ${I_{j}}\Big /{I_{q}}\otimes _{S} I_q \textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})$
in
${I_{j}}\Big /{I_{q}}\otimes _{S} I_q \textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})$
in
![]() ${I_{j}}\Big /{I_{q}}\otimes _{S} \textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})$
is
${I_{j}}\Big /{I_{q}}\otimes _{S} \textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})$
is
![]() $0$
and hence by (3.15.3),the natural map
$0$
and hence by (3.15.3),the natural map

is an isomorphism. This, combined with (3.15.2) and the 5-lemma, implies (i). Then (ii) is a direct consequence of (i) and the fact that tensor product is right exact.
Finally, recall, that the choice of filtration in (2.2) was fairly unrestricted. In particular, we may assume that the filtration
![]() $I_\cdot$
of
$I_\cdot$
of
![]() $S$
is chosen so that for all
$S$
is chosen so that for all
![]() $l\in \mathbb{N}$
, there exists a
$l\in \mathbb{N}$
, there exists a
![]() $j(l)$
such that
$j(l)$
such that
![]() $I_{j(l)}=\mathfrak{m}^l$
. Applying (ii) for this filtration implies (iii).
$I_{j(l)}=\mathfrak{m}^l$
. Applying (ii) for this filtration implies (iii).
The following theorem is an easy combination of the results of this section.
Theorem 3.16.
Let
![]() $(S,\mathfrak{m},k)$
be an Artinian local ring,
$(S,\mathfrak{m},k)$
be an Artinian local ring,
![]() $(X,x)$
a local scheme of dimension
$(X,x)$
a local scheme of dimension
![]() $n$
, and
$n$
, and
![]() $f:(X,x)\to ({\rm Spec}\, S,\mathfrak{m})$
a local morphism. Assume that
$f:(X,x)\to ({\rm Spec}\, S,\mathfrak{m})$
a local morphism. Assume that
![]() $f$
is flat in codimension
$f$
is flat in codimension
![]() $t-1$
and that
$t-1$
and that
![]() $(X_{k}, x)$
, where
$(X_{k}, x)$
, where
![]() $X_{k}$
is the fiber of
$X_{k}$
is the fiber of
![]() $f$
over the closed point of
$f$
over the closed point of
![]() ${\rm Spec}\, S$
, has liftable
${\rm Spec}\, S$
, has liftable
![]() $i^{{th}}\!$
local cohomology for
$i^{{th}}\!$
local cohomology for
![]() $i\geq n-t$
over
$i\geq n-t$
over
![]() $S$
. Then for each
$S$
. Then for each
![]() $i\gt n-t$
,
$i\gt n-t$
,
![]() $\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})$
is flat over
$\textsf{h}^{-i}({\omega }^{\small{\bullet}}_{X/S})$
is flat over
![]() ${\rm Spec}\, S$
. In particular, if
${\rm Spec}\, S$
. In particular, if
![]() $t\gt 0$
, then
$t\gt 0$
, then
![]() $\omega _{X/S}$
is flat over
$\omega _{X/S}$
is flat over
![]() ${\rm Spec}\, S$
and commutes with arbitrary base change.
${\rm Spec}\, S$
and commutes with arbitrary base change.
Proof.
Flatness follows from Proposition 3.15(iii) and [StacksProject, Tag 0AS8]. If
![]() $t\gt 0$
, then this implies that
$t\gt 0$
, then this implies that
![]() $\omega _{X/S}$
is flat over
$\omega _{X/S}$
is flat over
![]() ${\rm Spec}\, S$
. Furthermore, it commutes with arbitrary base change by Theorem 3.13(ii) and [Reference KollárKol23, 9.17].
${\rm Spec}\, S$
. Furthermore, it commutes with arbitrary base change by Theorem 3.13(ii) and [Reference KollárKol23, 9.17].
4. Du Bois singularities and liftable local cohomology
In this section we prove a criterion for a local scheme to have liftable
![]() $i^{{th}}\!$
local cohomology for
$i^{{th}}\!$
local cohomology for
![]() $i\geq n-t$
. As before,
$i\geq n-t$
. As before,
![]() $\mathbb{H}^i_x$
denotes
$\mathbb{H}^i_x$
denotes
![]() ${\mathcal{R}}^{\,i}\Gamma _x$
, the
${\mathcal{R}}^{\,i}\Gamma _x$
, the
![]() $i^{{th}}$
derived functor of
$i^{{th}}$
derived functor of
![]() $\Gamma _x$
, the functor of sections with support at
$\Gamma _x$
, the functor of sections with support at
![]() $x$
, i.e., the
$x$
, i.e., the
![]() $i^{{th}}$
local cohomology functor with support at
$i^{{th}}$
local cohomology functor with support at
![]() $x$
on the derived category of quasi-coherent sheaves on
$x$
on the derived category of quasi-coherent sheaves on
![]() $X$
.
$X$
.
Lemma 4.1.
Let
![]() $(X,x)$
be a local scheme of dimension
$(X,x)$
be a local scheme of dimension
![]() $n$
which is essentially of finite type over a field of characteristic
$n$
which is essentially of finite type over a field of characteristic
![]() $0$
. Then
$0$
. Then
![]() $H^i_x({\mathscr{O}}_X)\to \mathbb{H}^i_x({\underline{\Omega }}_X^0)$
is surjective for each
$H^i_x({\mathscr{O}}_X)\to \mathbb{H}^i_x({\underline{\Omega }}_X^0)$
is surjective for each
![]() $i\in \mathbb{Z}$
.
$i\in \mathbb{Z}$
.
Proof. This follows by applying Matlis duality to the map in [Reference Ma, Schwede and ShimomotoMSS17, Lemma 3.2] (cf. [Reference KovácsKov99, Lemma 2.2], [Reference Kovács and SchwedeKS16a, Theorem 3.3], [Reference Kovács and SchwedeKS16b, Theorem 3.2], [Reference Ma, Schwede and ShimomotoMSS17, Lemma 3.3]).
Theorem 4.2.
Let
![]() $(X,x)$
be a local scheme of dimension
$(X,x)$
be a local scheme of dimension
![]() $n$
, which is essentially of finite type over a field of characteristic
$n$
, which is essentially of finite type over a field of characteristic
![]() $0$
. Fix
$0$
. Fix
![]() $t\in \mathbb{N}, t\gt 0$
, and let
$t\in \mathbb{N}, t\gt 0$
, and let
![]() $Z\subseteq X$
be a closed subset of codimension
$Z\subseteq X$
be a closed subset of codimension
![]() $t+2$
. Further let
$t+2$
. Further let
![]() $\sigma : Y\to X$
be an affine morphism which is an isomorphism over
$\sigma : Y\to X$
be an affine morphism which is an isomorphism over
![]() $U\colon \!\!\!= X\setminus Z$
. Assume that
$U\colon \!\!\!= X\setminus Z$
. Assume that
![]() $Y$
is Du Bois. Then
$Y$
is Du Bois. Then
-
(4.2.1)
 $H^i_x({\mathscr{O}}_X)\to \mathbb{H}^i_x({\underline{\Omega }}_X^0)$
is an isomorphism for
$H^i_x({\mathscr{O}}_X)\to \mathbb{H}^i_x({\underline{\Omega }}_X^0)$
is an isomorphism for
 $i\geq n-t$
, and
$i\geq n-t$
, and
-
(4.2.2)
 $X$
has liftable
$X$
has liftable
 $i^{{th}}\!$
local cohomology for
$i^{{th}}\!$
local cohomology for
 $i\geq n-t$
.
$i\geq n-t$
.
Proof.
Let
![]() $W=\sigma ^{-1}(x)\subseteq Y$
, and observe that there is an equality of functors:
$W=\sigma ^{-1}(x)\subseteq Y$
, and observe that there is an equality of functors:
Because
![]() $\sigma$
is an affine morphism, with
$\sigma$
is an affine morphism, with
![]() $\sigma _*$
exact, we obtain an equality of derived functors:
$\sigma _*$
exact, we obtain an equality of derived functors:
Consider the short exact sequence
where
![]() $\mathscr{Q}$
is defined as the cokernel of the first non-zero morphism in this short exact sequence. Applying the functor
$\mathscr{Q}$
is defined as the cokernel of the first non-zero morphism in this short exact sequence. Applying the functor
![]() ${\mathcal{R}}\Gamma _x$
and taking into account (4.2.1), we obtain the following distinguished triangle:
${\mathcal{R}}\Gamma _x$
and taking into account (4.2.1), we obtain the following distinguished triangle:
The assumption implies that
![]() $\mathscr{Q}$
is supported on
$\mathscr{Q}$
is supported on
![]() $Z$
, so
$Z$
, so
![]() $H^i_x(\mathscr{Q})=0$
for
$H^i_x(\mathscr{Q})=0$
for
![]() $i\gt n-t-2$
and hence
$i\gt n-t-2$
and hence
Next, consider the following diagram:

Applying
![]() ${\mathcal{R}}\Gamma _x$
to each element and using (4.2.1) and (4.2.4) leads to the following:
${\mathcal{R}}\Gamma _x$
to each element and using (4.2.1) and (4.2.4) leads to the following:

The top horizontal arrow is an isomorphism for
![]() $i\geq n-t$
, and the right vertical arrow is an isomorphism for all
$i\geq n-t$
, and the right vertical arrow is an isomorphism for all
![]() $i$
because
$i$
because
![]() $Y$
is Du Bois. It follows that the diagonal map is also an isomorphism and, in particular, injective for
$Y$
is Du Bois. It follows that the diagonal map is also an isomorphism and, in particular, injective for
![]() $i\geq n-t$
. In particular the left vertical arrow is also injective for
$i\geq n-t$
. In particular the left vertical arrow is also injective for
![]() $i\geq n-t$
. It is surjective for each
$i\geq n-t$
. It is surjective for each
![]() $i$
by Lemma 4.1 and hence an isomorphism for
$i$
by Lemma 4.1 and hence an isomorphism for
![]() $i\geq n-t$
. This proves (4.2.1).
$i\geq n-t$
. This proves (4.2.1).
Let
![]() $(R,\mathfrak{m})$
be a noetherian local ring and
$(R,\mathfrak{m})$
be a noetherian local ring and
![]() $I\subset R$
a nilpotent ideal such that
$I\subset R$
a nilpotent ideal such that
![]() $R/I\simeq{\mathscr{O}}_{X,x}$
. In order to prove (4.2.2) we need that the induced natural morphism on local cohomology
$R/I\simeq{\mathscr{O}}_{X,x}$
. In order to prove (4.2.2) we need that the induced natural morphism on local cohomology
is surjective for
![]() $i\geq n-t$
. Let
$i\geq n-t$
. Let
![]() $X^{\prime}\colon \!\!\!= {\rm Spec} R$
and consider the following diagram:
$X^{\prime}\colon \!\!\!= {\rm Spec} R$
and consider the following diagram:

As above, the left vertical arrow is a surjection by Lemma 4.1. The bottom horizontal arrow is an isomorphism because
![]() $X^{\prime}_{{\rm red}}\simeq X_{{\rm red}}$
and
$X^{\prime}_{{\rm red}}\simeq X_{{\rm red}}$
and
![]() ${\underline{\Omega }}^0$
depends only on the reduced structure by definition, cf. [Reference Ma, Schwede and ShimomotoMSS17, p.2150]. Finally, the right vertical arrow is an isomorphism for
${\underline{\Omega }}^0$
depends only on the reduced structure by definition, cf. [Reference Ma, Schwede and ShimomotoMSS17, p.2150]. Finally, the right vertical arrow is an isomorphism for
![]() $i\geq n-t$
by (4.2.1), and the combination of these implies (4.2.6) and hence (4.2.2).
$i\geq n-t$
by (4.2.1), and the combination of these implies (4.2.6) and hence (4.2.2).
Proof of Theorem
1.6 It follows from Theorem 4.2 that the assumptions of Theorem 1.6 imply those of Theorem 3.16, which in turn implies the desired statement of Theorem 1.6 if
![]() $S$
is Artinian.
$S$
is Artinian.
If
![]() $\omega _{X/B}$
is known to commute with base changes, then one can check flatness over Artin subschemes of
$\omega _{X/B}$
is known to commute with base changes, then one can check flatness over Artin subschemes of
![]() $B$
by the local criterion of flatness.
$B$
by the local criterion of flatness.
The general case follows from [Reference KollárKol23, 9.17], which is a variant of the local criterion of flatness, combined with obstruction theory.
Proof of Theorem
1.2. We may assume that
![]() $B$
is a local scheme with closed point
$B$
is a local scheme with closed point
![]() $b\in B$
. We will consider three, increasingly more general, cases.
$b\in B$
. We will consider three, increasingly more general, cases.
Case I:
![]() $\Delta=0$
and
$\Delta=0$
and
![]() $\omega _{\widetilde X_b}$
is locally free, where
$\omega _{\widetilde X_b}$
is locally free, where
![]() $\pi :\widetilde X_b\to X_b$
is the demi-normalization as in (1.3.5).
$\pi :\widetilde X_b\to X_b$
is the demi-normalization as in (1.3.5).
Note that
![]() $\omega _{X/B}$
is flat and commutes with arbitrary base change by Theorem 1.6. By further localization we may assume that
$\omega _{X/B}$
is flat and commutes with arbitrary base change by Theorem 1.6. By further localization we may assume that
![]() $\omega _{\widetilde X_b}$
is free. Because
$\omega _{\widetilde X_b}$
is free. Because
![]() $\omega _{X_b}\simeq \pi _*\omega _{\widetilde X_b}$
by Lemma 1.5, we see that
$\omega _{X_b}\simeq \pi _*\omega _{\widetilde X_b}$
by Lemma 1.5, we see that
![]() $\omega _{X/B}$
has a section
$\omega _{X/B}$
has a section
![]() $\sigma$
such that
$\sigma$
such that
![]() $\sigma _b$
does not vanish on
$\sigma _b$
does not vanish on
![]() $U_b$
; hence
$U_b$
; hence
![]() $\sigma :{\mathscr{O}}_{X}\to \omega _{X/B}$
is an isomorphism away from a closed subset
$\sigma :{\mathscr{O}}_{X}\to \omega _{X/B}$
is an isomorphism away from a closed subset
![]() $W$
for which
$W$
for which
![]() $W_b\subset Z_b$
. In particular,
$W_b\subset Z_b$
. In particular,
![]() ${\rm depth}_{W_b}{\mathscr{O}}_X\geq 2$
by (1.2.5). Now we use the easy [Reference KollárKol23, Lem.10.6] to conclude that
${\rm depth}_{W_b}{\mathscr{O}}_X\geq 2$
by (1.2.5). Now we use the easy [Reference KollárKol23, Lem.10.6] to conclude that
![]() ${\mathscr{O}}_{X}\simeq \omega _{X/B}$
. Thus
${\mathscr{O}}_{X}\simeq \omega _{X/B}$
. Thus
![]() $g$
is flat,
$g$
is flat,
![]() $\omega _{X/B}$
is locally free and so are all of its powers.
$\omega _{X/B}$
is locally free and so are all of its powers.
Case II:
![]() $\Delta =D$
is a
$\Delta =D$
is a
![]() $\mathbb{Z}$
-divisor and
$\mathbb{Z}$
-divisor and
![]() $\omega _{\widetilde X_b}(\widetilde D_b)$
is locally free. Note that
$\omega _{\widetilde X_b}(\widetilde D_b)$
is locally free. Note that
![]() ${\mathscr{O}}_U(-D)\simeq \omega _{U/B}$
is flat over
${\mathscr{O}}_U(-D)\simeq \omega _{U/B}$
is flat over
![]() $B$
and commutes with base changes by assumption. Thus Proposition 5.1 applies, so
$B$
and commutes with base changes by assumption. Thus Proposition 5.1 applies, so
![]() $\omega _{X/B}(D)$
is flat over
$\omega _{X/B}(D)$
is flat over
![]() $B$
and commutes with base changes.
$B$
and commutes with base changes.
We may assume that
![]() $\omega _{\widetilde X_b}(\widetilde D_b)$
is free with generating section
$\omega _{\widetilde X_b}(\widetilde D_b)$
is free with generating section
![]() $\widetilde \sigma _b$
. By Lemma 1.5 we can identify
$\widetilde \sigma _b$
. By Lemma 1.5 we can identify
![]() $\widetilde \sigma _b$
with a section
$\widetilde \sigma _b$
with a section
![]() $\sigma _b$
of
$\sigma _b$
of
![]() $\omega _{X_b}(D_b)$
. By flatness it lifts to
$\omega _{X_b}(D_b)$
. By flatness it lifts to
![]() $\sigma :{\mathscr{O}}_X\to \omega _{X/B}(D)$
, which is an isomorphism over
$\sigma :{\mathscr{O}}_X\to \omega _{X/B}(D)$
, which is an isomorphism over
![]() $U$
. By (1.2.5) (and the easy [Reference KollárKol23, 10.6]),
$U$
. By (1.2.5) (and the easy [Reference KollárKol23, 10.6]),
![]() $\sigma$
is an isomorphism. Thus
$\sigma$
is an isomorphism. Thus
![]() $\omega _{X/B}(D)$
is locally free and so are its powers.
$\omega _{X/B}(D)$
is locally free and so are its powers.
Case III: The general case. We may assume that
![]() $X$
is local, and by [Reference KollárKol23, 9.17] it is sufficient to prove the case when
$X$
is local, and by [Reference KollárKol23, 9.17] it is sufficient to prove the case when
![]() $B$
is Artinian.
$B$
is Artinian.
Write
![]() $\Delta =\sum _{i\in I} a_iD_i$
, where
$\Delta =\sum _{i\in I} a_iD_i$
, where
![]() $a_i=1-\frac 1{i}$
,
$a_i=1-\frac 1{i}$
,
![]() $I\subset \{2, 3,4, \dots, \infty \}$
is a finite subset and the
$I\subset \{2, 3,4, \dots, \infty \}$
is a finite subset and the
![]() $D_i$
are reduced divisors.
$D_i$
are reduced divisors.
Choose
![]() $m\gt 0$
such that
$m\gt 0$
such that
![]() $\omega _{U_b}^{[m]}(m\Delta _b)\sim{\mathscr{O}}_{U_b}$
. The kernel of
$\omega _{U_b}^{[m]}(m\Delta _b)\sim{\mathscr{O}}_{U_b}$
. The kernel of
![]() ${\rm Pic}(U)\to {\rm Pic}(U_b)$
is a
${\rm Pic}(U)\to {\rm Pic}(U_b)$
is a
![]() $k$
-vectorspace and is hence divisible and torsion free. Thus there is a unique line bundle
$k$
-vectorspace and is hence divisible and torsion free. Thus there is a unique line bundle
![]() $L_U$
on
$L_U$
on
![]() $U$
such that
$U$
such that
![]() $L_{U_b}\sim{\mathscr{O}}_{U_b}$
and
$L_{U_b}\sim{\mathscr{O}}_{U_b}$
and
![]() $\omega _{U/B}^{[m]}(m\Delta )[\otimes ] L^{m}_U\sim{\mathscr{O}}_U$
. Let
$\omega _{U/B}^{[m]}(m\Delta )[\otimes ] L^{m}_U\sim{\mathscr{O}}_U$
. Let
![]() $L$
be the push-forward of
$L$
be the push-forward of
![]() $L_U$
to
$L_U$
to
![]() $X$
. Take the corresponding cyclic cover
$X$
. Take the corresponding cyclic cover
Note that
![]() $\pi$
ramifies along the
$\pi$
ramifies along the
![]() $D_i$
as follows. If
$D_i$
as follows. If
![]() $i\geq 3$
, then
$i\geq 3$
, then
![]() $\pi$
has ramification index
$\pi$
has ramification index
![]() $i$
along
$i$
along
![]() $D_i$
, and
$D_i$
, and
![]() $\pi$
is unramified along
$\pi$
is unramified along
![]() $D_{\infty }$
. The
$D_{\infty }$
. The
![]() $i=2$
case is somewehat special. Then
$i=2$
case is somewehat special. Then
![]() $\pi _b$
has ramification index
$\pi _b$
has ramification index
![]() $2$
along an irreducible divisor
$2$
along an irreducible divisor
![]() $F_b\subset X_b$
if it has multiplicity 1 in
$F_b\subset X_b$
if it has multiplicity 1 in
![]() $D_2|_b$
, and
$D_2|_b$
, and
![]() $Y_b$
is nodal along
$Y_b$
is nodal along
![]() $\pi _b^{-1}(F_b)$
if
$\pi _b^{-1}(F_b)$
if
![]() $F_b$
has multiplicity 2 in
$F_b$
has multiplicity 2 in
![]() $D_2|_b$
. Thus
$D_2|_b$
. Thus
In particular,
![]() $(Y, \pi ^*D_{\infty } )\to B$
satisfies the assumptions (1.2.1)–(1.2.6). (Note that
$(Y, \pi ^*D_{\infty } )\to B$
satisfies the assumptions (1.2.1)–(1.2.6). (Note that
![]() $Y\to B$
is known to be flat only over
$Y\to B$
is known to be flat only over
![]() $U$
, so requiring flatness only in codimension
$U$
, so requiring flatness only in codimension
![]() $\leq 2$
is essential here.)
$\leq 2$
is essential here.)
By duality, we get that
 \begin{align*} \begin {array}{lcl} \pi _* \omega _{Y/B}(\pi ^*D_{\infty } )&\simeq & \textstyle {\sum }_{j=0}^{m-1} \omega _{X/B}^{[1-j]} \bigl (D_{\infty }-\textstyle {\sum }_i \lfloor {ja_i}\rfloor D_i\bigr )[\otimes ] L^{[-j]}, \quad \mbox {and}\quad \\[5pt] (\pi _b)_* \omega _{\widetilde Y_b}(\pi _b^*D_{\infty } )&\simeq & \textstyle {\sum }_{j=0}^{m-1} \omega _{X_b}^{[1-j]} \bigl (D_{\infty }|_b-\textstyle {\sum }_i \lfloor {ja_i}\rfloor D_i|_b\bigr )[\otimes ] L^{[-j]}_b. \end {array} \end{align*}
\begin{align*} \begin {array}{lcl} \pi _* \omega _{Y/B}(\pi ^*D_{\infty } )&\simeq & \textstyle {\sum }_{j=0}^{m-1} \omega _{X/B}^{[1-j]} \bigl (D_{\infty }-\textstyle {\sum }_i \lfloor {ja_i}\rfloor D_i\bigr )[\otimes ] L^{[-j]}, \quad \mbox {and}\quad \\[5pt] (\pi _b)_* \omega _{\widetilde Y_b}(\pi _b^*D_{\infty } )&\simeq & \textstyle {\sum }_{j=0}^{m-1} \omega _{X_b}^{[1-j]} \bigl (D_{\infty }|_b-\textstyle {\sum }_i \lfloor {ja_i}\rfloor D_i|_b\bigr )[\otimes ] L^{[-j]}_b. \end {array} \end{align*}
The
![]() $j=1$
summand of
$j=1$
summand of
![]() $(\pi _b)_* \omega _{\widetilde Y_b}(\pi _b^*D_{\infty } )$
is trivial. Thus
$(\pi _b)_* \omega _{\widetilde Y_b}(\pi _b^*D_{\infty } )$
is trivial. Thus
![]() $\omega _{\widetilde Y_b}(\pi _b^*D_{\infty } )$
has a section that is nowhere zero on
$\omega _{\widetilde Y_b}(\pi _b^*D_{\infty } )$
has a section that is nowhere zero on
![]() $U_b$
, so
$U_b$
, so
![]() $\omega _{\widetilde Y_b}(\pi _b^*D_{\infty } )$
is trivial. The previous case applies, and we conclude that all the
$\omega _{\widetilde Y_b}(\pi _b^*D_{\infty } )$
is trivial. The previous case applies, and we conclude that all the
are flat over
![]() $B$
and commute with base changes.
$B$
and commute with base changes.
The
![]() $j=1$
summand is
$j=1$
summand is
![]() $L^{[-1]}$
, whose restriction to
$L^{[-1]}$
, whose restriction to
![]() $X_b$
is trivial. By flatness, the constant 1 section of
$X_b$
is trivial. By flatness, the constant 1 section of
![]() $L^{[-1]}\vert _{X_b}$
lifts to a section of
$L^{[-1]}\vert _{X_b}$
lifts to a section of
![]() $L^{[-1]}$
; hence
$L^{[-1]}$
; hence
![]() $L$
is trivial.
$L$
is trivial.
Now fix
![]() $0\leq r\lt m$
and set
$0\leq r\lt m$
and set
![]() $1-j=r-m$
. Then we get that
$1-j=r-m$
. Then we get that
is flat over
![]() $B$
and commutes with base changes. Now, observe that
$B$
and commutes with base changes. Now, observe that
 \begin{align*} \lfloor {ra}\rfloor +\lfloor {(m-r+1)a}\rfloor = \begin {cases} m+1 \quad \mbox {if}\quad a=1, \quad \mbox {and}\quad \\ m \quad \mbox {if}\quad a=\tfrac {c-1}{c} \quad \mbox {for some}\quad 1\lt c\mid m. \end {cases} \end{align*}
\begin{align*} \lfloor {ra}\rfloor +\lfloor {(m-r+1)a}\rfloor = \begin {cases} m+1 \quad \mbox {if}\quad a=1, \quad \mbox {and}\quad \\ m \quad \mbox {if}\quad a=\tfrac {c-1}{c} \quad \mbox {for some}\quad 1\lt c\mid m. \end {cases} \end{align*}
This gives that
Thus the
![]() $\omega _{X/B}^{[r]} \bigl (\textstyle{\sum }_i \lfloor{ra_i}\rfloor D_i\bigr )$
are flat over
$\omega _{X/B}^{[r]} \bigl (\textstyle{\sum }_i \lfloor{ra_i}\rfloor D_i\bigr )$
are flat over
![]() $B$
and commute with base changes.
$B$
and commute with base changes.
Corollary 4.3.
Using the notation and assumptions of Theorem 1.2
, set
![]() $D_\infty :=\sum _{i:a_i=1}D_i$
. Then
$D_\infty :=\sum _{i:a_i=1}D_i$
. Then
![]() ${\mathscr{O}}_X(-D_\infty )$
and
${\mathscr{O}}_X(-D_\infty )$
and
![]() ${\mathscr{O}}_{D_\infty }$
are flat over
${\mathscr{O}}_{D_\infty }$
are flat over
![]() $B$
and commute with base changes.
$B$
and commute with base changes.
Proof. Arguing as in Case III above, we get that
We proved that
![]() $L$
is trivial, so the
$L$
is trivial, so the
![]() $j=1$
summand is
$j=1$
summand is
![]() ${\mathscr{O}}_X(-D_\infty )$
. It is thus flat over
${\mathscr{O}}_X(-D_\infty )$
. It is thus flat over
![]() $B$
with
$B$
with
![]() $S_2$
fibers. Therefore, the induced maps
$S_2$
fibers. Therefore, the induced maps
![]() ${\mathscr{O}}_X(-D_\infty )|_{X_b}\to{\mathscr{O}}_{X_b}$
are injections; hence
${\mathscr{O}}_X(-D_\infty )|_{X_b}\to{\mathscr{O}}_{X_b}$
are injections; hence
![]() ${\mathscr{O}}_{D_\infty }$
is also flat over
${\mathscr{O}}_{D_\infty }$
is also flat over
![]() $B$
and commutes with base changes.
$B$
and commutes with base changes.
5. KSBA stability
It is possible that the analog of Theorem 1.2 holds for arbitrary KSBA stable pairs as in [Reference KollárKol23, Sec. 8.2]. Note that by [Reference KollárKol23, 7.5], K-flatness of divisors is automatic in codimension
![]() $\geq 3$
. This would mean that the whole theory of KSBA stability is determined in codimension 2.
$\geq 3$
. This would mean that the whole theory of KSBA stability is determined in codimension 2.
The next result is a very small step in this direction. It shows that the reduced part of the boundary divisor behaves well in codimension
![]() $\geq 3$
.
$\geq 3$
.
Proposition 5.1.
Let
![]() $g:X\to B$
be a morphism of finite type and of pure relative dimension over a field of characteristic 0,
$g:X\to B$
be a morphism of finite type and of pure relative dimension over a field of characteristic 0,
![]() $\Delta$
be a relative Mumford
$\Delta$
be a relative Mumford
![]() $\mathbb{R}$
-divisor and be
$\mathbb{R}$
-divisor and be
![]() $0\leq D\leq \Delta$
a relative Mumford
$0\leq D\leq \Delta$
a relative Mumford
![]() $\mathbb{Z}$
-divisor. Let
$\mathbb{Z}$
-divisor. Let
![]() $Z\subset X$
be a closed subset, and set
$Z\subset X$
be a closed subset, and set
![]() $U:=X\setminus Z$
. Assume that
$U:=X\setminus Z$
. Assume that
-
(5.1.1)
 ${\rm codim} (Z_b\subset X_b)\geq 3$
for every
${\rm codim} (Z_b\subset X_b)\geq 3$
for every
 $b\in B$
,
$b\in B$
, -
(5.1.2)
 $g\vert _{U}: U\to B$
is flat with demi-normal fibers,
$g\vert _{U}: U\to B$
is flat with demi-normal fibers,
-
(5.1.3)
 ${\mathscr{O}}_U(-D|_U)$
is flat over
${\mathscr{O}}_U(-D|_U)$
is flat over
 $B$
and commutes with base changes, and
$B$
and commutes with base changes, and
-
(5.1.4) the demi-normalization
 $(\widetilde X_b, \widetilde \Delta _b)$
of
$(\widetilde X_b, \widetilde \Delta _b)$
of
 $ (X_b, \Delta _b)$
is semi-log-canonical for
$ (X_b, \Delta _b)$
is semi-log-canonical for
 $b\in B$
.
$b\in B$
.
Then
![]() $\omega _{X/B}(D)$
is flat over
$\omega _{X/B}(D)$
is flat over
![]() $B$
and commutes with base changes.
$B$
and commutes with base changes.
Proof.
Take two copies
![]() $(X_i,\Delta _i)\simeq (X, \Delta )$
, and glue them together along
$(X_i,\Delta _i)\simeq (X, \Delta )$
, and glue them together along
![]() $D_1\simeq D_2$
to get
$D_1\simeq D_2$
to get
Let
![]() $\pi :Y\to X$
be the projection. Set
$\pi :Y\to X$
be the projection. Set
![]() $\Delta _Y:=\pi ^*(\Delta -D)$
, and consider the short exact sequence
$\Delta _Y:=\pi ^*(\Delta -D)$
, and consider the short exact sequence
Because
![]() $\pi$
is finite, the push-forward of this remains exact, and using the fact that
$\pi$
is finite, the push-forward of this remains exact, and using the fact that
![]() $\pi \vert _{X_i}$
is an isomorphism, the natural morphism
$\pi \vert _{X_i}$
is an isomorphism, the natural morphism
![]() ${\mathscr{O}}_X\to \pi _*{\mathscr{O}}_Y$
provides a splitting of the push-forward of the above exact sequence. Therefore,
${\mathscr{O}}_X\to \pi _*{\mathscr{O}}_Y$
provides a splitting of the push-forward of the above exact sequence. Therefore,
![]() $\pi _*{\mathscr{O}}_Y\simeq{\mathscr{O}}_X\oplus{\mathscr{O}}_X(-D)$
, so
$\pi _*{\mathscr{O}}_Y\simeq{\mathscr{O}}_X\oplus{\mathscr{O}}_X(-D)$
, so
![]() $(Y,\Delta _Y) \to B$
is flat over
$(Y,\Delta _Y) \to B$
is flat over
![]() $\pi ^{-1}(U)$
with semi-log-canonical fibers. The demi-normalization of
$\pi ^{-1}(U)$
with semi-log-canonical fibers. The demi-normalization of
![]() $(Y_b, \Delta _Y|_b)$
is the amalgamation of two copies of
$(Y_b, \Delta _Y|_b)$
is the amalgamation of two copies of
![]() $\bigl (\widetilde X_b, \widetilde \Delta _b\bigr )$
along
$\bigl (\widetilde X_b, \widetilde \Delta _b\bigr )$
along
![]() $\widetilde D_b$
, hence semi-log-canonical. Thus
$\widetilde D_b$
, hence semi-log-canonical. Thus
![]() $\omega _{Y/B}$
is flat over
$\omega _{Y/B}$
is flat over
![]() $B$
and commutes with base changes by Theorem 1.6. Finally note that
$B$
and commutes with base changes by Theorem 1.6. Finally note that
![]() $\pi _*\omega _{Y/B}\simeq \omega _{X/B}\oplus \omega _{X/B}(D)$
; thus
$\pi _*\omega _{Y/B}\simeq \omega _{X/B}\oplus \omega _{X/B}(D)$
; thus
![]() $\omega _{X/B}(D)$
is flat over
$\omega _{X/B}(D)$
is flat over
![]() $B$
and commutes with base changes.
$B$
and commutes with base changes.
Remark 5.2. We claim that AFI stability, where we float all coefficients as in [Reference KollárKol23, Sec. 8.3], is determined in codimension 2.
To see this, note that the boundary divisor
![]() $\Delta$
is necessarily
$\Delta$
is necessarily
![]() $\mathbb{R}$
-Cartier. Thus, for every point
$\mathbb{R}$
-Cartier. Thus, for every point
![]() $x\in Z_b$
as in Theorem 1.2, either
$x\in Z_b$
as in Theorem 1.2, either
![]() $x\not \in {\rm supp} \Delta _b$
, and then local stability holds by Theorem 1.2, or
$x\not \in {\rm supp} \Delta _b$
, and then local stability holds by Theorem 1.2, or
![]() $x\in {\rm supp} \Delta _b$
, and then
$x\in {\rm supp} \Delta _b$
, and then
![]() $x$
is not an lc center of
$x$
is not an lc center of
![]() $X_b$
. Then
$X_b$
. Then
![]() ${\rm depth}_x{\mathscr{O}}_{\widetilde X_b}\geq 3$
by [Reference KollárKol13b, 7.20] (cf. [Reference KovácsKov11] and [Reference Alexeev and HaconAH12]); hence local stability holds by [Reference KollárKol23, 10.73].
${\rm depth}_x{\mathscr{O}}_{\widetilde X_b}\geq 3$
by [Reference KollárKol13b, 7.20] (cf. [Reference KovácsKov11] and [Reference Alexeev and HaconAH12]); hence local stability holds by [Reference KollárKol23, 10.73].
Conflicts of Interest
None.
Funding Statement
János Kollár was supported in part by NSF Grant DMS-1901855. Sándor Kovács was supported in part by NSF Grants DMS-1951376,-2100389 and a Simons Fellowship.
Journal Information
Moduli is published as a joint venture of the Foundation Compositio Mathematica and the London Mathematical Society. As not-for-profit organisations, the Foundation and Society reinvest 100% of any surplus generated from their publications back into mathematics through their charitable activities.