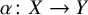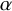1 Introduction
Motivated by the study of the theta linear series on the moduli spaces of vector bundles on curves, Beauville in [Reference BeauvilleB00] (see also [Reference BeauvilleB06, Conjecture 6.5]) made the following celebrated conjecture:
Conjecture 1.1 (Beauville).
Let
![]() $\alpha \colon X \to Y$
be a finite morphism between smooth irreducible projective curves, and let V be a general vector bundle on X. Then
$\alpha \colon X \to Y$
be a finite morphism between smooth irreducible projective curves, and let V be a general vector bundle on X. Then
![]() $\alpha _* V$
is stable if the genus of Y is at least
$\alpha _* V$
is stable if the genus of Y is at least
![]() $2$
and semistable if the genus of Y is
$2$
and semistable if the genus of Y is
![]() $1$
.
$1$
.
We prove Beauville’s conjecture when Y is an arbitrary smooth irreducible projective curve and X is a general member of any component of the Hurwitz space of genus g degree r covers of Y.
Statement of results
Let
![]() $\alpha \colon X \to Y$
be a finite map of degree r from a smooth irreducible projective curve X of genus g to a smooth irreducible projective curve Y of genus h. We always work over an algebraically closed field of characteristic 0 or greater than r.
$\alpha \colon X \to Y$
be a finite map of degree r from a smooth irreducible projective curve X of genus g to a smooth irreducible projective curve Y of genus h. We always work over an algebraically closed field of characteristic 0 or greater than r.
For a vector bundle V on a curve X, the slope
![]() $\mu (V)$
is defined by
$\mu (V)$
is defined by
![]() $\mu (V) = \frac {\deg (V)}{\operatorname {rk}(V)}$
. The bundle V is called (semi)stable if, for every proper subbundle W, we have
$\mu (V) = \frac {\deg (V)}{\operatorname {rk}(V)}$
. The bundle V is called (semi)stable if, for every proper subbundle W, we have
![]() $\mu (W) \underset {{\scriptscriptstyle (}-{\scriptscriptstyle )}}{<} \mu (V)$
. Semistable bundles satisfy nice cohomological and metric properties and form projective moduli spaces. Consequently, determining the stability of naturally defined bundles is an important and fundamental problem.
$\mu (W) \underset {{\scriptscriptstyle (}-{\scriptscriptstyle )}}{<} \mu (V)$
. Semistable bundles satisfy nice cohomological and metric properties and form projective moduli spaces. Consequently, determining the stability of naturally defined bundles is an important and fundamental problem.
Let
![]() $\mathscr {H}_{r,g}(Y)$
denote the Hurwitz space parameterizing smooth connected degree r genus g covers of Y. In general,
$\mathscr {H}_{r,g}(Y)$
denote the Hurwitz space parameterizing smooth connected degree r genus g covers of Y. In general,
![]() $\mathscr {H}_{r,g}(Y)$
is reducible, and when
$\mathscr {H}_{r,g}(Y)$
is reducible, and when
![]() $g> r(h-1) + 1$
, the irreducible components correspond to subgroups of the (étale) fundamental group
$g> r(h-1) + 1$
, the irreducible components correspond to subgroups of the (étale) fundamental group
![]() $\pi _1(Y)$
of index diving r. With this notation, our main theorem is the following.
$\pi _1(Y)$
of index diving r. With this notation, our main theorem is the following.
Theorem 1.2. Let Y be any smooth irreducible projective curve of genus h. Let
![]() $\alpha \colon X \to Y$
be a general morphism in any component of
$\alpha \colon X \to Y$
be a general morphism in any component of
![]() $\mathscr {H}_{r,g}(Y)$
. Let V be a general vector bundle of any degree and rank on X.
$\mathscr {H}_{r,g}(Y)$
. Let V be a general vector bundle of any degree and rank on X.
-
1. If
 $h=1$
, then
$h=1$
, then
 $\alpha _*V$
is semistable.
$\alpha _*V$
is semistable. -
2. If
 $h\geq 2$
, then
$h\geq 2$
, then
 $\alpha _*V$
is stable.
$\alpha _*V$
is stable.
Remark 1.3. It may happen that, for special V, the bundle
![]() $\alpha _* V$
is not semistable. For example,
$\alpha _* V$
is not semistable. For example,
![]() $\alpha _* \mathcal {O}_X$
has
$\alpha _* \mathcal {O}_X$
has
![]() $\mathcal {O}_Y$
as a direct summand. When the map
$\mathcal {O}_Y$
as a direct summand. When the map
![]() $\alpha $
is ramified,
$\alpha $
is ramified,
![]() $\mathcal {O}_Y$
destabilizes
$\mathcal {O}_Y$
destabilizes
![]() $\alpha _* \mathcal {O}_X$
(see [Reference Coskun, Larson and VogtCLV22]).
$\alpha _* \mathcal {O}_X$
(see [Reference Coskun, Larson and VogtCLV22]).
History of the problem
Beauville made Conjecture 1.1 in an unpublished note dating to 2000 [Reference BeauvilleB00]. In the same note, Beauville proved the conjecture if
-
1.
 $\alpha $
is étale [Reference BeauvilleB00, Propostion 4.1], or
$\alpha $
is étale [Reference BeauvilleB00, Propostion 4.1], or -
2.
 $r < g (\sqrt {3} + 1) -1$
[Reference BeauvilleB00, Corollary 3.4], or
$r < g (\sqrt {3} + 1) -1$
[Reference BeauvilleB00, Corollary 3.4], or -
3. V is a line bundle with
 $|\chi (V)| \leq g + \frac {g^2}{r}$
[Reference BeauvilleB00, Proposition 3.2].
$|\chi (V)| \leq g + \frac {g^2}{r}$
[Reference BeauvilleB00, Proposition 3.2].
It is an elementary observation that, when
![]() $h=0$
, the pushforward of a general vector bundle splits as
$h=0$
, the pushforward of a general vector bundle splits as
![]() $\bigoplus _{i=1}^r \mathcal {O}_{\mathbb {P}^1}(a_i)$
, where
$\bigoplus _{i=1}^r \mathcal {O}_{\mathbb {P}^1}(a_i)$
, where
![]() $|a_i-a_j| \leq 1$
for every
$|a_i-a_j| \leq 1$
for every
![]() $i,j$
(see [Reference BeauvilleB00, §1]).
$i,j$
(see [Reference BeauvilleB00, §1]).
Beauville, Narasimhan and Ramanan [Reference Beauville, Narasimhan and RamananBNR89] earlier proved that a general vector bundle V of degree d and rank r on Y arises as the pushforward of a line bundle from some cover of degree r. Hence, there exists covers of Y for which Beauville’s conjecture is true.
Mehta and Pauly [Reference Mehta and PaulyMP07] proved that if
![]() $\alpha $
is the Frobenius morphism,
$\alpha $
is the Frobenius morphism,
![]() $h\geq 2$
, and V is semistable, then
$h\geq 2$
, and V is semistable, then
![]() $\alpha _* V$
is semistable.
$\alpha _* V$
is semistable.
Strategy
Recall that
![]() $\alpha \colon X \to Y$
is called primitive if the map
$\alpha \colon X \to Y$
is called primitive if the map
![]() $\alpha _*\colon \pi _1(X) \to \pi _1(Y)$
induced on (étale) fundamental groups is surjective. Every degree r cover
$\alpha _*\colon \pi _1(X) \to \pi _1(Y)$
induced on (étale) fundamental groups is surjective. Every degree r cover
![]() $\alpha \colon X \to Y$
factors into a primitive map
$\alpha \colon X \to Y$
factors into a primitive map
![]() $\alpha ^{\text {pr}} \colon X \to Y'$
followed by an étale map
$\alpha ^{\text {pr}} \colon X \to Y'$
followed by an étale map
![]() $\alpha ^{\text {\'et}}\colon Y' \to Y$
, where
$\alpha ^{\text {\'et}}\colon Y' \to Y$
, where
![]() $Y'$
is the étale cover associated with the subgroup
$Y'$
is the étale cover associated with the subgroup
![]() $\alpha _*\pi _1(X) \subset \pi _1(Y)$
.
$\alpha _*\pi _1(X) \subset \pi _1(Y)$
.
We prove Theorem 1.2 by specializing X to a nodal curve. Let
![]() $\alpha \colon X \to Y$
be a general element in any component of
$\alpha \colon X \to Y$
be a general element in any component of
![]() $\mathscr {H}_{r,g}(Y)$
. Let
$\mathscr {H}_{r,g}(Y)$
. Let
![]() $\alpha = \alpha ^{\text {pr}} \circ \alpha ^{\text {\'et}}$
be the primitive-étale factorization of
$\alpha = \alpha ^{\text {pr}} \circ \alpha ^{\text {\'et}}$
be the primitive-étale factorization of
![]() $\alpha $
. Let
$\alpha $
. Let
![]() $\alpha ^{\text {\'et}}$
and
$\alpha ^{\text {\'et}}$
and
![]() $\alpha ^{\text {pr}}$
have degrees
$\alpha ^{\text {pr}}$
have degrees
![]() $r'$
and
$r'$
and
![]() $s= \frac {r}{r'}$
, respectively. Let
$s= \frac {r}{r'}$
, respectively. Let
![]() $\beta _0\colon X_0 \to Y'$
be a degree s cyclic étale cover of
$\beta _0\colon X_0 \to Y'$
be a degree s cyclic étale cover of
![]() $Y'$
. The resulting map
$Y'$
. The resulting map
![]() $\alpha _0 \colon X_0 \to Y$
is étale and Conjecture 1.1 holds for the map
$\alpha _0 \colon X_0 \to Y$
is étale and Conjecture 1.1 holds for the map
![]() $X_0 \to Y$
by [Reference BeauvilleB00, Proposition 4.1].
$X_0 \to Y$
by [Reference BeauvilleB00, Proposition 4.1].
Let
![]() $p_{j}$
and
$p_{j}$
and
![]() $p_{j}'$
be points on
$p_{j}'$
be points on
![]() $X_0$
contained in a fiber of
$X_0$
contained in a fiber of
![]() $\beta _0$
such that the cyclic action takes
$\beta _0$
such that the cyclic action takes
![]() $p_{j}$
to
$p_{j}$
to
![]() $p_{j}'$
. We identify the appropriate number of pairs
$p_{j}'$
. We identify the appropriate number of pairs
![]() $p_{j}$
and
$p_{j}$
and
![]() $p_{j}'$
on
$p_{j}'$
on
![]() $X_0$
to form a nodal curve
$X_0$
to form a nodal curve
![]() $X_1$
of genus g. Let
$X_1$
of genus g. Let
![]() $\nu \colon X_0 \to X_1$
be the normalization map. The induced map
$\nu \colon X_0 \to X_1$
be the normalization map. The induced map
![]() $\beta _1\colon X_1 \to Y'$
is primitive (see Proposition 3.1), and so
$\beta _1\colon X_1 \to Y'$
is primitive (see Proposition 3.1), and so
![]() $\alpha _1= \alpha ^{\text {\'et}} \circ \beta _1\colon X_1 \to Y$
is in the same irreducible component of
$\alpha _1= \alpha ^{\text {\'et}} \circ \beta _1\colon X_1 \to Y$
is in the same irreducible component of
![]() $\mathscr {H}_{r,g}(Y)$
as X (see Lemma 2.1). For a general bundle V on
$\mathscr {H}_{r,g}(Y)$
as X (see Lemma 2.1). For a general bundle V on
![]() $X_0$
, the pushforward
$X_0$
, the pushforward
![]() ${\alpha _0}_*V={\alpha _1}_* (\nu _* V)$
is stable if
${\alpha _0}_*V={\alpha _1}_* (\nu _* V)$
is stable if
![]() $h \geq 2$
and semistable if
$h \geq 2$
and semistable if
![]() $h=1$
. Finally, we observe that
$h=1$
. Finally, we observe that
![]() $\nu _* V$
is a limit of vector bundles on nearby deformations of
$\nu _* V$
is a limit of vector bundles on nearby deformations of
![]() $X_1$
(see Proposition 3.2). Together with the openness of (semi)stability, this proves Theorem 1.2.
$X_1$
(see Proposition 3.2). Together with the openness of (semi)stability, this proves Theorem 1.2.
2 Preliminaries
2.1 Basic facts
Let
![]() $\alpha \colon X \to Y$
be a finite map of degree r from a smooth irreducible projective curve X of genus g to a smooth irreducible projective curve Y of genus h. Since the characteristic is 0 or greater than r, the map
$\alpha \colon X \to Y$
be a finite map of degree r from a smooth irreducible projective curve X of genus g to a smooth irreducible projective curve Y of genus h. Since the characteristic is 0 or greater than r, the map
![]() $\alpha $
is separable. By the Riemann–Hurwitz formula
$\alpha $
is separable. By the Riemann–Hurwitz formula
where b is the degree of the ramification divisor. In particular,
![]() $g \geq r(h-1) + 1$
with equality if and only if
$g \geq r(h-1) + 1$
with equality if and only if
![]() $\alpha $
is étale.
$\alpha $
is étale.
If V is a vector bundle of rank s and degree d on X, then
![]() $\alpha _*(V)$
is a vector bundle of rank
$\alpha _*(V)$
is a vector bundle of rank
![]() $rs$
on Y. Using the fact that
$rs$
on Y. Using the fact that
![]() $\chi (V)= \chi (\alpha _*V)$
and the Riemann–Roch formula, we compute the degree
$\chi (V)= \chi (\alpha _*V)$
and the Riemann–Roch formula, we compute the degree
![]() $d'$
of
$d'$
of
![]() $\alpha _*(V)$
via
$\alpha _*(V)$
via
We conclude that
![]() $d' = d+ s(1-g) - rs(1-h).$
$d' = d+ s(1-g) - rs(1-h).$
2.2 The primitive-étale factorization
Let
![]() $\mathscr {H}_{r,g}(Y)$
denote the Hurwitz space parameterizing smooth connected degree r genus g covers of Y. If
$\mathscr {H}_{r,g}(Y)$
denote the Hurwitz space parameterizing smooth connected degree r genus g covers of Y. If
![]() $g < r(h-1)+1$
, then
$g < r(h-1)+1$
, then
![]() $\mathscr {H}_{r,g}(Y)$
is empty. If
$\mathscr {H}_{r,g}(Y)$
is empty. If
![]() $g=r(h-1)+1$
, then the degree r covers of genus g are étale and there are finitely many. In general, the Hurwitz space
$g=r(h-1)+1$
, then the degree r covers of genus g are étale and there are finitely many. In general, the Hurwitz space
![]() $\mathscr {H}_{r,g}(Y)$
is not irreducible. The following lemma characterizes the irreducible components.
$\mathscr {H}_{r,g}(Y)$
is not irreducible. The following lemma characterizes the irreducible components.
Lemma 2.1. Let Y be a smooth and irreducible curve of genus h defined over an algebraically closed field of characteristic
![]() $0$
or larger than r. Let
$0$
or larger than r. Let
![]() $g> r(h-1) + 1$
. Then the components of
$g> r(h-1) + 1$
. Then the components of
![]() $\mathscr {H}_{r,g}(Y)$
are in bijection with subgroups of
$\mathscr {H}_{r,g}(Y)$
are in bijection with subgroups of
![]() $\pi _1(Y)$
of index dividing r.
$\pi _1(Y)$
of index dividing r.
Proof. Let
![]() $\mathscr {H}$
be an irreducible component of the Hurwitz scheme
$\mathscr {H}$
be an irreducible component of the Hurwitz scheme
![]() $\mathscr {H}_{r,g}(Y)$
. Given
$\mathscr {H}_{r,g}(Y)$
. Given
![]() $\alpha \colon X \to Y$
in
$\alpha \colon X \to Y$
in
![]() $\mathscr {H}$
, the subgroup
$\mathscr {H}$
, the subgroup
![]() $\alpha _* \pi _1(X)$
of
$\alpha _* \pi _1(X)$
of
![]() $\pi _1(Y)$
has index dividing r. Since this is a discrete invariant and is constant in irreducible families,
$\pi _1(Y)$
has index dividing r. Since this is a discrete invariant and is constant in irreducible families,
![]() $\alpha _* \pi _1(X)$
is an invariant of
$\alpha _* \pi _1(X)$
is an invariant of
![]() $\mathscr {H}$
.
$\mathscr {H}$
.
Conversely, given a subgroup
![]() $G \subset \pi _1(Y)$
of index
$G \subset \pi _1(Y)$
of index
![]() $r^{\text {\'et}}$
dividing r, up to isomorphism there is a unique étale cover
$r^{\text {\'et}}$
dividing r, up to isomorphism there is a unique étale cover
![]() $\delta \colon Y' \to Y$
corresponding to G of degree
$\delta \colon Y' \to Y$
corresponding to G of degree
![]() $r^{\text {\'et}}$
and genus
$r^{\text {\'et}}$
and genus
![]() $h' = r^{\text {\'et}}(h-1) + 1$
. Let
$h' = r^{\text {\'et}}(h-1) + 1$
. Let
![]() $r^{\text {pr}} = r/r^{\text {\'et}}$
. Given the inequality
$r^{\text {pr}} = r/r^{\text {\'et}}$
. Given the inequality
there exists a genus g primitive cover
![]() $\gamma \colon X \to Y'$
of degree
$\gamma \colon X \to Y'$
of degree
![]() $r^{\text {pr}}$
. For any such cover, we obtain an element of
$r^{\text {pr}}$
. For any such cover, we obtain an element of
![]() $\mathscr {H}_{r,g}(Y)$
by taking
$\mathscr {H}_{r,g}(Y)$
by taking
![]() $\alpha = \delta \circ \gamma $
. Furthermore,
$\alpha = \delta \circ \gamma $
. Furthermore,
![]() $\alpha _* \pi _1(X) = G$
. On the other hand, if
$\alpha _* \pi _1(X) = G$
. On the other hand, if
![]() $\gamma \colon X \to Y'$
is not primitive but
$\gamma \colon X \to Y'$
is not primitive but
![]() $\gamma _* \pi _1(X)$
has index s in
$\gamma _* \pi _1(X)$
has index s in
![]() $\pi _1(Y')$
, then
$\pi _1(Y')$
, then
![]() $\alpha _* \pi _1(X)$
has index
$\alpha _* \pi _1(X)$
has index
![]() $s r^{\text {\'et}}$
in
$s r^{\text {\'et}}$
in
![]() $\pi _1(Y)$
and cannot be G. We conclude that if
$\pi _1(Y)$
and cannot be G. We conclude that if
![]() $\alpha _*\pi _1(X)=G$
, then
$\alpha _*\pi _1(X)=G$
, then
![]() $\alpha $
must factor as the composition of
$\alpha $
must factor as the composition of
![]() $\delta $
and a primitive cover of
$\delta $
and a primitive cover of
![]() $Y'$
. By results of Clebsch [Reference ClebschC1872], Fulton [Reference FultonF69], and Gabai–Kazez [Reference Gabai and KazezGK90] (see [Reference Coskun, Larson and VogtCLV22, Proposition 2.2]), the Hurwitz scheme parameterizing genus g degree
$Y'$
. By results of Clebsch [Reference ClebschC1872], Fulton [Reference FultonF69], and Gabai–Kazez [Reference Gabai and KazezGK90] (see [Reference Coskun, Larson and VogtCLV22, Proposition 2.2]), the Hurwitz scheme parameterizing genus g degree
![]() $r^{\text {pr}}$
primitive covers of
$r^{\text {pr}}$
primitive covers of
![]() $Y'$
is irreducible. We conclude that there is a bijection between irreducible components of
$Y'$
is irreducible. We conclude that there is a bijection between irreducible components of
![]() $\mathscr {H}_{r,g}$
and subgroups of
$\mathscr {H}_{r,g}$
and subgroups of
![]() $\pi _1(Y)$
of index dividing r.
$\pi _1(Y)$
of index dividing r.
2.3 The étale case
We briefly recall Beauville’s proof of Conjecture 1.1 [Reference BeauvilleB00, Proposition 4.1] in the étale case (see also the proof of [Reference Coskun, Larson and VogtCLV22, Proposition 1.3]).
First, we show that it suffices to consider the case of line bundles. Given a vector bundle V on X of degree d and rank s, let
![]() $\delta \colon Z \to X$
be an étale cover of degree s. If L is a line bundle of degree d on Z, then
$\delta \colon Z \to X$
be an étale cover of degree s. If L is a line bundle of degree d on Z, then
![]() $\delta _* L$
is a vector bundle of rank s and degree d on X. Hence, if we prove Conjecture 1.1 for (étale) maps in the case of line bundles, it follows for (étale) maps in higher rank as well.
$\delta _* L$
is a vector bundle of rank s and degree d on X. Hence, if we prove Conjecture 1.1 for (étale) maps in the case of line bundles, it follows for (étale) maps in higher rank as well.
Let
![]() $\alpha \colon X \to Y$
be étale, and let
$\alpha \colon X \to Y$
be étale, and let
![]() $\rho \colon Z \to Y$
be the Galois cover associated to
$\rho \colon Z \to Y$
be the Galois cover associated to
![]() $\alpha $
with Galois group G. Let
$\alpha $
with Galois group G. Let
![]() $\Sigma $
be the set of Y-morphisms
$\Sigma $
be the set of Y-morphisms
![]() $\sigma \colon Z \to X$
. Then
$\sigma \colon Z \to X$
. Then
The pullback by
![]() $\rho $
of any destabilizing subbundle of
$\rho $
of any destabilizing subbundle of
![]() $\alpha _* L$
would destabilize W. Hence,
$\alpha _* L$
would destabilize W. Hence,
![]() $\alpha _* L$
is semistable for every line bundle L on X.
$\alpha _* L$
is semistable for every line bundle L on X.
If
![]() $\alpha _* L$
has a proper subbundle F of the same slope as
$\alpha _* L$
has a proper subbundle F of the same slope as
![]() $\alpha _* L$
, then
$\alpha _* L$
, then
![]() $\rho ^* F$
is a G-invariant subbundle of W. Since the category of semistable bundles of a fixed slope is abelian with simple objects stable bundles,
$\rho ^* F$
is a G-invariant subbundle of W. Since the category of semistable bundles of a fixed slope is abelian with simple objects stable bundles,
![]() $\rho ^* F \cong \oplus _{\sigma \in \Sigma '} \sigma ^* L$
for some
$\rho ^* F \cong \oplus _{\sigma \in \Sigma '} \sigma ^* L$
for some
![]() $\Sigma ' \subset \Sigma $
. Since G acts transitively on
$\Sigma ' \subset \Sigma $
. Since G acts transitively on
![]() $\Sigma $
, it suffices to show that, if
$\Sigma $
, it suffices to show that, if
![]() $h>1$
and L is general, the line bundles
$h>1$
and L is general, the line bundles
![]() $\sigma ^*L$
are pairwise nonisomorphic as
$\sigma ^*L$
are pairwise nonisomorphic as
![]() $\sigma $
varies in
$\sigma $
varies in
![]() $\Sigma $
.
$\Sigma $
.
For any fixed
![]() $\sigma \in \Sigma '$
, let
$\sigma \in \Sigma '$
, let
![]() $H \subset G$
be the subgroup fixing
$H \subset G$
be the subgroup fixing
![]() $\sigma $
. The subvariety
$\sigma $
. The subvariety
![]() $\sigma ^*\operatorname {Pic}^dX \subset \operatorname {Pic} Z$
has dimension g, contains
$\sigma ^*\operatorname {Pic}^dX \subset \operatorname {Pic} Z$
has dimension g, contains
![]() $\sigma ^*L$
and is invariant under H. On the other hand, if
$\sigma ^*L$
and is invariant under H. On the other hand, if
![]() $\sigma ^*\operatorname {Pic}^d X$
is invariant under a subgroup
$\sigma ^*\operatorname {Pic}^d X$
is invariant under a subgroup
![]() $H'$
with
$H'$
with
![]() $H \subsetneq H' \subset G$
, then it would be pulled back from
$H \subsetneq H' \subset G$
, then it would be pulled back from
![]() $\operatorname {Pic} (Z/H')$
. By the Riemann–Hurwitz formula, the genus of
$\operatorname {Pic} (Z/H')$
. By the Riemann–Hurwitz formula, the genus of
![]() $Z/H'$
is strictly smaller than g. Hence, by dimension reasons, this containment is impossible and the
$Z/H'$
is strictly smaller than g. Hence, by dimension reasons, this containment is impossible and the
![]() $\sigma ^*L$
are pairwaise distinct. This shows the stability of
$\sigma ^*L$
are pairwaise distinct. This shows the stability of
![]() $\alpha _* L$
.
$\alpha _* L$
.
3 Proof of Theorem 1.2
Let Y be a curve of genus h, and let g be an integer such that
![]() $g> r(h - 1) + 1$
. Fix an étale cover
$g> r(h - 1) + 1$
. Fix an étale cover
![]() $\alpha ^{\text {\'et}} \colon Y' \to Y$
of degree
$\alpha ^{\text {\'et}} \colon Y' \to Y$
of degree
![]() $r^{\text {\'et}} \mid r$
. We first explain how to construct a nodal cover
$r^{\text {\'et}} \mid r$
. We first explain how to construct a nodal cover
![]() $\alpha _1 \colon X_1 \to Y$
of arithmetic genus g, whose primitive-étale factorization is
$\alpha _1 \colon X_1 \to Y$
of arithmetic genus g, whose primitive-étale factorization is
The first step of our construction is to fix a cyclic étale cover
![]() $\beta _0 \colon X_0 \to Y'$
of degree
$\beta _0 \colon X_0 \to Y'$
of degree
![]() $r^{\text {pr}} = r / r^{\text {\'et}}$
. Such covers correspond to points of order
$r^{\text {pr}} = r / r^{\text {\'et}}$
. Such covers correspond to points of order
![]() $r^{\text {pr}}$
in
$r^{\text {pr}}$
in
![]() $\text {Jac}(Y')$
, which always exist. Write
$\text {Jac}(Y')$
, which always exist. Write
![]() $\tau \colon X_0 \to X_0$
for the automorphism corresponding to the generator of
$\tau \colon X_0 \to X_0$
for the automorphism corresponding to the generator of
![]() $\mathbb {Z} / r^{\text {pr}} \mathbb {Z}$
. Let
$\mathbb {Z} / r^{\text {pr}} \mathbb {Z}$
. Let ![]() . We then pick general points
. We then pick general points
![]() $p_1, p_2, \ldots , p_{n} \in X_0$
, and let
$p_1, p_2, \ldots , p_{n} \in X_0$
, and let
![]() $p_i' = \tau (p_i)$
. Let
$p_i' = \tau (p_i)$
. Let
![]() $X_1$
be the curve obtained from
$X_1$
be the curve obtained from
![]() $X_0$
by gluing every
$X_0$
by gluing every
![]() $p_i$
to
$p_i$
to
![]() $p_i'$
for
$p_i'$
for
![]() $1 \leq i \leq n$
, and denote the normalization
$1 \leq i \leq n$
, and denote the normalization
![]() $ \nu \colon X_0 \to X_1$
. Let
$ \nu \colon X_0 \to X_1$
. Let
![]() $\beta _1 \colon X_1 \to Y'$
be the induced morphism, and let
$\beta _1 \colon X_1 \to Y'$
be the induced morphism, and let ![]() .
.
Proposition 3.1. The cover
![]() $\beta _1 \colon X_1 \to Y'$
is primitive.
$\beta _1 \colon X_1 \to Y'$
is primitive.
Proof. We must show that the pushforward
![]() $\pi _1(X_1) \to \pi _1(Y')$
is surjective. By [Reference SzamuelyS09, Proposition 5.5.4(2)], this is equivalent to the assertion that for all finite étale connected covers
$\pi _1(X_1) \to \pi _1(Y')$
is surjective. By [Reference SzamuelyS09, Proposition 5.5.4(2)], this is equivalent to the assertion that for all finite étale connected covers
![]() $Y" \to Y'$
, the fiber product
$Y" \to Y'$
, the fiber product
![]() $X_1 \times _{Y'} Y"$
is connected.
$X_1 \times _{Y'} Y"$
is connected.
Consider the dominant map
![]() $\epsilon \colon X_0 \times _{Y'} Y" \to X_1 \times _{Y'} Y"$
. By construction,
$\epsilon \colon X_0 \times _{Y'} Y" \to X_1 \times _{Y'} Y"$
. By construction,
![]() $\mathbb {Z}/r^{\text {pr}}\mathbb {Z}$
acts transitively on the components of
$\mathbb {Z}/r^{\text {pr}}\mathbb {Z}$
acts transitively on the components of
![]() $X_0 \times _{Y'} Y"$
. Therefore, it suffices to show that for any component
$X_0 \times _{Y'} Y"$
. Therefore, it suffices to show that for any component
![]() $Z \subset X_0 \times _{Y'} Y"$
, the components
$Z \subset X_0 \times _{Y'} Y"$
, the components
![]() $\epsilon (Z)$
and
$\epsilon (Z)$
and
![]() $\epsilon (\tau (Z))$
intersect. Since
$\epsilon (\tau (Z))$
intersect. Since
![]() $Z \to X_0$
is surjective, Z contains a point of the form
$Z \to X_0$
is surjective, Z contains a point of the form
![]() $(p_1, y")$
for some
$(p_1, y")$
for some
![]() $y" \in Y"$
and so
$y" \in Y"$
and so
![]() $\tau (Z)$
contains
$\tau (Z)$
contains
![]() $(p_1', y")$
. Since
$(p_1', y")$
. Since
![]() $\epsilon ((p_1, y")) = \epsilon ((p_1', y"))$
, the components
$\epsilon ((p_1, y")) = \epsilon ((p_1', y"))$
, the components
![]() $\epsilon (Z)$
and
$\epsilon (Z)$
and
![]() $\epsilon (\tau (Z))$
intersect as desired.
$\epsilon (\tau (Z))$
intersect as desired.
By the theory of formal patching (see [Reference LiuLi03, Lemma 5.6]), the map
![]() $\beta _1$
can be smoothed to a map
$\beta _1$
can be smoothed to a map
![]() $\beta \colon X \to Y'$
with a smooth domain X. Since being primitive is a deformation invariant, the resulting smoothing
$\beta \colon X \to Y'$
with a smooth domain X. Since being primitive is a deformation invariant, the resulting smoothing
![]() $\beta $
is also primitive by Proposition 3.1.
$\beta $
is also primitive by Proposition 3.1.
Proposition 3.2. Given a vector bundle V on
![]() $X_0$
, the pushforward
$X_0$
, the pushforward
![]() $\nu _*V$
to
$\nu _*V$
to
![]() $X_1$
is a limit of vector bundles of the same rank and slope
$X_1$
is a limit of vector bundles of the same rank and slope
![]() $\mu (V) + n$
on the smoothing X.
$\mu (V) + n$
on the smoothing X.
Proof. Let
![]() $\mathcal {X} \to \Delta $
denote a family of smooth curves specializing to
$\mathcal {X} \to \Delta $
denote a family of smooth curves specializing to
![]() $X_1$
with smooth total space. Consider the blowup at the nodes of
$X_1$
with smooth total space. Consider the blowup at the nodes of
![]() $X_1$
. In this family, the central fiber is the union of
$X_1$
. In this family, the central fiber is the union of
![]() $X_0$
together with n copies of
$X_0$
together with n copies of
![]() $\mathbb {P}^1$
, where each
$\mathbb {P}^1$
, where each
![]() $\mathbb {P}^1$
is attached at the two preimages of the corresponding node under the normalization map
$\mathbb {P}^1$
is attached at the two preimages of the corresponding node under the normalization map
![]() $\nu $
. These
$\nu $
. These
![]() $\mathbb {P}^1$
s appear with multiplicity 2 in the central fiber. Make a base change of order 2 and normalize the total space to obtain a family
$\mathbb {P}^1$
s appear with multiplicity 2 in the central fiber. Make a base change of order 2 and normalize the total space to obtain a family
![]() $ \mathcal {X}^+ \to \Delta '$
. This is a semistable family of smooth curves specializing to the union of
$ \mathcal {X}^+ \to \Delta '$
. This is a semistable family of smooth curves specializing to the union of
![]() $X_0$
with n copies of
$X_0$
with n copies of
![]() $\mathbb {P}^1$
, where now the central fiber
$\mathbb {P}^1$
, where now the central fiber
![]() $X^+$
is reduced. Write
$X^+$
is reduced. Write ![]() . The following diagram illustrates the maps that exist on the central fiber.
. The following diagram illustrates the maps that exist on the central fiber.

Let
![]() $V^+$
denote the vector bundle on
$V^+$
denote the vector bundle on
![]() $X^+$
obtained by gluing the vector bundle V on
$X^+$
obtained by gluing the vector bundle V on
![]() $X_0$
to
$X_0$
to
![]() $\mathcal {O}_{\mathbb {P}^1}(1)^{\oplus \operatorname {rk} V}$
on each
$\mathcal {O}_{\mathbb {P}^1}(1)^{\oplus \operatorname {rk} V}$
on each
![]() $\mathbb {P}^1$
component via any choice of gluing. (In fact the reader may check that any two choices result in isomorphic bundles.) Since V is locally free,
$\mathbb {P}^1$
component via any choice of gluing. (In fact the reader may check that any two choices result in isomorphic bundles.) Since V is locally free,
![]() $\mathscr {E}{\kern -1.5pt}xt^i(V^+, V^+) = 0$
for all
$\mathscr {E}{\kern -1.5pt}xt^i(V^+, V^+) = 0$
for all
![]() $i> 0$
. Thus, by the local-to-global
$i> 0$
. Thus, by the local-to-global
![]() $\operatorname {Ext}$
spectral sequence, we have that
$\operatorname {Ext}$
spectral sequence, we have that
![]() $\operatorname {Ext}_{X^+}^2(V^+, V^+) =0$
. By [Reference HartshorneH, Theorem 7.3 (b)], the obstructions to extending the bundle
$\operatorname {Ext}_{X^+}^2(V^+, V^+) =0$
. By [Reference HartshorneH, Theorem 7.3 (b)], the obstructions to extending the bundle
![]() $V^+$
to the whole family lie in
$V^+$
to the whole family lie in
![]() $\operatorname {Ext}_{X^+}^2(V^+, V^+)$
. Consequently,
$\operatorname {Ext}_{X^+}^2(V^+, V^+)$
. Consequently,
![]() $V^+$
extends to a vector bundle
$V^+$
extends to a vector bundle
![]() $\mathcal {V}^+$
on
$\mathcal {V}^+$
on
![]() $\mathcal {X}^+$
. Observe that
$\mathcal {X}^+$
. Observe that
![]() $\mathcal {V}^+$
has rank
$\mathcal {V}^+$
has rank
![]() $\operatorname {rk} V$
, and by the constancy of the Euler characteristic in flat families, the slope of the restriction of
$\operatorname {rk} V$
, and by the constancy of the Euler characteristic in flat families, the slope of the restriction of
![]() $\mathcal {V}^+$
to the fibers is
$\mathcal {V}^+$
to the fibers is
![]() $\mu (V^+)= \mu (V) + n$
.
$\mu (V^+)= \mu (V) + n$
.
Now, we claim that
![]() $\kappa _* \mathcal {V}^+|_{X_1} \simeq \nu _* V$
. Once we establish this claim, we obtain that
$\kappa _* \mathcal {V}^+|_{X_1} \simeq \nu _* V$
. Once we establish this claim, we obtain that
![]() $\nu _* V$
is the limit of vector bundles of the same rank and slope
$\nu _* V$
is the limit of vector bundles of the same rank and slope
![]() $\mu (V) + n$
on the smooth fibers.
$\mu (V) + n$
on the smooth fibers.
Let
![]() $(\operatorname {rk}, \chi )(F)$
denote the rank and Euler characteristic of a sheaf F, and write
$(\operatorname {rk}, \chi )(F)$
denote the rank and Euler characteristic of a sheaf F, and write
![]() $\mathcal {X}^{\prime }_t$
and
$\mathcal {X}^{\prime }_t$
and
![]() $\mathcal {X}^+_t$
for general fibers of their respective families. We first show that
$\mathcal {X}^+_t$
for general fibers of their respective families. We first show that
![]() $(\operatorname {rk}, \chi )(\kappa _* \mathcal {V}^+|_{X_1}) = (\operatorname {rk}, \chi )(\nu _*V)$
. By the constancy of the rank and the Euler characteristic in flat families and the fact that
$(\operatorname {rk}, \chi )(\kappa _* \mathcal {V}^+|_{X_1}) = (\operatorname {rk}, \chi )(\nu _*V)$
. By the constancy of the rank and the Euler characteristic in flat families and the fact that
![]() $\kappa $
is an isomorphism away from the central fiber, we have
$\kappa $
is an isomorphism away from the central fiber, we have
Furthermore, by considering the exact sequence for restriction to
![]() $X_0$
$X_0$
 $$\begin{align*}0 \to \bigoplus_{i=1}^n \mathcal{O}_{\mathbb{P}^1}(-1)^{\oplus \operatorname{rk}(V)} \to V^+ \to V^+|_{X_0} = V \to 0,\end{align*}$$
$$\begin{align*}0 \to \bigoplus_{i=1}^n \mathcal{O}_{\mathbb{P}^1}(-1)^{\oplus \operatorname{rk}(V)} \to V^+ \to V^+|_{X_0} = V \to 0,\end{align*}$$
we see that
![]() $(\operatorname {rk}, \chi )(V^+) = (\operatorname {rk}, \chi )(V)$
. Finally,
$(\operatorname {rk}, \chi )(V^+) = (\operatorname {rk}, \chi )(V)$
. Finally,
![]() $(\operatorname {rk}, \chi )(V) = (\operatorname {rk}, \chi )(\nu _*V)$
, which proves that
$(\operatorname {rk}, \chi )(V) = (\operatorname {rk}, \chi )(\nu _*V)$
, which proves that
![]() $(\operatorname {rk}, \chi )(\kappa _* \mathcal {V}^+|_{X_1}) = (\operatorname {rk}, \chi )(\nu _*V)$
.
$(\operatorname {rk}, \chi )(\kappa _* \mathcal {V}^+|_{X_1}) = (\operatorname {rk}, \chi )(\nu _*V)$
.
Hence, it suffices to construct a surjective map between
![]() $\kappa _* \mathcal {V}^+|_{X_1}$
and
$\kappa _* \mathcal {V}^+|_{X_1}$
and
![]() $\nu _* V$
. Consider the exact sequence on
$\nu _* V$
. Consider the exact sequence on
![]() $\mathcal {X}^+$
$\mathcal {X}^+$
Pushing forward under
![]() $\kappa $
, we obtain
$\kappa $
, we obtain
Observe that
![]() $\kappa _*(\mathcal {V}^+|_{X_0}) \simeq \nu _*V$
and that the map
$\kappa _*(\mathcal {V}^+|_{X_0}) \simeq \nu _*V$
and that the map
![]() $\kappa _*\mathcal {V}^+ \to \kappa _*(\mathcal {V}^+|_{X_0}) \simeq \nu _*V$
factors through
$\kappa _*\mathcal {V}^+ \to \kappa _*(\mathcal {V}^+|_{X_0}) \simeq \nu _*V$
factors through
![]() $(\kappa _*\mathcal {V}^+)|_{X_1}$
. Hence, it suffices to show that
$(\kappa _*\mathcal {V}^+)|_{X_1}$
. Hence, it suffices to show that
![]() $R^1\kappa _*\mathcal {V}^+(-X_0) = 0$
.
$R^1\kappa _*\mathcal {V}^+(-X_0) = 0$
.
Since
![]() $\kappa $
is an isomorphism away from the nodes of the
$\kappa $
is an isomorphism away from the nodes of the
![]() $X_1$
, the sheaf
$X_1$
, the sheaf
![]() $R^1\kappa _*\mathcal {V}^+(-X_0)$
is supported on the nodes of
$R^1\kappa _*\mathcal {V}^+(-X_0)$
is supported on the nodes of
![]() $X_1$
. It therefore suffices to show that its completion at every node p of
$X_1$
. It therefore suffices to show that its completion at every node p of
![]() $X_1$
vanishes. For this, we use the theorem on formal functions, which states that
$X_1$
vanishes. For this, we use the theorem on formal functions, which states that
where
![]() $\mathbb {P}^1 = \kappa ^{-1}(p)$
is a Cartier divisor on
$\mathbb {P}^1 = \kappa ^{-1}(p)$
is a Cartier divisor on
![]() $\mathcal {X}^+$
. It thus suffices to show that
$\mathcal {X}^+$
. It thus suffices to show that
![]() $H^1(\mathcal {V}^+(-X_0)|_{n \cdot \mathbb {P}^1})=0$
for all n. For this, we use induction on n, with base case
$H^1(\mathcal {V}^+(-X_0)|_{n \cdot \mathbb {P}^1})=0$
for all n. For this, we use induction on n, with base case
![]() $n=0$
, which is clear. For the inductive step, we use the exact sequence for restriction to
$n=0$
, which is clear. For the inductive step, we use the exact sequence for restriction to
![]() $n \cdot \mathbb {P}^1$
$n \cdot \mathbb {P}^1$
Since
![]() $\mathcal {V}^+(-X_0 - n \cdot \mathbb {P}^1)|_{\mathbb {P}^1} \simeq \mathcal {O}_{\mathbb {P}^1}(2n-1)^{\oplus \operatorname {rk} V}$
, which has vanishing
$\mathcal {V}^+(-X_0 - n \cdot \mathbb {P}^1)|_{\mathbb {P}^1} \simeq \mathcal {O}_{\mathbb {P}^1}(2n-1)^{\oplus \operatorname {rk} V}$
, which has vanishing
![]() $h^1$
, we conclude by induction that the middle term has vanishing
$h^1$
, we conclude by induction that the middle term has vanishing
![]() $h^1$
.
$h^1$
.
Proof of Theorem 1.2.
Let
![]() $\mathscr {H}$
be an irreducible component of the Hurwitz space
$\mathscr {H}$
be an irreducible component of the Hurwitz space
![]() $\mathscr {H}_{r, g}(Y)$
. Assume that the corresponding covers have primitive-étale factorization
$\mathscr {H}_{r, g}(Y)$
. Assume that the corresponding covers have primitive-étale factorization
Let
![]() $\beta _0 \colon X_0 \to Y'$
be the cyclic étale cover constructed above, and let
$\beta _0 \colon X_0 \to Y'$
be the cyclic étale cover constructed above, and let
be the cover constructed above by gluing points in the fibers of
![]() $\beta _0 \colon X_0 \to Y'$
.
$\beta _0 \colon X_0 \to Y'$
.
Let V be a general vector bundle on
![]() $X_0$
of arbitrary degree and rank. By [Reference BeauvilleB00, Proposition 4.1] (see §2.3), the pushforward
$X_0$
of arbitrary degree and rank. By [Reference BeauvilleB00, Proposition 4.1] (see §2.3), the pushforward
![]() ${\alpha _0}_*V$
is semistable if
${\alpha _0}_*V$
is semistable if
![]() $h=1$
and stable if
$h=1$
and stable if
![]() $h \geq 2$
. Since
$h \geq 2$
. Since
we conclude that
![]() ${\alpha _1}_* \nu _* V$
is semistable if
${\alpha _1}_* \nu _* V$
is semistable if
![]() $h=1$
and stable if
$h=1$
and stable if
![]() $h \geq 2$
.
$h \geq 2$
.
By Proposition 3.2, the pushforward bundle
![]() $\nu _*V$
on
$\nu _*V$
on
![]() $X_1$
is a limit of vector bundles on a smoothing
$X_1$
is a limit of vector bundles on a smoothing
![]() $X \to Y' \to Y$
and these vector bundles can be chosen to have any given degree and rank. The theorem follows by the openness of (semi)stability.
$X \to Y' \to Y$
and these vector bundles can be chosen to have any given degree and rank. The theorem follows by the openness of (semi)stability.
Acknowledgements
We would like to thank Arnaud Beauville, Anand Deopurkar, Aaron Landesman, Daniel Litt, Chien-Hao Liu, Anand Patel and Prof. Shing-Tung Yau for invaluable discussions. We thank the referee for their careful reading and useful suggestions. We are grateful to Mathematisches Forschungsinstitut Oberwolfach for providing an excellent work environment during the “Recent Trends in Algebraic Geometry” workshop in June 2023.
Competing interest
The authors have no competing interest to declare.
Funding statement
During the preparation of this article, I.C. was supported by NSF FRG grant DMS-1664296 and NSF grant DMS-2200684, E.L. was supported by NSF grants DMS-1802908 and DMS-2200641, and I.V. was supported by NSF grants DMS-1902743 and DMS-2200655.