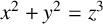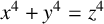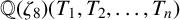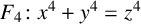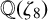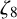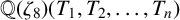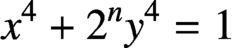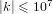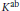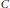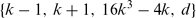Refine search
Actions for selected content:
18 results
THE FERMAT QUARTIC X4 + Y4 = 2m IN QUADRATIC NUMBER FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 15 August 2025, pp. 1-10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hilbert’s 10th problem via Mordell curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 26 February 2025, pp. 939-949
- Print publication:
- September 2025
-
- Article
- Export citation
FROBENIUS NUMBERS ASSOCIATED WITH DIOPHANTINE TRIPLES OF
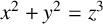 $x^2+y^2=z^3$
$x^2+y^2=z^3$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 14 November 2024, pp. 57-66
- Print publication:
- August 2025
-
- Article
- Export citation
POINTS ON
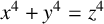 $x^4+y^4=z^4$ OVER QUADRATIC EXTENSIONS OF
$x^4+y^4=z^4$ OVER QUADRATIC EXTENSIONS OF 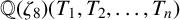 ${\mathbb {Q}}(\zeta _8)(T_1,T_2,\ldots ,T_n)$
${\mathbb {Q}}(\zeta _8)(T_1,T_2,\ldots ,T_n)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 07 November 2024, pp. 19-31
- Print publication:
- February 2025
-
- Article
- Export citation
How to solve a binary cubic equation in integers
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 07 March 2024, pp. 609-624
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Diagonal quartic surfaces with a Brauer–Manin obstruction
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 4 / April 2023
- Published online by Cambridge University Press:
- 17 March 2023, pp. 659-710
- Print publication:
- April 2023
-
- Article
- Export citation
COUNTEREXAMPLES TO THE HASSE PRINCIPLE IN FAMILIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 05 November 2021, pp. 18-27
- Print publication:
- August 2022
-
- Article
- Export citation
ON A PROBLEM OF RICHARD GUY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 13 September 2021, pp. 12-18
- Print publication:
- February 2022
-
- Article
- Export citation
A positive proportion of locally soluble quartic Thue equations are globally insoluble
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 05 August 2021, pp. 333-348
- Print publication:
- September 2022
-
- Article
- Export citation
THE DIOPHANTINE EQUATION
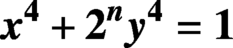 $\boldsymbol{x}^{\boldsymbol{4}} \boldsymbol{+} \boldsymbol{2}^{\boldsymbol{n}}\boldsymbol{y}^{\boldsymbol{4}} \boldsymbol{=} \boldsymbol{1}$ IN QUADRATIC NUMBER FIELDS
$\boldsymbol{x}^{\boldsymbol{4}} \boldsymbol{+} \boldsymbol{2}^{\boldsymbol{n}}\boldsymbol{y}^{\boldsymbol{4}} \boldsymbol{=} \boldsymbol{1}$ IN QUADRATIC NUMBER FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 06 November 2020, pp. 21-28
- Print publication:
- August 2021
-
- Article
- Export citation
Integral Points on Elliptic Curves and Explicit Valuations of Division Polynomials
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 5 / 01 October 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1120-1158
- Print publication:
- 01 October 2016
-
- Article
-
- You have access
- Export citation
Mordell’s equation: a classical approach
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 September 2015, pp. 633-646
-
- Article
-
- You have access
- Export citation
The Rank of Jacobian Varieties over the Maximal Abelian Extensions of Number Fields: Towards the Frey–Jarden Conjecture
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 4 / 01 December 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 842-849
- Print publication:
- 01 December 2012
-
- Article
-
- You have access
- Export citation
TWIN SQUAREFUL NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 93 / Issue 1-2 / October 2012
- Published online by Cambridge University Press:
- 19 September 2012, pp. 43-51
- Print publication:
- October 2012
-
- Article
-
- You have access
- Export citation
ON THE FAMILY OF DIOPHANTINE TRIPLES {k − 1, k + 1, 16k 3 − 4k}
-
- Journal:
- Glasgow Mathematical Journal / Volume 49 / Issue 2 / May 2007
- Published online by Cambridge University Press:
- 09 August 2007, pp. 333-344
- Print publication:
- May 2007
-
- Article
-
- You have access
- Export citation
ON A DIOPHANTINE EQUATION OF CASSELS
-
- Journal:
- Glasgow Mathematical Journal / Volume 47 / Issue 2 / May 2005
- Published online by Cambridge University Press:
- 27 July 2005, pp. 303-307
- Print publication:
- May 2005
-
- Article
-
- You have access
- Export citation
On the Unicity Conjecture for Markoff Numbers
-
- Journal:
- Canadian Mathematical Bulletin / Volume 39 / Issue 1 / 01 March 1996
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-9
- Print publication:
- 01 March 1996
-
- Article
-
- You have access
- Export citation
On Unit Solutions of the Equation xyz = x + y + z in Not Totally Real Cubic Fields
-
- Journal:
- Canadian Mathematical Bulletin / Volume 34 / Issue 1 / 01 March 1991
- Published online by Cambridge University Press:
- 20 November 2018, pp. 141-144
- Print publication:
- 01 March 1991
-
- Article
-
- You have access
- Export citation