No CrossRef data available.
Article contents
POINTS ON 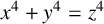 $x^4+y^4=z^4$ OVER QUADRATIC EXTENSIONS OF
$x^4+y^4=z^4$ OVER QUADRATIC EXTENSIONS OF 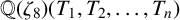 ${\mathbb {Q}}(\zeta _8)(T_1,T_2,\ldots ,T_n)$
${\mathbb {Q}}(\zeta _8)(T_1,T_2,\ldots ,T_n)$
Published online by Cambridge University Press: 07 November 2024
Abstract
Ishitsuka et al. [‘Explicit calculation of the mod 4 Galois representation associated with the Fermat quartic’, Int. J. Number Theory 16(4) (2020), 881–905] found all points on the Fermat quartic 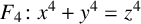 ${F_4\colon x^4+y^4=z^4}$ over quadratic extensions of
${F_4\colon x^4+y^4=z^4}$ over quadratic extensions of 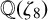 ${\mathbb {Q}}(\zeta _8)$, where
${\mathbb {Q}}(\zeta _8)$, where 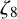 $\zeta _8$ is the eighth primitive root of unity
$\zeta _8$ is the eighth primitive root of unity 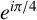 $e^{i\pi /4}$. Using Mordell’s technique, we give an alternative proof for the result of Ishitsuka et al. and extend it to the rational function field
$e^{i\pi /4}$. Using Mordell’s technique, we give an alternative proof for the result of Ishitsuka et al. and extend it to the rational function field 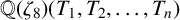 ${\mathbb {Q}}({\zeta _8})(T_1,T_2,\ldots ,T_n)$.
${\mathbb {Q}}({\zeta _8})(T_1,T_2,\ldots ,T_n)$.
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 111 , Issue 1 , February 2025 , pp. 19 - 31
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.
Footnotes
The author is supported by the Vietnam National Foundation for Science and Technology Development (NAFOSTED) (grant number 101.04-2023.21).
Dedicated to Professor Andrew Bremner


