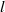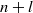Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Blomer, Valentin
and
Schöbel, Anita
2013.
Twins of powerful numbers.
Functiones et Approximatio Commentarii Mathematici,
Vol. 49,
Issue. 2,
Aktaş, Kevser
and
Ram Murty, M.
2017.
Fundamental units and consecutive squarefull numbers.
International Journal of Number Theory,
Vol. 13,
Issue. 01,
p.
243.