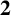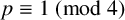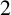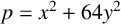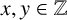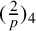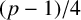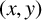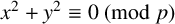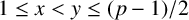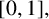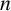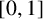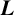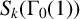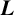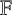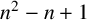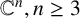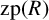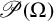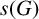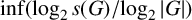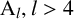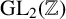Contents
Research Article
A NEW CHARACTERISATION FOR QUARTIC RESIDUACITY OF
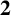 $\mathbf {2}$
$\mathbf {2}$
- Part of:
-
- Published online by Cambridge University Press:
- 14 March 2022, pp. 1-6
-
- Article
- Export citation
POINTS IN A FOLD
- Part of:
-
- Published online by Cambridge University Press:
- 10 January 2022, pp. 7-17
-
- Article
- Export citation
COUNTEREXAMPLES TO THE HASSE PRINCIPLE IN FAMILIES
- Part of:
-
- Published online by Cambridge University Press:
- 05 November 2021, pp. 18-27
-
- Article
- Export citation
COUNTING HECKE EIGENFORMS WITH NONVANISHING
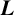 $\boldsymbol {L}$-VALUE
$\boldsymbol {L}$-VALUE
- Part of:
-
- Published online by Cambridge University Press:
- 24 January 2022, pp. 28-47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EULER PRODUCT ASYMPTOTICS FOR DIRICHLET
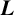 $\boldsymbol {L}$-FUNCTIONS
$\boldsymbol {L}$-FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 07 January 2022, pp. 48-56
-
- Article
- Export citation
PROOF OF SOME CONJECTURAL CONGRUENCES OF DA SILVA AND SELLERS
- Part of:
-
- Published online by Cambridge University Press:
- 13 December 2021, pp. 57-61
-
- Article
- Export citation
A NOTE ON GIRSTMAIR’S IRREDUCIBILITY CRITERION
- Part of:
-
- Published online by Cambridge University Press:
- 04 November 2021, pp. 62-66
-
- Article
- Export citation
AN EIGENVALUE CHARACTERISATION OF THE DUAL EDM CONE
- Part of:
-
- Published online by Cambridge University Press:
- 18 November 2021, pp. 67-69
-
- Article
- Export citation
MINIMALLY TRANSITIVE FAMILIES OF SUBSPACES OF
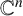 $\mathbb {C}^n$
$\mathbb {C}^n$
- Part of:
-
- Published online by Cambridge University Press:
- 20 January 2022, pp. 70-82
-
- Article
- Export citation
THE PROBABILITY OF ZERO MULTIPLICATION IN FINITE RINGS
- Part of:
-
- Published online by Cambridge University Press:
- 24 January 2022, pp. 83-88
-
- Article
- Export citation
THE NUMBER OF SET ORBITS OF PERMUTATION GROUPS AND THE GROUP ORDER
- Part of:
-
- Published online by Cambridge University Press:
- 27 January 2022, pp. 89-101
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AUTOMORPHISM AND OUTER AUTOMORPHISM GROUPS OF RIGHT-ANGLED ARTIN GROUPS ARE NOT RELATIVELY HYPERBOLIC
- Part of:
-
- Published online by Cambridge University Press:
- 24 January 2022, pp. 102-112
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON ÉTALE REPRESENTATIONS FROM NILPOTENT ORBITS
- Part of:
-
- Published online by Cambridge University Press:
- 25 January 2022, pp. 113-125
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PLANAR IMMERSIONS WITH PRESCRIBED CURL AND JACOBIAN DETERMINANT ARE UNIQUE
- Part of:
-
- Published online by Cambridge University Press:
- 08 October 2021, pp. 126-131
-
- Article
- Export citation
LI–YORKE CHAOS ALMOST EVERYWHERE: ON THE PERVASIVENESS OF DISJOINT EXTREMALLY SCRAMBLED SETS
- Part of:
-
- Published online by Cambridge University Press:
- 03 March 2022, pp. 132-143
-
- Article
- Export citation
RELATIVELY AMENABLE ACTIONS OF THOMPSON’S GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 03 November 2021, pp. 144-150
-
- Article
- Export citation
FINITE SUM OF COMPOSITION OPERATORS ON FOCK SPACE
- Part of:
-
- Published online by Cambridge University Press:
- 20 December 2021, pp. 151-162
-
- Article
- Export citation
Abstracts of Australasian PhD Theses
SOLUTIONS TO DIFFERENTIAL EQUATIONS VIA FIXED POINT APPROACHES: NEW MATHEMATICAL FOUNDATIONS AND APPLICATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 09 June 2022, pp. 163-164
-
- Article
-
- You have access
- HTML
- Export citation
PATTERN FORMATION IN ELECTRICALLY COUPLED PACEMAKER CELLS
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2022, pp. 165-166
-
- Article
-
- You have access
- HTML
- Export citation
TRANSVERSALITY, REGULARITY AND ERROR BOUNDS IN VARIATIONAL ANALYSIS AND OPTIMISATION
- Part of:
-
- Published online by Cambridge University Press:
- 09 June 2022, pp. 167-169
-
- Article
-
- You have access
- HTML
- Export citation