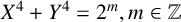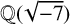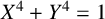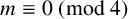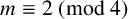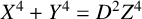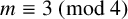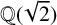1 Introduction
The Fermat quartic
![]() $x^4 + y^4 = 2^m$
was shown to have no nontrivial rational solutions for any integer m by Lebesgue [Reference Lebesgue6]. After Hilbert proved in his Zahlbericht [Reference Hilbert5, Theorem 169] that there are no solutions
$x^4 + y^4 = 2^m$
was shown to have no nontrivial rational solutions for any integer m by Lebesgue [Reference Lebesgue6]. After Hilbert proved in his Zahlbericht [Reference Hilbert5, Theorem 169] that there are no solutions
![]() $X, Y \in \mathbb {Q}(\sqrt {-1})$
of
$X, Y \in \mathbb {Q}(\sqrt {-1})$
of
![]() $X^4 + Y^4 = 1$
in the Gaussian field
$X^4 + Y^4 = 1$
in the Gaussian field
![]() $\mathbb {Q}(\sqrt {-1})$
, Aigner showed in 1934 that only in
$\mathbb {Q}(\sqrt {-1})$
, Aigner showed in 1934 that only in
![]() $\mathbb {Q}(\sqrt {-7})$
do quadratic solutions to
$\mathbb {Q}(\sqrt {-7})$
do quadratic solutions to
![]() $X^4 + Y^4 = 1$
exist [Reference Aigner1]. For instance,
$X^4 + Y^4 = 1$
exist [Reference Aigner1]. For instance,
 $$ \begin{align*}\bigg(\frac{1+\sqrt{-7}}{2}\bigg)^4+\bigg(\frac{1-\sqrt{-7}}{2}\bigg)^4=1.\end{align*} $$
$$ \begin{align*}\bigg(\frac{1+\sqrt{-7}}{2}\bigg)^4+\bigg(\frac{1-\sqrt{-7}}{2}\bigg)^4=1.\end{align*} $$
Faddeev in 1960 and Mordell in 1967 reproved this result [Reference Faddeev4, Reference Mordell8]. We adapt the method used by Mordell and classify the quadratic number fields that contain solutions to the Fermat quartic
![]() $X^4 + Y^4 = 2^m$
,
$X^4 + Y^4 = 2^m$
,
![]() $m \in \mathbb {Z}$
. Since a solution of
$m \in \mathbb {Z}$
. Since a solution of
![]() $X^4 + Y^4 = 2^m$
can be used to produce a solution to
$X^4 + Y^4 = 2^m$
can be used to produce a solution to
![]() $X^4 + Y^4 = 2^{m+4k}$
for any
$X^4 + Y^4 = 2^{m+4k}$
for any
![]() $k \in \mathbb {Z}$
, it is sufficient to restrict our discussion to
$k \in \mathbb {Z}$
, it is sufficient to restrict our discussion to
![]() $m = 1, 2, 3$
.
$m = 1, 2, 3$
.
Emory used the approach taken by Mordell in [Reference Mordell8] to determine all quadratic number fields that contain solutions to
![]() $X^4+Y^4=d^2$
[Reference Emory3]. She found that the equation
$X^4+Y^4=d^2$
[Reference Emory3]. She found that the equation
![]() ${X^4 + Y^4 = d^2}$
has nontrivial quadratic solutions precisely when
${X^4 + Y^4 = d^2}$
has nontrivial quadratic solutions precisely when
![]() $d = 1$
, or d is a congruent number, a positive integer that can be expressed as the area of a right triangle with rational sides. Since
$d = 1$
, or d is a congruent number, a positive integer that can be expressed as the area of a right triangle with rational sides. Since
![]() $2$
is not a congruent number [Reference Conrad2], there are no nontrivial quadratic solutions to
$2$
is not a congruent number [Reference Conrad2], there are no nontrivial quadratic solutions to
![]() $X^4 + Y^4 = 2^m$
for
$X^4 + Y^4 = 2^m$
for
![]() $m = 2$
. Of course, solutions such as
$m = 2$
. Of course, solutions such as
![]() $(X, Y) = (0, \sqrt {2})$
exist.
$(X, Y) = (0, \sqrt {2})$
exist.
Thus, in this paper, we restrict ourselves to the two cases
![]() $m=1$
and
$m=1$
and
![]() $m=3$
. For the remainder of this paper,
$m=3$
. For the remainder of this paper,
![]() $K=\mathbb {Q}(\sqrt {n})$
is a quadratic field with
$K=\mathbb {Q}(\sqrt {n})$
is a quadratic field with
![]() $n\in \mathbb {Z}$
squarefree. A trivial solution to the Fermat quartic
$n\in \mathbb {Z}$
squarefree. A trivial solution to the Fermat quartic
![]() $X^4 + Y^4 = 2^m$
occurs when
$X^4 + Y^4 = 2^m$
occurs when
![]() $XY = 0 $
or
$XY = 0 $
or
![]() ${X = \pm Y}$
. A quadratic solution
${X = \pm Y}$
. A quadratic solution
![]() $(X,Y)\in K\times K$
occurs when at least one of
$(X,Y)\in K\times K$
occurs when at least one of
![]() $X, Y$
is irrational. A quadratic conjugate pair
$X, Y$
is irrational. A quadratic conjugate pair
![]() $(X, Y)$
exists when
$(X, Y)$
exists when
![]() $X=a+b\sqrt {n}$
,
$X=a+b\sqrt {n}$
,
![]() $a,b\in \mathbb {Q}$
,
$a,b\in \mathbb {Q}$
,
![]() $ab\neq 0$
,
$ab\neq 0$
,
![]() $Y=\pm (a-b\sqrt {n})$
and
$Y=\pm (a-b\sqrt {n})$
and
![]() $X^4 + Y^4 = 2^m$
.
$X^4 + Y^4 = 2^m$
.
Theorem 1.1. Let K be a quadratic number field and let
![]() $(X, Y)\in K\times K$
be a quadratic solution of the Fermat quartic
$(X, Y)\in K\times K$
be a quadratic solution of the Fermat quartic
![]() $X^4+Y^4=2$
. Then, one of the following occurs:
$X^4+Y^4=2$
. Then, one of the following occurs:
-
(1)
 $X^4=Y^4$
and
$X^4=Y^4$
and
 $K=\mathbb {Q}(\sqrt {-1})$
—for instance,
$K=\mathbb {Q}(\sqrt {-1})$
—for instance,
 $(X,Y)=(1, \sqrt {-1})$
;
$(X,Y)=(1, \sqrt {-1})$
; -
(2)
 $X^4\neq Y^4$
and
$X^4\neq Y^4$
and
 $X^2, Y^2\in \mathbb {Q}$
—in this case,
$X^2, Y^2\in \mathbb {Q}$
—in this case,
 $(X,Y)$
generates a rational point
$(X,Y)$
generates a rational point
 $(a, b)$
on the elliptic curve
$(a, b)$
on the elliptic curve
 $y^2=x^3+8x$
;
$y^2=x^3+8x$
; -
(3)
 $X^4\neq Y^4$
and at least one of
$X^4\neq Y^4$
and at least one of
 $X^2$
,
$X^2$
,
 $Y^2$
is irrational. In this case,
$Y^2$
is irrational. In this case,
 $(X,Y)$
is necessarily a quadratic conjugate pair—indeed, neither of
$(X,Y)$
is necessarily a quadratic conjugate pair—indeed, neither of
 $X^2, Y^2$
is rational—and
$X^2, Y^2$
is rational—and
 $(X, Y)$
generates a rational point
$(X, Y)$
generates a rational point
 $(a, b)$
on the elliptic curve
$(a, b)$
on the elliptic curve
 $y^2 = x^3 - 2x$
.
$y^2 = x^3 - 2x$
.
Conversely, given a rational point
![]() $(a,b)\in \mathbb {Q}\times \mathbb {Q}$
on one of these two elliptic curves:
$(a,b)\in \mathbb {Q}\times \mathbb {Q}$
on one of these two elliptic curves:
-
(1) for
 $y^2 =x^3+8x$
, then
$y^2 =x^3+8x$
, then
 $K = \mathbb {Q}(\sqrt {2a^3 - 24a^2 - b^2 - 48b - 64})$
contains the K-point on
$K = \mathbb {Q}(\sqrt {2a^3 - 24a^2 - b^2 - 48b - 64})$
contains the K-point on
 $X^4 + Y^4 = 2$
,
$X^4 + Y^4 = 2$
,  $$ \begin{align*}(X, Y)=\bigg(\frac{4a+b-8}{2a+b+8},\frac{\sqrt{2a^3 - 24a^2-b^2-48b-64}}{2a+b+8}\bigg);\end{align*} $$
$$ \begin{align*}(X, Y)=\bigg(\frac{4a+b-8}{2a+b+8},\frac{\sqrt{2a^3 - 24a^2-b^2-48b-64}}{2a+b+8}\bigg);\end{align*} $$
-
(2) for
 $y^2=x^3-2x$
, then
$y^2=x^3-2x$
, then
 $K=\mathbb {Q}(\sqrt {-a^3 -3a^2 - 2a})$
contains the K-point on
$K=\mathbb {Q}(\sqrt {-a^3 -3a^2 - 2a})$
contains the K-point on
 $X^4+Y^4=2$
,
$X^4+Y^4=2$
,  $$ \begin{align*}(X, Y)=\bigg(\frac{a+\sqrt{-a^3 - 3a^2 - 2a}}{b},\frac{a-\sqrt{-a^3 - 3a^2 - 2a}}{b}\bigg).\end{align*} $$
$$ \begin{align*}(X, Y)=\bigg(\frac{a+\sqrt{-a^3 - 3a^2 - 2a}}{b},\frac{a-\sqrt{-a^3 - 3a^2 - 2a}}{b}\bigg).\end{align*} $$
Furthermore, each of these elliptic curves produces infinitely many different quadratic fields K that contain solutions to
![]() $X^4 + Y^4 = 2$
.
$X^4 + Y^4 = 2$
.
Theorem 1.2. Let K be a quadratic number field and let
![]() $(X, Y)\in K\times K$
be a quadratic solution of the Fermat quartic
$(X, Y)\in K\times K$
be a quadratic solution of the Fermat quartic
![]() $X^4+Y^4=8$
. Then, either:
$X^4+Y^4=8$
. Then, either:
-
(1)
 $K=\mathbb {Q}(\sqrt {2})$
with trivial solutions such as
$K=\mathbb {Q}(\sqrt {2})$
with trivial solutions such as
 $(X, Y)=(\sqrt {2},\sqrt {2})$
; or
$(X, Y)=(\sqrt {2},\sqrt {2})$
; or -
(2)
 $K=\mathbb {Q}(\sqrt {-2})$
with trivial solutions such as
$K=\mathbb {Q}(\sqrt {-2})$
with trivial solutions such as
 $(X, Y)=(\sqrt {-2},\sqrt {-2})$
.
$(X, Y)=(\sqrt {-2},\sqrt {-2})$
.
Remark 1.3. Quadratic solutions to
![]() $X^4 + Y^4 = 2$
arise from the infinitely many rational points on the two elliptic curves
$X^4 + Y^4 = 2$
arise from the infinitely many rational points on the two elliptic curves
![]() $y^2 = x^3 + 8x$
and
$y^2 = x^3 + 8x$
and
![]() $y^2 = x^3 - 2x$
, which belong to the same isogeny class with LMFDB label 256.b [11]. The isogenies are described in [Reference Silverman10, Ch. 3, Section 4]. Quadratic solutions to
$y^2 = x^3 - 2x$
, which belong to the same isogeny class with LMFDB label 256.b [11]. The isogenies are described in [Reference Silverman10, Ch. 3, Section 4]. Quadratic solutions to
![]() $X^4 + Y^4 = 8$
arise from the elliptic curve
$X^4 + Y^4 = 8$
arise from the elliptic curve
![]() $y^2 = x^3 - 8x$
, which has only one rational point, namely
$y^2 = x^3 - 8x$
, which has only one rational point, namely
![]() $(0, 0)$
. Thus, there are no nontrivial solutions to
$(0, 0)$
. Thus, there are no nontrivial solutions to
![]() $X^4 + Y^4 = 8$
.
$X^4 + Y^4 = 8$
.
In a slightly different direction, but still using Mordell’s approach, A. Li has determined the quadratic solutions to
![]() $X^4 + 2^mY^4 = 1$
[Reference Li7]. None of the solutions Li describes are quadratic conjugate pairs. Furthermore, although it is beyond the scope of this paper, we would be remiss if we did not point out that Faddeev and Mordell each also addressed the question of solutions to
$X^4 + 2^mY^4 = 1$
[Reference Li7]. None of the solutions Li describes are quadratic conjugate pairs. Furthermore, although it is beyond the scope of this paper, we would be remiss if we did not point out that Faddeev and Mordell each also addressed the question of solutions to
![]() $X^4 + Y^4 = 1$
within cubic number fields [Reference Faddeev4, Reference Mordell8], and that there continues to be work that examines Fermat quartics over algebraic number fields more generally, much of it using methods far beyond the scope of this paper. So that we do not expand our scope, we mention only [Reference Tho12] by N. X. Tho.
$X^4 + Y^4 = 1$
within cubic number fields [Reference Faddeev4, Reference Mordell8], and that there continues to be work that examines Fermat quartics over algebraic number fields more generally, much of it using methods far beyond the scope of this paper. So that we do not expand our scope, we mention only [Reference Tho12] by N. X. Tho.
We adopt the following convention: rationals are represented by lower case letters; generic elements of a quadratic field K are represented by upper case letters.
1.1 Outline and preliminary results
Let n be a squarefree integer,
![]() $K=\mathbb {Q}(\kern -1pt\sqrt {n})$
be a quadratic number field and suppose that
$K=\mathbb {Q}(\kern -1pt\sqrt {n})$
be a quadratic number field and suppose that
![]() $X, Y\in K$
satisfy
$X, Y\in K$
satisfy
We follow Mordell’s approach [Reference Mordell8], whose first step in addressing
![]() $X^4 + Y^4 = 1$
was to use the rational parametrisation of the unit circle, writing
$X^4 + Y^4 = 1$
was to use the rational parametrisation of the unit circle, writing
![]() $X^2$
and
$X^2$
and
![]() $Y^2$
in terms of a parameter T. Using this well-known parametrisation, and additionally noting that when m is odd, we have
$Y^2$
in terms of a parameter T. Using this well-known parametrisation, and additionally noting that when m is odd, we have
![]() $(X^2 - Y^2)^2 + (X^2 + Y^2)^2 = 2^{m+1}$
, we determine, for
$(X^2 - Y^2)^2 + (X^2 + Y^2)^2 = 2^{m+1}$
, we determine, for
![]() $X, Y\in K$
satisfying (1.1), that
$X, Y\in K$
satisfying (1.1), that
Solving for T yields
 $$ \begin{align}T = \frac{X^2 - Y^2}{2^{(m+1)/{2}} - (X^2 + Y^2)}\in K.\end{align} $$
$$ \begin{align}T = \frac{X^2 - Y^2}{2^{(m+1)/{2}} - (X^2 + Y^2)}\in K.\end{align} $$
Notice that
![]() $T\in \mathbb {Q}$
if and only if
$T\in \mathbb {Q}$
if and only if
![]() $(X^2,Y^2)\in \mathbb {Q}\times \mathbb {Q}$
, and
$(X^2,Y^2)\in \mathbb {Q}\times \mathbb {Q}$
, and
![]() $T = 0$
if and only if
$T = 0$
if and only if
![]() $X^2 = Y^2$
.
$X^2 = Y^2$
.
Following Mordell, our next step is to treat the two cases, T rational and T irrational, separately. When T is rational, our argument follows Mordell closely. However, in the second case, we find that
![]() $T\not \in \mathbb {Q}$
is not quite strong enough to follow Mordell. To follow Mordell’s approach, we need
$T\not \in \mathbb {Q}$
is not quite strong enough to follow Mordell. To follow Mordell’s approach, we need
![]() $T^2\not \in Q$
, but then we can continue with some necessary adjustments. The end result is that if
$T^2\not \in Q$
, but then we can continue with some necessary adjustments. The end result is that if
![]() $T^2\not \in Q$
, there are no quadratic solutions. This leaves the case
$T^2\not \in Q$
, there are no quadratic solutions. This leaves the case
![]() $T\not \in Q$
and
$T\not \in Q$
and
![]() $T^2\in Q$
, which implies that our quadratic solution is a quadratic conjugate pair. Thus, in our final result, we use an ad hoc approach to classify all quadratic conjugate pairs.
$T^2\in Q$
, which implies that our quadratic solution is a quadratic conjugate pair. Thus, in our final result, we use an ad hoc approach to classify all quadratic conjugate pairs.
2 Case T is rational
Adopt the notation in Section 1.1 and let
![]() $(X,Y)\in K \times K$
be a quadratic solution to
$(X,Y)\in K \times K$
be a quadratic solution to
![]() $X^4+Y^4=2^m$
,
$X^4+Y^4=2^m$
,
![]() $m=1,3$
. Suppose T is rational. Then, because of (1.2), we have
$m=1,3$
. Suppose T is rational. Then, because of (1.2), we have
![]() ${X^2, Y^2 \in \mathbb {Q}}$
. Note that for
${X^2, Y^2 \in \mathbb {Q}}$
. Note that for
![]() $a,b\in \mathbb {Q}$
,
$a,b\in \mathbb {Q}$
,
![]() $(a + b\sqrt {n})^2\in \mathbb {Q}$
implies that
$(a + b\sqrt {n})^2\in \mathbb {Q}$
implies that
![]() $ab= 0$
. Thus, setting
$ab= 0$
. Thus, setting
![]() $X=a+b\sqrt {n}$
and
$X=a+b\sqrt {n}$
and
![]() $Y = a_1 + b_1\sqrt {n}\in K$
, there are four cases:
$Y = a_1 + b_1\sqrt {n}\in K$
, there are four cases:
![]() $(X, Y) = (a,a_1), (a,b_1\sqrt {n}), (a\sqrt {n},b_1)$
or
$(X, Y) = (a,a_1), (a,b_1\sqrt {n}), (a\sqrt {n},b_1)$
or
![]() $(b\sqrt {n},b_1 \sqrt {n})$
, which we condense into two, that is,
$(b\sqrt {n},b_1 \sqrt {n})$
, which we condense into two, that is,
![]() ${X/Y \in \mathbb {Q}}$
or
${X/Y \in \mathbb {Q}}$
or
![]() $X/Y \not \in \mathbb {Q}$
.
$X/Y \not \in \mathbb {Q}$
.
Proposition 2.1. If
![]() $(X, Y) \in K \times K$
is a quadratic solution of
$(X, Y) \in K \times K$
is a quadratic solution of
![]() $X^4 + Y^4 = 2^m$
such that
$X^4 + Y^4 = 2^m$
such that
![]() $T \in \mathbb {Q}$
and
$T \in \mathbb {Q}$
and
![]() $X/Y \in \mathbb {Q}$
, then
$X/Y \in \mathbb {Q}$
, then
![]() $X^4 = Y^4$
. If
$X^4 = Y^4$
. If
![]() $(X, Y) \in K \times K$
is a quadratic solution of
$(X, Y) \in K \times K$
is a quadratic solution of
![]() ${X^4 + Y^4 = 2^m}$
such that
${X^4 + Y^4 = 2^m}$
such that
![]() $X^4 = Y^4$
, then
$X^4 = Y^4$
, then
![]() $K = \mathbb {Q}(\sqrt {-1})$
when
$K = \mathbb {Q}(\sqrt {-1})$
when
![]() $m = 1$
and
$m = 1$
and
![]() $K = \mathbb {Q}(\sqrt {2})$
or
$K = \mathbb {Q}(\sqrt {2})$
or
![]() $\mathbb {Q}(\sqrt {-2})$
when
$\mathbb {Q}(\sqrt {-2})$
when
![]() $m = 3$
.
$m = 3$
.
Proof. Let
![]() $X, Y$
satisfying
$X, Y$
satisfying
![]() $X^4+Y^4=2^m$
lie in a quadratic number field K. Suppose that
$X^4+Y^4=2^m$
lie in a quadratic number field K. Suppose that
![]() $T \in \mathbb {Q}$
and that
$T \in \mathbb {Q}$
and that
![]() $u = X/Y \in \mathbb {Q}$
. Then, using (1.2), we deduce that
$u = X/Y \in \mathbb {Q}$
. Then, using (1.2), we deduce that
![]() $u^2 {\kern-1.5pt}={\kern-1.5pt} (T^2 {\kern-1.5pt}+{\kern-1.5pt}2T-1)/ {(T^2 {\kern-1.5pt}-{\kern-1.5pt} 2T {\kern-1.5pt}-{\kern-1.5pt} 1)}$
. Setting
$u^2 {\kern-1.5pt}={\kern-1.5pt} (T^2 {\kern-1.5pt}+{\kern-1.5pt}2T-1)/ {(T^2 {\kern-1.5pt}-{\kern-1.5pt} 2T {\kern-1.5pt}-{\kern-1.5pt} 1)}$
. Setting
![]() $v {\kern-1.5pt}={\kern-1.5pt} u(T^2 {\kern-1.5pt}-{\kern-1.5pt} 2T {\kern-1.5pt}-{\kern-1.5pt} 1) {\kern-1.5pt}\in{\kern-1.5pt} \mathbb {Q}$
yields
$v {\kern-1.5pt}={\kern-1.5pt} u(T^2 {\kern-1.5pt}-{\kern-1.5pt} 2T {\kern-1.5pt}-{\kern-1.5pt} 1) {\kern-1.5pt}\in{\kern-1.5pt} \mathbb {Q}$
yields
![]() ${v^2 {\kern-1.5pt}={\kern-1.5pt} T^4 {\kern-1.5pt}-{\kern-1.5pt} 6T^2 {\kern-1.5pt}+{\kern-1.5pt} 1}$
, which is a curve with rational point
${v^2 {\kern-1.5pt}={\kern-1.5pt} T^4 {\kern-1.5pt}-{\kern-1.5pt} 6T^2 {\kern-1.5pt}+{\kern-1.5pt} 1}$
, which is a curve with rational point
![]() $(T, v) \in \mathbb {Q} \times \mathbb {Q}$
. Following the proof of [Reference Mordell9, Theorem 2 on page 77], we make a change of variables. First, we set
$(T, v) \in \mathbb {Q} \times \mathbb {Q}$
. Following the proof of [Reference Mordell9, Theorem 2 on page 77], we make a change of variables. First, we set
![]() ${v {\kern-1.5pt}={\kern-1.5pt} T^2 {\kern-1.5pt}-{\kern-1.5pt} 1 {\kern-1.5pt}-{\kern-1.5pt} 2x}$
. Note that
${v {\kern-1.5pt}={\kern-1.5pt} T^2 {\kern-1.5pt}-{\kern-1.5pt} 1 {\kern-1.5pt}-{\kern-1.5pt} 2x}$
. Note that
![]() $x \neq 1$
, because if
$x \neq 1$
, because if
![]() $x = 1$
, then we have
$x = 1$
, then we have
![]() $v = T^2 - 3$
, which would contradict
$v = T^2 - 3$
, which would contradict
![]() $v^2 = T^4 - 6T^2 + 1$
. Next, we set
$v^2 = T^4 - 6T^2 + 1$
. Next, we set
![]() $T = y / (1-x)$
. In this way, the point
$T = y / (1-x)$
. In this way, the point
![]() $(T, u) \in \mathbb {Q} \times \mathbb {Q}$
yields a rational point
$(T, u) \in \mathbb {Q} \times \mathbb {Q}$
yields a rational point
![]() $(x, y)$
with
$(x, y)$
with
![]() $x \neq 1$
on the elliptic curve
$x \neq 1$
on the elliptic curve
![]() $y^2 = x^3 - x$
, which has LMFDB label 32.a3 and Mordell–Weil group
$y^2 = x^3 - x$
, which has LMFDB label 32.a3 and Mordell–Weil group
![]() $\mathbb {Z}/2\mathbb {Z} \oplus \mathbb {Z}/2\mathbb {Z}$
. This elliptic curve has three rational points
$\mathbb {Z}/2\mathbb {Z} \oplus \mathbb {Z}/2\mathbb {Z}$
. This elliptic curve has three rational points
![]() $(0, 0), (1, 0), (-1, 0)$
, but only
$(0, 0), (1, 0), (-1, 0)$
, but only
![]() $(x, y) = (0, 0), (-1, 0)$
satisfy
$(x, y) = (0, 0), (-1, 0)$
satisfy
![]() $x \neq 1$
. Since
$x \neq 1$
. Since
![]() $y = 0$
in these two cases, we find that
$y = 0$
in these two cases, we find that
![]() $T = 0$
. Since
$T = 0$
. Since
![]() $T = 0$
, we have
$T = 0$
, we have
![]() $u^2 = 1$
, which means that
$u^2 = 1$
, which means that
![]() $X^2 = Y^2$
and thus
$X^2 = Y^2$
and thus
![]() $X^4 = Y^4$
.
$X^4 = Y^4$
.
Assume now that
![]() $X^4 = Y^4$
. Then,
$X^4 = Y^4$
. Then,
![]() $X^4 + Y^4 = 2$
reduces to
$X^4 + Y^4 = 2$
reduces to
![]() $X^4 = 1$
and thus
$X^4 = 1$
and thus
![]() ${K = \mathbb {Q}(\sqrt {-1})}$
. Similarly,
${K = \mathbb {Q}(\sqrt {-1})}$
. Similarly,
![]() $X^4 + Y^4 = 8$
reduces to
$X^4 + Y^4 = 8$
reduces to
![]() $X^4 = 4$
and thus
$X^4 = 4$
and thus
![]() $\mathbb {Q}(\sqrt {\pm 2})$
.
$\mathbb {Q}(\sqrt {\pm 2})$
.
Proposition 2.2. There exist infinitely many quadratic fields
![]() $K=\mathbb {Q}(\sqrt {n})$
that contain solutions
$K=\mathbb {Q}(\sqrt {n})$
that contain solutions
![]() $(X, Y)\in K\times K$
to the Fermat quartic
$(X, Y)\in K\times K$
to the Fermat quartic
![]() $X^4 + Y^4 = 2$
when
$X^4 + Y^4 = 2$
when
![]() $T\in \mathbb {Q}$
,
$T\in \mathbb {Q}$
,
![]() $X/Y\not \in \mathbb {Q}$
and
$X/Y\not \in \mathbb {Q}$
and
![]() $X^4 \neq Y^4$
. These solutions are derived from the infinitely many rational points on the elliptic curve
$X^4 \neq Y^4$
. These solutions are derived from the infinitely many rational points on the elliptic curve
![]() $y^2 = x^3 + 8x$
. For
$y^2 = x^3 + 8x$
. For
![]() $X^4 + Y^4 = 8$
, there exist no quadratic fields
$X^4 + Y^4 = 8$
, there exist no quadratic fields
![]() $K = \mathbb {Q}(\sqrt {n})$
that contain solutions
$K = \mathbb {Q}(\sqrt {n})$
that contain solutions
![]() $(X, Y) \in K\times K$
to the Fermat quartic
$(X, Y) \in K\times K$
to the Fermat quartic
![]() $X^4 + Y^4 = 8$
when
$X^4 + Y^4 = 8$
when
![]() $T \in \mathbb {Q}$
,
$T \in \mathbb {Q}$
,
![]() $X/Y \not \in \mathbb {Q}$
and
$X/Y \not \in \mathbb {Q}$
and
![]() $X^4 \neq Y^4$
.
$X^4 \neq Y^4$
.
Proof. We first begin with
![]() $m = 1$
and the curve
$m = 1$
and the curve
![]() $X^4 + Y^4 = 2$
. Without loss of generality,
$X^4 + Y^4 = 2$
. Without loss of generality,
![]() $(X, Y) = (a, b_1 \sqrt {n})$
and, thus,
$(X, Y) = (a, b_1 \sqrt {n})$
and, thus,
![]() $a^4 + b_1^4 n^2 = 2$
gives
$a^4 + b_1^4 n^2 = 2$
gives
![]() $j^2 + k^4 = 2$
. Notice that if
$j^2 + k^4 = 2$
. Notice that if
![]() $k = 1$
, then
$k = 1$
, then
![]() $j = \pm 1$
, which contradicts
$j = \pm 1$
, which contradicts
![]() $X^4 \neq Y^4$
. Thus,
$X^4 \neq Y^4$
. Thus,
![]() $k \neq 1$
, and using [Reference Mordell9, proof of Theorem 2 on page 77] and the solution
$k \neq 1$
, and using [Reference Mordell9, proof of Theorem 2 on page 77] and the solution
![]() $(j, k) = (1, 1)$
to
$(j, k) = (1, 1)$
to
![]() $j^2 + k^4 = 2$
, we make the change of variables
$j^2 + k^4 = 2$
, we make the change of variables
![]() $j = v(w+1)^{-2}$
,
$j = v(w+1)^{-2}$
,
![]() $k= 1 + (w+1)^{-1}$
, which yields
$k= 1 + (w+1)^{-1}$
, which yields
![]() $v^2 = w^4 - 12w^2 - 24w - 14$
. Since
$v^2 = w^4 - 12w^2 - 24w - 14$
. Since
![]() $k \neq 1$
, the rational point
$k \neq 1$
, the rational point
![]() $(j, k)$
produces a rational point
$(j, k)$
produces a rational point
![]() $(w, v) \in \mathbb {Q} \times \mathbb {Q}$
. We then set
$(w, v) \in \mathbb {Q} \times \mathbb {Q}$
. We then set
![]() $v = -w^2 +2h + 2$
to determine that
$v = -w^2 +2h + 2$
to determine that
Completing the square for the quadratic in w determines that
![]() $((h-2)w - 3)^2 = h^3 + h/2$
. Replacing
$((h-2)w - 3)^2 = h^3 + h/2$
. Replacing
![]() $(h-2)w - 3$
with
$(h-2)w - 3$
with
![]() $y/8$
and letting
$y/8$
and letting
![]() $x = 4h$
yields a rational point on the elliptic curve
$x = 4h$
yields a rational point on the elliptic curve
![]() $y^2 = x^3 + 8x$
with LMFDB label 256.b2, which has Mordell–Weil group
$y^2 = x^3 + 8x$
with LMFDB label 256.b2, which has Mordell–Weil group
![]() $\mathbb {Z} \oplus \mathbb {Z}/2\mathbb {Z}$
with the point
$\mathbb {Z} \oplus \mathbb {Z}/2\mathbb {Z}$
with the point
![]() $(1, 3)$
of infinite order.
$(1, 3)$
of infinite order.
Working backwards from any rational point
![]() $(a, b)\neq (8,-24)$
on the elliptic curve
$(a, b)\neq (8,-24)$
on the elliptic curve
![]() $y^2 = x^3 + 8x$
to our curve
$y^2 = x^3 + 8x$
to our curve
![]() $X^4 + Y^4 = 2$
yields the solution
$X^4 + Y^4 = 2$
yields the solution
 $$ \begin{align*}\bigg(\frac{4a+b-8}{2a+b+8} \bigg)^4 + \bigg(\frac{\sqrt{2a^3-24a^2-b^2 - 48b - 64}}{2a+b+8} \bigg)^4 = 2\end{align*} $$
$$ \begin{align*}\bigg(\frac{4a+b-8}{2a+b+8} \bigg)^4 + \bigg(\frac{\sqrt{2a^3-24a^2-b^2 - 48b - 64}}{2a+b+8} \bigg)^4 = 2\end{align*} $$
in the field
![]() $K=\mathbb {Q} (\sqrt {2a^3 - 24a^2 - b^2 - 48b-64})$
. This field is quadratic, namely
$K=\mathbb {Q} (\sqrt {2a^3 - 24a^2 - b^2 - 48b-64})$
. This field is quadratic, namely
![]() ${K\neq \mathbb {Q}}$
, for every rational point
${K\neq \mathbb {Q}}$
, for every rational point
![]() $(a,b)$
on
$(a,b)$
on
![]() $y^2 = x^3 + 8x$
with the exception of
$y^2 = x^3 + 8x$
with the exception of
![]() $(a,b)=(1,-3)$
. Note that for
$(a,b)=(1,-3)$
. Note that for
![]() $(a,b)=(1,-3)$
, we have
$(a,b)=(1,-3)$
, we have
![]() $2a^3 - 24a^2 - b^2 -48b-64=49$
and thus
$2a^3 - 24a^2 - b^2 -48b-64=49$
and thus
![]() ${K = \mathbb {Q}}$
. To prove this field is otherwise quadratic, we use the fact that, as Lebesgue proved,
${K = \mathbb {Q}}$
. To prove this field is otherwise quadratic, we use the fact that, as Lebesgue proved,
![]() $(X, Y)=(\pm 1,\pm 1)$
are the only rational solutions to
$(X, Y)=(\pm 1,\pm 1)$
are the only rational solutions to
![]() $X^4 + Y^4 = 2$
. Set
$X^4 + Y^4 = 2$
. Set
 $$ \begin{align*} A(x,y) = \frac{4x+ y - 8}{2x + y+ 8}, \quad B(x,y) = \frac{\sqrt{2x^3 - 24x^2 - y^2 - 48y - 64}}{2x + y + 8}. \end{align*} $$
$$ \begin{align*} A(x,y) = \frac{4x+ y - 8}{2x + y+ 8}, \quad B(x,y) = \frac{\sqrt{2x^3 - 24x^2 - y^2 - 48y - 64}}{2x + y + 8}. \end{align*} $$
Suppose that
![]() $B(a,b)$
is rational. This makes
$B(a,b)$
is rational. This makes
![]() $(A(a, b),B(a,b))$
a rational point on
$(A(a, b),B(a,b))$
a rational point on
![]() $X^4 + Y^4 = 2$
. Thus,
$X^4 + Y^4 = 2$
. Thus,
![]() $A(a,b)=\pm 1$
which, using
$A(a,b)=\pm 1$
which, using
![]() $y^2=x^3+8x$
, means that
$y^2=x^3+8x$
, means that
![]() $(a,b)=(0,0), (1,-3), (8,24)$
. Recall that the point
$(a,b)=(0,0), (1,-3), (8,24)$
. Recall that the point
![]() $(8,-24)$
was excluded. A quick calculation shows that
$(8,-24)$
was excluded. A quick calculation shows that
![]() $B(a,b)\neq \pm 1$
for
$B(a,b)\neq \pm 1$
for
![]() $(a,b)=(0,0)$
and
$(a,b)=(0,0)$
and
![]() $(a, b) = (8,24)$
. We record that
$(a, b) = (8,24)$
. We record that
![]() $(A(1,-3),B(1,-3))=(-1,1)$
.
$(A(1,-3),B(1,-3))=(-1,1)$
.
We now use Falting’s theorem and the fact that the Fermat quartic
![]() ${X^4+Y^4=2}$
is a nonsingular curve of genus 3 to prove there are infinitely many different quadratic fields
${X^4+Y^4=2}$
is a nonsingular curve of genus 3 to prove there are infinitely many different quadratic fields
![]() $\mathbb {Q}(\sqrt {2a^3 - 24a^2 -b^2 - 48b-64}) \not = \mathbb {Q}$
, where
$\mathbb {Q}(\sqrt {2a^3 - 24a^2 -b^2 - 48b-64}) \not = \mathbb {Q}$
, where
![]() $(a, b)$
is a rational point on
$(a, b)$
is a rational point on
![]() ${y^2 = x^3 + 8x}$
. Since each quadratic field K contains only finitely many solutions to
${y^2 = x^3 + 8x}$
. Since each quadratic field K contains only finitely many solutions to
![]() ${X^4+Y^4=2}$
, this will follow once we establish the fact that there are infinitely many different complex ordered pairs
${X^4+Y^4=2}$
, this will follow once we establish the fact that there are infinitely many different complex ordered pairs
![]() $(A(a,b),B(a, b))\in \mathbb {C}\times \mathbb {C}$
.
$(A(a,b),B(a, b))\in \mathbb {C}\times \mathbb {C}$
.
Since
![]() $A(a,b)\in \mathbb {Q}$
and
$A(a,b)\in \mathbb {Q}$
and
![]() $B(a_1,b_1)\not \in \mathbb {Q}$
for all rational points
$B(a_1,b_1)\not \in \mathbb {Q}$
for all rational points
![]() $(a_1, b_1)$
on
$(a_1, b_1)$
on
![]() ${y^2 = x^3 + 8x}$
except
${y^2 = x^3 + 8x}$
except
![]() $(a_1, b_1)=(1,-3)$
, there is no possibility of
$(a_1, b_1)=(1,-3)$
, there is no possibility of
![]() $A(a,b)=B(a_1,b_1)$
unless
$A(a,b)=B(a_1,b_1)$
unless
![]() ${B(a_1,b_1)=1}$
. If
${B(a_1,b_1)=1}$
. If
![]() $B(a_1,b_1)=1$
, then
$B(a_1,b_1)=1$
, then
![]() $A(a_1,b_1)=\pm 1$
since
$A(a_1,b_1)=\pm 1$
since
![]() $A(a_1,b_1)$
is rational. Recall that we have already described the finitely many points
$A(a_1,b_1)$
is rational. Recall that we have already described the finitely many points
![]() $(a_1, b_1)$
on
$(a_1, b_1)$
on
![]() $y^2=x^3+8x$
such that
$y^2=x^3+8x$
such that
![]() $A(a_1, b_1)=\pm 1$
. Thus, we focus on proving there are infinitely many different ordered pairs
$A(a_1, b_1)=\pm 1$
. Thus, we focus on proving there are infinitely many different ordered pairs
![]() $(A(a, b),B(a,b))\in \mathbb {C}\times \mathbb {C}\setminus \{(\pm 1,1)\}$
.
$(A(a, b),B(a,b))\in \mathbb {C}\times \mathbb {C}\setminus \{(\pm 1,1)\}$
.
Our only concern is the possibility that there might be infinitely many rational points
![]() $(a_i, b_i)$
on
$(a_i, b_i)$
on
![]() $y^2 = x^3 + 8x$
such that
$y^2 = x^3 + 8x$
such that
![]() $(A(a_i,b_i),B(a_i,b_i))=(A(a_j,b_j),B(a_j,b_j))\not \in \{(\pm 1,1)\}$
. If this were the case, letting
$(A(a_i,b_i),B(a_i,b_i))=(A(a_j,b_j),B(a_j,b_j))\not \in \{(\pm 1,1)\}$
. If this were the case, letting
![]() $k=A(a_i,b_i)\in \mathbb {Q}$
be the common value of the
$k=A(a_i,b_i)\in \mathbb {Q}$
be the common value of the
![]() $A(a_i,b_i)$
, we would have infinitely many intersections of
$A(a_i,b_i)$
, we would have infinitely many intersections of
![]() $y^2 = x^3 + 8x$
with the level curve
$y^2 = x^3 + 8x$
with the level curve
 $$ \begin{align*}k=\frac{4x+y-8}{2x+y+8}.\end{align*} $$
$$ \begin{align*}k=\frac{4x+y-8}{2x+y+8}.\end{align*} $$
Recall that since
![]() $(A(a,b),B(a,b))\not \in \{(\pm 1,1)\}$
, we have
$(A(a,b),B(a,b))\not \in \{(\pm 1,1)\}$
, we have
![]() $k\neq \pm 1$
. Since
$k\neq \pm 1$
. Since
![]() $k\neq 1$
, we may solve for y in the equation for the level curve and then use this to substitute for y in
$k\neq 1$
, we may solve for y in the equation for the level curve and then use this to substitute for y in
![]() $y^2 = x^3 + 8x$
. The result is a cubic equation in x with no more than three rational roots. As a result, the infinitely many rational points on
$y^2 = x^3 + 8x$
. The result is a cubic equation in x with no more than three rational roots. As a result, the infinitely many rational points on
![]() $y^2 = x^3 + 8x$
produce infinitely many different quadratic extensions K.
$y^2 = x^3 + 8x$
produce infinitely many different quadratic extensions K.
We now consider the case
![]() $m = 3$
and the curve
$m = 3$
and the curve
![]() $X^4 + Y^4 = 8$
. Again without loss of generality, we have
$X^4 + Y^4 = 8$
. Again without loss of generality, we have
![]() $(X, Y) = (a, b_1\sqrt {n})$
with
$(X, Y) = (a, b_1\sqrt {n})$
with
![]() $a,b_1\in \mathbb {Q}$
. Then,
$a,b_1\in \mathbb {Q}$
. Then,
![]() $a^4 + b_1^4 n^2 = 8$
and thus a nontrivial integer solution for
$a^4 + b_1^4 n^2 = 8$
and thus a nontrivial integer solution for
![]() $8x^4 - y^4 = z^2$
. However, this curve is known to have no nontrivial integer solutions by Lebesgue [Reference Lebesgue6] using the method of infinite descent, and thus there are no nontrivial quadratic fields that come out of this case.
$8x^4 - y^4 = z^2$
. However, this curve is known to have no nontrivial integer solutions by Lebesgue [Reference Lebesgue6] using the method of infinite descent, and thus there are no nontrivial quadratic fields that come out of this case.
Example 2.3. Taking the point
![]() $(a, b) = (1, 3)$
, which is a generator of the elliptic curve
$(a, b) = (1, 3)$
, which is a generator of the elliptic curve
![]() $y^2 = x^3 + 8x$
, gives the quadratic field
$y^2 = x^3 + 8x$
, gives the quadratic field
![]() $\mathbb {Q}(\sqrt {-239})$
with solution
$\mathbb {Q}(\sqrt {-239})$
with solution
 $$ \begin{align*}\bigg(-\frac{1}{13} \bigg)^4 + \bigg( \frac{\sqrt{-239}}{13}\bigg) ^4 = 2.\end{align*} $$
$$ \begin{align*}\bigg(-\frac{1}{13} \bigg)^4 + \bigg( \frac{\sqrt{-239}}{13}\bigg) ^4 = 2.\end{align*} $$
Example 2.4. Doubling the generator
![]() $(1, 3)$
under the group law of the elliptic curve
$(1, 3)$
under the group law of the elliptic curve
![]() $y^2 = x^3 + 8x$
yields the point
$y^2 = x^3 + 8x$
yields the point
![]() $(a, b) = (49/36, -791/216)$
. Using this point gives the quadratic field
$(a, b) = (49/36, -791/216)$
. Using this point gives the quadratic field
![]() $\mathbb {Q}(\sqrt {2750257})$
with solution
$\mathbb {Q}(\sqrt {2750257})$
with solution
 $$ \begin{align*}\bigg(-\frac{1343}{1525} \bigg)^4 + \bigg( \frac{\sqrt{2750257}}{1525} \bigg)^4 = 2.\end{align*} $$
$$ \begin{align*}\bigg(-\frac{1343}{1525} \bigg)^4 + \bigg( \frac{\sqrt{2750257}}{1525} \bigg)^4 = 2.\end{align*} $$
3 Case T is irrational
Adopt the notation in Section 1.1 and let
![]() $(X,Y)\in K\times K$
be a quadratic solution to
$(X,Y)\in K\times K$
be a quadratic solution to
![]() $X^4+Y^4=2^m$
,
$X^4+Y^4=2^m$
,
![]() $m=1,3$
. In this section, we prove two results. In the first result, we use an argument modelled after Mordell to prove that there are no quadratic solutions under the assumption that
$m=1,3$
. In this section, we prove two results. In the first result, we use an argument modelled after Mordell to prove that there are no quadratic solutions under the assumption that
![]() $T^2\not \in \mathbb {Q}$
. As a result, we assume
$T^2\not \in \mathbb {Q}$
. As a result, we assume
![]() $T^2 \in \mathbb {Q}$
and since
$T^2 \in \mathbb {Q}$
and since
![]() $(X, Y) \in K \times K$
with
$(X, Y) \in K \times K$
with
![]() $T \not \in \mathbb {Q}$
, we conclude that
$T \not \in \mathbb {Q}$
, we conclude that
![]() $(X, Y)$
is a quadratic conjugate pair. The second result uses the fact that
$(X, Y)$
is a quadratic conjugate pair. The second result uses the fact that
![]() $(X, Y)$
is a quadratic conjugate pair on the Fermat quartic
$(X, Y)$
is a quadratic conjugate pair on the Fermat quartic
![]() $X^4 + Y^4 = 2^m$
to produce a rational point on the elliptic curve
$X^4 + Y^4 = 2^m$
to produce a rational point on the elliptic curve
![]() $y^2 = x^3 - 2^mx$
.
$y^2 = x^3 - 2^mx$
.
Proposition 3.1. Let
![]() $K=\mathbb {Q}(\sqrt {n})$
with
$K=\mathbb {Q}(\sqrt {n})$
with
![]() $n\in \mathbb {Z}$
squarefree, and let
$n\in \mathbb {Z}$
squarefree, and let
![]() $(X,Y)\in K\times K$
be a quadratic solution to the Fermat quartic
$(X,Y)\in K\times K$
be a quadratic solution to the Fermat quartic
![]() $X^4+Y^4=2^m$
,
$X^4+Y^4=2^m$
,
![]() $m=1,3$
. If T, as defined by (1.3), is irrational, then
$m=1,3$
. If T, as defined by (1.3), is irrational, then
![]() $(X, Y)$
is a quadratic conjugate pair.
$(X, Y)$
is a quadratic conjugate pair.
Proof. We begin by supposing that
![]() $T\not \in \mathbb {Q}$
and
$T\not \in \mathbb {Q}$
and
![]() $T^2\in \mathbb {Q}$
. Thus, we have
$T^2\in \mathbb {Q}$
. Thus, we have
![]() $T = r\sqrt {n}\not \in \mathbb {Q}$
for some nonzero
$T = r\sqrt {n}\not \in \mathbb {Q}$
for some nonzero
![]() $r\in \mathbb {Q}$
. Using (1.2), this means that
$r\in \mathbb {Q}$
. Using (1.2), this means that
![]() $\sigma (X^2)=Y^2$
, where
$\sigma (X^2)=Y^2$
, where
![]() $\sigma :K\rightarrow K$
denotes conjugation. Since
$\sigma :K\rightarrow K$
denotes conjugation. Since
![]() $\sigma $
is a multiplicative homomorphism,
$\sigma $
is a multiplicative homomorphism,
![]() $\sigma (X)^2=Y^2$
, which means that
$\sigma (X)^2=Y^2$
, which means that
![]() $Y=\pm \sigma (X)$
and
$Y=\pm \sigma (X)$
and
![]() $(X, Y)$
is a quadratic conjugate pair.
$(X, Y)$
is a quadratic conjugate pair.
Now, we derive contradictions in the more complicated case in which
![]() $T^2\not \in \mathbb {Q}$
. Following the argument Mordell used in [Reference Mordell8], set
$T^2\not \in \mathbb {Q}$
. Following the argument Mordell used in [Reference Mordell8], set
![]() $Z = (1+T^2)XY \in K$
. Using (1.2), we find that
$Z = (1+T^2)XY \in K$
. Using (1.2), we find that
![]() $Z^2 = 2^{m-1}(T^4 - 6T^2 + 1)$
. Set
$Z^2 = 2^{m-1}(T^4 - 6T^2 + 1)$
. Set
![]() $V = Z/(2^{(m-1)/2}) - T^2 + 3 \in K$
. Since
$V = Z/(2^{(m-1)/2}) - T^2 + 3 \in K$
. Since
![]() $Z = 2^{(m-1)/2} (V + T^2 -3)$
, we have
$Z = 2^{(m-1)/2} (V + T^2 -3)$
, we have
![]() $V^2 + 2VT^2 - 6V + 8 = 0$
. If
$V^2 + 2VT^2 - 6V + 8 = 0$
. If
![]() $V \in \mathbb {Q}$
, then because
$V \in \mathbb {Q}$
, then because
![]() $V^2 + 2VT^2 - 6V + 8 = 0$
, we have
$V^2 + 2VT^2 - 6V + 8 = 0$
, we have
![]() $T^2 \in \mathbb {Q}$
, which is a contradiction. Thus,
$T^2 \in \mathbb {Q}$
, which is a contradiction. Thus,
![]() $V \not \in \mathbb {Q}$
, and there exist
$V \not \in \mathbb {Q}$
, and there exist
![]() $c, d\in \mathbb {Q}$
with
$c, d\in \mathbb {Q}$
with
![]() $d \neq 0$
such that
$d \neq 0$
such that
![]() $V = c+dT$
. Define the linear polynomial
$V = c+dT$
. Define the linear polynomial
![]() ${V(z) = c + dz \in \mathbb {Q}{[z]}}$
and observe that the polynomial
${V(z) = c + dz \in \mathbb {Q}{[z]}}$
and observe that the polynomial
has T as a root. Since
![]() $d \neq 0$
, this polynomial is cubic, which means that
$d \neq 0$
, this polynomial is cubic, which means that
![]() ${p(z) = F(z) G(z)}$
, where
${p(z) = F(z) G(z)}$
, where
![]() $F(z) \in \mathbb {Q}{[z]}$
is the monic irreducible quadratic polynomial for T and
$F(z) \in \mathbb {Q}{[z]}$
is the monic irreducible quadratic polynomial for T and
![]() ${G(z) \in \mathbb {Q}[z]}$
is linear. At this point,
${G(z) \in \mathbb {Q}[z]}$
is linear. At this point,
Since
![]() $G(z)$
is linear, it has a rational root e, which means that
$G(z)$
is linear, it has a rational root e, which means that
![]() $(x, y) = (e, V(e))$
is a rational point on the curve
$(x, y) = (e, V(e))$
is a rational point on the curve
![]() $y^2 + 2x^2y - 6y + 8 = 0$
. This elliptic curve has minimal Weierstrass equation
$y^2 + 2x^2y - 6y + 8 = 0$
. This elliptic curve has minimal Weierstrass equation
![]() $y^2 = x^3 - x$
with LMFDB label 32.a3 and Mordell–Weil group
$y^2 = x^3 - x$
with LMFDB label 32.a3 and Mordell–Weil group
![]() $\mathbb {Z}/2\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
. The four rational projective points on
$\mathbb {Z}/2\mathbb {Z}\oplus \mathbb {Z}/2\mathbb {Z}$
. The four rational projective points on
![]() $y^2z + 2x^2y - 6yz^2 + 8z^3 = 0$
are
$y^2z + 2x^2y - 6yz^2 + 8z^3 = 0$
are
![]() $(x : y : z)=(0: 1:0), (0:2:1), (0:4:1)$
and
$(x : y : z)=(0: 1:0), (0:2:1), (0:4:1)$
and
![]() $(1:0:0)$
. Thus, we determine that either
$(1:0:0)$
. Thus, we determine that either
![]() $(e, V(e)) = (0, 2)$
or
$(e, V(e)) = (0, 2)$
or
![]() $(e, V(e)) =(0, 4)$
. In both of these cases, the root of the linear polynomial
$(e, V(e)) =(0, 4)$
. In both of these cases, the root of the linear polynomial
![]() $Q(z) $
is
$Q(z) $
is
![]() $0$
; therefore,
$0$
; therefore,
![]() $G(z) = hz$
for some
$G(z) = hz$
for some
![]() $h \in \mathbb {Q}$
. Thus, (3.1) becomes
$h \in \mathbb {Q}$
. Thus, (3.1) becomes
![]() $(c+dz)^2 + 2(c +dz)z^2 - 6(c+dz) + 8 = F(z)hz.$
Comparing the leading terms, we see that
$(c+dz)^2 + 2(c +dz)z^2 - 6(c+dz) + 8 = F(z)hz.$
Comparing the leading terms, we see that
![]() $h=2d$
. Comparing the constant terms, we see that
$h=2d$
. Comparing the constant terms, we see that
![]() $c^2 - 6c + 8 = 0$
. Thus,
$c^2 - 6c + 8 = 0$
. Thus,
![]() $c = 2$
or
$c = 2$
or
![]() $4$
, and solving for
$4$
, and solving for
![]() $F(z)$
, we find that
$F(z)$
, we find that
which means that
 $$ \begin{align} T=\frac{-d^2-2c\pm\sqrt{d^4+(48-12c)d^2+4c^2}}{4d}.\end{align} $$
$$ \begin{align} T=\frac{-d^2-2c\pm\sqrt{d^4+(48-12c)d^2+4c^2}}{4d}.\end{align} $$
There are two cases
![]() $c = 2$
and
$c = 2$
and
![]() $c = 4$
to consider. For
$c = 4$
to consider. For
![]() $c=2$
, substituting T into (1.2) yields
$c=2$
, substituting T into (1.2) yields
 $$ \begin{align*}X^2 = \pm\frac{2^{{(m-1)}/{2}}(d-2)^2}{\sqrt{d^4 + 24d^2 + 16}}, \quad Y^2 = \pm\frac{2^{{(m-1)}/{2}}(d+2)^2}{\sqrt{d^4 + 24d^2 + 16}},\end{align*} $$
$$ \begin{align*}X^2 = \pm\frac{2^{{(m-1)}/{2}}(d-2)^2}{\sqrt{d^4 + 24d^2 + 16}}, \quad Y^2 = \pm\frac{2^{{(m-1)}/{2}}(d+2)^2}{\sqrt{d^4 + 24d^2 + 16}},\end{align*} $$
where the
![]() $\pm $
signs agree with the
$\pm $
signs agree with the
![]() $\pm $
sign in (3.2). Note that
$\pm $
sign in (3.2). Note that
![]() $X^4,Y^4\in \mathbb {Q}$
. If either of
$X^4,Y^4\in \mathbb {Q}$
. If either of
![]() $X^2$
or
$X^2$
or
![]() $Y^2\in \mathbb {Q}$
, then both are rational and
$Y^2\in \mathbb {Q}$
, then both are rational and
![]() $T\in \mathbb {Q}$
, which contradicts
$T\in \mathbb {Q}$
, which contradicts
![]() $T^2\not \in \mathbb {Q}$
. Thus, we find that
$T^2\not \in \mathbb {Q}$
. Thus, we find that
![]() $X^4,Y^4\in \mathbb {Q}$
, while neither
$X^4,Y^4\in \mathbb {Q}$
, while neither
![]() $X^2\in \mathbb {Q}$
nor
$X^2\in \mathbb {Q}$
nor
![]() $Y^2\in \mathbb {Q}$
. Letting
$Y^2\in \mathbb {Q}$
. Letting
![]() $X=r+s\sqrt {n}$
with
$X=r+s\sqrt {n}$
with
![]() $r,s\in \mathbb {Q}$
, and expanding
$r,s\in \mathbb {Q}$
, and expanding
![]() $X^2$
and
$X^2$
and
![]() $X^4$
, yields
$X^4$
, yields
![]() $rs\neq 0$
and
$rs\neq 0$
and
![]() $rs(r^2+s^2n)=0$
. So
$rs(r^2+s^2n)=0$
. So
![]() $n=-r^2/s^2$
. Since n is a squarefree integer,
$n=-r^2/s^2$
. Since n is a squarefree integer,
![]() $n=-1$
and
$n=-1$
and
![]() $s=r$
. Thus,
$s=r$
. Thus,
![]() $X=r(1+\sqrt {-1})$
and
$X=r(1+\sqrt {-1})$
and
![]() $X^4=-4r^4$
. Similarly,
$X^4=-4r^4$
. Similarly,
![]() $Y^4=-4r_1^4$
for some
$Y^4=-4r_1^4$
for some
![]() $r_1\in \mathbb {Q}$
. However, this means that
$r_1\in \mathbb {Q}$
. However, this means that
![]() $X^4+Y^4 < 0$
, which contradicts
$X^4+Y^4 < 0$
, which contradicts
![]() $X^4+Y^4=2^m$
.
$X^4+Y^4=2^m$
.
For
![]() $c=4$
, we substitute the values for T into (1.2) separately. In the first place, for
$c=4$
, we substitute the values for T into (1.2) separately. In the first place, for
![]() $T=(-d^2-8+\sqrt {d^2+64})/4d$
, we find
$T=(-d^2-8+\sqrt {d^2+64})/4d$
, we find
 $$ \begin{align*}X^2 = 2^{{(m-1)}/{2}}\cdot\frac{-4d - \sqrt{d^4 + 64} }{d^2 + 8}, \quad Y^2 = 2^{{(m-1)}/{2}}\cdot\frac{4d - \sqrt{d^4 + 64} }{d^2 + 8}.\end{align*} $$
$$ \begin{align*}X^2 = 2^{{(m-1)}/{2}}\cdot\frac{-4d - \sqrt{d^4 + 64} }{d^2 + 8}, \quad Y^2 = 2^{{(m-1)}/{2}}\cdot\frac{4d - \sqrt{d^4 + 64} }{d^2 + 8}.\end{align*} $$
Second, for
![]() $T=(-d^2-8-\sqrt {d^2+64})/4d$
, we find
$T=(-d^2-8-\sqrt {d^2+64})/4d$
, we find
 $$ \begin{align*}X^2 = 2^{{(m-1)}/{2}}\cdot\frac{-4d + \sqrt{d^4 + 64} }{d^2 + 8}, \quad Y^2 = 2^{{(m-1)}/{2}}\cdot\frac{4d + \sqrt{d^4 + 64} }{d^2 + 8}.\end{align*} $$
$$ \begin{align*}X^2 = 2^{{(m-1)}/{2}}\cdot\frac{-4d + \sqrt{d^4 + 64} }{d^2 + 8}, \quad Y^2 = 2^{{(m-1)}/{2}}\cdot\frac{4d + \sqrt{d^4 + 64} }{d^2 + 8}.\end{align*} $$
Since Lebesgue [Reference Lebesgue6] proved that the Fermat quartic
![]() $x^4+2^my^4=z^2$
has only nonzero integer solutions for
$x^4+2^my^4=z^2$
has only nonzero integer solutions for
![]() $m \equiv 2 \pmod {4}$
and
$m \equiv 2 \pmod {4}$
and
![]() $d\in \mathbb {Q}$
is nonzero,
$d\in \mathbb {Q}$
is nonzero,
![]() $\sqrt {d^4 + 64}\not \in \mathbb {Q}$
. Thus,
$\sqrt {d^4 + 64}\not \in \mathbb {Q}$
. Thus,
![]() ${K=\mathbb {Q}(\sqrt {d^4+64})}$
is a real-valued quadratic field. Consider the square of any element of K, namely
${K=\mathbb {Q}(\sqrt {d^4+64})}$
is a real-valued quadratic field. Consider the square of any element of K, namely
![]() $(a+b\sqrt {d^4+64})^2=a^2+b^2(d^4+64)+2ab\sqrt {d^4+64}$
. Notice that the rational summand is positive. This leads to a contradiction in the expressions for
$(a+b\sqrt {d^4+64})^2=a^2+b^2(d^4+64)+2ab\sqrt {d^4+64}$
. Notice that the rational summand is positive. This leads to a contradiction in the expressions for
![]() $X^2$
and
$X^2$
and
![]() $Y^2$
, since
$Y^2$
, since
![]() $-4d$
and
$-4d$
and
![]() $4d$
have opposite signs.
$4d$
have opposite signs.
Proposition 3.2. Let
![]() $K=\mathbb {Q}(\sqrt {n})$
with
$K=\mathbb {Q}(\sqrt {n})$
with
![]() $n\in \mathbb {Z}$
squarefree. There are no quadratic solutions
$n\in \mathbb {Z}$
squarefree. There are no quadratic solutions
![]() $(X,Y)\in K\times K$
to the curve
$(X,Y)\in K\times K$
to the curve
![]() $X^4 + Y^4 = 8$
with
$X^4 + Y^4 = 8$
with
![]() $(X, Y)$
a quadratic conjugate pair. However, there are infinitely many quadratic fields K that contain a quadratic conjugate pair solution to the Fermat quartic
$(X, Y)$
a quadratic conjugate pair. However, there are infinitely many quadratic fields K that contain a quadratic conjugate pair solution to the Fermat quartic
![]() $X^4+Y^4=2$
, each derived from one of the infinitely many rational points on the elliptic curve
$X^4+Y^4=2$
, each derived from one of the infinitely many rational points on the elliptic curve
![]() $y^2 = x^3 - 2x$
.
$y^2 = x^3 - 2x$
.
Proof. We begin with
![]() $m = 1$
and suppose there exists a solution
$m = 1$
and suppose there exists a solution
![]() $(X,Y)\in K\times K$
to
$(X,Y)\in K\times K$
to
![]() $X^4+Y^4=2$
with
$X^4+Y^4=2$
with
![]() $X=a+b\sqrt {n}$
,
$X=a+b\sqrt {n}$
,
![]() $Y=\pm (a-b\sqrt {n})$
for some
$Y=\pm (a-b\sqrt {n})$
for some
![]() $a,b\in \mathbb {Q}$
. Expanding
$a,b\in \mathbb {Q}$
. Expanding
![]() $(a+ b\sqrt {n}) ^4 + (a - b\sqrt {n})^4 = 2$
produces
$(a+ b\sqrt {n}) ^4 + (a - b\sqrt {n})^4 = 2$
produces
![]() $a^4 + 6a^2b^2n + b^4n^2 = 1$
. The change of variable
$a^4 + 6a^2b^2n + b^4n^2 = 1$
. The change of variable
![]() $b^2n = c- 3a^2$
yields
$b^2n = c- 3a^2$
yields
![]() $c^2 - 8a^4 = 1$
. Then, the further change of variables
$c^2 - 8a^4 = 1$
. Then, the further change of variables
 $$ \begin{align*}(a, c) = \bigg( \frac{x}{y}, \frac{y^2 - 2x^3}{y^2} \bigg) \implies b^2n = \frac{y^2 - 2x^3 - 3x^2}{y^2} = \frac{-x^3 - 3x^2 - 2x}{y^2}\end{align*} $$
$$ \begin{align*}(a, c) = \bigg( \frac{x}{y}, \frac{y^2 - 2x^3}{y^2} \bigg) \implies b^2n = \frac{y^2 - 2x^3 - 3x^2}{y^2} = \frac{-x^3 - 3x^2 - 2x}{y^2}\end{align*} $$
yields a rational point on the the elliptic curve
![]() $y^2 = x^3 - 2x$
with LMFDB label 256.b1, Mordell–Weil group
$y^2 = x^3 - 2x$
with LMFDB label 256.b1, Mordell–Weil group
![]() $\mathbb {Z} \oplus \mathbb {Z}/2\mathbb {Z}$
with point
$\mathbb {Z} \oplus \mathbb {Z}/2\mathbb {Z}$
with point
![]() $(2, 2)$
of infinite order.
$(2, 2)$
of infinite order.
Working backwards from any rational point
![]() $(a,b)\neq (0,0)$
on the elliptic curve
$(a,b)\neq (0,0)$
on the elliptic curve
![]() ${y^2 = x^3 - 2x}$
to
${y^2 = x^3 - 2x}$
to
![]() $X^4 + Y^4 = 2$
yields the solution
$X^4 + Y^4 = 2$
yields the solution
 $$ \begin{align*}\bigg(\frac{a + \sqrt{-a^3 -3a^2 -2a}}{b} \bigg)^4 + \bigg(\frac{a - \sqrt{-a^3 - 3a^2 - 2a}}{b} \bigg)^4 = 2\end{align*} $$
$$ \begin{align*}\bigg(\frac{a + \sqrt{-a^3 -3a^2 -2a}}{b} \bigg)^4 + \bigg(\frac{a - \sqrt{-a^3 - 3a^2 - 2a}}{b} \bigg)^4 = 2\end{align*} $$
in the field
![]() $K=\mathbb {Q} (\sqrt {-a^3 - 3a^2 - 2a})$
. Since, as Lebesgue proved, there are no nontrivial rational points on
$K=\mathbb {Q} (\sqrt {-a^3 - 3a^2 - 2a})$
. Since, as Lebesgue proved, there are no nontrivial rational points on
![]() $X^4 + Y^4 = 2$
, it follows that
$X^4 + Y^4 = 2$
, it follows that
![]() $\sqrt {-a^3 - 3a^2 - 2a}\not \in \mathbb {Q}$
and K is a quadratic extension of
$\sqrt {-a^3 - 3a^2 - 2a}\not \in \mathbb {Q}$
and K is a quadratic extension of
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
We now use Falting’s theorem and the fact that
![]() $X^4+Y^4=2$
is a nonsingular curve of genus 3 to prove there are infinitely many different quadratic fields
$X^4+Y^4=2$
is a nonsingular curve of genus 3 to prove there are infinitely many different quadratic fields
![]() $\mathbb {Q} (\sqrt {-a^3 - 3a^2 - 2a})$
with
$\mathbb {Q} (\sqrt {-a^3 - 3a^2 - 2a})$
with
![]() $(a, b)$
a rational point on the elliptic curve
$(a, b)$
a rational point on the elliptic curve
![]() $y^2 = x^3 - 2x$
. Since each quadratic field K contains only finitely many solutions to
$y^2 = x^3 - 2x$
. Since each quadratic field K contains only finitely many solutions to
![]() $X^4+Y^4=2$
, this result will follow once we establish the fact that there are infinitely many different values of
$X^4+Y^4=2$
, this result will follow once we establish the fact that there are infinitely many different values of
 $$ \begin{align*}A(x,y)=\frac{\sqrt{-x^3 - 3x^2 - 2x}}{y}\in\mathbb{C}.\end{align*} $$
$$ \begin{align*}A(x,y)=\frac{\sqrt{-x^3 - 3x^2 - 2x}}{y}\in\mathbb{C}.\end{align*} $$
Our concern is that there might be simultaneous values
![]() $k=A(x,y)$
that occur for infinitely many different points
$k=A(x,y)$
that occur for infinitely many different points
![]() $(a,b)$
on
$(a,b)$
on
![]() $y^2 = x^3 - 2x$
. So we ask whether there can be any complex values
$y^2 = x^3 - 2x$
. So we ask whether there can be any complex values
![]() $k\in \mathbb {C}$
such that the level curve
$k\in \mathbb {C}$
such that the level curve
![]() $y^2k^2=-x^3 - 3x^2 - 2x$
intersects
$y^2k^2=-x^3 - 3x^2 - 2x$
intersects
![]() $y^2=x^3-2x$
at infinitely many real points
$y^2=x^3-2x$
at infinitely many real points
![]() $(x_1,y_1)$
. Since each intersection point yields a real solution to the polynomial
$(x_1,y_1)$
. Since each intersection point yields a real solution to the polynomial
![]() $k^2(x^3-2x)=-x^3 - 3x^2 - 2x$
, which is a polynomial with no more than three distinct roots, this does not occur.
$k^2(x^3-2x)=-x^3 - 3x^2 - 2x$
, which is a polynomial with no more than three distinct roots, this does not occur.
Now, we let
![]() $m = 3$
and suppose there exists a solution
$m = 3$
and suppose there exists a solution
![]() $(X,Y)\in K\times K$
to the curve
$(X,Y)\in K\times K$
to the curve
![]() $X^4+Y^4=8$
with
$X^4+Y^4=8$
with
![]() $X=a+b\sqrt {n}$
,
$X=a+b\sqrt {n}$
,
![]() $Y=\pm (a-b\sqrt {n})$
for some
$Y=\pm (a-b\sqrt {n})$
for some
![]() $a,b\in \mathbb {Q}$
. Expanding
$a,b\in \mathbb {Q}$
. Expanding
![]() $(a+ b\sqrt {n}) ^4 + (a - b\sqrt {n})^4 = 8$
produces
$(a+ b\sqrt {n}) ^4 + (a - b\sqrt {n})^4 = 8$
produces
![]() $a^4 + 6a^2b^2n + b^4n^2 = 4$
. The change of variable
$a^4 + 6a^2b^2n + b^4n^2 = 4$
. The change of variable
![]() $b^2n = c- 3a^2$
now yields
$b^2n = c- 3a^2$
now yields
![]() $c^2 - 8a^4 = 4$
. Using the rational point
$c^2 - 8a^4 = 4$
. Using the rational point
![]() $(a, c) = (0,2)$
and [Reference Mordell9, Theorem 2 on page 77] yields a birational equivalence with the elliptic curve
$(a, c) = (0,2)$
and [Reference Mordell9, Theorem 2 on page 77] yields a birational equivalence with the elliptic curve
![]() $y^2 = x^3 - 8x$
LMFDB label 256.c1, which has Mordell–Weil group
$y^2 = x^3 - 8x$
LMFDB label 256.c1, which has Mordell–Weil group
![]() $\mathbb {Z} / 2\mathbb {Z}$
and only the trivial rational point
$\mathbb {Z} / 2\mathbb {Z}$
and only the trivial rational point
![]() $(0, 0)$
. Working backwards from this point and the point at infinity, we obtain two points
$(0, 0)$
. Working backwards from this point and the point at infinity, we obtain two points
![]() $(x:y:z) = (0:2:1)$
and
$(x:y:z) = (0:2:1)$
and
![]() $(0:1:0)$
on the projective version of our curve
$(0:1:0)$
on the projective version of our curve
![]() $y^2z^2-8x^4=4z^4$
. The only rational point on
$y^2z^2-8x^4=4z^4$
. The only rational point on
![]() $c^2 - 8a^4 = 4$
is
$c^2 - 8a^4 = 4$
is
![]() $(a, c) = (0,2)$
. Since
$(a, c) = (0,2)$
. Since
![]() $a=0$
, this contradicts our assumption that a and b are both nonzero.
$a=0$
, this contradicts our assumption that a and b are both nonzero.
Example 3.3. Using the generator
![]() $(a, b) = (2, 2)$
of the elliptic curve
$(a, b) = (2, 2)$
of the elliptic curve
![]() $y^2 = x^3 - 2x$
gives a solution in the quadratic field
$y^2 = x^3 - 2x$
gives a solution in the quadratic field
![]() $\mathbb {Q}(\sqrt {-6})$
to the curve
$\mathbb {Q}(\sqrt {-6})$
to the curve
![]() $X^4 + Y^4 = 2$
, namely
$X^4 + Y^4 = 2$
, namely
Example 3.4. If we add the torsion point
![]() $(0, 0)$
and the nontorsion generator
$(0, 0)$
and the nontorsion generator
![]() $(2, 2)$
under the group law of the elliptic curve
$(2, 2)$
under the group law of the elliptic curve
![]() $y^2 = x^3 - 2x$
, we get the point
$y^2 = x^3 - 2x$
, we get the point
![]() $(-1, -1)$
. Doubling this point gives us the point
$(-1, -1)$
. Doubling this point gives us the point
![]() $(a, b) = (9/4, 21/8)$
. Using the point
$(a, b) = (9/4, 21/8)$
. Using the point
![]() $(a, b)$
to find a solution to
$(a, b)$
to find a solution to
![]() $X^4 + Y^4 = 2$
gives the quadratic field
$X^4 + Y^4 = 2$
gives the quadratic field
![]() $\mathbb {Q}(\sqrt {-221})$
with solution
$\mathbb {Q}(\sqrt {-221})$
with solution
 $$ \begin{align*}\bigg( \frac{6 + \sqrt{-221}}{7} \bigg)^4 + \bigg( \frac{6 - \sqrt{-221}}{7} \bigg) ^ 4 = 2 .\end{align*} $$
$$ \begin{align*}\bigg( \frac{6 + \sqrt{-221}}{7} \bigg)^4 + \bigg( \frac{6 - \sqrt{-221}}{7} \bigg) ^ 4 = 2 .\end{align*} $$
Acknowledgement
I sincerely thank my advisor, Dr. Griff Elder, for his guidance, support and the invaluable research opportunity.