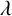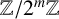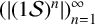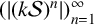Refine search
Actions for selected content:
82 results
Explicit formulas for the Grothendieck class of
 $\overline {\mathcal{M}}_{0,n}$
$\overline {\mathcal{M}}_{0,n}$
- Part of
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Alternating sign matrices with reflective symmetry and plane partitions:
 $n+3$ pairs of equivalent statistics and a Cauchy-type identity
$n+3$ pairs of equivalent statistics and a Cauchy-type identity
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 08 October 2025, e168
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The algebraic structure of Dyson–Schwinger equations with multiple insertion places
- Part of
-
- Journal:
- Canadian Mathematical Communications / Volume 1 / 2025
- Published online by Cambridge University Press:
- 29 August 2025, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ENUMERATION AND DIVISIBILITY OF HIGHER DIMENSIONAL KING WALKS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 28 July 2025, pp. 1-12
-
- Article
- Export citation
Hook length inequalities for t-regular partitions in the t-aspect
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 24 July 2025, pp. 1-12
-
- Article
- Export citation
Integration on complex Grassmannians, deformed monotone Hurwitz numbers, and interlacing phenomena
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 30 June 2025, pp. 1-40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Congruences modulo powers of 5 for partition k-tuples with 5-cores
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 4 / November 2025
- Published online by Cambridge University Press:
- 17 June 2025, pp. 1245-1261
-
- Article
- Export citation
ON
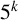 $5^k$-REGULAR PARTITIONS MODULO POWERS OF
$5^k$-REGULAR PARTITIONS MODULO POWERS OF 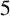 $5$
$5$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 14 April 2025, pp. 449-457
- Print publication:
- December 2025
-
- Article
- Export citation
ON NEW MINIMAL EXCLUDANTS OF OVERPARTITIONS RELATED TO SOME q-SERIES OF RAMANUJAN
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 11 February 2025, pp. 1-13
- Print publication:
- August 2025
-
- Article
- Export citation
Pebble trees
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 10 February 2025, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bounded Littlewood identity related to alternating sign matrices
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 13 December 2024, e124
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FROBENIUS NUMBERS ASSOCIATED WITH DIOPHANTINE TRIPLES OF
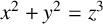 $x^2+y^2=z^3$
$x^2+y^2=z^3$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 14 November 2024, pp. 57-66
- Print publication:
- August 2025
-
- Article
- Export citation
Two-sided permutation statistics via symmetric functions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 07 November 2024, e93
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOME COUNTING FORMULAE FOR
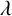 $\lambda $-QUIDDITIES OVER THE RINGS
$\lambda $-QUIDDITIES OVER THE RINGS 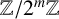 ${\mathbb {Z}}/2^{m}{\mathbb {Z}}$
${\mathbb {Z}}/2^{m}{\mathbb {Z}}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 16 May 2024, pp. 1-12
- Print publication:
- February 2025
-
- Article
- Export citation
Some congruences for 12-coloured generalized Frobenius partitions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 02 May 2024, pp. 778-793
-
- Article
- Export citation
The distribution of the maximum protection number in simply generated trees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 12 April 2024, pp. 518-553
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Lattice points in slices of prisms
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 08 March 2024, pp. 1013-1040
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GENERATING FUNCTIONS FOR THE QUOTIENTS OF NUMERICAL SEMIGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 29 February 2024, pp. 427-438
- Print publication:
- December 2024
-
- Article
- Export citation
COUNTING UNIONS OF SCHREIER SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 27 December 2023, pp. 19-31
- Print publication:
- August 2024
-
- Article
- Export citation
Partitions with parts separated by parity: conjugation, congruences and the mock theta functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 30 November 2023, pp. 954-974
- Print publication:
- June 2025
-
- Article
- Export citation




















































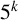
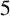



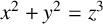







 . We give a general approach, based on the theory of symmetric functions, for finding the joint distribution of
. We give a general approach, based on the theory of symmetric functions, for finding the joint distribution of