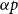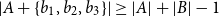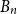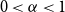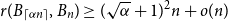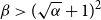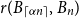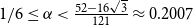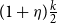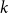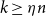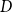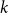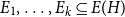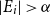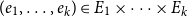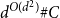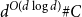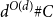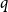Contents
Paper
Small subsets with large sumset: Beyond the Cauchy–Davenport bound
- Part of:
-
- Published online by Cambridge University Press:
- 21 February 2024, pp. 411-431
-
- Article
- Export citation
On a conjecture of Conlon, Fox, and Wigderson
- Part of:
-
- Published online by Cambridge University Press:
- 16 February 2024, pp. 432-445
-
- Article
- Export citation
Antidirected subgraphs of oriented graphs
- Part of:
-
- Published online by Cambridge University Press:
- 06 March 2024, pp. 446-466
-
- Article
- Export citation
Large monochromatic components in expansive hypergraphs
- Part of:
-
- Published online by Cambridge University Press:
- 05 March 2024, pp. 467-483
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sharp bounds for a discrete John’s theorem
- Part of:
-
- Published online by Cambridge University Press:
- 05 March 2024, pp. 484-486
-
- Article
- Export citation
Algorithms for the ferromagnetic Potts model on expanders
- Part of:
-
- Published online by Cambridge University Press:
- 05 April 2024, pp. 487-517
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The distribution of the maximum protection number in simply generated trees
- Part of:
-
- Published online by Cambridge University Press:
- 12 April 2024, pp. 518-553
-
- Article
-
- You have access
- Open access
- HTML
- Export citation