No CrossRef data available.
Article contents
Sharp bounds for a discrete John’s theorem
Published online by Cambridge University Press: 05 March 2024
Abstract
Tao and Vu showed that every centrally symmetric convex progression 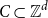 $C\subset \mathbb{Z}^d$ is contained in a generalized arithmetic progression of size
$C\subset \mathbb{Z}^d$ is contained in a generalized arithmetic progression of size 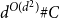 $d^{O(d^2)} \# C$. Berg and Henk improved the size bound to
$d^{O(d^2)} \# C$. Berg and Henk improved the size bound to 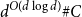 $d^{O(d\log d)} \# C$. We obtain the bound
$d^{O(d\log d)} \# C$. We obtain the bound 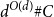 $d^{O(d)} \# C$, which is sharp up to the implied constant and is of the same form as the bound in the continuous setting given by John’s theorem.
$d^{O(d)} \# C$, which is sharp up to the implied constant and is of the same form as the bound in the continuous setting given by John’s theorem.
MSC classification
Secondary:
52A27: Approximation by convex sets
Information
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
Berg, S. L. and Henk, M. (2019) Discrete analogues of John’s theorem. Moscow J. Comb. Number Theory 8(4) 367–378.CrossRefGoogle Scholar
John, F. (1948) Extremum problems with inequalities as subsidiary conditions. In Studies and Essays, Presented to R. Courant on his 60th Birthday,. New York: Interscience, pp. 187–204.Google Scholar
Lovett, S. and Regev, O. (2017) A counterexample to a strong variant of the Polynomial Freiman-Ruzsa Conjecture in Euclidean space. Discrete Anal. 8 379–388.Google Scholar
Tao, T. and Vu, V. (2006) Additive Combinatorics. Cambridge University Press, Vol. 105.CrossRefGoogle Scholar
Tao, T. and Van, V. (2008) John-type theorems for generalized arithmetic progressions and iterated sumsets. Adv. Math. 219(2) 428–449.CrossRefGoogle Scholar


