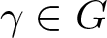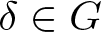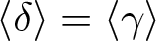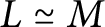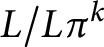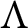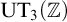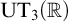Refine search
Actions for selected content:
50 results
RETRACTION OF [J. NEŠETŘIL AND P. OSSONA DE MENDEZ. EXISTENCE OF MODELING LIMITS FOR SEQUENCES OF SPARSE STRUCTURES. THE JOURNAL OF SYMBOLIC LOGIC. 2019;84(2):452–472]
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 11 September 2025, pp. 1-2
-
- Article
- Export citation
CORONA RIGIDITY
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 31 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 30 June 2025, pp. 195-287
- Print publication:
- June 2025
-
- Article
- Export citation
Motivic Vitushkin invariants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 20 August 2025, pp. 959-992
- Print publication:
- May 2025
-
- Article
- Export citation
MULTIPLICATIVE (IN)STABILITY OF BANACH ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 17 March 2025, pp. 194-200
- Print publication:
- August 2025
-
- Article
- Export citation
Structural convergence and algebraic roots
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 392-400
-
- Article
- Export citation
ON THE EXPRESSIVE POWER OF INQUISITIVE EPISTEMIC LOGIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 16 December 2024, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON ULTRAPRODUCTS, THE SPECTRAL THEOREM AND RIGGED HILBERT SPACES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 17 December 2024, pp. 1397-1429
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
New Results in Model Theory and Set Theory
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 30 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 18 March 2025, pp. 543-544
- Print publication:
- December 2024
-
- Article
-
- You have access
- HTML
- Export citation
A NOTE ON THE STRONG ERDŐS–HAJNAL PROPERTY FOR GRAPHS WITH BOUNDED VC-MINIMAL COMPLEXITY
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 15 November 2024, pp. 1-7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Powers of commutators in linear algebraic groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 14 May 2024, pp. 830-837
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MORE ON GALOIS COHOMOLOGY, DEFINABILITY, AND DIFFERENTIAL ALGEBRAIC GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 11 April 2024, pp. 496-515
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTENSIONS AND LIMITS OF THE SPECKER–BLATTER THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 21 March 2024, pp. 1284-1312
- Print publication:
- September 2024
-
- Article
- Export citation
A NEW PERSPECTIVE ON SEMI-RETRACTIONS AND THE RAMSEY PROPERTY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 08 March 2024, pp. 945-979
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON MODEL-THEORETIC CONNECTED GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 89 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 14 November 2023, pp. 50-79
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hensel minimality II: Mixed characteristic and a diophantine application
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 October 2023, e89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cohomology of algebraic varieties over non-archimedean fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 21 October 2022, e94
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hensel minimality I
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 10 / 2022
- Published online by Cambridge University Press:
- 16 May 2022, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Maranda’s theorem for pure-injective modules and duality
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 17 March 2022, pp. 581-607
- Print publication:
- April 2023
-
- Article
- Export citation
BOHR COMPACTIFICATIONS OF GROUPS AND RINGS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 04 February 2022, pp. 1103-1137
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COUNTING SIBLINGS IN UNIVERSAL THEORIES
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 10 January 2022, pp. 1130-1155
- Print publication:
- September 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation