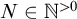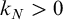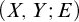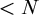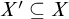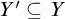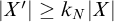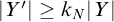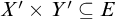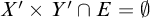1. Introduction
Erdős–Hajnal conjecture [Reference Erdös and Hajnal8] says for any graph H there is
![]() $\epsilon>0$
such that if a graph G does not contain any induced subgraph isomorphic to H then G has a clique or an anti-clique of size
$\epsilon>0$
such that if a graph G does not contain any induced subgraph isomorphic to H then G has a clique or an anti-clique of size
![]() $\geq |G|^\epsilon $
. More generally, we say a family of finite graphs has the Erdős–Hajnal property if there is
$\geq |G|^\epsilon $
. More generally, we say a family of finite graphs has the Erdős–Hajnal property if there is
![]() $\epsilon>0$
such that for any graph G in the family, G has a clique or an anti-clique of size
$\epsilon>0$
such that for any graph G in the family, G has a clique or an anti-clique of size
![]() $\geq |G|^\epsilon $
. A family of finite graphs has the strong Erdős–Hajnal property if there is
$\geq |G|^\epsilon $
. A family of finite graphs has the strong Erdős–Hajnal property if there is
![]() $\epsilon>0$
such that for any graph
$\epsilon>0$
such that for any graph
![]() $G=(V,E)$
in the family, there exist
$G=(V,E)$
in the family, there exist
![]() $X,Y\subseteq V$
such that
$X,Y\subseteq V$
such that
![]() $X\cap Y=\emptyset $
,
$X\cap Y=\emptyset $
,
![]() $|X|\geq \epsilon |V|$
,
$|X|\geq \epsilon |V|$
,
![]() $|Y|\geq \epsilon |V|$
, and
$|Y|\geq \epsilon |V|$
, and
![]() $X\times Y\subseteq E$
or
$X\times Y\subseteq E$
or
![]() $X\times Y\subseteq \neg E$
. The strong Erdős–Hajnal property implies the Erdős-Hajnal property (see [Reference Alon, Pach, Pinchasi, Radoičić and Sharir2, Theorem 1.2.]). Malliaris and Shelah proved in [Reference Malliaris and Shelah12] that the family of stable graphs has the Erdős–Hajnal property. Chernikov and Starchenko gave another proof for stable graphs in [Reference Chernikov and Starchenko3] and in [Reference Chernikov and Starchenko4] they proved that the family of distal graphs has the strong Erdős–Hajnal property. In general, we are interested in whether the family of bounded VC-dimension (i.e., NIP [Reference Simon14]) graphs, which contains both stable graphs and distal graphs, has the Erdős–Hajnal property. Motivation for studying this problem was given in [Reference Fox, Pach and Suk10], which also gave a lower bound
$X\times Y\subseteq \neg E$
. The strong Erdős–Hajnal property implies the Erdős-Hajnal property (see [Reference Alon, Pach, Pinchasi, Radoičić and Sharir2, Theorem 1.2.]). Malliaris and Shelah proved in [Reference Malliaris and Shelah12] that the family of stable graphs has the Erdős–Hajnal property. Chernikov and Starchenko gave another proof for stable graphs in [Reference Chernikov and Starchenko3] and in [Reference Chernikov and Starchenko4] they proved that the family of distal graphs has the strong Erdős–Hajnal property. In general, we are interested in whether the family of bounded VC-dimension (i.e., NIP [Reference Simon14]) graphs, which contains both stable graphs and distal graphs, has the Erdős–Hajnal property. Motivation for studying this problem was given in [Reference Fox, Pach and Suk10], which also gave a lower bound
![]() $e^{(\log n)^{1-o(1)}}$
for largest clique or anti-clique in a graph with bounded VC-dimension. In this paper, we consider graphs of bounded VC-minimal complexity, a special case of NIP graphs. Roughly speaking, we say a bipartite graph
$e^{(\log n)^{1-o(1)}}$
for largest clique or anti-clique in a graph with bounded VC-dimension. In this paper, we consider graphs of bounded VC-minimal complexity, a special case of NIP graphs. Roughly speaking, we say a bipartite graph
![]() $(X,Y;E)$
has VC-minimal complexity
$(X,Y;E)$
has VC-minimal complexity
![]() $<N$
if for all
$<N$
if for all
![]() $a\in X$
, the set
$a\in X$
, the set
![]() $\{y\in Y: (a,y)\in E\}$
is a finite union of Swiss Cheeses such that the sum of the number of holes and the number of Swiss Cheeses is
$\{y\in Y: (a,y)\in E\}$
is a finite union of Swiss Cheeses such that the sum of the number of holes and the number of Swiss Cheeses is
![]() $<N$
. We will show that the strong Erdős–Hajnal property holds for the family of finite bipartite graphs
$<N$
. We will show that the strong Erdős–Hajnal property holds for the family of finite bipartite graphs
![]() $(X,Y;E)$
of bounded VC-minimal complexity. One example is definable relations
$(X,Y;E)$
of bounded VC-minimal complexity. One example is definable relations
![]() $E(x,y)$
with
$E(x,y)$
with
![]() $|x|=1,|y|=1$
in
$|x|=1,|y|=1$
in
![]() $ACVF$
(algebraically closed valued field). Since
$ACVF$
(algebraically closed valued field). Since
![]() $ACVF$
allows Swiss Cheese decomposition [Reference Holly11], given any
$ACVF$
allows Swiss Cheese decomposition [Reference Holly11], given any
![]() $\mathcal {M}\models ACVF$
and any definable relation
$\mathcal {M}\models ACVF$
and any definable relation
![]() $E \subseteq M\times M$
, the family
$E \subseteq M\times M$
, the family
![]() $\{(X,Y;E_{\upharpoonright X\times Y}):X,Y$
finite subsets of
$\{(X,Y;E_{\upharpoonright X\times Y}):X,Y$
finite subsets of
![]() $M\}$
has bounded VC-minimal complexity, and thus the strong Erdős–Hajnal property holds. This partially generalizes [Reference Chernikov and Starchenko4, Example 4.11(2)].
$M\}$
has bounded VC-minimal complexity, and thus the strong Erdős–Hajnal property holds. This partially generalizes [Reference Chernikov and Starchenko4, Example 4.11(2)].
Recently, in [Reference Nguyen, Scott and Seymour13], Nguyen, Scott, and Seymour proved that any family of finite graphs with bounded VC-dimension has the Erdős–Hajnal property, which gave another proof that any family of finite graphs with bounded VC-minimal complexity has the Erdős–Hajnal property.
In addition to its relation with the Erdős–Hajnal property, the strong Erdős–Hajnal property is of independent interest. On one hand, in model theory, partitioned formulas and hence bipartite graphs are often used (e.g., definition of stable formulas and definition of NIP formulas). On the other hand, in [Reference Erdos, Hajnal and Pach9, Theorem 1], Erdős, Hajnal, and Pach proved the following fact:
Fact 1.1. Let H be a fixed graph with k vertices. Any H-free graph with n vertices or its complement has a complete bi-partite subgraph with
![]() $\lfloor (n/k)^{1/(k-1)}\rfloor $
vertices in its classes.
$\lfloor (n/k)^{1/(k-1)}\rfloor $
vertices in its classes.
This fact roughly says that given a fixed H, for any H-free graph, there exists in it or in its complement a complete bipartite graph of polynomial size. So it’s natural to ask when we can find in a graph or its complement a complete bipartite graph of linear size. A random graph argument in [Reference Choromanski, Falik, Liebenau, Patel and Pilipczuk5] together with results in [Reference Chudnovsky, Scott, Seymour and Spirkl6] characterized families of graphs that are defined by omitting a finite set of graphs and satisfy the strong Erdős–Hajnal property: If a family of graphs is defined by omitting a finite set of graphs, then it has the strong Erdős–Hajnal property iff it omits some forest together with its complement. We will show that the family of all forests has bounded VC-minimal complexity and thus, the case of bounded VC-minimal complexity is not covered in [Reference Chudnovsky, Scott, Seymour and Spirkl6]. It is also an example where a family of graphs has bounded VC-minimal complexity and is not defined by omitting a finite set of graphs.
We will prove the following main theorem:
Theorem 1.2. For
![]() $N>0$
, let
$N>0$
, let
![]() $k_N=\dfrac {1}{2^{N+4}}$
. If a finite bipartite graph
$k_N=\dfrac {1}{2^{N+4}}$
. If a finite bipartite graph
![]() $(X,Y;E)$
has VC-minimal complexity
$(X,Y;E)$
has VC-minimal complexity
![]() $<N$
then there exist
$<N$
then there exist
![]() $X'\subseteq X$
,
$X'\subseteq X$
,
![]() $Y'\subseteq Y$
with
$Y'\subseteq Y$
with
![]() $|X'|\geq k_N|X|$
,
$|X'|\geq k_N|X|$
,
![]() $|Y'|\geq k_N|Y|$
such that
$|Y'|\geq k_N|Y|$
such that
![]() $X'\times Y'\subseteq E$
or
$X'\times Y'\subseteq E$
or
![]() $X'\times Y'\cap E=\emptyset $
.
$X'\times Y'\cap E=\emptyset $
.
2. Preliminaries
The following Definitions 2.1, 2.2, 2.5 are based on notions in [Reference Adler1].
Definition 2.1. Given a set U, a family of subsets
![]() $\Psi =\{B_i:i\in I\}\subseteq \mathcal {P}(U)$
, where I is some index set, is called a directed family if for any
$\Psi =\{B_i:i\in I\}\subseteq \mathcal {P}(U)$
, where I is some index set, is called a directed family if for any
![]() $B_i,B_j\in \Psi $
,
$B_i,B_j\in \Psi $
,
![]() $B_i\subseteq B_j$
or
$B_i\subseteq B_j$
or
![]() $B_j \subseteq B_i$
or
$B_j \subseteq B_i$
or
![]() $B_i\cap B_j=\emptyset $
.
$B_i\cap B_j=\emptyset $
.
Definition 2.2. Given a directed family
![]() $\Psi $
of subsets of U, a set
$\Psi $
of subsets of U, a set
![]() $B\in \Psi $
is a called a
$B\in \Psi $
is a called a
![]() $\Psi $
-ball. A set
$\Psi $
-ball. A set
![]() $S \subseteq U$
is a
$S \subseteq U$
is a
![]() $\Psi $
-Swiss cheese if
$\Psi $
-Swiss cheese if
![]() $S = B \setminus (B_0 \cup \dots \cup B_n)$
, where each of
$S = B \setminus (B_0 \cup \dots \cup B_n)$
, where each of
![]() $B,B_0,\dots ,B_n$
is a
$B,B_0,\dots ,B_n$
is a
![]() $\Psi $
-ball. We will call B an outer ball of S, and each
$\Psi $
-ball. We will call B an outer ball of S, and each
![]() $B_i$
is called a hole of S.
$B_i$
is called a hole of S.
Definition 2.3. A graph G is a pair
![]() $(V,E)$
where V is a finite set of vertices and
$(V,E)$
where V is a finite set of vertices and
![]() $E\subseteq V\times V$
is a binary symmetric anti-reflexive relation.
$E\subseteq V\times V$
is a binary symmetric anti-reflexive relation.
Definition 2.4. A bipartite graph is a triple
![]() $(X,Y;E)$
where X, Y are finite sets and
$(X,Y;E)$
where X, Y are finite sets and
![]() $E\subseteq X\times Y$
.
$E\subseteq X\times Y$
.
Notation. Given a bipartite graph
![]() $(X,Y;E)$
,
$(X,Y;E)$
,
![]() $a\in X$
,
$a\in X$
,
![]() $S\subseteq Y$
, we define
$S\subseteq Y$
, we define
![]() $E(a,S)$
as the set
$E(a,S)$
as the set
![]() $\{b\in S: (a,b)\in E\}$
.
$\{b\in S: (a,b)\in E\}$
.
Definition 2.5. Given a finite bipartite graph
![]() $(X,Y;E)$
, we say it has VC-minimal complexity
$(X,Y;E)$
, we say it has VC-minimal complexity
![]() $<N$
if there is a directed family
$<N$
if there is a directed family
![]() $\Psi $
of subsets of Y such that for each
$\Psi $
of subsets of Y such that for each
![]() $a\in X$
,
$a\in X$
,
![]() $E(a,Y)$
is a finite disjoint union of
$E(a,Y)$
is a finite disjoint union of
![]() $\Psi $
-Swiss cheeses and the number of outer balls
$\Psi $
-Swiss cheeses and the number of outer balls
![]() $+$
the number of holes
$+$
the number of holes
![]() $<N$
. That is,
$<N$
. That is,
![]() $E(a,Y)=(B_{11}\setminus (B_{12}\cup \dots \cup B_{1d(1)}))$
$E(a,Y)=(B_{11}\setminus (B_{12}\cup \dots \cup B_{1d(1)}))$
![]() $\dot \cup $
$\dot \cup $
![]() $\cdots $
$\cdots $
![]() $\dot \cup $
$\dot \cup $
![]() $(B_{s1}\setminus (B_{s2}\cup \dots \cup B_{sd(s)}))$
where
$(B_{s1}\setminus (B_{s2}\cup \dots \cup B_{sd(s)}))$
where
![]() $d(1)+\dots +d(s)<N$
.
$d(1)+\dots +d(s)<N$
.
3. Proof
Theorem 3.1. For
![]() $N>0$
, let
$N>0$
, let
![]() $k_N=\dfrac {1}{2^{N+4}}$
. If a finite bipartite graph
$k_N=\dfrac {1}{2^{N+4}}$
. If a finite bipartite graph
![]() $(X,Y;E)$
has VC-minimal complexity
$(X,Y;E)$
has VC-minimal complexity
![]() $<N$
then there exist
$<N$
then there exist
![]() $X'\subseteq X$
,
$X'\subseteq X$
,
![]() $Y'\subseteq Y$
with
$Y'\subseteq Y$
with
![]() $|X'|\geq k_N|X|$
,
$|X'|\geq k_N|X|$
,
![]() $|Y'|\geq k_N|Y|$
such that
$|Y'|\geq k_N|Y|$
such that
![]() $X'\times Y'\subseteq E$
or
$X'\times Y'\subseteq E$
or
![]() $X'\times Y' \cap E=\emptyset $
.
$X'\times Y' \cap E=\emptyset $
.
Proof. We prove by induction on N. If
![]() $N=1$
then for all
$N=1$
then for all
![]() $a\in X$
,
$a\in X$
,
![]() $E(a,Y)=\emptyset $
. So
$E(a,Y)=\emptyset $
. So
![]() $X\times Y\subseteq \neg E$
.
$X\times Y\subseteq \neg E$
.
Suppose true for N and we show for
![]() $N+1$
.
$N+1$
.
Let
![]() $(X,Y;E)$
be a finite bipartite graph with VC-minimal complexity
$(X,Y;E)$
be a finite bipartite graph with VC-minimal complexity
![]() $<N+1$
. Then there is a directed family
$<N+1$
. Then there is a directed family
![]() $\Psi $
such that for each
$\Psi $
such that for each
![]() $a\in X$
,
$a\in X$
,
where the
![]() $B^a_{kl}$
’s are
$B^a_{kl}$
’s are
![]() $\Psi $
-balls and
$\Psi $
-balls and
![]() $d(1)+\dots +d(s_a)<N+1$
. Consider the finite family
$d(1)+\dots +d(s_a)<N+1$
. Consider the finite family
Since
![]() $\mathcal {F}$
is finite and
$\mathcal {F}$
is finite and
![]() $|Y|\geq \frac {1}{8}|Y|$
, there is a minimal
$|Y|\geq \frac {1}{8}|Y|$
, there is a minimal
![]() $Z\in \mathcal {F}$
such that
$Z\in \mathcal {F}$
such that
![]() $|Z|\geq \frac {1}{8}|Y|$
(minimal with respect to the partial order
$|Z|\geq \frac {1}{8}|Y|$
(minimal with respect to the partial order
![]() $\subseteq $
). Let
$\subseteq $
). Let
Let
![]() $C_1,\dots ,C_m$
be maximal elements in
$C_1,\dots ,C_m$
be maximal elements in
![]() $\mathcal {F}'$
. Then
$\mathcal {F}'$
. Then
![]() $\forall a\in X$
,
$\forall a\in X$
,
![]() $\forall k,l \in \mathbb {N}$
,
$\forall k,l \in \mathbb {N}$
,
![]() $\forall t\in \{1,\dots ,m\}$
, if
$\forall t\in \{1,\dots ,m\}$
, if
![]() $B^a_{kl}\subsetneq Z$
then
$B^a_{kl}\subsetneq Z$
then
![]() $B^a_{kl}\cap C_t=\emptyset $
or
$B^a_{kl}\cap C_t=\emptyset $
or
![]() $B^a_{kl}\subseteq C_{t}$
. Let
$B^a_{kl}\subseteq C_{t}$
. Let
![]() $R=Z\setminus (C_1\cup \dots \cup C_{m})$
.
$R=Z\setminus (C_1\cup \dots \cup C_{m})$
.
Claim 3.2.
![]() $\forall a\in X$
,
$\forall a\in X$
,
![]() $E(a,R)=R$
or
$E(a,R)=R$
or
![]() $E(a,R)=\emptyset $
.
$E(a,R)=\emptyset $
.
Proof.
![]() $E(a,Y){\kern-1.2pt}={\kern-1.2pt}(B^a_{11}{\kern-1.5pt}\setminus{\kern-1.5pt} (B^a_{12}{\kern-1.2pt}\cup \dots \cup{\kern-1.2pt} B^a_{1d(1)}))$
$E(a,Y){\kern-1.2pt}={\kern-1.2pt}(B^a_{11}{\kern-1.5pt}\setminus{\kern-1.5pt} (B^a_{12}{\kern-1.2pt}\cup \dots \cup{\kern-1.2pt} B^a_{1d(1)}))$
![]() $\dot \cup $
$\dot \cup $
![]() $\dots $
$\dots $
![]() $\dot \cup $
$\dot \cup $
![]() $(B^a_{s_a1}{\kern-1.2pt}\setminus{\kern-1.2pt} (B^a_{s_a2}{\kern-1.2pt}\cup \dots \cup{\kern-1.2pt} B^a_{s_ad(s_a)}))$
. Suppose
$(B^a_{s_a1}{\kern-1.2pt}\setminus{\kern-1.2pt} (B^a_{s_a2}{\kern-1.2pt}\cup \dots \cup{\kern-1.2pt} B^a_{s_ad(s_a)}))$
. Suppose
![]() $E(a,R)\neq \emptyset $
. Then for some
$E(a,R)\neq \emptyset $
. Then for some
![]() $k\in \{1,\dots ,s_a\}$
,
$k\in \{1,\dots ,s_a\}$
,
May assume
![]() $(B^a_{11}\setminus (B^a_{12}\cup \dots \cup B^a_{1d(1)}))\cap R\neq \emptyset $
. So
$(B^a_{11}\setminus (B^a_{12}\cup \dots \cup B^a_{1d(1)}))\cap R\neq \emptyset $
. So
![]() $B^a_{11}\cap Z\neq \emptyset $
. Since Z is Y or a
$B^a_{11}\cap Z\neq \emptyset $
. Since Z is Y or a
![]() $\Psi $
-ball,
$\Psi $
-ball,
![]() $B^a_{11}\subsetneq Z$
or
$B^a_{11}\subsetneq Z$
or
![]() $B^a_{11}\supseteq Z$
. If
$B^a_{11}\supseteq Z$
. If
![]() $B^a_{11}\subsetneq Z$
then
$B^a_{11}\subsetneq Z$
then
![]() $B^a_{11}\subseteq C_1\cup \dots \cup C_{m}$
and
$B^a_{11}\subseteq C_1\cup \dots \cup C_{m}$
and
![]() $B^a_{11}\cap R=\emptyset $
, a contradiction. Hence
$B^a_{11}\cap R=\emptyset $
, a contradiction. Hence
![]() $B^a_{11}\supseteq Z$
. Similarly, for any hole
$B^a_{11}\supseteq Z$
. Similarly, for any hole
![]() $K\in \{B^a_{12},\dots ,B^a_{1d(1)}\}$
, if
$K\in \{B^a_{12},\dots ,B^a_{1d(1)}\}$
, if
![]() $K\cap R\neq \emptyset $
, then
$K\cap R\neq \emptyset $
, then
![]() $K\subsetneq Z$
or
$K\subsetneq Z$
or
![]() $K\supseteq Z$
. If
$K\supseteq Z$
. If
![]() $K\subsetneq Z$
then
$K\subsetneq Z$
then
![]() $K\subseteq C_1\cup \dots \cup C_{m}$
and
$K\subseteq C_1\cup \dots \cup C_{m}$
and
![]() $K\cap R=\emptyset $
, a contradiction. If
$K\cap R=\emptyset $
, a contradiction. If
![]() $K\supseteq Z$
, then
$K\supseteq Z$
, then
a contradiction. Hence we must have
![]() $Z\subseteq B^a_{11}$
and
$Z\subseteq B^a_{11}$
and
![]() $K\cap R=\emptyset $
for all
$K\cap R=\emptyset $
for all
![]() $K\in \{B^a_{12},\dots ,B^a_{1d(1)}\}$
. So
$K\in \{B^a_{12},\dots ,B^a_{1d(1)}\}$
. So
![]() $R\subseteq B^a_{11}\setminus (B^a_{12}\cup \dots \cup B^a_{1d(1)})\subseteq E(a;Y)$
.
$R\subseteq B^a_{11}\setminus (B^a_{12}\cup \dots \cup B^a_{1d(1)})\subseteq E(a;Y)$
.
Since
![]() $R\cup C_1\cup \dots \cup C_m=Z$
and
$R\cup C_1\cup \dots \cup C_m=Z$
and
![]() $|Z|\geq \frac {1}{8}|Y|$
, by Claim 3.2, we may assume that
$|Z|\geq \frac {1}{8}|Y|$
, by Claim 3.2, we may assume that
![]() $|C_1\cup \dots \cup C_{m}|\geq \frac {1}{16}|Y|$
.
$|C_1\cup \dots \cup C_{m}|\geq \frac {1}{16}|Y|$
.
Let
![]() $t_0$
be smallest such that
$t_0$
be smallest such that
![]() $|C_1\cup \dots \cup C_{t_0}|\geq \frac {1}{32}|Y|$
. Because
$|C_1\cup \dots \cup C_{t_0}|\geq \frac {1}{32}|Y|$
. Because
![]() $|C_1\cup \dots \cup C_{t_0-1}|<\frac {1}{32}|Y|$
and
$|C_1\cup \dots \cup C_{t_0-1}|<\frac {1}{32}|Y|$
and
![]() $|C_{t_0}|<\frac {1}{8}|Y|$
(by minimality of Z),
$|C_{t_0}|<\frac {1}{8}|Y|$
(by minimality of Z),
Let
![]() $C:=C_1\cup \dots \cup C_{t_0}$
.
$C:=C_1\cup \dots \cup C_{t_0}$
.
Consider
Since
![]() $A_1\cup A_2=X$
, we have
$A_1\cup A_2=X$
, we have
![]() $|A_1|\geq \frac {1}{2}|X|$
or
$|A_1|\geq \frac {1}{2}|X|$
or
![]() $|A_2|\geq \frac {1}{2}|X|$
.
$|A_2|\geq \frac {1}{2}|X|$
.
Suppose
![]() $|A_1|\geq \frac {1}{2}|X|$
. For
$|A_1|\geq \frac {1}{2}|X|$
. For
![]() $a\in A_1$
,
$a\in A_1$
,
 $$ \begin{align*} E(a,Y\setminus C)&=((B^a_{11}\setminus B^a_{12}\cup\dots\cup B^a_{1d(1)})\cap(Y\setminus C))\dot\cup\dots\\& \quad\ \dot\cup((B^a_{s_a1}\setminus B^a_{s_a2}\cup\dots\cup B^a_{s_ad(s_a)})\cap (Y\setminus C))\\&=(((B^a_{11}\cap (Y\setminus C))\setminus (B^a_{12}\cap (Y\setminus C))\cup\dots\cup (B^a_{1d(1)}\cap(Y\setminus C)))\dot\cup\dots \\& \quad\ \dot\cup(B^a_{s_a1}\cap(Y{\kern-1pt}\setminus{\kern-1pt} C))\setminus (((B^a_{s_a2}\cap(Y{\kern-1pt}\setminus{\kern-1pt} C))\cup\dots\cup (B^a_{s_ad(s_a)}\cap(Y{\kern-1pt}\setminus{\kern-1pt} C)))). \end{align*} $$
$$ \begin{align*} E(a,Y\setminus C)&=((B^a_{11}\setminus B^a_{12}\cup\dots\cup B^a_{1d(1)})\cap(Y\setminus C))\dot\cup\dots\\& \quad\ \dot\cup((B^a_{s_a1}\setminus B^a_{s_a2}\cup\dots\cup B^a_{s_ad(s_a)})\cap (Y\setminus C))\\&=(((B^a_{11}\cap (Y\setminus C))\setminus (B^a_{12}\cap (Y\setminus C))\cup\dots\cup (B^a_{1d(1)}\cap(Y\setminus C)))\dot\cup\dots \\& \quad\ \dot\cup(B^a_{s_a1}\cap(Y{\kern-1pt}\setminus{\kern-1pt} C))\setminus (((B^a_{s_a2}\cap(Y{\kern-1pt}\setminus{\kern-1pt} C))\cup\dots\cup (B^a_{s_ad(s_a)}\cap(Y{\kern-1pt}\setminus{\kern-1pt} C)))). \end{align*} $$
Since
![]() $a\in A_1$
, for some
$a\in A_1$
, for some
![]() $B^a_{kl}$
,
$B^a_{kl}$
,
![]() $B^a_{kl}\subseteq C$
. If
$B^a_{kl}\subseteq C$
. If
![]() $B^a_{kl}$
is an outer ball, say
$B^a_{kl}$
is an outer ball, say
![]() $B^a_{kl}=B^a_{11}$
, then
$B^a_{kl}=B^a_{11}$
, then
 $$ \begin{align*} E(a,Y\setminus C)&=((B^a_{21}\cap (Y\setminus C))\setminus (B^a_{22}\cap (Y\setminus C))\cup\dots\cup (B^a_{2d(2)}\cap(Y\setminus C)))\dot\cup\dots\\& \quad\ \dot\cup (B^a_{s_a1}\cap(Y\setminus C))\setminus (((B^a_{s_a2}\cap(Y\setminus C))\cup\dots\cup (B^a_{s_ad(s_a)}\cap(Y\setminus C)))). \end{align*} $$
$$ \begin{align*} E(a,Y\setminus C)&=((B^a_{21}\cap (Y\setminus C))\setminus (B^a_{22}\cap (Y\setminus C))\cup\dots\cup (B^a_{2d(2)}\cap(Y\setminus C)))\dot\cup\dots\\& \quad\ \dot\cup (B^a_{s_a1}\cap(Y\setminus C))\setminus (((B^a_{s_a2}\cap(Y\setminus C))\cup\dots\cup (B^a_{s_ad(s_a)}\cap(Y\setminus C)))). \end{align*} $$
If
![]() $B^a_{kl}$
is a hole, say
$B^a_{kl}$
is a hole, say
![]() $B^a_{kl}=B^a_{12}$
, then
$B^a_{kl}=B^a_{12}$
, then
 $$ \begin{align*} E(a,Y\setminus C)&=((B^a_{11}\cap (Y\setminus C))\setminus (B^a_{13}\cap (Y\setminus C))\cup\dots\cup (B^a_{1d(1)}\cap(Y\setminus C)))\dot\cup\dots \\& \quad\ \dot\cup(B^a_{s_a1}\cap(Y\setminus C))\setminus (((B^a_{s_a2}\cap(Y\setminus C))\cup\dots\cup (B^a_{s_ad(s_a)}\cap(Y\setminus C)))).\end{align*} $$
$$ \begin{align*} E(a,Y\setminus C)&=((B^a_{11}\cap (Y\setminus C))\setminus (B^a_{13}\cap (Y\setminus C))\cup\dots\cup (B^a_{1d(1)}\cap(Y\setminus C)))\dot\cup\dots \\& \quad\ \dot\cup(B^a_{s_a1}\cap(Y\setminus C))\setminus (((B^a_{s_a2}\cap(Y\setminus C))\cup\dots\cup (B^a_{s_ad(s_a)}\cap(Y\setminus C)))).\end{align*} $$
Hence
![]() $(A_1, Y\setminus C; E)$
is a bipartite graph of VC-minimal complexity
$(A_1, Y\setminus C; E)$
is a bipartite graph of VC-minimal complexity
![]() $<N$
such that for any
$<N$
such that for any
![]() $a\in A_1$
,
$a\in A_1$
,
![]() $E(a,Y\setminus C)$
is a disjoint union of
$E(a,Y\setminus C)$
is a disjoint union of
![]() $\Psi '$
-Swiss cheeses, where
$\Psi '$
-Swiss cheeses, where
By inductive hypothesis, there exist
![]() $F\subseteq A_1$
,
$F\subseteq A_1$
,
![]() $G\subseteq Y\setminus C$
with
$G\subseteq Y\setminus C$
with
such that
![]() $F\times G\subseteq E$
or
$F\times G\subseteq E$
or
![]() $F\times G\subseteq \neg E$
. So the conclusion holds for
$F\times G\subseteq \neg E$
. So the conclusion holds for
![]() $N+1$
.
$N+1$
.
Suppose
![]() $|A_2|\geq \frac {1}{2}|X|$
. Then
$|A_2|\geq \frac {1}{2}|X|$
. Then
![]() $\forall a\in A_2$
,
$\forall a\in A_2$
,
![]() $\forall k,l\in \mathbb {N}$
,
$\forall k,l\in \mathbb {N}$
,
![]() $B^a_{kl}\nsubseteq C$
.
$B^a_{kl}\nsubseteq C$
.
Claim 3.3.
![]() $\forall a\in A_2$
,
$\forall a\in A_2$
,
![]() $E(a,C)=\emptyset $
or
$E(a,C)=\emptyset $
or
![]() $E(a,C)=C$
.
$E(a,C)=C$
.
Proof. We first show that for all
![]() $a\in A_2$
, for all
$a\in A_2$
, for all
![]() $k,l\in \mathbb {N}$
, if
$k,l\in \mathbb {N}$
, if
![]() $B^a_{kl}\cap C\neq \emptyset $
then
$B^a_{kl}\cap C\neq \emptyset $
then
![]() $C\subseteq B^a_{kl}$
.
$C\subseteq B^a_{kl}$
.
Fix
![]() $a\in A_2$
and
$a\in A_2$
and
![]() $k,l\in \mathbb {N}$
. If
$k,l\in \mathbb {N}$
. If
![]() $B^a_{kl}\cap C\neq \emptyset $
, then
$B^a_{kl}\cap C\neq \emptyset $
, then
![]() $B^a_{kl}\cap Z\neq \emptyset $
. So
$B^a_{kl}\cap Z\neq \emptyset $
. So
![]() $B^a_{kl}\subsetneq Z$
or
$B^a_{kl}\subsetneq Z$
or
![]() $B^a_{kl}\supseteq Z$
. If
$B^a_{kl}\supseteq Z$
. If
![]() $B^a_{kl}\subsetneq Z$
, then
$B^a_{kl}\subsetneq Z$
, then
![]() $B^a_{kl}\subseteq C_t$
for some
$B^a_{kl}\subseteq C_t$
for some
![]() $t\in \{1,\dots ,m\}$
. But since
$t\in \{1,\dots ,m\}$
. But since
![]() $B^a_{kl}\nsubseteq C$
,
$B^a_{kl}\nsubseteq C$
,
![]() $B^a_{kl}\cap C=\emptyset $
, a contradiction. Hence we must have
$B^a_{kl}\cap C=\emptyset $
, a contradiction. Hence we must have
![]() $B^a_{kl}\supseteq Z$
when
$B^a_{kl}\supseteq Z$
when
![]() $B^a_{kl}\cap C\neq \emptyset $
. Thus
$B^a_{kl}\cap C\neq \emptyset $
. Thus
![]() $\forall a\in A_2$
,
$\forall a\in A_2$
,
![]() $\forall k,l\in \mathbb {N}$
,
$\forall k,l\in \mathbb {N}$
,
![]() $B^a_{kl}\cap C=\emptyset $
or
$B^a_{kl}\cap C=\emptyset $
or
![]() $B^a_{kl}\supseteq C$
.
$B^a_{kl}\supseteq C$
.
For
![]() $a\in A_2$
, if
$a\in A_2$
, if
![]() $E(a,C)\neq \emptyset $
, may assume
$E(a,C)\neq \emptyset $
, may assume
![]() $C\cap (B^a_{11}\setminus (B^a_{12}\cup \dots \cup B^a_{1d(1)}))\neq \emptyset $
. So
$C\cap (B^a_{11}\setminus (B^a_{12}\cup \dots \cup B^a_{1d(1)}))\neq \emptyset $
. So
![]() $C\cap B^a_{11}\neq \emptyset $
and
$C\cap B^a_{11}\neq \emptyset $
and
![]() $C\subseteq B^a_{11}$
. For any hole
$C\subseteq B^a_{11}$
. For any hole
![]() $K\in \{B^a_{12},\dots ,B^a_{1d(1)}\}$
, if
$K\in \{B^a_{12},\dots ,B^a_{1d(1)}\}$
, if
![]() $C\cap K\neq \emptyset $
, then
$C\cap K\neq \emptyset $
, then
![]() $C\subseteq K$
and
$C\subseteq K$
and
![]() $C\cap B^a_{11}\setminus (B^a_{12}\cup \dots \cup B^a_{1d(1)}))=\emptyset $
, a contradiction. So for any hole K,
$C\cap B^a_{11}\setminus (B^a_{12}\cup \dots \cup B^a_{1d(1)}))=\emptyset $
, a contradiction. So for any hole K,
![]() $C\cap K=\emptyset $
. Thus
$C\cap K=\emptyset $
. Thus
![]() $C\subseteq (B^a_{11}\setminus (B^a_{12}\cup \dots \cup B^a_{1d(1)}))$
. Hence
$C\subseteq (B^a_{11}\setminus (B^a_{12}\cup \dots \cup B^a_{1d(1)}))$
. Hence
![]() $\forall a\in A_2$
,
$\forall a\in A_2$
,
![]() $E(a,C)=\emptyset $
or
$E(a,C)=\emptyset $
or
![]() $E(a,C)=C$
.
$E(a,C)=C$
.
So the conclusion holds for
![]() $N+1$
(because
$N+1$
(because
![]() $|A_2|\geq \frac {1}{2}|X|$
and
$|A_2|\geq \frac {1}{2}|X|$
and
![]() $|C|\geq \frac {1}{32}|Y|$
).
$|C|\geq \frac {1}{32}|Y|$
).
4. Corollary
We can apply Theorem 3.1 to VC-minimal theories (ACVF in particular). The following notions and fact about VC-minimal theories come from [Reference Adler1]. We rephrase them as in [Reference Cotter and Starchenko7] for notational convenience.
Definition 4.1 [Reference Adler1, Definition 5][Reference Cotter and Starchenko7, Definition 2.1(1)]
A set of formulae
![]() $\Psi = \{\psi _i(x, \bar {y_i}) : i \in I\}$
is called a directed family if for any
$\Psi = \{\psi _i(x, \bar {y_i}) : i \in I\}$
is called a directed family if for any
![]() $\psi _0(x, \bar {y_0}), \psi _1(x, \bar {y_1}) \in \Psi $
and any parameters
$\psi _0(x, \bar {y_0}), \psi _1(x, \bar {y_1}) \in \Psi $
and any parameters
![]() $\bar {a_0}, \bar {a_1}$
taken from any model of T, one of the following is true:
$\bar {a_0}, \bar {a_1}$
taken from any model of T, one of the following is true:
(i):
![]() $\psi _0(x, \bar {a_0}) \subseteq \psi _1(x, \bar {a_1})$
;
$\psi _0(x, \bar {a_0}) \subseteq \psi _1(x, \bar {a_1})$
;
(ii):
![]() $\psi _1(x, \bar {a_1}) \subseteq \psi _0(x, \bar {a_0})$
;
$\psi _1(x, \bar {a_1}) \subseteq \psi _0(x, \bar {a_0})$
;
(iii):
![]() $\psi _0(x, \bar {a_0}) \cap \psi _1(x, \bar {a_1}) = \emptyset $
.
$\psi _0(x, \bar {a_0}) \cap \psi _1(x, \bar {a_1}) = \emptyset $
.
Definition 4.2 [Reference Adler1, Definition 3][Reference Cotter and Starchenko7, Definition 2.1(2)]
A theory T is VC-minimal if there is a directed family
![]() $\Psi $
such that for any formula
$\Psi $
such that for any formula
![]() $\varphi (x,\bar {y})$
and any parameters
$\varphi (x,\bar {y})$
and any parameters
![]() $\bar {c}$
taken from any model of T,
$\bar {c}$
taken from any model of T,
![]() $\varphi (x,\bar {c})$
is equivalent to a finite boolean combination of formulae
$\varphi (x,\bar {c})$
is equivalent to a finite boolean combination of formulae
![]() $\psi _i(x,\bar {b_i})$
, where each
$\psi _i(x,\bar {b_i})$
, where each
![]() $\psi _i \in \Psi $
.
$\psi _i \in \Psi $
.
Fact 4.1 [Reference Adler1, Proposition 7][Reference Cotter and Starchenko7, Theorem 2.6]
Fix T a VC-minimal theory and a directed family of formulae
![]() $\Psi $
for T. For every formula
$\Psi $
for T. For every formula
![]() $\tau (x,\bar {y})$
, there are a finite set
$\tau (x,\bar {y})$
, there are a finite set
![]() $\Psi _0 \subseteq \Psi $
and natural numbers
$\Psi _0 \subseteq \Psi $
and natural numbers
![]() $n_1$
and
$n_1$
and
![]() $n_2$
such that for every parameter tuple
$n_2$
such that for every parameter tuple
![]() $\bar {a}$
,
$\bar {a}$
,
![]() $\tau (x,\bar {a})$
can be decomposed as the union of at most
$\tau (x,\bar {a})$
can be decomposed as the union of at most
![]() $n_1$
disjoint Swiss cheeses, each of them having at most
$n_1$
disjoint Swiss cheeses, each of them having at most
![]() $n_2$
holes, such that all balls appearing in the decomposition are instances of formulae in
$n_2$
holes, such that all balls appearing in the decomposition are instances of formulae in
![]() $\Psi _0$
.
$\Psi _0$
.
By Fact 4.1, for any VC-minimal theory T, any model
![]() $\mathcal {M}\models T$
and any definable relation
$\mathcal {M}\models T$
and any definable relation
![]() $E(x,\bar {y})\subseteq M\times M^{|\bar {y}|}$
, there is
$E(x,\bar {y})\subseteq M\times M^{|\bar {y}|}$
, there is
![]() $N\in \mathbb {N}^{>0}$
such that for any finite disjoint
$N\in \mathbb {N}^{>0}$
such that for any finite disjoint
![]() $X,Y\subseteq M$
, the bipartite graph
$X,Y\subseteq M$
, the bipartite graph
![]() $(X,Y;E)$
has VC-minimal complexity
$(X,Y;E)$
has VC-minimal complexity
![]() $<N$
. Thus we have the following:
$<N$
. Thus we have the following:
Corollary 4.1.1. Given a VC-minimal theory T, a model
![]() $\mathcal {M}\models T$
and an
$\mathcal {M}\models T$
and an
![]() $\mathcal {L}$
-formula
$\mathcal {L}$
-formula
![]() $\varphi (x,\bar {y},\bar {z})$
, let
$\varphi (x,\bar {y},\bar {z})$
, let
![]() $N\in \mathbb {N}^{>0}$
satisfy: for any
$N\in \mathbb {N}^{>0}$
satisfy: for any
![]() $\bar {b}\in M^{|\bar {y}|}$
,
$\bar {b}\in M^{|\bar {y}|}$
,
![]() $\bar {c}\in M^{|\bar {z}|}$
,
$\bar {c}\in M^{|\bar {z}|}$
,
![]() $\varphi (x,\bar {b},\bar {c})$
can be decomposed as the union of at most
$\varphi (x,\bar {b},\bar {c})$
can be decomposed as the union of at most
![]() $n_1$
disjoint Swiss cheeses, each of them having at most
$n_1$
disjoint Swiss cheeses, each of them having at most
![]() $n_2$
holes, with
$n_2$
holes, with
![]() $n_1n_2<N$
. Then for any fixed
$n_1n_2<N$
. Then for any fixed
![]() $\bar {c}\in M^{|\bar {z}|}$
, any pair of finite sets
$\bar {c}\in M^{|\bar {z}|}$
, any pair of finite sets
![]() $X\subseteq M$
,
$X\subseteq M$
,
![]() $Y\subseteq M^{|\bar {y}|}$
, there exist
$Y\subseteq M^{|\bar {y}|}$
, there exist
![]() $X'\subseteq X$
,
$X'\subseteq X$
,
![]() $Y'\subseteq Y$
such that
$Y'\subseteq Y$
such that
![]() $|X'|\geq \dfrac {1}{2^{N+4}}|X|$
,
$|X'|\geq \dfrac {1}{2^{N+4}}|X|$
,
![]() $Y'\geq \dfrac {1}{2^{N+4}}|Y|$
, and
$Y'\geq \dfrac {1}{2^{N+4}}|Y|$
, and
![]() $\forall x\in X'$
$\forall x\in X'$
![]() $\forall \bar {y}\in Y'$
$\forall \bar {y}\in Y'$
![]() $\varphi (x,\bar {y},\bar {c})$
or
$\varphi (x,\bar {y},\bar {c})$
or
![]() $\forall x\in X'$
$\forall x\in X'$
![]() $\forall \bar {y}\in Y'$
$\forall \bar {y}\in Y'$
![]() $\neg \varphi (x,\bar {y},\bar {c})$
.
$\neg \varphi (x,\bar {y},\bar {c})$
.
Remark ([Reference Chernikov and Starchenko4, Example 4.11(2)] shows)
Let
![]() $\mathcal {M}\models ACVF_{0,0}$
and let a formula
$\mathcal {M}\models ACVF_{0,0}$
and let a formula
![]() $\varphi (\bar {x}, \bar {y},\bar {z})$
be given. Then there is some
$\varphi (\bar {x}, \bar {y},\bar {z})$
be given. Then there is some
![]() $\delta = \delta (\varphi )> 0$
such that for any definable relation
$\delta = \delta (\varphi )> 0$
such that for any definable relation
![]() $E(\bar {x}, \bar {y}) = \varphi (\bar {x}, \bar {y},\bar {c})$
for some
$E(\bar {x}, \bar {y}) = \varphi (\bar {x}, \bar {y},\bar {c})$
for some
![]() $\bar {c}\in M^{|\bar {z}|}$
and finite disjoint
$\bar {c}\in M^{|\bar {z}|}$
and finite disjoint
![]() $X\subseteq M^{|\bar {x}|}$
,
$X\subseteq M^{|\bar {x}|}$
,
![]() $Y\subseteq M^{|\bar {y}|}$
, there are some
$Y\subseteq M^{|\bar {y}|}$
, there are some
![]() $X'\subseteq X$
,
$X'\subseteq X$
,
![]() $Y'\subseteq Y$
with
$Y'\subseteq Y$
with
![]() $|X'| \geq \delta |X|$
,
$|X'| \geq \delta |X|$
,
![]() $|Y'|\geq \delta |Y|$
and
$|Y'|\geq \delta |Y|$
and
![]() $X'\times Y'\subseteq E$
or
$X'\times Y'\subseteq E$
or
![]() $X'\times Y'\subseteq \neg E$
. By [Reference Holly11],
$X'\times Y'\subseteq \neg E$
. By [Reference Holly11],
![]() $ACVF$
has Swiss Cheese decomposition and thus is a VC-minimal theory. So by Corollary 4.1.1, the same conclusion also holds in
$ACVF$
has Swiss Cheese decomposition and thus is a VC-minimal theory. So by Corollary 4.1.1, the same conclusion also holds in
![]() $ACVF_{p,q}$
for nonzero
$ACVF_{p,q}$
for nonzero
![]() $p,q$
when
$p,q$
when
![]() $|\bar {x}|=1$
.
$|\bar {x}|=1$
.
Note: [Reference Chernikov and Starchenko4, Example 4.11(2)] allows
![]() $|\bar {x}|>1$
and
$|\bar {x}|>1$
and
![]() $|\bar {y}|>1$
for definable relations
$|\bar {y}|>1$
for definable relations
![]() $E(\bar {x},\bar {y})$
in
$E(\bar {x},\bar {y})$
in
![]() $ACVF_{0,0}$
. But for positive characteristics, when
$ACVF_{0,0}$
. But for positive characteristics, when
![]() $|\bar {x}|>1$
,
$|\bar {x}|>1$
,
![]() $|\bar {y}|>1$
, there is a counter example given in [Reference Chernikov and Starchenko4, Proposition 6.2]:
$|\bar {y}|>1$
, there is a counter example given in [Reference Chernikov and Starchenko4, Proposition 6.2]:
Fact 4.2 [Reference Chernikov and Starchenko4, Proposition 6.2]
Let
![]() $p>0$
, and let
$p>0$
, and let
![]() $\mathbb {F}= \mathbb {F}_p^{alg}$
. For a set of points
$\mathbb {F}= \mathbb {F}_p^{alg}$
. For a set of points
![]() $P \subseteq \mathbb {F}^2$
and a set of lines L in
$P \subseteq \mathbb {F}^2$
and a set of lines L in
![]() $\mathbb {F}^2$
we denote by
$\mathbb {F}^2$
we denote by
![]() $I(P,L) \subseteq P \times L$
the incidence relation, i.e.,
$I(P,L) \subseteq P \times L$
the incidence relation, i.e.,
![]() $I(P,L) = \{(p,l) \in P \times L : p \in l\}$
. Then for all constants
$I(P,L) = \{(p,l) \in P \times L : p \in l\}$
. Then for all constants
![]() $\delta> 0$
, there exist a finite (sufficiently large) set of points
$\delta> 0$
, there exist a finite (sufficiently large) set of points
![]() $P \subseteq \mathbb {F}^2$
and a finite (sufficiently large) set of lines L in
$P \subseteq \mathbb {F}^2$
and a finite (sufficiently large) set of lines L in
![]() $\mathbb {F}^2$
such that for all
$\mathbb {F}^2$
such that for all
![]() $P_0 \subseteq P$
and
$P_0 \subseteq P$
and
![]() $L_0 \subseteq L$
with
$L_0 \subseteq L$
with
![]() $|P_0| \geq \delta |P|$
,
$|P_0| \geq \delta |P|$
,
![]() $|L_0| \geq \delta |L|$
,
$|L_0| \geq \delta |L|$
,
![]() $I(P_0,L_0) \neq \emptyset $
.
$I(P_0,L_0) \neq \emptyset $
.
Thus the strong Erdős–Hajnal property fails for I in
![]() $\mathbb {F}$
and we cannot generalize Corollary 4.1.1 to the case where both
$\mathbb {F}$
and we cannot generalize Corollary 4.1.1 to the case where both
![]() $|\bar {x}|>1$
and
$|\bar {x}|>1$
and
![]() $|\bar {y}|>1$
.
$|\bar {y}|>1$
.
Remark. In [Reference Chudnovsky, Scott, Seymour and Spirkl6], Chudnovsky, Scott, Seymour, and Spirkl proved the following fact:
Fact 4.3 [Reference Chudnovsky, Scott, Seymour and Spirkl6, 1.2]
For every forest H, there exists
![]() $\epsilon> 0$
such that for every graph G with
$\epsilon> 0$
such that for every graph G with
![]() $|G|> 1$
that is both H-free and
$|G|> 1$
that is both H-free and
![]() $\overline {H}$
-free, there is a pair of disjoint subsets
$\overline {H}$
-free, there is a pair of disjoint subsets
![]() $(A, B)$
with
$(A, B)$
with
![]() $|A|, |B| \geq \epsilon |G|$
such that
$|A|, |B| \geq \epsilon |G|$
such that
![]() $A\times B\subseteq E$
or
$A\times B\subseteq E$
or
![]() $A\times B\cap E=\emptyset $
.
$A\times B\cap E=\emptyset $
.
The family of forests can be shown to have VC-minimal complexity
![]() $\leq 2$
and thus the VC-minimal case is not covered in [Reference Chudnovsky, Scott, Seymour and Spirkl6].
$\leq 2$
and thus the VC-minimal case is not covered in [Reference Chudnovsky, Scott, Seymour and Spirkl6].
For a forest H,
![]() $v\in V(H)$
, let
$v\in V(H)$
, let
![]() $B_{v,\triangleleft }$
denote the set of the predecessor of v and
$B_{v,\triangleleft }$
denote the set of the predecessor of v and
![]() $B_{v,\triangleright }$
denote the set of successors of v. Consider the family
$B_{v,\triangleright }$
denote the set of successors of v. Consider the family
![]() $\mathcal {F}_{H}:=$
$\mathcal {F}_{H}:=$
![]() $\{B_{v,\triangleleft }, B_{v,\triangleright }: v\in H\}$
.
$\{B_{v,\triangleleft }, B_{v,\triangleright }: v\in H\}$
.
![]() $\mathcal {F}_H$
is directed: Let
$\mathcal {F}_H$
is directed: Let
![]() $v, w\in V(H)$
. If
$v, w\in V(H)$
. If
![]() $B_{v,\triangleleft }\cap B_{w,\triangleright }\neq \emptyset $
, then since
$B_{v,\triangleleft }\cap B_{w,\triangleright }\neq \emptyset $
, then since
![]() $B_{v,\triangleleft }$
is a singleton,
$B_{v,\triangleleft }$
is a singleton,
![]() $B_{v,\triangleleft }\subseteq B_{w,\triangleright }$
. Similarly, if
$B_{v,\triangleleft }\subseteq B_{w,\triangleright }$
. Similarly, if
![]() $B_{v,\triangleleft }\cap B_{w,\triangleleft }\neq \emptyset $
, then
$B_{v,\triangleleft }\cap B_{w,\triangleleft }\neq \emptyset $
, then
![]() $B_{v,\triangleleft }\subseteq B_{w,\triangleleft }$
. If
$B_{v,\triangleleft }\subseteq B_{w,\triangleleft }$
. If
![]() $B_{v,\triangleright }\cap B_{w,\triangleright }\neq \emptyset $
, then
$B_{v,\triangleright }\cap B_{w,\triangleright }\neq \emptyset $
, then
![]() $v=w$
and
$v=w$
and
![]() $B_{v,\triangleright }= B_{w,\triangleright }$
.
$B_{v,\triangleright }= B_{w,\triangleright }$
.
For any
![]() $v\in V(H)$
,
$v\in V(H)$
,
![]() $E_v=B_{v,\triangleleft } \sqcup B_{v,\triangleright }$
. So given any forest
$E_v=B_{v,\triangleleft } \sqcup B_{v,\triangleright }$
. So given any forest
![]() $H=(V(H),E)$
and disjoint
$H=(V(H),E)$
and disjoint
![]() $X,Y\subseteq V(H)$
, the bipartite graph
$X,Y\subseteq V(H)$
, the bipartite graph
![]() $(X,Y;E)$
has VC-minimal complexity
$(X,Y;E)$
has VC-minimal complexity
![]() $\leq 2$
.
$\leq 2$
.
Acknowledgments
The author is grateful to her advisor Sergei Starchenko and the referee for reading the paper and giving helpful suggestions.
Funding
The author was partially supported by the NSF research grant DMS-1800806.