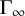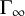1 Introduction
Let V be an algebraic variety over a rank 1 nonarchimedean field K. There are two well-behaved cohomology theories that can be attached to the analytification
![]() $V^{\mathrm {an}}$
of V in the sense of V. Berkovich: the singular cohomology and the étale cohomology. Both have been proven to carry interesting information about V (see [Reference Berkovich12], [Reference Berkovich9], [Reference Berkovich10], to cite just a few).
$V^{\mathrm {an}}$
of V in the sense of V. Berkovich: the singular cohomology and the étale cohomology. Both have been proven to carry interesting information about V (see [Reference Berkovich12], [Reference Berkovich9], [Reference Berkovich10], to cite just a few).
When K is a nonarchimedean field of higher rank, E. Hrushovski and F. Loeser [Reference Hrushovski and Loeser35] introduced a topological space
![]() $\widehat {V}(K)$
called the stable completion of V, which can be thought as a higher-rank analogue of Berkovich’s analytification. If V is a quasi-projective variety, the main theorem in [Reference Hrushovski and Loeser35] shows a very deep connection between
$\widehat {V}(K)$
called the stable completion of V, which can be thought as a higher-rank analogue of Berkovich’s analytification. If V is a quasi-projective variety, the main theorem in [Reference Hrushovski and Loeser35] shows a very deep connection between
![]() $\widehat {V}(K)$
and the tropical semi-group
$\widehat {V}(K)$
and the tropical semi-group
![]() $\Gamma _{\infty }$
associated to the value group
$\Gamma _{\infty }$
associated to the value group
![]() $\Gamma $
of K: there is a deformation retraction from
$\Gamma $
of K: there is a deformation retraction from
![]() $\widehat {V}(K)$
to a piece-wise semi-linear subset of a finite power of
$\widehat {V}(K)$
to a piece-wise semi-linear subset of a finite power of
![]() $\Gamma _{\infty }$
. An analogous result was earlier proved by Berkovich [Reference Berkovich11] for
$\Gamma _{\infty }$
. An analogous result was earlier proved by Berkovich [Reference Berkovich11] for
![]() $V^{\mathrm {an}}$
under strong algebraic restrictions on V.
$V^{\mathrm {an}}$
under strong algebraic restrictions on V.
The aim of this article is to introduce a well-behaved cohomology theory of the space
![]() $\widehat {V}(K)$
that coincides with the singular cohomology when K has rank 1. In particular, we show our cohomology satisfies finiteness and invariance and has natural bounds on the cohomological dimension. As an application of the above, we extend results of Berkovich on the singular cohomology and obtain a tameness result in families showing there are only finitely many cohomology groups in fibres.
$\widehat {V}(K)$
that coincides with the singular cohomology when K has rank 1. In particular, we show our cohomology satisfies finiteness and invariance and has natural bounds on the cohomological dimension. As an application of the above, we extend results of Berkovich on the singular cohomology and obtain a tameness result in families showing there are only finitely many cohomology groups in fibres.
Typically (e.g., when K has rank bigger than one), the underlying topological space of
![]() $\widehat {V}(K)$
is not even locally compact (see later Remark 7.5). We bypass such a problem by introducing a suitable site on
$\widehat {V}(K)$
is not even locally compact (see later Remark 7.5). We bypass such a problem by introducing a suitable site on
![]() $\widehat {V}(K)$
(the
$\widehat {V}(K)$
(the
![]() $\widehat {\mathrm {v\!+\!g}}$
-site) and using a formalism of sheaves developed by M. Edmundo and L. Prelli ([Reference Edmundo and Prelli27]), which builds on a modification of M. Kashiwara and P. Schapira’s ([Reference Kashiwara and Schapira40]). Recent applications such as [Reference Bakker, Brunenarbe and Tsimerman2] and [Reference Benoist and Wittenberg5, Reference Benoist and Wittenberg6] are implicitly working within this formalism.
$\widehat {\mathrm {v\!+\!g}}$
-site) and using a formalism of sheaves developed by M. Edmundo and L. Prelli ([Reference Edmundo and Prelli27]), which builds on a modification of M. Kashiwara and P. Schapira’s ([Reference Kashiwara and Schapira40]). Recent applications such as [Reference Bakker, Brunenarbe and Tsimerman2] and [Reference Benoist and Wittenberg5, Reference Benoist and Wittenberg6] are implicitly working within this formalism.
Our approach is reminiscent of J. Tate’s initial attempt to study rigid analytic spaces via G-topologies [Reference Tate52]. However, it is worthwhile to mention that, in contrast with cohomology theories defined via the analytification of algebraic varieties, our definition is intrinsically algebraic and makes no use of Tate algebras or affinoid domains. This confirms Hrushovski-Loeser’s idea that a ‘rigid algebraic geometry exists as well’ (see [Reference Hrushovski and Loeser35, Chapter 1]).
2 Main results
2.1 Cohomology theories
Let K be an algebraically closed nonarchimedean field of arbitrary rank,
![]() $\Gamma $
be its value group and
$\Gamma $
be its value group and
![]() $\Gamma _{\infty }=\Gamma \cup \{\infty \}$
the associated tropical semi-group. In order to fully exploit Hrushovski-Loeser’s main theorem, part of the present article consists in developing in parallel a sheaf cohomology of definable (i.e., semi-linear) sets of
$\Gamma _{\infty }=\Gamma \cup \{\infty \}$
the associated tropical semi-group. In order to fully exploit Hrushovski-Loeser’s main theorem, part of the present article consists in developing in parallel a sheaf cohomology of definable (i.e., semi-linear) sets of
![]() $\Gamma _{\infty }$
. More generally, we lay out a sheaf cohomology for definable sets in o-minimal expansions of
$\Gamma _{\infty }$
. More generally, we lay out a sheaf cohomology for definable sets in o-minimal expansions of
![]() $\Gamma _{\infty }$
over the site of open definable sets, extending theorems from [Reference Edmundo, Jones and Peatfield22, Reference Edmundo and Prelli25, Reference Edmundo and Prelli26, Reference Edmundo and Prelli28] on sheaves on o-minimal expansions of
$\Gamma _{\infty }$
over the site of open definable sets, extending theorems from [Reference Edmundo, Jones and Peatfield22, Reference Edmundo and Prelli25, Reference Edmundo and Prelli26, Reference Edmundo and Prelli28] on sheaves on o-minimal expansions of
![]() $\Gamma $
, including the formalism of the six Grothendieck operations (see Remark 6.23). It is worth mentioning that the passage from
$\Gamma $
, including the formalism of the six Grothendieck operations (see Remark 6.23). It is worth mentioning that the passage from
![]() $\Gamma $
to
$\Gamma $
to
![]() $\Gamma _{\infty }$
is more subtle than one might expect, as already noted by Hrushovski and Loeser (see the first paragraph in [Reference Hrushovski and Loeser35, Section 4.1]).
$\Gamma _{\infty }$
is more subtle than one might expect, as already noted by Hrushovski and Loeser (see the first paragraph in [Reference Hrushovski and Loeser35, Section 4.1]).
The following is the main theorem concerning our cohomology theories:
Main theorem. For algebraic varieties (possibly over a subfield of K), their stable completions and definable subsets of
![]() $\Gamma _{\infty }$
, the corresponding cohomology theory satisfies:
$\Gamma _{\infty }$
, the corresponding cohomology theory satisfies:
2.2 Applications
We obtain the following applications:
(I) In rank 1, Hrushovski and Loeser show finiteness of homotopy types in definable families (see [Reference Hrushovski and Loeser35, Theorems 14.3.1 and 14.4.4]). As they observed (see the beginning of [Reference Hrushovski and Loeser35, Section 14.3]), such a result is no longer true in higher ranks. However, using invariance of cohomology with definably compact support, we obtain a tameness result showing that given a definable family
![]() $Z_w$
of
$Z_w$
of
![]() $\mathrm {v\!+\!g}$
-locally closed subsets of a variety, as w runs through W, there are finitely many isomorphisms types for the
$\mathrm {v\!+\!g}$
-locally closed subsets of a variety, as w runs through W, there are finitely many isomorphisms types for the
![]() $\widehat {\mathrm {v\!+\!g}}$
-cohomology
$\widehat {\mathrm {v\!+\!g}}$
-cohomology
![]() $H^*_c(\widehat {Z}_{w};{\mathbb Q})$
with definably compact supports. (See later Theorem 8.1.)
$H^*_c(\widehat {Z}_{w};{\mathbb Q})$
with definably compact supports. (See later Theorem 8.1.)
Results of A. Abbes and T. Saito [Reference Abbes and Saito1], later generalised by J. Poineau [Reference Poineau48], showed that for families parametrised by the norm of an analytic function, there is a finite partition of
![]() $\mathbb {R}$
into intervals such that on each piece,
$\mathbb {R}$
into intervals such that on each piece,
![]() $\pi _0$
of the fibres are in canonical bijections. For definable families parametrised by
$\pi _0$
of the fibres are in canonical bijections. For definable families parametrised by
![]() ${\Gamma _{\infty } }$
, we get analogues of such results for
${\Gamma _{\infty } }$
, we get analogues of such results for
![]() $H_c^*$
and
$H_c^*$
and
![]() $\pi _0^{\mathrm {def}}$
(both independently of the rank). See Corollaries 8.2 and 8.3.
$\pi _0^{\mathrm {def}}$
(both independently of the rank). See Corollaries 8.2 and 8.3.
It is worth pointing out that assuming finiteness and invariance of cohomology without support, similar methods lead to bounds on the
![]() $\mathrm {v\!+\!g}$
-Betti numbers of a uniformly definable family of
$\mathrm {v\!+\!g}$
-Betti numbers of a uniformly definable family of
![]() $\mathrm {v\!+\!g}$
-locally closed subsets of a variety. Such a result will be an analogue, in all ranks, of a result obtained by S. Basu and D. Patel ([Reference Basu and Patel4, Theorem 2]) in the case where the valued field has rank one, using the usual topological (singular) Betti numbers instead. In comparison with [Reference Basu and Patel4, Theorem 2], this approach will provide a much simpler proof by taking advantage of the fact that we can work in higher elementary extensions where we can endow the tropical semi-group
$\mathrm {v\!+\!g}$
-locally closed subsets of a variety. Such a result will be an analogue, in all ranks, of a result obtained by S. Basu and D. Patel ([Reference Basu and Patel4, Theorem 2]) in the case where the valued field has rank one, using the usual topological (singular) Betti numbers instead. In comparison with [Reference Basu and Patel4, Theorem 2], this approach will provide a much simpler proof by taking advantage of the fact that we can work in higher elementary extensions where we can endow the tropical semi-group
![]() ${\mathbf {\Gamma }_{\infty } }$
with the structure of a real closed field and therefore apply earlier results of Basu himself on bounds in o-minimal expansions of real closed fields ([Reference Basu3, Theorem 2.2]).
${\mathbf {\Gamma }_{\infty } }$
with the structure of a real closed field and therefore apply earlier results of Basu himself on bounds in o-minimal expansions of real closed fields ([Reference Basu3, Theorem 2.2]).
(II) We recover results of Berkovich [Reference Berkovich11] on the singular cohomology of
![]() $V^{\mathrm {an}}$
concerning finiteness and invariance (see later Theorems 7.12 and 7.13 and Corollaries 7.19 and 7.17).
$V^{\mathrm {an}}$
concerning finiteness and invariance (see later Theorems 7.12 and 7.13 and Corollaries 7.19 and 7.17).
(III) We extend Berkovich’s results in two different ways that we briefly explain. Let F be a nonarchimedean field of rank 1 (not necessarily complete) and V be an algebraic variety over F. Hrushovski and Loeser also introduced a topological space, called the model-theoretic Berkovich space associated to V, which they denoted by
![]() $B_{\mathbf F}(V)$
(see later Section 7 for its formal definition). When F is complete,
$B_{\mathbf F}(V)$
(see later Section 7 for its formal definition). When F is complete,
![]() $B_{\mathbf F}(V)$
is homeomorphic to the underlying topological space of
$B_{\mathbf F}(V)$
is homeomorphic to the underlying topological space of
![]() $V^{\mathrm {an}}$
. Letting
$V^{\mathrm {an}}$
. Letting
![]() $F^{\max }$
be a maximally complete algebraically closed extension of F with value group
$F^{\max }$
be a maximally complete algebraically closed extension of F with value group
![]() $\mathbb {R}$
, they show the existence of a closed continuous surjection
$\mathbb {R}$
, they show the existence of a closed continuous surjection
![]() $\pi \colon \widehat {V}(F^{\max })\to B_{\mathbf F}(V)$
. Such a map allowed them to transfer results from
$\pi \colon \widehat {V}(F^{\max })\to B_{\mathbf F}(V)$
. Such a map allowed them to transfer results from
![]() $\widehat {V}(F^{\max })$
to
$\widehat {V}(F^{\max })$
to
![]() $B_{\mathbf F}(V)$
and draw conclusions about the homotopy type of
$B_{\mathbf F}(V)$
and draw conclusions about the homotopy type of
![]() $V^{\mathrm {an}}$
for V quasi-projective. When
$V^{\mathrm {an}}$
for V quasi-projective. When
![]() $F=F^{\max }$
, the topological spaces
$F=F^{\max }$
, the topological spaces
![]() $\widehat {V}(F)$
,
$\widehat {V}(F)$
,
![]() $B_{\mathbf F}(V)$
and
$B_{\mathbf F}(V)$
and
![]() $V^{\mathrm {an}}$
are all homeomorphic, and we show that, in this particular case, our cohomology coincides with the singular cohomology of
$V^{\mathrm {an}}$
are all homeomorphic, and we show that, in this particular case, our cohomology coincides with the singular cohomology of
![]() $V^{\mathrm {an}}$
(Theorems 7.16 and 7.18). Furthermore, the map
$V^{\mathrm {an}}$
(Theorems 7.16 and 7.18). Furthermore, the map
![]() $\pi $
allowed us to transfer results from the
$\pi $
allowed us to transfer results from the
![]() $\widehat {\mathrm {v\!+\!g}}$
-cohomology on
$\widehat {\mathrm {v\!+\!g}}$
-cohomology on
![]() $\widehat {V}(F^{\max })$
to the singular cohomology of
$\widehat {V}(F^{\max })$
to the singular cohomology of
![]() $B_{\mathbf F}(V)$
and hence, when F is complete, to the singular cohomology of
$B_{\mathbf F}(V)$
and hence, when F is complete, to the singular cohomology of
![]() $V^{\mathrm {an}}$
. This is mainly how we recover Berkovich’s results. However, note that our results hold more generally for
$V^{\mathrm {an}}$
. This is mainly how we recover Berkovich’s results. However, note that our results hold more generally for
![]() $B_{\mathbf F}(V)$
, a space that is well-defined without assuming F to be complete.
$B_{\mathbf F}(V)$
, a space that is well-defined without assuming F to be complete.
A second way in which we extend Berkovich’s results is that our theorems actually hold for semi-algebraic subsets of
![]() $B_{\mathbf F}(V)$
(respectively, for semi-algebraic subsets of
$B_{\mathbf F}(V)$
(respectively, for semi-algebraic subsets of
![]() $\widehat {V}(K)$
, for any nontrivially valued algebraically closed field extension of F). Here, a semi-algebraic subset should be understood in the sense of A. Ducros [Reference Ducros20] (see later Fact 7.1). Using that
$\widehat {V}(K)$
, for any nontrivially valued algebraically closed field extension of F). Here, a semi-algebraic subset should be understood in the sense of A. Ducros [Reference Ducros20] (see later Fact 7.1). Using that
![]() $\widehat {V}(K)$
has finitely many definably connected components (Lemma 5.21), we also recover the analogue result due to Ducros [Reference Ducros20] for
$\widehat {V}(K)$
has finitely many definably connected components (Lemma 5.21), we also recover the analogue result due to Ducros [Reference Ducros20] for
![]() $V^{\mathrm {an}}$
. In a similar vein, but using completely different methods, F. Martin [Reference Martin43] extended results of Berkovich concerning the étale cohomology of analytic spaces to the larger category of their semi-algebraic subsets. We would like to explore in subsequent research if the techniques here employed can also be used to develop an analogue of the étale cohomology over the spaces
$V^{\mathrm {an}}$
. In a similar vein, but using completely different methods, F. Martin [Reference Martin43] extended results of Berkovich concerning the étale cohomology of analytic spaces to the larger category of their semi-algebraic subsets. We would like to explore in subsequent research if the techniques here employed can also be used to develop an analogue of the étale cohomology over the spaces
![]() $\widehat {V}(K)$
and
$\widehat {V}(K)$
and
![]() $B_{\mathbf F}(V)$
.
$B_{\mathbf F}(V)$
.
2.3 Layout of the article
Throughout, we will use a formalism of sheaves developed by M. Edmundo and L. Prelli ([Reference Edmundo and Prelli27]), which builds on a modification of M. Kashiwara and P. Schapira’s ([Reference Kashiwara and Schapira40]) notion of
![]() ${\mathcal {T}}$
-topology (a Grothendieck topology). The semi-algebraic site, the sub-analytic site, the o-minimal site and the
${\mathcal {T}}$
-topology (a Grothendieck topology). The semi-algebraic site, the sub-analytic site, the o-minimal site and the
![]() $\widehat {\mathrm {v\!+\!g}}$
-site mentioned above will be examples of such
$\widehat {\mathrm {v\!+\!g}}$
-site mentioned above will be examples of such
![]() ${\mathcal {T}}$
-topologies. The needed background and properties of such a formalism are presented in Section 3.
${\mathcal {T}}$
-topologies. The needed background and properties of such a formalism are presented in Section 3.
The novelty here is the introduction of the notions of
![]() ${\mathcal {T}}$
-normality and families of
${\mathcal {T}}$
-normality and families of
![]() ${\mathcal {T}}$
-normal supports on spaces equipped with a
${\mathcal {T}}$
-normal supports on spaces equipped with a
![]() ${\mathcal {T}}$
-topology. When we pass to the
${\mathcal {T}}$
-topology. When we pass to the
![]() ${\mathcal {T}}$
-spectrum of such Grothendieck topologies, the corresponding categories of sheaves are isomorphic, and we get normal spectral spaces (respectively, families of normal and constructible supports on such spectral spaces). The latter notion will play the role that paracompactifying families of supports plays in sheaf theory in topological spaces. We study the notion of
${\mathcal {T}}$
-spectrum of such Grothendieck topologies, the corresponding categories of sheaves are isomorphic, and we get normal spectral spaces (respectively, families of normal and constructible supports on such spectral spaces). The latter notion will play the role that paracompactifying families of supports plays in sheaf theory in topological spaces. We study the notion of
![]() $\Phi $
-soft sheaves when
$\Phi $
-soft sheaves when
![]() $\Phi $
is a normal and constructible family of supports and set up the tools required to obtain the Base change formula, the Vietoris-Begle theorem and, in Section 6, Mayer-Vietoris sequences and bounds on cohomological
$\Phi $
is a normal and constructible family of supports and set up the tools required to obtain the Base change formula, the Vietoris-Begle theorem and, in Section 6, Mayer-Vietoris sequences and bounds on cohomological
![]() $\Phi $
-dimension. These results were already known in the o-minimal case ([Reference Edmundo and Prelli25]) and the semi-algebraic case ([Reference Delfs17]), where
$\Phi $
-dimension. These results were already known in the o-minimal case ([Reference Edmundo and Prelli25]) and the semi-algebraic case ([Reference Delfs17]), where
![]() ${\mathcal {T}}$
-normality and families of
${\mathcal {T}}$
-normality and families of
![]() ${\mathcal {T}}$
-normal supports correspond to definably normal definable spaces and families of definably normal supports (respectively, regular and paracompact (locally) semi-algebraic spaces and paracompactifying (locally) semi-algebraic families of supports). Here we present a unifying approach to this theory.
${\mathcal {T}}$
-normal supports correspond to definably normal definable spaces and families of definably normal supports (respectively, regular and paracompact (locally) semi-algebraic spaces and paracompactifying (locally) semi-algebraic families of supports). Here we present a unifying approach to this theory.
In Section 4, we define the o-minimal site on a definable set in an o-minimal expansion
![]() ${\mathbf {\Gamma }_{\infty } }$
of
${\mathbf {\Gamma }_{\infty } }$
of
![]() ${\Gamma _{\infty } }$
and recall the notions of definable connectedness and definable compactness. Moreover, in order to be able to apply the tools of Section 3, we study the notion of definable normality in
${\Gamma _{\infty } }$
and recall the notions of definable connectedness and definable compactness. Moreover, in order to be able to apply the tools of Section 3, we study the notion of definable normality in
![]() ${\mathbf {\Gamma }_{\infty } }$
. Unlike in o-minimal expansions
${\mathbf {\Gamma }_{\infty } }$
. Unlike in o-minimal expansions
![]() ${\mathbf {\Gamma }}$
of
${\mathbf {\Gamma }}$
of
![]() ${\Gamma }$
, in
${\Gamma }$
, in
![]() ${\mathbf {\Gamma }_{\infty } }$
there are open definable sets that are not definably normal. The main result of Section 4, which ensures that we can later apply the tools of Section 3, is Theorem 4.28, showing that every definably locally closed set in
${\mathbf {\Gamma }_{\infty } }$
there are open definable sets that are not definably normal. The main result of Section 4, which ensures that we can later apply the tools of Section 3, is Theorem 4.28, showing that every definably locally closed set in
![]() ${\mathbf {\Gamma }_{\infty } }$
is the union of finitely many relatively open definable subsets that are definably normal. The proof of this result is rather long and is based in ideas from [Reference Edmundo and Prelli28].
${\mathbf {\Gamma }_{\infty } }$
is the union of finitely many relatively open definable subsets that are definably normal. The proof of this result is rather long and is based in ideas from [Reference Edmundo and Prelli28].
The
![]() $\widehat {\mathrm {v\!+\!g}}$
-site on the stable completion
$\widehat {\mathrm {v\!+\!g}}$
-site on the stable completion
![]() $\widehat {V}(K)$
of an algebraic variety V over an algebraically closed nonarchimedean field K (and more generally on the stable completion
$\widehat {V}(K)$
of an algebraic variety V over an algebraically closed nonarchimedean field K (and more generally on the stable completion
![]() $\widehat {X}$
of a definable subset
$\widehat {X}$
of a definable subset
![]() $X\subseteq V\times \Gamma _{\infty }^m$
) is defined and studied in Section 5. Here, for the reader’s convenience, we recall some background from [Reference Hrushovski and Loeser35] on stable completions and the notions of definable connectedness and definable compactness. In particular, we include a proof (missing in [Reference Hrushovski and Loeser35]) of the fact that the stable completion
$X\subseteq V\times \Gamma _{\infty }^m$
) is defined and studied in Section 5. Here, for the reader’s convenience, we recall some background from [Reference Hrushovski and Loeser35] on stable completions and the notions of definable connectedness and definable compactness. In particular, we include a proof (missing in [Reference Hrushovski and Loeser35]) of the fact that the stable completion
![]() $\widehat {X}$
of a definable subset
$\widehat {X}$
of a definable subset
![]() $X\subseteq V\times {\Gamma ^n_{\infty } }$
has finitely many definably connected components (Lemma 5.21). The main result of this section is Corollary 5.31 showing that if X is a
$X\subseteq V\times {\Gamma ^n_{\infty } }$
has finitely many definably connected components (Lemma 5.21). The main result of this section is Corollary 5.31 showing that if X is a
![]() $\mathrm {v\!+\!g}$
-locally closed subset, then X is the union of finitely many basic
$\mathrm {v\!+\!g}$
-locally closed subset, then X is the union of finitely many basic
![]() $\mathrm {v\!+\!g}$
-open subsets that are weakly
$\mathrm {v\!+\!g}$
-open subsets that are weakly
![]() $\mathrm {v\!+\!g}$
-normal. When we pass to
$\mathrm {v\!+\!g}$
-normal. When we pass to
![]() $\widehat {X}$
equipped with the
$\widehat {X}$
equipped with the
![]() $\widehat {\mathrm {v\!+\!g}}$
-site, this gives the required conditions to apply the tools of Section 3.
$\widehat {\mathrm {v\!+\!g}}$
-site, this gives the required conditions to apply the tools of Section 3.
Section 6 is devoted to showing the Eilenberg-Steinrod axioms, finiteness, invariance and vanishing results for the associated sheaf cohomologies in the algebraic and
![]() ${\mathbf {\Gamma }_{\infty } }$
cases. The main difficulty concerns the homotopy axiom that, as usual, is proved using the Vietoris-Begle theorem. However, extra work is needed to verify the assumptions of the version of this theorem presented in Section 3. The results concerning finiteness and invariance in
${\mathbf {\Gamma }_{\infty } }$
cases. The main difficulty concerns the homotopy axiom that, as usual, is proved using the Vietoris-Begle theorem. However, extra work is needed to verify the assumptions of the version of this theorem presented in Section 3. The results concerning finiteness and invariance in
![]() ${\mathbf {\Gamma }_{\infty } }$
are obtained by adapting the methods used in [Reference Berarducci and Fornasiero7] and [Reference Edmundo and Prelli26]. After verifying that the strong deformation retraction given by the main theorem of [Reference Hrushovski and Loeser35] is a morphism of
${\mathbf {\Gamma }_{\infty } }$
are obtained by adapting the methods used in [Reference Berarducci and Fornasiero7] and [Reference Edmundo and Prelli26]. After verifying that the strong deformation retraction given by the main theorem of [Reference Hrushovski and Loeser35] is a morphism of
![]() $\widehat {\mathrm {v\!+\!g}}$
-sites, we obtain finiteness and invariance for stable completions in the quasi-projective case. The general case is then obtained using Mayer-Vietoris sequences based on the tools of Section 3.
$\widehat {\mathrm {v\!+\!g}}$
-sites, we obtain finiteness and invariance for stable completions in the quasi-projective case. The general case is then obtained using Mayer-Vietoris sequences based on the tools of Section 3.
Finally, Sections 7 and 8 gather the above-mentioned applications: the former is devoted to the relation with Berkovich spaces and the latter to the tameness results on cohomological complexity in families.
3
 ${\mathcal {T}}$
-spaces and
${\mathcal {T}}$
-spaces and
 ${\mathcal {T}}$
-sheaves
${\mathcal {T}}$
-sheaves
In this section, we will recall the notions of
![]() ${\mathcal {T}}$
-space and
${\mathcal {T}}$
-space and
![]() ${\mathcal {T}}$
-sheaves as well as some of the basic results obtained in [Reference Edmundo and Prelli27]. We then extend the theory of
${\mathcal {T}}$
-sheaves as well as some of the basic results obtained in [Reference Edmundo and Prelli27]. We then extend the theory of
![]() ${\mathcal {T}}$
-sheaves by introducing the notion of families of
${\mathcal {T}}$
-sheaves by introducing the notion of families of
![]() ${\mathcal {T}}$
-normal supports and proving several results in this context, generalising those already known in the o-minimal or locally semi-algebraic cases.
${\mathcal {T}}$
-normal supports and proving several results in this context, generalising those already known in the o-minimal or locally semi-algebraic cases.
Notations 3.1. Below, we let A be a commutative ring with unit. If X is a topological space (not necessarily Hausdorff), we denote by
![]() $\mathrm {Op}(X)$
the category whose objects are the open subsets of X, and the morphisms are the inclusions. We write
$\mathrm {Op}(X)$
the category whose objects are the open subsets of X, and the morphisms are the inclusions. We write
![]() $A_X$
for the constant sheaf on X with value A, and we let
$A_X$
for the constant sheaf on X with value A, and we let
![]() $\mathrm {Mod}(A_X)$
be the category of sheaves of
$\mathrm {Mod}(A_X)$
be the category of sheaves of
![]() $A_X$
-modules on X. The category
$A_X$
-modules on X. The category
![]() $\mathrm {Mod}(A_X)$
is a Grothendieck category: it admits enough injective objects, it admits a family of generators, filtrant inductive limits are exact, and we have on it the classical operations
$\mathrm {Mod}(A_X)$
is a Grothendieck category: it admits enough injective objects, it admits a family of generators, filtrant inductive limits are exact, and we have on it the classical operations
where
![]() $Z\subseteq X$
is a locally closed subset.
$Z\subseteq X$
is a locally closed subset.
Also recall that if
![]() $Z\subseteq X$
is a locally closed subset and
$Z\subseteq X$
is a locally closed subset and
![]() $i\colon Z\to X$
is the inclusion, then we have the operation
$i\colon Z\to X$
is the inclusion, then we have the operation
of extension by zero such that for
![]() ${\mathcal {F}}\in \mathrm {Mod}(A_Z)$
,
${\mathcal {F}}\in \mathrm {Mod}(A_Z)$
,
![]() $i_{!}{\mathcal {F}}$
is the unique sheaf in
$i_{!}{\mathcal {F}}$
is the unique sheaf in
![]() $\mathrm {Mod}(A_X)$
inducing
$\mathrm {Mod}(A_X)$
inducing
![]() ${\mathcal {F}}$
on Z and zero on
${\mathcal {F}}$
on Z and zero on
![]() $X\setminus Z$
. If
$X\setminus Z$
. If
![]() ${\mathcal {G}}\in \mathrm {Mod}(A_X),$
then
${\mathcal {G}}\in \mathrm {Mod}(A_X),$
then
If
![]() $f\colon X \to Y$
is a continuous map, Z is a locally closed subset of Y, and
$f\colon X \to Y$
is a continuous map, Z is a locally closed subset of Y, and

is a commutative diagram and
![]() ${\mathcal {F}}\in \mathrm {Mod} (A_{Z}),$
then
${\mathcal {F}}\in \mathrm {Mod} (A_{Z}),$
then
Below, we use these operations freely and refer the reader to [Reference Kashiwara and Schapira39, Chapter II, Sections 2.1–2.4] or [Reference Bredon14, Chapter I, Sections 1–6] (but the notation is different) for details about sheaves on topological spaces and the properties of these basic operations.
3.1
 ${\mathcal {T}}$
-sheaves
${\mathcal {T}}$
-sheaves
Here, we recall the definition of
![]() ${\mathcal {T}}$
-space given in [Reference Edmundo and Prelli27], adapting the construction of Kashiwara and Schapira [Reference Kashiwara and Schapira40], and we recall some of the results obtained in that paper for the category of sheaves on
${\mathcal {T}}$
-space given in [Reference Edmundo and Prelli27], adapting the construction of Kashiwara and Schapira [Reference Kashiwara and Schapira40], and we recall some of the results obtained in that paper for the category of sheaves on
![]() $X_{{\mathcal {T}}}$
. Those results generalise results from the case of sub-analytic sheaves, semi-algebraic sheaves or o-minimal sheaves. See Examples 3.7 below.
$X_{{\mathcal {T}}}$
. Those results generalise results from the case of sub-analytic sheaves, semi-algebraic sheaves or o-minimal sheaves. See Examples 3.7 below.
Definition 3.2. Let X be a topological space, and let
![]() ${\mathcal {T}} \subseteq \mathrm {Op}(X)$
be a family of open subsets of X such that
${\mathcal {T}} \subseteq \mathrm {Op}(X)$
be a family of open subsets of X such that
-
(i)
 ${\mathcal {T}}$
is a basis for the topology of X, and
${\mathcal {T}}$
is a basis for the topology of X, and
 $\varnothing \in {\mathcal {T}}$
.
$\varnothing \in {\mathcal {T}}$
. -
(ii)
 ${\mathcal {T}}$
is closed under finite unions and intersections.
${\mathcal {T}}$
is closed under finite unions and intersections.
Then we say that
-
• A
 ${\mathcal {T}}$
-subset is a finite Boolean combination of elements of
${\mathcal {T}}$
-subset is a finite Boolean combination of elements of
 ${\mathcal {T}}$
.
${\mathcal {T}}$
. -
• A closed (respectively, open)
 ${\mathcal {T}}$
-subset is a
${\mathcal {T}}$
-subset is a
 ${\mathcal {T}}$
-subset that is closed (respectively, open) in X.
${\mathcal {T}}$
-subset that is closed (respectively, open) in X. -
• A
 ${\mathcal {T}}$
-connected subset is a
${\mathcal {T}}$
-connected subset is a
 ${\mathcal {T}}$
-subset that is not the disjoint union of two proper clopen
${\mathcal {T}}$
-subset that is not the disjoint union of two proper clopen
 ${\mathcal {T}}$
-subsets (in the induced topology).
${\mathcal {T}}$
-subsets (in the induced topology).
If in addition
![]() ${\mathcal {T}}$
satisfies
${\mathcal {T}}$
satisfies
-
(iii) every
 $U \in {\mathcal {T}}$
has finitely many
$U \in {\mathcal {T}}$
has finitely many
 ${\mathcal {T}}$
-connected components that are in
${\mathcal {T}}$
-connected components that are in
 ${\mathcal {T}}$
,
${\mathcal {T}}$
,
then we say that X is a
![]() ${\mathcal {T}}$
-space.
${\mathcal {T}}$
-space.
Let X and
![]() ${\mathcal {T}}\subseteq \mathrm {Op} (X)$
satisfying (i) and (ii) of Definition 3.2. One can endow the category
${\mathcal {T}}\subseteq \mathrm {Op} (X)$
satisfying (i) and (ii) of Definition 3.2. One can endow the category
![]() ${\mathcal {T}}$
with a Grothendieck topology, called the
${\mathcal {T}}$
with a Grothendieck topology, called the
![]() ${\mathcal {T}}$
-topology, in the following way: a family
${\mathcal {T}}$
-topology, in the following way: a family
![]() $\{U_i\}_i$
in
$\{U_i\}_i$
in
![]() ${\mathcal {T}}$
is a covering of
${\mathcal {T}}$
is a covering of
![]() $U \in {\mathcal {T}}$
if it admits a finite subcover. We denote by
$U \in {\mathcal {T}}$
if it admits a finite subcover. We denote by
![]() $X_{{\mathcal {T}}}$
the associated site. For short, we write
$X_{{\mathcal {T}}}$
the associated site. For short, we write
![]() $A_{{\mathcal {T}}}$
instead of
$A_{{\mathcal {T}}}$
instead of
![]() $A_{X_{{\mathcal {T}}}}$
for the constant sheaf on
$A_{X_{{\mathcal {T}}}}$
for the constant sheaf on
![]() $X_{{\mathcal {T}}}$
with value A, and we let
$X_{{\mathcal {T}}}$
with value A, and we let
![]() $\mathrm {Mod}(A_{{\mathcal {T}}})$
be the category of sheaves of
$\mathrm {Mod}(A_{{\mathcal {T}}})$
be the category of sheaves of
![]() $A_{{\mathcal {T}}}$
-modules on
$A_{{\mathcal {T}}}$
-modules on
![]() $X_{{\mathcal {T}}}$
. If
$X_{{\mathcal {T}}}$
. If
![]() $\rho \colon X \to X_{{\mathcal {T}}}$
is the natural morphism of sites, then we have functors
$\rho \colon X \to X_{{\mathcal {T}}}$
is the natural morphism of sites, then we have functors
with
![]() $\rho ^{-1} \circ \rho _{*} \simeq {\mathrm {id}}$
(equivalently, the functor
$\rho ^{-1} \circ \rho _{*} \simeq {\mathrm {id}}$
(equivalently, the functor
![]() $\rho _*$
is fully faithful). See [Reference Edmundo and Prelli27, Proposition 2.1.6].
$\rho _*$
is fully faithful). See [Reference Edmundo and Prelli27, Proposition 2.1.6].
By [Reference Edmundo and Prelli27, Propositions 2.1.7 and 2.1.8], we have:
Fact 3.3.
-
(1) Let
 $\{{\mathcal {F}}_i\}_{i \in I}$
be a filtrant inductive system in
$\{{\mathcal {F}}_i\}_{i \in I}$
be a filtrant inductive system in
 $\mathrm {Mod}(A_{{\mathcal {T}}})$
, and let
$\mathrm {Mod}(A_{{\mathcal {T}}})$
, and let
 $U \in {\mathcal {T}}$
. Then
$U \in {\mathcal {T}}$
. Then  $$\begin{align*}\underset{i}{\underrightarrow{\lim}}\Gamma(U;{\mathcal{F}}_i) \stackrel{\sim}{\to} \Gamma(U;\underset{i}{\underrightarrow{\lim}} {\mathcal{F}}_i). \end{align*}$$
$$\begin{align*}\underset{i}{\underrightarrow{\lim}}\Gamma(U;{\mathcal{F}}_i) \stackrel{\sim}{\to} \Gamma(U;\underset{i}{\underrightarrow{\lim}} {\mathcal{F}}_i). \end{align*}$$
-
(2) Let
 ${\mathcal {F}}$
be a presheaf on
${\mathcal {F}}$
be a presheaf on
 $X_{{\mathcal {T}}}$
and assume that
$X_{{\mathcal {T}}}$
and assume that-
(i)
 ${\mathcal {F}}(\varnothing )=0,$
${\mathcal {F}}(\varnothing )=0,$
-
(ii) For any
 $U,V \in {\mathcal {T}}$
the sequence
$U,V \in {\mathcal {T}}$
the sequence
 $0 \to {{\mathcal {F}}(U\cup V)} \to {{\mathcal {F}}(U) \oplus {\mathcal {F}}(V)} \to {{\mathcal {F}}(U \cap V)}$
is exact.
$0 \to {{\mathcal {F}}(U\cup V)} \to {{\mathcal {F}}(U) \oplus {\mathcal {F}}(V)} \to {{\mathcal {F}}(U \cap V)}$
is exact.
Then
 ${\mathcal {F}} \in \mathrm {Mod}(A_{{\mathcal {T}}})$
.
${\mathcal {F}} \in \mathrm {Mod}(A_{{\mathcal {T}}})$
.
 $\Box $
$\Box $
-
Recall that any Boolean algebra
![]() ${\mathcal {A}}$
has an associated topological space that we denote by
${\mathcal {A}}$
has an associated topological space that we denote by
![]() $S({\mathcal {A}})$
, called its Stone space. The points in
$S({\mathcal {A}})$
, called its Stone space. The points in
![]() $S({\mathcal {A}})$
are the ultrafilters
$S({\mathcal {A}})$
are the ultrafilters
![]() $\alpha $
on
$\alpha $
on
![]() ${\mathcal {A}}$
. The topology on
${\mathcal {A}}$
. The topology on
![]() $S({\mathcal {A}})$
is generated by a basis of open and closed sets consisting of all sets of the form
$S({\mathcal {A}})$
is generated by a basis of open and closed sets consisting of all sets of the form
where
![]() $C\in {\mathcal {A}}$
. The space
$C\in {\mathcal {A}}$
. The space
![]() $S({\mathcal {A}})$
is a compactFootnote
1
totally disconnected space. Moreover, for each
$S({\mathcal {A}})$
is a compactFootnote
1
totally disconnected space. Moreover, for each
![]() $C \in {\mathcal {A}}$
, the subspace
$C \in {\mathcal {A}}$
, the subspace
![]() $\widetilde {C}$
is compact. See [Reference Johnstone37] for an introduction to this subject.
$\widetilde {C}$
is compact. See [Reference Johnstone37] for an introduction to this subject.
Let X and
![]() ${\mathcal {T}}\subseteq \mathrm {Op} (X)$
satisfying (i) and (ii) of Definition 3.2. Then as in [Reference Edmundo and Prelli27], we let
${\mathcal {T}}\subseteq \mathrm {Op} (X)$
satisfying (i) and (ii) of Definition 3.2. Then as in [Reference Edmundo and Prelli27], we let
and we make the following definitions:
-
• A subset S of X is a
 ${\mathcal {T}}_{loc}$
-subset if and only if
${\mathcal {T}}_{loc}$
-subset if and only if
 $S\cap V$
is a
$S\cap V$
is a
 $ {\mathcal {T}}$
-subset for every
$ {\mathcal {T}}$
-subset for every
 $V\in {\mathcal {T}}$
.
$V\in {\mathcal {T}}$
. -
• A closed (respectively, open)
 ${\mathcal {T}}_{loc}$
-subset is a
${\mathcal {T}}_{loc}$
-subset is a
 ${\mathcal {T}}_{loc}$
-subset that is closed (respectively, open) in X.
${\mathcal {T}}_{loc}$
-subset that is closed (respectively, open) in X. -
• A
 ${\mathcal {T}}_{loc}$
-connected subset is a
${\mathcal {T}}_{loc}$
-connected subset is a
 ${\mathcal {T}}_{loc}$
-subset that is not the disjoint union of two proper clopen
${\mathcal {T}}_{loc}$
-subset that is not the disjoint union of two proper clopen
 ${\mathcal {T}}_{loc}$
-subsets (in the induced topology).
${\mathcal {T}}_{loc}$
-subsets (in the induced topology).
Clearly,
![]() $\varnothing , X \in {\mathcal {T}}_{loc}$
,
$\varnothing , X \in {\mathcal {T}}_{loc}$
,
![]() ${\mathcal {T}}\subseteq {\mathcal {T}}_{loc}$
and
${\mathcal {T}}\subseteq {\mathcal {T}}_{loc}$
and
![]() ${\mathcal {T}}_{loc}$
is closed under finite intersections. Moreover, if
${\mathcal {T}}_{loc}$
is closed under finite intersections. Moreover, if
![]() $\{S_i\}_i$
is a family of
$\{S_i\}_i$
is a family of
![]() ${\mathcal {T}}_{loc}$
-subsets such that
${\mathcal {T}}_{loc}$
-subsets such that
![]() $\{i:S_i\cap W\neq \emptyset \}$
is finite for every
$\{i:S_i\cap W\neq \emptyset \}$
is finite for every
![]() $W\in {\mathcal {T}}$
, then the union and intersection of the family
$W\in {\mathcal {T}}$
, then the union and intersection of the family
![]() $\{S_i\}_i$
are
$\{S_i\}_i$
are
![]() ${\mathcal {T}}_{loc}$
-subsets. The complement of a
${\mathcal {T}}_{loc}$
-subsets. The complement of a
![]() ${\mathcal {T}}_{loc}$
-subset is also a
${\mathcal {T}}_{loc}$
-subset is also a
![]() ${\mathcal {T}}_{loc}$
-subset. Therefore, the
${\mathcal {T}}_{loc}$
-subset. Therefore, the
![]() ${\mathcal {T}}_{loc}$
-subsets form a Boolean algebra.
${\mathcal {T}}_{loc}$
-subsets form a Boolean algebra.
Definition 3.4. Let X be a topological space with
![]() ${\mathcal {T}}\subseteq \mathrm {Op} (X)$
as above, and let
${\mathcal {T}}\subseteq \mathrm {Op} (X)$
as above, and let
![]() ${\mathcal {A}}$
be the Boolean algebra of
${\mathcal {A}}$
be the Boolean algebra of
![]() ${\mathcal {T}}_{loc}$
-subsets of X. The topological space
${\mathcal {T}}_{loc}$
-subsets of X. The topological space
![]() $\widetilde {X}_{{\mathcal {T}}}$
is the data consisting of
$\widetilde {X}_{{\mathcal {T}}}$
is the data consisting of
-
• The points
 $\alpha $
of
$\alpha $
of
 $S({\mathcal {A}})$
such that
$S({\mathcal {A}})$
such that
 $U \in \alpha $
for some
$U \in \alpha $
for some
 $U \in {\mathcal {T}}$
;
$U \in {\mathcal {T}}$
; -
• A basis for the topology is given by the family of subsets
 $\{\widetilde {U}:U\in {\mathcal {T}}\}$
.
$\{\widetilde {U}:U\in {\mathcal {T}}\}$
.
We call
![]() $\widetilde {X}_{{\mathcal {T}}}$
the
$\widetilde {X}_{{\mathcal {T}}}$
the
![]() ${\mathcal {T}}$
-spectrum of X.
${\mathcal {T}}$
-spectrum of X.
With this topology, for
![]() $U \in {\mathcal {T}}$
, the set
$U \in {\mathcal {T}}$
, the set
![]() $\widetilde {U}$
is quasi-compact in
$\widetilde {U}$
is quasi-compact in
![]() $\widetilde {X}_{{\mathcal {T}}}$
since it is quasi-compact in
$\widetilde {X}_{{\mathcal {T}}}$
since it is quasi-compact in
![]() $S({\mathcal {A}})$
. Hence:
$S({\mathcal {A}})$
. Hence:
Fact 3.5.
![]() $\widetilde {X}_{{\mathcal {T}}}$
has a basis of quasi-compact open subsets given by
$\widetilde {X}_{{\mathcal {T}}}$
has a basis of quasi-compact open subsets given by
![]() $\{\widetilde {U}:U\in {\mathcal {T}}\}$
closed under finite intersections. Moreover, if
$\{\widetilde {U}:U\in {\mathcal {T}}\}$
closed under finite intersections. Moreover, if
![]() $X\in {\mathcal {T}}$
, then
$X\in {\mathcal {T}}$
, then
![]() $\widetilde {X}_{{\mathcal {T}}}=\widetilde {X}$
is a spectral topological space.
$\widetilde {X}_{{\mathcal {T}}}=\widetilde {X}$
is a spectral topological space.
![]() $\Box $
$\Box $
Furthermore, by [Reference Edmundo and Prelli27, Proposition 2.6.3], we also have:
Fact 3.6. There is an equivalence of categories
□
Note that in the statement of [Reference Edmundo and Prelli27, Proposition 2.6.3], X is assumed to be a
![]() ${\mathcal {T}}$
-space, but this is not necessary: all that is used is Fact 3.5 and [Reference Edmundo and Prelli27, Corollary 1.2.11] for
${\mathcal {T}}$
-space, but this is not necessary: all that is used is Fact 3.5 and [Reference Edmundo and Prelli27, Corollary 1.2.11] for
![]() $\widetilde {V}$
with
$\widetilde {V}$
with
![]() $V\in {\mathcal {T}}$
.
$V\in {\mathcal {T}}$
.
We now recall the main known examples of
![]() ${\mathcal {T}}$
-spaces.
${\mathcal {T}}$
-spaces.
Examples 3.7.
-
(1) Let
 $R=(R,<, 0,1,+,\cdot )$
be a real closed field, X be a locally semi-algebraic space and
$R=(R,<, 0,1,+,\cdot )$
be a real closed field, X be a locally semi-algebraic space and
 ${\mathcal {T}}= \{U \in \mathrm {Op}(X): U \,\, \text {is semi-algebraic}\}$
. Then X is a
${\mathcal {T}}= \{U \in \mathrm {Op}(X): U \,\, \text {is semi-algebraic}\}$
. Then X is a
 ${\mathcal {T}}$
-space, the associated site
${\mathcal {T}}$
-space, the associated site
 $X_{{\mathcal {T}}}$
is the semi-algebraic site on X of [Reference Delfs17, Reference Delfs and Knebusch18] (the
$X_{{\mathcal {T}}}$
is the semi-algebraic site on X of [Reference Delfs17, Reference Delfs and Knebusch18] (the
 ${\mathcal {T}}$
-subsets of X are the semi-algebraic subsets of X (see [Reference Bochnak, Coste and Roy13]), and the
${\mathcal {T}}$
-subsets of X are the semi-algebraic subsets of X (see [Reference Bochnak, Coste and Roy13]), and the
 ${\mathcal {T}}_{loc}$
-subsets of X are the locally semi-algebraic subsets of X (see [Reference Delfs and Knebusch18])). When X is semi-algebraic, then:
${\mathcal {T}}_{loc}$
-subsets of X are the locally semi-algebraic subsets of X (see [Reference Delfs and Knebusch18])). When X is semi-algebraic, then:-
(i)
 $\widetilde {X}_{{\mathcal {T}}} =\widetilde {X}$
is the semi-algebraic spectrum of X from [Reference Coste and Roy15]. For example, if
$\widetilde {X}_{{\mathcal {T}}} =\widetilde {X}$
is the semi-algebraic spectrum of X from [Reference Coste and Roy15]. For example, if
 $V\subseteq R^n$
is an affine real algebraic variety over R, then
$V\subseteq R^n$
is an affine real algebraic variety over R, then
 $\widetilde {V}$
is homeomorphic to
$\widetilde {V}$
is homeomorphic to
 $\mathrm {Sper}\,R[V]$
, the real spectrum of the coordinate ring
$\mathrm {Sper}\,R[V]$
, the real spectrum of the coordinate ring
 $R[V]$
of V (see [Reference Bochnak, Coste and Roy13, Chapter 7, Section 7.2] or [Reference Delfs17, Chapter I, Example 1.1]).
$R[V]$
of V (see [Reference Bochnak, Coste and Roy13, Chapter 7, Section 7.2] or [Reference Delfs17, Chapter I, Example 1.1]). -
(ii) There is an equivalence of categories
 $\mathrm {Mod}(A_{{\mathcal {T}}}) \simeq \mathrm {Mod}(A_{\widetilde {X}})$
(see [Reference Delfs17, Chapter 1, Proposition 1.4]).
$\mathrm {Mod}(A_{{\mathcal {T}}}) \simeq \mathrm {Mod}(A_{\widetilde {X}})$
(see [Reference Delfs17, Chapter 1, Proposition 1.4]).
-
-
(2) Let X be a real analytic manifold, and consider
 ${\mathcal {T}}=\{U \in \mathrm {Op}(X): U\,\, $
is sub-analytic relatively compact
${\mathcal {T}}=\{U \in \mathrm {Op}(X): U\,\, $
is sub-analytic relatively compact
 $\}$
. Then X is a
$\}$
. Then X is a
 ${\mathcal {T}}$
-space, and the associated site
${\mathcal {T}}$
-space, and the associated site
 $X_{{\mathcal {T}}}$
is the sub-analytic site
$X_{{\mathcal {T}}}$
is the sub-analytic site
 $X_{\mathrm {sa}}$
of [Reference Kashiwara and Schapira40, Reference Prelli49]. In this case, the
$X_{\mathrm {sa}}$
of [Reference Kashiwara and Schapira40, Reference Prelli49]. In this case, the
 ${\mathcal {T}}_{loc}$
-subsets are the sub-analytic subsets of X.Another example in the sub-analytic context is the conic sub-analytic site ([Reference Prelli50]).
${\mathcal {T}}_{loc}$
-subsets are the sub-analytic subsets of X.Another example in the sub-analytic context is the conic sub-analytic site ([Reference Prelli50]). -
(3) Let
 ${\mathbf {\Gamma }}= ({\Gamma },<, \ldots )$
be an arbitrary o-minimal structure without end points, X a definable space and
${\mathbf {\Gamma }}= ({\Gamma },<, \ldots )$
be an arbitrary o-minimal structure without end points, X a definable space and
 ${\mathcal {T}}=\{U \in \mathrm {Op}(X): U\,\, \text {is definable}\}$
. For the notion of definable space, see [Reference van den Dries53, Chapter 10]. Then X is a
${\mathcal {T}}=\{U \in \mathrm {Op}(X): U\,\, \text {is definable}\}$
. For the notion of definable space, see [Reference van den Dries53, Chapter 10]. Then X is a
 ${\mathcal {T}}$
-space, and the associated site
${\mathcal {T}}$
-space, and the associated site
 $X_{{\mathcal {T}}}$
is the o-minimal site
$X_{{\mathcal {T}}}$
is the o-minimal site
 $X_{\mathrm {def}}$
of [Reference Edmundo, Jones and Peatfield22]. Also note that the
$X_{\mathrm {def}}$
of [Reference Edmundo, Jones and Peatfield22]. Also note that the
 ${\mathcal {T}}$
-subsets of X are exactly the definable subsets of X (see Remark 4.12). Therefore,
${\mathcal {T}}$
-subsets of X are exactly the definable subsets of X (see Remark 4.12). Therefore,
 $\widetilde {X}_{\mathrm {def}} =\widetilde {X}$
is the o-minimal spectrum of X from [Reference Pillay46, Reference Edmundo, Jones and Peatfield22] (i.e., the points are types over
$\widetilde {X}_{\mathrm {def}} =\widetilde {X}$
is the o-minimal spectrum of X from [Reference Pillay46, Reference Edmundo, Jones and Peatfield22] (i.e., the points are types over
 ${\Gamma }$
concentrated on X). Moreover, there is an equivalence of categories
${\Gamma }$
concentrated on X). Moreover, there is an equivalence of categories
 $\mathrm {Mod}(A_{X_{\mathrm {def}}}) \simeq \mathrm {Mod}(A_{\widetilde {X}})$
([Reference Edmundo, Jones and Peatfield22]).
$\mathrm {Mod}(A_{X_{\mathrm {def}}}) \simeq \mathrm {Mod}(A_{\widetilde {X}})$
([Reference Edmundo, Jones and Peatfield22]).
3.2
 ${\mathcal {T}}$
-normality and families of
${\mathcal {T}}$
-normality and families of
 ${\mathcal {T}}$
-supports
${\mathcal {T}}$
-supports
Let
![]() ${\mathfrak T}$
be the category whose objects are pairs
${\mathfrak T}$
be the category whose objects are pairs
![]() $(X,{\mathcal {T}})$
with X a topological space,
$(X,{\mathcal {T}})$
with X a topological space,
![]() ${\mathcal {T}} \subseteq \mathrm {Op} (X)$
is a family of open subsets of X satisfying conditions (i) and (ii) of Definition 3.2 and such that
${\mathcal {T}} \subseteq \mathrm {Op} (X)$
is a family of open subsets of X satisfying conditions (i) and (ii) of Definition 3.2 and such that
![]() $X\in {\mathcal {T}}$
, and morphisms
$X\in {\mathcal {T}}$
, and morphisms
![]() $f\colon (X, {\mathcal {T}})\to (Y, {\mathcal {T}}')$
are (continuous) maps
$f\colon (X, {\mathcal {T}})\to (Y, {\mathcal {T}}')$
are (continuous) maps
![]() $f\colon X\to Y$
such that
$f\colon X\to Y$
such that
![]() $f^{-1}({\mathcal {T}}')\subseteq {\mathcal {T}}$
.
$f^{-1}({\mathcal {T}}')\subseteq {\mathcal {T}}$
.
Note that a morphism
![]() $f\colon (X,{\mathcal {T}})\to (Y,{\mathcal {T}}')$
of
$f\colon (X,{\mathcal {T}})\to (Y,{\mathcal {T}}')$
of
![]() ${\mathfrak T}$
defines a morphism of sites
${\mathfrak T}$
defines a morphism of sites
which extends to a homomorphism from the boolean algebra of
![]() ${\mathcal {T}}'$
-subsets of Y to the boolean algebra of
${\mathcal {T}}'$
-subsets of Y to the boolean algebra of
![]() ${\mathcal {T}}$
-subsets of X: namely,
${\mathcal {T}}$
-subsets of X: namely,
![]() $f^{-1}(C)$
is a
$f^{-1}(C)$
is a
![]() ${\mathcal {T}}$
-subset of X whenever C is a
${\mathcal {T}}$
-subset of X whenever C is a
![]() ${\mathcal {T}}'$
-subset of Y. It follows that we have an induced map
${\mathcal {T}}'$
-subset of Y. It follows that we have an induced map
between the corresponding spectral topological spaces, where
![]() $\widetilde {f}(\alpha )$
is the ultrafilter in
$\widetilde {f}(\alpha )$
is the ultrafilter in
![]() $\widetilde {Y}_{{\mathcal {T}}'}$
given by the collection
$\widetilde {Y}_{{\mathcal {T}}'}$
given by the collection
The map
![]() $\widetilde {f}\colon \widetilde {X}_{{\mathcal {T}}}\to \widetilde {Y}_{{\mathcal {T}}'}$
is continuous since if
$\widetilde {f}\colon \widetilde {X}_{{\mathcal {T}}}\to \widetilde {Y}_{{\mathcal {T}}'}$
is continuous since if
![]() $V\in {\mathcal {T}}',$
then clearly
$V\in {\mathcal {T}}',$
then clearly
![]() $\widetilde {f}^{-1}(\widetilde {V})=\widetilde {f^{-1}(V)}$
.
$\widetilde {f}^{-1}(\widetilde {V})=\widetilde {f^{-1}(V)}$
.
Later, we will also require the following generalisation of the above constructions:
Remark 3.8. Let
![]() $\zeta \colon X_{{\mathcal {T}}}\to Y_{{\mathcal {T}}'}$
be a morphism of sites that extends to a homomorphism from the boolean algebra of
$\zeta \colon X_{{\mathcal {T}}}\to Y_{{\mathcal {T}}'}$
be a morphism of sites that extends to a homomorphism from the boolean algebra of
![]() ${\mathcal {T}}'$
-subsets of Y to the boolean algebra of
${\mathcal {T}}'$
-subsets of Y to the boolean algebra of
![]() ${\mathcal {T}}$
-subsets of X. If
${\mathcal {T}}$
-subsets of X. If
![]() $\zeta (Y)=X$
and
$\zeta (Y)=X$
and
![]() $\zeta (A)\subseteq \zeta (B)$
whenever A and B are
$\zeta (A)\subseteq \zeta (B)$
whenever A and B are
![]() ${\mathcal {T}}'$
-subsets such that
${\mathcal {T}}'$
-subsets such that
![]() $A\subseteq B,$
then
$A\subseteq B,$
then
![]() $\zeta $
induces a continuous map
$\zeta $
induces a continuous map
![]() $\widetilde {\zeta }\colon \widetilde {X}_{{\mathcal {T}}}\to \widetilde {Y}_{{\mathcal {T}}'}$
, where
$\widetilde {\zeta }\colon \widetilde {X}_{{\mathcal {T}}}\to \widetilde {Y}_{{\mathcal {T}}'}$
, where
![]() $\widetilde {\zeta }(\alpha )$
is the ultrafilter of
$\widetilde {\zeta }(\alpha )$
is the ultrafilter of
![]() ${\mathcal {T}}'$
-subsets given by the collection
${\mathcal {T}}'$
-subsets given by the collection
If in addition
![]() $\zeta \colon X_{{\mathcal {T}}}\to Y_{{\mathcal {T}}'}$
is an isomorphism of sites, then
$\zeta \colon X_{{\mathcal {T}}}\to Y_{{\mathcal {T}}'}$
is an isomorphism of sites, then
![]() $\widetilde {\zeta }$
is a homeomorphism.
$\widetilde {\zeta }$
is a homeomorphism.
Also recall the following facts:
Remark 3.9 (Constructible subsets and topology).
Given
![]() $(X,{\mathcal {T}})$
an object of
$(X,{\mathcal {T}})$
an object of
![]() ${\mathfrak T},$
then
${\mathfrak T},$
then
![]() $\widetilde {X}$
equipped with the constructible topology is a compact totally disconnected space in which each constructible subset is clopen. Recall that by a constructible subset of
$\widetilde {X}$
equipped with the constructible topology is a compact totally disconnected space in which each constructible subset is clopen. Recall that by a constructible subset of
![]() $\widetilde {X}$
, we mean a subset of the form
$\widetilde {X}$
, we mean a subset of the form
![]() $\widetilde {Z}$
, where Z is a
$\widetilde {Z}$
, where Z is a
![]() ${\mathcal {T}}$
-subset of X, and the constructible topology on
${\mathcal {T}}$
-subset of X, and the constructible topology on
![]() $\widetilde {X}$
is the topology generated by the constructible subsets of
$\widetilde {X}$
is the topology generated by the constructible subsets of
![]() $\widetilde {X}$
.
$\widetilde {X}$
.
Let
![]() $\widetilde {{\mathfrak T}}$
be category with objects
$\widetilde {{\mathfrak T}}$
be category with objects
![]() $\widetilde {X}_{{\mathcal {T}}}$
for
$\widetilde {X}_{{\mathcal {T}}}$
for
![]() $(X,{\mathcal {T}})$
an object of
$(X,{\mathcal {T}})$
an object of
![]() ${\mathfrak T}$
and with morphisms
${\mathfrak T}$
and with morphisms
![]() $\widetilde {f}\colon \widetilde {X}_{{\mathcal {T}}}\to \widetilde {Y}_{{\mathcal {T}}'}$
for
$\widetilde {f}\colon \widetilde {X}_{{\mathcal {T}}}\to \widetilde {Y}_{{\mathcal {T}}'}$
for
![]() $f\colon (X,{\mathcal {T}})\to (Y,{\mathcal {T}}')$
a morphism of
$f\colon (X,{\mathcal {T}})\to (Y,{\mathcal {T}}')$
a morphism of
![]() ${\mathfrak T}$
. Below, we denote by
${\mathfrak T}$
. Below, we denote by
the functor sending an object
![]() $(X,{\mathcal {T}})$
of
$(X,{\mathcal {T}})$
of
![]() ${\mathfrak T}$
to
${\mathfrak T}$
to
![]() $\widetilde {X}_{{\mathcal {T}}}$
and sending a morphism
$\widetilde {X}_{{\mathcal {T}}}$
and sending a morphism
![]() $f\colon (X,{\mathcal {T}})\to (Y,{\mathcal {T}}')$
of
$f\colon (X,{\mathcal {T}})\to (Y,{\mathcal {T}}')$
of
![]() ${\mathfrak T}$
to
${\mathfrak T}$
to
![]() $\widetilde {f}\colon \widetilde {X}_{{\mathcal {T}}}\to \widetilde {Y}_{{\mathcal {T}}'}$
.
$\widetilde {f}\colon \widetilde {X}_{{\mathcal {T}}}\to \widetilde {Y}_{{\mathcal {T}}'}$
.
Remark 3.10. Let
![]() $(X, {\mathcal {T}})$
be an object of
$(X, {\mathcal {T}})$
be an object of
![]() ${\mathfrak T}$
. Then the restriction of the tilde functor
${\mathfrak T}$
. Then the restriction of the tilde functor
![]() ${\mathfrak T} \to \widetilde {{\mathfrak T}} $
induces an isomorphism between the boolean algebra of
${\mathfrak T} \to \widetilde {{\mathfrak T}} $
induces an isomorphism between the boolean algebra of
![]() ${\mathcal {T}}$
-subsets of X and the boolean algebra of constructible subsets of its
${\mathcal {T}}$
-subsets of X and the boolean algebra of constructible subsets of its
![]() ${\mathcal {T}}$
-spectrum
${\mathcal {T}}$
-spectrum
![]() $\widetilde {X}$
preserving open (respectively, closed), and X is
$\widetilde {X}$
preserving open (respectively, closed), and X is
![]() ${\mathcal {T}}$
-connected if and only if its
${\mathcal {T}}$
-connected if and only if its
![]() ${\mathcal {T}}$
-spectrum
${\mathcal {T}}$
-spectrum
![]() $\widetilde {X}$
is connected. Moreover, if
$\widetilde {X}$
is connected. Moreover, if
![]() $f\colon (X,{\mathcal {T}})\to (Y,{\mathcal {T}}')$
is a morphism of
$f\colon (X,{\mathcal {T}})\to (Y,{\mathcal {T}}')$
is a morphism of
![]() ${\mathfrak T}$
, then:
${\mathfrak T}$
, then:
-
• If C is a
 ${\mathcal {T}}'$
-subset of
${\mathcal {T}}'$
-subset of
 $Y,$
then
$Y,$
then
 $\widetilde {f^{-1}(C)}=\widetilde {f}^{-1}(\widetilde {C});$
$\widetilde {f^{-1}(C)}=\widetilde {f}^{-1}(\widetilde {C});$
-
• If
 $\beta \in \widetilde {Y}$
, then
$\beta \in \widetilde {Y}$
, then
 $\widetilde {f}^{-1}(\beta )$
is a quasi-compact subset of
$\widetilde {f}^{-1}(\beta )$
is a quasi-compact subset of
 $\widetilde {X}$
.
$\widetilde {X}$
.
For the latter, observe that
![]() $\widetilde {f}^{-1}(\beta )=\bigcap \{\widetilde {f^{-1}(C)}:C\in \beta \}$
, so it is compact in the constructible topology.
$\widetilde {f}^{-1}(\beta )=\bigcap \{\widetilde {f^{-1}(C)}:C\in \beta \}$
, so it is compact in the constructible topology.
The goal of this subsection is to extend to
![]() $({\mathfrak T}, \widetilde {{\mathfrak T}})$
some results from [Reference Edmundo, Jones and Peatfield22] and [Reference Edmundo and Prelli25] proved for the pair
$({\mathfrak T}, \widetilde {{\mathfrak T}})$
some results from [Reference Edmundo, Jones and Peatfield22] and [Reference Edmundo and Prelli25] proved for the pair
![]() $(\mathrm {Def}, \widetilde {\mathrm {Def}})$
, where
$(\mathrm {Def}, \widetilde {\mathrm {Def}})$
, where
![]() $\mathrm {Def}$
is the subcategory of
$\mathrm {Def}$
is the subcategory of
![]() ${\mathfrak T}$
of Example 3.7 (3): that is, it is the category of definable spaces in some fixed arbitrary o-minimal structure
${\mathfrak T}$
of Example 3.7 (3): that is, it is the category of definable spaces in some fixed arbitrary o-minimal structure
![]() ${\mathbf {\Gamma }} =({\Gamma }, <,\ldots )$
without end points, with morphisms being continuous definable maps between such definable spaces, and
${\mathbf {\Gamma }} =({\Gamma }, <,\ldots )$
without end points, with morphisms being continuous definable maps between such definable spaces, and
![]() $\widetilde {\mathrm {Def}}$
is the image of
$\widetilde {\mathrm {Def}}$
is the image of
![]() $\mathrm {Def}$
under
$\mathrm {Def}$
under
![]() ${\mathfrak T} \to \widetilde {{\mathfrak T}}$
.
${\mathfrak T} \to \widetilde {{\mathfrak T}}$
.
For
![]() $({\mathfrak T}, \widetilde {{\mathfrak T}}),$
just like in the case of
$({\mathfrak T}, \widetilde {{\mathfrak T}}),$
just like in the case of
![]() $(\mathrm {Def}, \widetilde {\mathrm {Def}}),$
normality will play the role that paracompactness plays in sheaf theory on topological spaces [Reference Bredon14, Chapter I, Section 6 and Chapter II, Sections 9–13] or the role that regular and paracompact plays in sheaf theory on locally semi-algebraic spaces [Reference Delfs17, Chapter II].
$(\mathrm {Def}, \widetilde {\mathrm {Def}}),$
normality will play the role that paracompactness plays in sheaf theory on topological spaces [Reference Bredon14, Chapter I, Section 6 and Chapter II, Sections 9–13] or the role that regular and paracompact plays in sheaf theory on locally semi-algebraic spaces [Reference Delfs17, Chapter II].
So we introduce and study a notion of normality adapted to
![]() ${\mathfrak T}:$
${\mathfrak T}:$
Definition 3.11. Let
![]() $(X, {\mathcal {T}})$
be an object of
$(X, {\mathcal {T}})$
be an object of
![]() ${\mathfrak T}$
. We say that X is
${\mathfrak T}$
. We say that X is
![]() ${\mathcal {T}}$
-normal if and only if one of the following equivalent conditions holds:
${\mathcal {T}}$
-normal if and only if one of the following equivalent conditions holds:
-
(1) For every disjoint, closed
 ${\mathcal {T}}$
-subsets C and D of X there are disjoint, open
${\mathcal {T}}$
-subsets C and D of X there are disjoint, open
 ${\mathcal {T}}$
-subsets U and V of X such that
${\mathcal {T}}$
-subsets U and V of X such that
 $C\subseteq U$
and
$C\subseteq U$
and
 $D\subseteq V$
.
$D\subseteq V$
. -
(2) For every
 $S\subseteq X$
closed
$S\subseteq X$
closed
 ${\mathcal {T}}$
-subset and
${\mathcal {T}}$
-subset and
 $U\subseteq X$
open
$U\subseteq X$
open
 ${\mathcal {T}}$
-subset such that
${\mathcal {T}}$
-subset such that
 $S\subseteq U$
, there are an open
$S\subseteq U$
, there are an open
 ${\mathcal {T}}$
-subset W of X and a closed
${\mathcal {T}}$
-subset W of X and a closed
 ${\mathcal {T}}$
-subset K of X such that
${\mathcal {T}}$
-subset K of X such that
 $S\subseteq W\subseteq K\subseteq U$
.
$S\subseteq W\subseteq K\subseteq U$
. -
(3) For every open
 ${\mathcal {T}}$
-subsets U and V of X such that
${\mathcal {T}}$
-subsets U and V of X such that
 $X=U\cup V$
there are closed
$X=U\cup V$
there are closed
 ${\mathcal {T}}$
-subsets
${\mathcal {T}}$
-subsets
 $A\subseteq U$
and
$A\subseteq U$
and
 $B\subseteq V$
of X such that
$B\subseteq V$
of X such that
 $X=A\cup B$
.
$X=A\cup B$
.
We let the reader convince her/himself of the equivalence of (1)–(3).
As in the case of
![]() $(\mathrm {Def}, \widetilde {\mathrm {Def}})$
([Reference Edmundo, Jones and Peatfield22, Theorem 2.13]), we have the following. Here we give a simpler proof.
$(\mathrm {Def}, \widetilde {\mathrm {Def}})$
([Reference Edmundo, Jones and Peatfield22, Theorem 2.13]), we have the following. Here we give a simpler proof.
Proposition 3.12. Let
![]() $(X,{\mathcal {T}})$
be an object of
$(X,{\mathcal {T}})$
be an object of
![]() ${\mathfrak T}$
. Then X is
${\mathfrak T}$
. Then X is
![]() ${\mathcal {T}}$
-normal if and only if its
${\mathcal {T}}$
-normal if and only if its
![]() ${\mathcal {T}}$
-spectrum
${\mathcal {T}}$
-spectrum
![]() $\widetilde {X}$
is a normal topological space.
$\widetilde {X}$
is a normal topological space.
Proof. By Remark 3.10 and quasi-compactness of
![]() $\widetilde {X}$
, it is immediate that if
$\widetilde {X}$
, it is immediate that if
![]() $\widetilde {X}$
is normal, then X is
$\widetilde {X}$
is normal, then X is
![]() ${\mathcal {T}}$
-normal. It is a standard fact that a spectral topological space is normal if and only if any two distinct closed points can be separated by disjoint open subsets (see [Reference Coste and Roy15, Proposition 2]). So let
${\mathcal {T}}$
-normal. It is a standard fact that a spectral topological space is normal if and only if any two distinct closed points can be separated by disjoint open subsets (see [Reference Coste and Roy15, Proposition 2]). So let
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
be two distinct closed points in
$\beta $
be two distinct closed points in
![]() $\widetilde {X}$
. Since
$\widetilde {X}$
. Since
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are closed points, we have
$\beta $
are closed points, we have
![]() $\{\alpha \}=\bigcap _{i\in I}C_i$
and
$\{\alpha \}=\bigcap _{i\in I}C_i$
and
![]() $\{\beta \}=\bigcap _{j\in J}D_j$
, where
$\{\beta \}=\bigcap _{j\in J}D_j$
, where
![]() $C_i$
s and
$C_i$
s and
![]() $D_j$
s are closed constructible subsets of
$D_j$
s are closed constructible subsets of
![]() $\widetilde {X}$
. Since
$\widetilde {X}$
. Since
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
are distinct, we have
$\beta $
are distinct, we have
By quasi-compactness of
![]() $\widetilde {X},$
there are
$\widetilde {X},$
there are
![]() $C=C_{i_1}\cap \ldots \cap C_{i_k}$
and
$C=C_{i_1}\cap \ldots \cap C_{i_k}$
and
![]() $D=D_{j_1}\cap \ldots \cap D_{j_l}$
such that
$D=D_{j_1}\cap \ldots \cap D_{j_l}$
such that
![]() $C\cap D=\emptyset $
. Since C and D are disjoint, closed constructible subsets of
$C\cap D=\emptyset $
. Since C and D are disjoint, closed constructible subsets of
![]() $\widetilde {X},$
by Remark 3.10, we can use the
$\widetilde {X},$
by Remark 3.10, we can use the
![]() ${\mathcal {T}}$
-normality of X to find disjoint, open constructible subsets of
${\mathcal {T}}$
-normality of X to find disjoint, open constructible subsets of
![]() $\widetilde {X}$
separating C and D and hence
$\widetilde {X}$
separating C and D and hence
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
.
$\beta $
.
As usual, normality implies the shrinking lemma, whose proof is standard; see, for example, [Reference Edmundo, Jones and Peatfield22, Proposition 2.17] or [Reference van den Dries53, Chapter 6, (3.6)]. In the
![]() ${\mathcal {T}}$
-spectra, due to the quasi-compactness of the base, we get a stronger result:
${\mathcal {T}}$
-spectra, due to the quasi-compactness of the base, we get a stronger result:
Corollary 3.13 (Shrinking lemma).
Suppose that
![]() $(X, {\mathcal {T}})$
is an object of
$(X, {\mathcal {T}})$
is an object of
![]() ${\mathfrak T}$
that is
${\mathfrak T}$
that is
![]() ${\mathcal {T}}$
-normal. If
${\mathcal {T}}$
-normal. If
![]() $\{U_i:i=1,\dots ,n\}$
is a covering of X (respectively, of
$\{U_i:i=1,\dots ,n\}$
is a covering of X (respectively, of
![]() $\widetilde {X}$
) by open
$\widetilde {X}$
) by open
![]() ${\mathcal {T}}$
-subsets of X (respectively, open subsets of
${\mathcal {T}}$
-subsets of X (respectively, open subsets of
![]() $\widetilde {X}$
), then there are open
$\widetilde {X}$
), then there are open
![]() ${\mathcal {T}}$
-subsets (respectively, open constructible subsets)
${\mathcal {T}}$
-subsets (respectively, open constructible subsets)
![]() $V_i$
and closed
$V_i$
and closed
![]() ${\mathcal {T}}$
-subsets (respectively, closed constructible subsets)
${\mathcal {T}}$
-subsets (respectively, closed constructible subsets)
![]() $K_i$
of X (respectively, of
$K_i$
of X (respectively, of
![]() $\widetilde {X}$
) (
$\widetilde {X}$
) (
![]() $1\leq i\leq n$
) with
$1\leq i\leq n$
) with
![]() $V_i\subseteq K_i\subseteq U_i$
and
$V_i\subseteq K_i\subseteq U_i$
and
![]() $X=\cup \{V_i:i=1,\dots , n\}$
(respectively,
$X=\cup \{V_i:i=1,\dots , n\}$
(respectively,
![]() $\widetilde {X}=\cup \{V_i:i=1,\dots , n\}$
).
$\widetilde {X}=\cup \{V_i:i=1,\dots , n\}$
).
![]() $\Box $
$\Box $
Later we will require the following weaker notion:
Definition 3.14. Let
![]() $(X, {\mathcal {T}})$
be an object of
$(X, {\mathcal {T}})$
be an object of
![]() ${\mathfrak T}$
. We say that X is weakly
${\mathfrak T}$
. We say that X is weakly
![]() ${\mathcal {T}}$
-normal if and only if one of the following equivalent conditions holds:
${\mathcal {T}}$
-normal if and only if one of the following equivalent conditions holds:
-
(1) For every disjoint,
 ${\mathcal {T}}$
-closed subsets C and D of X, there are disjoint,
${\mathcal {T}}$
-closed subsets C and D of X, there are disjoint,
 ${\mathcal {T}}$
-open subsets U and V of X such that
${\mathcal {T}}$
-open subsets U and V of X such that
 $C\subseteq U$
and
$C\subseteq U$
and
 $D\subseteq V$
.
$D\subseteq V$
. -
(2) For every
 $S\subseteq X \ {\mathcal {T}}$
-closed subset and
$S\subseteq X \ {\mathcal {T}}$
-closed subset and
 $U\subseteq X \ {\mathcal {T}}$
-open subset such that
$U\subseteq X \ {\mathcal {T}}$
-open subset such that
 $S\subseteq U$
, there are an
$S\subseteq U$
, there are an
 ${\mathcal {T}}$
-open subset W of X and a
${\mathcal {T}}$
-open subset W of X and a
 ${\mathcal {T}}$
-closed subset K of X such that
${\mathcal {T}}$
-closed subset K of X such that
 $S\subseteq W\subseteq K\subseteq U$
.
$S\subseteq W\subseteq K\subseteq U$
. -
(3) For every
 ${\mathcal {T}}$
-open subsets U and V of X such that
${\mathcal {T}}$
-open subsets U and V of X such that
 $X=U\cup V$
, there are
$X=U\cup V$
, there are
 ${\mathcal {T}}$
-closed subsets
${\mathcal {T}}$
-closed subsets
 $A\subseteq U$
and
$A\subseteq U$
and
 $B\subseteq V$
of X such that
$B\subseteq V$
of X such that
 $X=A\cup B$
.
$X=A\cup B$
.
We continue with the
![]() ${\mathfrak T}$
versions of some definitions from [Reference Edmundo and Prelli25] that are needed in the sequel.
${\mathfrak T}$
versions of some definitions from [Reference Edmundo and Prelli25] that are needed in the sequel.
Definition 3.15. Let
![]() $(X,{\mathcal {T}})$
be an object of
$(X,{\mathcal {T}})$
be an object of
![]() ${\mathfrak T}$
. A family of
${\mathfrak T}$
. A family of
![]() ${\mathcal {T}}$
-supports on
${\mathcal {T}}$
-supports on
![]() $(X,{\mathcal {T}})$
is a family of closed
$(X,{\mathcal {T}})$
is a family of closed
![]() ${\mathcal {T}}$
-subsets of X such that:
${\mathcal {T}}$
-subsets of X such that:
-
(1) Every closed
 ${\mathcal {T}}$
-subset contained in a member of
${\mathcal {T}}$
-subset contained in a member of
 $\Phi $
is in
$\Phi $
is in
 $\Phi $
.
$\Phi $
. -
(2)
 $\Phi $
is closed under finite unions.
$\Phi $
is closed under finite unions. $\Phi $
is said to be a family of
$\Phi $
is said to be a family of
 ${\mathcal {T}}$
-normal supports if, in addition,
${\mathcal {T}}$
-normal supports if, in addition, -
(3) Each element of
 $\Phi $
is
$\Phi $
is
 ${\mathcal {T}}$
-normal,
${\mathcal {T}}$
-normal, -
(4) For each element S of
 $\Phi $
, if
$\Phi $
, if
 $U\subseteq X$
is an open
$U\subseteq X$
is an open
 ${\mathcal {T}}$
-subset such that
${\mathcal {T}}$
-subset such that
 $S\subseteq U,$
then there are an open
$S\subseteq U,$
then there are an open
 ${\mathcal {T}}$
-subset W of X and a closed
${\mathcal {T}}$
-subset W of X and a closed
 ${\mathcal {T}}$
-subset K of X such that
${\mathcal {T}}$
-subset K of X such that
 $S\subseteq W\subseteq K\subseteq U$
and
$S\subseteq W\subseteq K\subseteq U$
and
 $K\in \Phi $
.
$K\in \Phi $
.
Example 3.16. Let
![]() $(X,{\mathcal {T}})$
be an object of
$(X,{\mathcal {T}})$
be an object of
![]() ${\mathfrak T}$
. Then the family of all closed
${\mathfrak T}$
. Then the family of all closed
![]() ${\mathcal {T}}$
-subsets of X is a family of
${\mathcal {T}}$
-subsets of X is a family of
![]() ${\mathcal {T}}$
-supports on
${\mathcal {T}}$
-supports on
![]() $(X,{\mathcal {T}})$
. Moreover, if X is
$(X,{\mathcal {T}})$
. Moreover, if X is
![]() ${\mathcal {T}}$
-normal, then this family is a family of
${\mathcal {T}}$
-normal, then this family is a family of
![]() ${\mathcal {T}}$
-normal supports on
${\mathcal {T}}$
-normal supports on
![]() $(X,{\mathcal {T}})$
. For other examples that play a crucial role in the paper, see Remarks 6.19 and 6.29.
$(X,{\mathcal {T}})$
. For other examples that play a crucial role in the paper, see Remarks 6.19 and 6.29.
Let
![]() $(X,{\mathcal {T}})$
be an object of
$(X,{\mathcal {T}})$
be an object of
![]() ${\mathfrak T}$
. If Z is a
${\mathfrak T}$
. If Z is a
![]() ${\mathcal {T}}$
-subset of X and
${\mathcal {T}}$
-subset of X and
![]() $\Phi $
is a family of
$\Phi $
is a family of
![]() ${\mathcal {T}}$
-supports on
${\mathcal {T}}$
-supports on
![]() $(X,{\mathcal {T}}),$
then we have families of
$(X,{\mathcal {T}}),$
then we have families of
![]() ${\mathcal {T}}\cap Z$
-supports
${\mathcal {T}}\cap Z$
-supports
and
on
![]() $(Z,{\mathcal {T}} \cap Z)$
.
$(Z,{\mathcal {T}} \cap Z)$
.
If
![]() $f\colon (X,{\mathcal {T}})\longrightarrow (Y,{\mathcal {T}}')$
is a morphism in
$f\colon (X,{\mathcal {T}})\longrightarrow (Y,{\mathcal {T}}')$
is a morphism in
![]() ${\mathfrak T}$
and
${\mathfrak T}$
and
![]() $\Psi $
is a family of
$\Psi $
is a family of
![]() ${\mathcal {T}}'$
-supports on
${\mathcal {T}}'$
-supports on
![]() $(Y,{\mathcal {T}}'),$
then we have a family of
$(Y,{\mathcal {T}}'),$
then we have a family of
![]() ${\mathcal {T}}$
-supports
${\mathcal {T}}$
-supports
on
![]() $(X,{\mathcal {T}})$
.
$(X,{\mathcal {T}})$
.
Remark 3.17 (Constructible family of supports).
Note that a family of
![]() ${\mathcal {T}}$
-supports
${\mathcal {T}}$
-supports
![]() $\Phi $
on an object
$\Phi $
on an object
![]() $(X,{\mathcal {T}})$
of
$(X,{\mathcal {T}})$
of
![]() ${\mathfrak T}$
determines a family of supports
${\mathfrak T}$
determines a family of supports
on the topological space
![]() $\widetilde {X}=\widetilde {X_{{\mathcal {T}}}}$
. By Remark 3.10, it follows that
$\widetilde {X}=\widetilde {X_{{\mathcal {T}}}}$
. By Remark 3.10, it follows that
We will say that the family of supports
![]() $\Psi $
on
$\Psi $
on
![]() $\widetilde {X}$
is a constructible family of supports on
$\widetilde {X}$
is a constructible family of supports on
![]() $\widetilde {X}$
if
$\widetilde {X}$
if
![]() $\Psi =\widetilde {\Phi }$
for some family of
$\Psi =\widetilde {\Phi }$
for some family of
![]() ${\mathcal {T}}$
-supports on
${\mathcal {T}}$
-supports on
![]() $(X,{\mathcal {T}})$
.
$(X,{\mathcal {T}})$
.
Remark 3.18 (Normal families of supports).
Let us call a family
![]() $\Psi $
of supports on a topological space Z a normal family of supports if:
$\Psi $
of supports on a topological space Z a normal family of supports if:
-
(1) Each element of
 $\Psi $
is normal.
$\Psi $
is normal. -
(2) Each element S of
 $\Psi $
has a fundamental system of normal (closed) neighbourhood in
$\Psi $
has a fundamental system of normal (closed) neighbourhood in
 $\Psi $
: that is, if
$\Psi $
: that is, if
 $U\subseteq Z$
is an open subset such that
$U\subseteq Z$
is an open subset such that
 $S\subseteq U,$
then there are an open subset W of Z and a closed subset K of Z such that
$S\subseteq U,$
then there are an open subset W of Z and a closed subset K of Z such that
 $S\subseteq W\subseteq K\subseteq U$
and
$S\subseteq W\subseteq K\subseteq U$
and
 $K\in \Psi $
.
$K\in \Psi $
.
We point out that instead of (2) above, just like for the notion of a paracompactifying family of supports in topology ([Reference Bredon14, Chapter I, Section 6 and Chapter II, Sections 9 - 13]) or the notion of a regular and paracompact family of supports in sheaf theory on locally semi-algebraic spaces ([Reference Delfs17, Chapter II]), we could have taken the following apparently weaker condition:
-
(2)* Each element S of
 $\Psi $
has a (closed) neighbourhood that is in
$\Psi $
has a (closed) neighbourhood that is in
 $\Psi $
: that is, there are an open subset W of Z and a closed subset K of Z such that
$\Psi $
: that is, there are an open subset W of Z and a closed subset K of Z such that
 $S\subseteq W\subseteq K$
and
$S\subseteq W\subseteq K$
and
 $K\in \Psi $
.
$K\in \Psi $
.
However, these conditions are equivalent. Assume (2)*. Let
![]() $S\in \Psi $
, and let
$S\in \Psi $
, and let
![]() $U\subseteq Z$
be an open subset such that
$U\subseteq Z$
be an open subset such that
![]() $S\subseteq U$
. Then there are an open subset
$S\subseteq U$
. Then there are an open subset
![]() $W'$
of Z and a closed subset
$W'$
of Z and a closed subset
![]() $K'$
of Z such that
$K'$
of Z such that
![]() $S\subseteq W'\subseteq K'$
and
$S\subseteq W'\subseteq K'$
and
![]() $K'\in \Psi $
. Then
$K'\in \Psi $
. Then
![]() $S\subseteq W'\cap U\subseteq K'$
, S is closed in
$S\subseteq W'\cap U\subseteq K'$
, S is closed in
![]() $K'$
and
$K'$
and
![]() $K'$
is normal by (1). Therefore, there are
$K'$
is normal by (1). Therefore, there are
![]() $W\subseteq K'$
an open subset in
$W\subseteq K'$
an open subset in
![]() $K'$
and
$K'$
and
![]() $K\subseteq K'$
a closed subset in
$K\subseteq K'$
a closed subset in
![]() $K'$
such that
$K'$
such that
![]() $S\subseteq W\subseteq K\subseteq W'\cap U$
. It follows that W is open in Z, K is closed in Z, and we get the stronger (2).
$S\subseteq W\subseteq K\subseteq W'\cap U$
. It follows that W is open in Z, K is closed in Z, and we get the stronger (2).
Also observe that as in the case of a paracompact family of supports ([Reference Bredon14, Chapter I, Section 6, Proposition 6.5]), if Y is a locally closed subset of Z and
![]() $\Psi $
is a normal family of supports on
$\Psi $
is a normal family of supports on
![]() $Z,$
then
$Z,$
then
![]() $\Psi _{|Y}$
is also a normal family of supports on Y. Indeed, Y is closed in an open U and
$\Psi _{|Y}$
is also a normal family of supports on Y. Indeed, Y is closed in an open U and
![]() $\Psi _{|Y}=(\Psi _{|U})_{|Y}=(\Psi _{|U})\cap Y$
.
$\Psi _{|Y}=(\Psi _{|U})_{|Y}=(\Psi _{|U})\cap Y$
.
By Proposition 3.12, it follows that:
Proposition 3.19. Let
![]() $(X,{\mathcal {T}})$
be an object of
$(X,{\mathcal {T}})$
be an object of
![]() ${\mathfrak T}$
and
${\mathfrak T}$
and
![]() $\Phi $
a family of
$\Phi $
a family of
![]() ${\mathcal {T}}$
-supports on
${\mathcal {T}}$
-supports on
![]() $(X,{\mathcal {T}})$
. Then
$(X,{\mathcal {T}})$
. Then
![]() $\Phi $
is
$\Phi $
is
![]() ${\mathcal {T}}$
-normal if and only if
${\mathcal {T}}$
-normal if and only if
![]() $\widetilde {\Phi }$
is normal.
$\widetilde {\Phi }$
is normal.
Moreover, if
![]() $\Phi $
is
$\Phi $
is
![]() ${\mathcal {T}}$
-normal, then the following holds:
${\mathcal {T}}$
-normal, then the following holds:
-
(*) Each element S of
 $\widetilde {\Phi }$
has a fundamental system of normal and constructible (closed) neighbourhoods in
$\widetilde {\Phi }$
has a fundamental system of normal and constructible (closed) neighbourhoods in
 $\widetilde {\Phi }$
: that is, if
$\widetilde {\Phi }$
: that is, if
 $U\subseteq \widetilde {X}$
is an open subset such that
$U\subseteq \widetilde {X}$
is an open subset such that
 $S\subseteq U,$
then there are an open constructible subset W of
$S\subseteq U,$
then there are an open constructible subset W of
 $\widetilde {X}$
and a closed constructible subset K of
$\widetilde {X}$
and a closed constructible subset K of
 $\widetilde {X}$
such that
$\widetilde {X}$
such that
 $S\subseteq W\subseteq K\subseteq U$
and
$S\subseteq W\subseteq K\subseteq U$
and
 $K\in \Psi $
.
$K\in \Psi $
.
Proof. Suppose that
![]() $\Phi $
is
$\Phi $
is
![]() ${\mathcal {T}}$
-normal. Let
${\mathcal {T}}$
-normal. Let
![]() $S\in \widetilde {\Phi }$
, and let
$S\in \widetilde {\Phi }$
, and let
![]() $U\subseteq \widetilde {X}$
be an open subset such that
$U\subseteq \widetilde {X}$
be an open subset such that
![]() $S\subseteq U$
. Since S is quasi-compact and U is a union of constructible open subsets of
$S\subseteq U$
. Since S is quasi-compact and U is a union of constructible open subsets of
![]() $\widetilde {X},$
there is an open constructible subset
$\widetilde {X},$
there is an open constructible subset
![]() $U'$
of
$U'$
of
![]() $\widetilde {X}$
such that
$\widetilde {X}$
such that
![]() $S\subseteq U'\subseteq U$
. Since
$S\subseteq U'\subseteq U$
. Since
![]() $S\in \widetilde {\Phi },$
there is
$S\in \widetilde {\Phi },$
there is
![]() $S'\in \widetilde {\Phi }$
constructible such that
$S'\in \widetilde {\Phi }$
constructible such that
![]() $S\subseteq S'$
. Hence
$S\subseteq S'$
. Hence
![]() $S=\bigcap \{S'\in \widetilde {\Phi }: S'\,\,\textrm {is constructible and}\,\,S\subseteq S'\}$
. Since
$S=\bigcap \{S'\in \widetilde {\Phi }: S'\,\,\textrm {is constructible and}\,\,S\subseteq S'\}$
. Since
![]() $(\widetilde {X}\setminus U')\cap S=\emptyset ,$
by quasi-compactness of
$(\widetilde {X}\setminus U')\cap S=\emptyset ,$
by quasi-compactness of
![]() $\widetilde {X}\setminus U'$
, there are
$\widetilde {X}\setminus U'$
, there are
![]() $S^{\prime }_1, \ldots , S^{\prime }_l\in \widetilde {\Phi },$
constructible with
$S^{\prime }_1, \ldots , S^{\prime }_l\in \widetilde {\Phi },$
constructible with
![]() $S\subseteq S_i'$
such that
$S\subseteq S_i'$
such that
![]() $(\bigcap _{i=1}^lS^{\prime }_i)\cap (\widetilde {X}\setminus U')=\emptyset $
. Let
$(\bigcap _{i=1}^lS^{\prime }_i)\cap (\widetilde {X}\setminus U')=\emptyset $
. Let
![]() $S'=\bigcap _{i=1}^lS^{\prime }_i$
. Then
$S'=\bigcap _{i=1}^lS^{\prime }_i$
. Then
![]() $S\subseteq S'\subseteq U'\subseteq U$
. Since
$S\subseteq S'\subseteq U'\subseteq U$
. Since
![]() $\Phi $
is
$\Phi $
is
![]() ${\mathcal {T}}$
-normal and
${\mathcal {T}}$
-normal and
![]() $S'$
and
$S'$
and
![]() $U'$
are constructible, there are an open constructible subset W of
$U'$
are constructible, there are an open constructible subset W of
![]() $\widetilde {X}$
and a closed constructible subset K of
$\widetilde {X}$
and a closed constructible subset K of
![]() $\widetilde {X}$
such that
$\widetilde {X}$
such that
![]() $S\subseteq S'\subseteq W\subseteq K\subseteq U'\subseteq U$
. This also shows
$S\subseteq S'\subseteq W\subseteq K\subseteq U'\subseteq U$
. This also shows
![]() $(\ast )$
.
$(\ast )$
.
Conversely, suppose
![]() $\widetilde {\Phi }$
is normal. If
$\widetilde {\Phi }$
is normal. If
![]() $S\in \widetilde {\Phi }$
is constructible and
$S\in \widetilde {\Phi }$
is constructible and
![]() $U\subseteq \widetilde {X}$
is an open constructible subset such that
$U\subseteq \widetilde {X}$
is an open constructible subset such that
![]() $S\subseteq U,$
then there are an open subset
$S\subseteq U,$
then there are an open subset
![]() $W'\subseteq \widetilde {X}$
and a closed subset
$W'\subseteq \widetilde {X}$
and a closed subset
![]() $K'\subseteq \widetilde {X}$
such that
$K'\subseteq \widetilde {X}$
such that
![]() $S\subseteq W'\subseteq K'\subseteq U$
. By quasi-compactness as above, there are an open constructible subset
$S\subseteq W'\subseteq K'\subseteq U$
. By quasi-compactness as above, there are an open constructible subset
![]() $W\subseteq \widetilde {X}$
and a closed constructible subset
$W\subseteq \widetilde {X}$
and a closed constructible subset
![]() $K\subseteq \widetilde {X}$
such that
$K\subseteq \widetilde {X}$
such that
![]() $S\subseteq W\subseteq W'\subseteq K'\subseteq K\subseteq U$
.
$S\subseteq W\subseteq W'\subseteq K'\subseteq K\subseteq U$
.
Below, we say that
![]() $\Psi $
is a family of normal and constructible supports on the spectral topological space
$\Psi $
is a family of normal and constructible supports on the spectral topological space
![]() $\widetilde {X}$
if
$\widetilde {X}$
if
![]() $\Psi =\widetilde {\Phi }$
for some family of
$\Psi =\widetilde {\Phi }$
for some family of
![]() ${\mathcal {T}}$
-normal supports on
${\mathcal {T}}$
-normal supports on
![]() $(X,{\mathcal {T}})$
.
$(X,{\mathcal {T}})$
.
3.3 Sheaf cohomology with
 ${\mathcal {T}}$
-supports
${\mathcal {T}}$
-supports
Let
![]() $(X,{\mathcal {T}})$
be an object of
$(X,{\mathcal {T}})$
be an object of
![]() ${\mathfrak T}$
. Due to the isomorphism
${\mathfrak T}$
. Due to the isomorphism
in analogy to what happened in the case
![]() $(\mathrm {Def}, \widetilde {\mathrm {Def}})$
([Reference Edmundo, Jones and Peatfield22] for o-minimal sheaf cohomology without supports and in [Reference Edmundo and Prelli25] in the presence of families of definable supports), in this subsection, we will develop sheaf cohomology on
$(\mathrm {Def}, \widetilde {\mathrm {Def}})$
([Reference Edmundo, Jones and Peatfield22] for o-minimal sheaf cohomology without supports and in [Reference Edmundo and Prelli25] in the presence of families of definable supports), in this subsection, we will develop sheaf cohomology on
![]() $X_{{\mathcal {T}}}$
via this tilde isomorphism.
$X_{{\mathcal {T}}}$
via this tilde isomorphism.
Definition 3.21. Let
![]() $(X,{\mathcal {T}})$
be an object of
$(X,{\mathcal {T}})$
be an object of
![]() ${\mathfrak T}$
,
${\mathfrak T}$
,
![]() $\Phi $
a family of
$\Phi $
a family of
![]() ${\mathcal {T}}$
-supports in
${\mathcal {T}}$
-supports in
![]() $(X,{\mathcal {T}})$
and
$(X,{\mathcal {T}})$
and
![]() ${\mathcal {F}} \in \mathrm {Mod} (A_{X_{{\mathcal {T}}}})$
. We define the
${\mathcal {F}} \in \mathrm {Mod} (A_{X_{{\mathcal {T}}}})$
. We define the
![]() ${\mathfrak T}$
-sheaf cohomology groups with
${\mathfrak T}$
-sheaf cohomology groups with
![]() ${\mathcal {T}}$
-supports in
${\mathcal {T}}$
-supports in
![]() $\Phi $
via the tilde isomorphism by
$\Phi $
via the tilde isomorphism by
where
![]() $\widetilde {{\mathcal {F}}}$
is the image of
$\widetilde {{\mathcal {F}}}$
is the image of
![]() ${\mathcal {F}}$
via the isomorphism
${\mathcal {F}}$
via the isomorphism
![]() $\mathrm {Mod} (A_{X_{{\mathcal {T}}}})\simeq \mathrm {Mod} (A_{\widetilde {X}})$
.
$\mathrm {Mod} (A_{X_{{\mathcal {T}}}})\simeq \mathrm {Mod} (A_{\widetilde {X}})$
.
If
![]() $f\colon (X,{\mathcal {T}})\longrightarrow (Y,{\mathcal {T}}')$
is a morphism in
$f\colon (X,{\mathcal {T}})\longrightarrow (Y,{\mathcal {T}}')$
is a morphism in
![]() ${\mathfrak T},$
we define the induced homomorphism
${\mathfrak T},$
we define the induced homomorphism
in cohomology to be the same as the homomorphism
in cohomology induced by the continuous map
![]() $\widetilde {f}\colon \widetilde {X}\longrightarrow \widetilde {Y}$
of topological spaces.
$\widetilde {f}\colon \widetilde {X}\longrightarrow \widetilde {Y}$
of topological spaces.
Below, we shall use a few facts about sheaf cohomology in topological spaces that can be found, for example, in [Reference Bredon14, Chapter II, Sections 1–8]. We will also need the following
![]() ${\mathfrak T}$
versions of [Reference Bredon14, Chapter II, 9.5] and [Reference Bredon14, Chapter II, 9.21], respectively.
${\mathfrak T}$
versions of [Reference Bredon14, Chapter II, 9.5] and [Reference Bredon14, Chapter II, 9.21], respectively.
Lemma 3.22. Let X be an object of
![]() $\widetilde {{\mathfrak T}}$
. Let Z be a subspace of X and Y a quasi-compact subset of Z having a fundamental system of normal and constructible locally closed neighbourhoods in X. Then for every
$\widetilde {{\mathfrak T}}$
. Let Z be a subspace of X and Y a quasi-compact subset of Z having a fundamental system of normal and constructible locally closed neighbourhoods in X. Then for every
![]() ${\mathcal {G}}\in {\mathrm {Mod}}(A_Z)$
, the canonical morphism
${\mathcal {G}}\in {\mathrm {Mod}}(A_Z)$
, the canonical morphism
where U ranges through the family of open constructible subsets of X containing Y, is an isomorphism.
Proof. Since Y is quasi-compact, the family of open neighbourhoods of Y in Z of the form
![]() $V\cap Z$
, where V is an open constructible subset of X, is a fundamental system of neighbourhoods of Y in Z. Hence, the morphism of the lemma is certainly injective.
$V\cap Z$
, where V is an open constructible subset of X, is a fundamental system of neighbourhoods of Y in Z. Hence, the morphism of the lemma is certainly injective.
To prove that it is surjective, consider a section
![]() $s\in \Gamma (Y;{\mathcal {G}} _{|Y})$
. There is a covering
$s\in \Gamma (Y;{\mathcal {G}} _{|Y})$
. There is a covering
![]() $\{U_j:j\in J\}$
of Y by open constructible subsets of X and sections
$\{U_j:j\in J\}$
of Y by open constructible subsets of X and sections
![]() $s_j\in \Gamma (U_j\cap Z; {\mathcal {G}}_{|U_j\cap Y})$
,
$s_j\in \Gamma (U_j\cap Z; {\mathcal {G}}_{|U_j\cap Y})$
,
![]() $j\in J$
, such that
$j\in J$
, such that
![]() $s_{j|U_j\cap Y}=s_{|U_j\cap Y}$
. Since Y is quasi-compact, we can assume that J is finite, so
$s_{j|U_j\cap Y}=s_{|U_j\cap Y}$
. Since Y is quasi-compact, we can assume that J is finite, so
![]() $\cup \{U_j:j\in J\}$
is an open constructible subset of X. Therefore, there are an open constructible subset
$\cup \{U_j:j\in J\}$
is an open constructible subset of X. Therefore, there are an open constructible subset
![]() $O'$
in X and a normal, constructible locally closed subset
$O'$
in X and a normal, constructible locally closed subset
![]() $X'$
in X such that
$X'$
in X such that
![]() $Y\subseteq O'\subseteq X'\subseteq \cup \{U_j:j\in J\}$
. For each
$Y\subseteq O'\subseteq X'\subseteq \cup \{U_j:j\in J\}$
. For each
![]() $j\in J$
, let
$j\in J$
, let
![]() $U^{\prime }_j=U_j\cap X'$
. Since
$U^{\prime }_j=U_j\cap X'$
. Since
![]() $X'$
is normal and constructible, by the shrinking lemma, there are open constructible subsets
$X'$
is normal and constructible, by the shrinking lemma, there are open constructible subsets
![]() $\{V^{\prime }_j:j\in J\}$
of
$\{V^{\prime }_j:j\in J\}$
of
![]() $X'$
and closed constructible subsets
$X'$
and closed constructible subsets
![]() $\{K^{\prime }_j:j\in J\}$
of
$\{K^{\prime }_j:j\in J\}$
of
![]() $X'$
such that
$X'$
such that
![]() $V^{\prime }_j\subseteq K^{\prime }_j\subseteq U^{\prime }_j$
for every
$V^{\prime }_j\subseteq K^{\prime }_j\subseteq U^{\prime }_j$
for every
![]() $j\in J$
and
$j\in J$
and
![]() $X'= \cup \{V^{\prime }_j:j\in J\}$
. Since
$X'= \cup \{V^{\prime }_j:j\in J\}$
. Since
![]() $X'$
is a constructible locally closed subset of
$X'$
is a constructible locally closed subset of
![]() $X,$
it is a constructible closed subset of an open subset of
$X,$
it is a constructible closed subset of an open subset of
![]() $X,$
which by quasi-compactness we may assume is also constructible. Replacing X by that constructible open subset, we may assume that
$X,$
which by quasi-compactness we may assume is also constructible. Replacing X by that constructible open subset, we may assume that
![]() $X'$
is a constructible closed subset of X. For each
$X'$
is a constructible closed subset of X. For each
![]() $j\in J$
, let
$j\in J$
, let
![]() $V_j=V^{\prime }_j\cap O'$
and
$V_j=V^{\prime }_j\cap O'$
and
![]() $K_j=K^{\prime }_j$
. Then for each
$K_j=K^{\prime }_j$
. Then for each
![]() $j\in J, \ V_j$
is an open constructible subset of X and
$j\in J, \ V_j$
is an open constructible subset of X and
![]() $K_j$
is a closed constructible subset of X with
$K_j$
is a closed constructible subset of X with
![]() $V_j\subseteq K_j\subseteq U_j$
and
$V_j\subseteq K_j\subseteq U_j$
and
![]() $Y\subseteq \cup \{V_j:j\in J\}$
.
$Y\subseteq \cup \{V_j:j\in J\}$
.
For
![]() $x \in Z\cap O'$
, set
$x \in Z\cap O'$
, set
![]() $J(x)=\{j\in J:x\in K_j\}$
, and let
$J(x)=\{j\in J:x\in K_j\}$
, and let
 $$\begin{align*}W_x = (\bigcap_{x \in V_l}V_l \cap \bigcap_{j\in J(x)}U_j) \setminus \bigcup_{k \notin J (x)}K_k. \end{align*}$$
$$\begin{align*}W_x = (\bigcap_{x \in V_l}V_l \cap \bigcap_{j\in J(x)}U_j) \setminus \bigcup_{k \notin J (x)}K_k. \end{align*}$$
Then
![]() $W_x$
is a constructible neighbourhood of x in X such that if
$W_x$
is a constructible neighbourhood of x in X such that if
![]() $y\in W_x$
, then
$y\in W_x$
, then
![]() $J(y)\subseteq J(x)$
. Indeed, suppose that
$J(y)\subseteq J(x)$
. Indeed, suppose that
![]() $y\in W_x$
, and let
$y\in W_x$
, and let
![]() $i\in J(y)$
. Then
$i\in J(y)$
. Then
![]() $y\in K_i$
and either
$y\in K_i$
and either
![]() $x\in K_i$
, in which case
$x\in K_i$
, in which case
![]() $i\in J(x)$
, or
$i\in J(x)$
, or
![]() $x\not \in K_i$
, in which case
$x\not \in K_i$
, in which case
![]() $i\not \in J(x)$
, so
$i\not \in J(x)$
, so
![]() $y\in W_x\cap K_i=\emptyset $
.
$y\in W_x\cap K_i=\emptyset $
.
Observe that for all
![]() $i,j \in J(x)$
, we have that
$i,j \in J(x)$
, we have that
![]() $W_x$
is an open subset of both
$W_x$
is an open subset of both
![]() $U_i$
and
$U_i$
and
![]() $U_j$
. Hence, for every
$U_j$
. Hence, for every
![]() $i,j \in J(x)$
, we have
$i,j \in J(x)$
, we have
![]() $s_{i|W_x\cap Y}= s_{|W_x\cap Y}=s_{j|W_x\cap Y}$
. So, for
$s_{i|W_x\cap Y}= s_{|W_x\cap Y}=s_{j|W_x\cap Y}$
. So, for
![]() $y \in W_x \cap Y$
, we have
$y \in W_x \cap Y$
, we have
![]() $(s_i)_y=(s_j)_y$
for any
$(s_i)_y=(s_j)_y$
for any
![]() $i,j \in J (x)$
. This implies that the set
$i,j \in J (x)$
. This implies that the set
 $$\begin{align*}W=\{z\in (\bigcup_{j\in J}V_j)\cap Z: (s_i)_z=(s_j)_z\,\,\textrm{for any}\,\, i,j\in J(z)\}\end{align*}$$
$$\begin{align*}W=\{z\in (\bigcup_{j\in J}V_j)\cap Z: (s_i)_z=(s_j)_z\,\,\textrm{for any}\,\, i,j\in J(z)\}\end{align*}$$
contains Y (clearly
![]() $Y\subseteq \bigcup _{x\in Z} W_x\cap Y\subseteq (\bigcup _{j\in J}V_j)\cap Z$
). On the other hand, if
$Y\subseteq \bigcup _{x\in Z} W_x\cap Y\subseteq (\bigcup _{j\in J}V_j)\cap Z$
). On the other hand, if
![]() $z\in W$
, then for any
$z\in W$
, then for any
![]() $i,j\in J(z)$
, we have
$i,j\in J(z)$
, we have
![]() $(s_i)_z=(s_j)_z$
, so
$(s_i)_z=(s_j)_z$
, so
![]() $s_i=s_j$
in an open neighbourhood of z. Since
$s_i=s_j$
in an open neighbourhood of z. Since
![]() $J(z)$
is finite, z has an open neighbourhood in Z on which
$J(z)$
is finite, z has an open neighbourhood in Z on which
![]() $s_i=s_j$
for any
$s_i=s_j$
for any
![]() $i,j \in J(z)$
. Thus W is an open neighbourhood of Y in Z. Since Y is quasi-compact, we may assume that W is of the form
$i,j \in J(z)$
. Thus W is an open neighbourhood of Y in Z. Since Y is quasi-compact, we may assume that W is of the form
![]() $U\cap Z$
for some open constructible subset U of X. Since
$U\cap Z$
for some open constructible subset U of X. Since
![]() $s_{i_{|W \cap V_i \cap V_j}} =s_{j_{|W \cap V_i \cap V_j}},$
there exists
$s_{i_{|W \cap V_i \cap V_j}} =s_{j_{|W \cap V_i \cap V_j}},$
there exists
![]() $t\in \Gamma (W;{\mathcal {G}} )$
such that
$t\in \Gamma (W;{\mathcal {G}} )$
such that
![]() $t_ {|W \cap V_j}=s_{j|W \cap V_j}$
. This proves that the morphism is surjective.
$t_ {|W \cap V_j}=s_{j|W \cap V_j}$
. This proves that the morphism is surjective.
A general form of Lemma 3.22 is:
Lemma 3.23. Assume that X is an object of
![]() $\widetilde {{\mathfrak T}}$
. Let Z be a subspace of X,
$\widetilde {{\mathfrak T}}$
. Let Z be a subspace of X,
![]() $\Phi $
a normal and constructible family of supports on X and Y a subset of Z such that for every constructible
$\Phi $
a normal and constructible family of supports on X and Y a subset of Z such that for every constructible
![]() $D\in \Phi ,$
,
$D\in \Phi ,$
,
![]() $D\cap Y$
is a quasi-compact subset of Z having a fundamental system of normal and constructible locally closed neighbourhoods in X. Then for every
$D\cap Y$
is a quasi-compact subset of Z having a fundamental system of normal and constructible locally closed neighbourhoods in X. Then for every
![]() ${\mathcal {G}} \in \mathrm {Mod} (A_Z)$
, the canonical morphism
${\mathcal {G}} \in \mathrm {Mod} (A_Z)$
, the canonical morphism
where U ranges through the family of open constructible subsets of X containing Y, is an isomorphism.
Proof. Let us prove injectivity. Let
![]() $s \in \Gamma _{D\cap U \cap Z}(U\cap Z;{\mathcal {G}})$
, with
$s \in \Gamma _{D\cap U \cap Z}(U\cap Z;{\mathcal {G}})$
, with
![]() $D \in \Phi $
and
$D \in \Phi $
and
![]() $U \supset Y$
open constructible subset of X and such that
$U \supset Y$
open constructible subset of X and such that
![]() $s_{|D \cap Y}=0$
. By quasi-compactness of
$s_{|D \cap Y}=0$
. By quasi-compactness of
![]() $D \cap Y$
, there exists an open constructible neighbourhood V of
$D \cap Y$
, there exists an open constructible neighbourhood V of
![]() $D\cap Y$
in X such that
$D\cap Y$
in X such that
![]() $s_{|V\cap D\cap Z}=0$
. Replacing V with its intersection with U if necessary, we may assume that
$s_{|V\cap D\cap Z}=0$
. Replacing V with its intersection with U if necessary, we may assume that
![]() $V \subseteq U$
. Set
$V \subseteq U$
. Set
![]() $W=V \cup (U \setminus D)$
. Then W is open constructible in X,
$W=V \cup (U \setminus D)$
. Then W is open constructible in X,
![]() $Y\subseteq W\subseteq U$
and
$Y\subseteq W\subseteq U$
and
![]() $s_{|W\cap Z}=0$
.
$s_{|W\cap Z}=0$
.
Let us prove that the morphism is surjective. Let
![]() $s\in \Gamma _{\Phi \cap Y}(Y;{\mathcal {G}}_{|Y})$
, and consider a closed, normal and constructible set
$s\in \Gamma _{\Phi \cap Y}(Y;{\mathcal {G}}_{|Y})$
, and consider a closed, normal and constructible set
![]() $C\in \Phi $
such that the support of s is contained in
$C\in \Phi $
such that the support of s is contained in
![]() $C\cap Y$
. Since
$C\cap Y$
. Since
![]() $\Phi $
is normal and constructible, there exist a closed, normal and constructible set
$\Phi $
is normal and constructible, there exist a closed, normal and constructible set
![]() $D\in \Phi $
and an open constructible set
$D\in \Phi $
and an open constructible set
![]() $O\subseteq X$
such that
$O\subseteq X$
such that
![]() $C\subseteq O\subseteq D$
. We shall find
$C\subseteq O\subseteq D$
. We shall find
![]() $\widetilde {t} \in \Gamma _D(U \cap Z;{\mathcal {G}})$
such that
$\widetilde {t} \in \Gamma _D(U \cap Z;{\mathcal {G}})$
such that
![]() $\widetilde {t}_{|Y}=s$
. After applying Lemma 3.22 above to X,
$\widetilde {t}_{|Y}=s$
. After applying Lemma 3.22 above to X,
![]() $D\cap Z$
and
$D\cap Z$
and
![]() $D \cap Y$
, we see that there exist an open, constructible neighbourhood V of
$D \cap Y$
, we see that there exist an open, constructible neighbourhood V of
![]() $D\cap Y$
in X and a section
$D\cap Y$
in X and a section
![]() $t\in \Gamma (V\cap D\cap Z;{\mathcal G})$
such that
$t\in \Gamma (V\cap D\cap Z;{\mathcal G})$
such that
![]() $t_{|D\cap Y}=s_{|D\cap Y}$
. Since
$t_{|D\cap Y}=s_{|D\cap Y}$
. Since
![]() $t_{|(D\setminus O)\cap Y}=0$
, then each point x of
$t_{|(D\setminus O)\cap Y}=0$
, then each point x of
![]() $(D\setminus O) \cap Y$
has an open constructible neighbourhood
$(D\setminus O) \cap Y$
has an open constructible neighbourhood
![]() $W_x \subseteq V$
such that
$W_x \subseteq V$
such that
![]() $t_{|W_x\cap D\cap Z}=0$
. Using quasi-compactness of
$t_{|W_x\cap D\cap Z}=0$
. Using quasi-compactness of
![]() $(D\setminus O)\cap Y$
(it is closed on the quasi-compact set
$(D\setminus O)\cap Y$
(it is closed on the quasi-compact set
![]() $D\cap Y$
), there exists a finite number of points
$D\cap Y$
), there exists a finite number of points
![]() $x_1,\ldots ,x_n$
such that
$x_1,\ldots ,x_n$
such that
![]() $(D\setminus O) \cap Y \subseteq \bigcup _{i=1}^nW_{x_i}$
. Then
$(D\setminus O) \cap Y \subseteq \bigcup _{i=1}^nW_{x_i}$
. Then
![]() $W:= \bigcup _{i=1}^nW_{x_i}$
is an open constructible subset and
$W:= \bigcup _{i=1}^nW_{x_i}$
is an open constructible subset and
![]() $t_{|W\cap D \cap Z}=0$
. Let
$t_{|W\cap D \cap Z}=0$
. Let
![]() $U_1=(V\cap O)\cup W$
. Then
$U_1=(V\cap O)\cup W$
. Then
![]() $U_1$
is open constructible, and
$U_1$
is open constructible, and
![]() $D\cap Y\subseteq U_1\subseteq V$
. Define
$D\cap Y\subseteq U_1\subseteq V$
. Define
![]() $t' \in \Gamma (U_1\cap Z; {\mathcal G})$
by:
$t' \in \Gamma (U_1\cap Z; {\mathcal G})$
by:
![]() $t^{\prime }_{|V\cap O\cap Z}=t_{|V\cap O\cap Z}$
and
$t^{\prime }_{|V\cap O\cap Z}=t_{|V\cap O\cap Z}$
and
![]() $t^{\prime }_{|W\cap Z}=0$
. This is well defined since
$t^{\prime }_{|W\cap Z}=0$
. This is well defined since
![]() $(V\cap O\cap Z)\cap (W\cap Z)\subseteq W\cap D \cap Z$
and
$(V\cap O\cap Z)\cap (W\cap Z)\subseteq W\cap D \cap Z$
and
![]() $t_{|W\cap D \cap Z}=0$
. Also observe that
$t_{|W\cap D \cap Z}=0$
. Also observe that
![]() $t^{\prime }_{|U_1\cap D\cap Z}=t$
. Let
$t^{\prime }_{|U_1\cap D\cap Z}=t$
. Let
![]() $U_2=X\setminus D$
. Then
$U_2=X\setminus D$
. Then
![]() $U=U_1\cup U_2$
is open constructible,
$U=U_1\cup U_2$
is open constructible,
![]() $Y\subseteq U$
,
$Y\subseteq U$
,
![]() $U_1\cap U_2\subseteq W$
, and we can define
$U_1\cap U_2\subseteq W$
, and we can define
![]() $\widetilde {t} \in \Gamma (U\cap Z;\mathcal {G})$
in the following way:
$\widetilde {t} \in \Gamma (U\cap Z;\mathcal {G})$
in the following way:
![]() $\widetilde {t}_{|U_1\cap Z}=t^{\prime }_{|U_1\cap Z}$
,
$\widetilde {t}_{|U_1\cap Z}=t^{\prime }_{|U_1\cap Z}$
,
![]() $\widetilde {t}_{|U_2\cap Z}=0$
. It is well defined since
$\widetilde {t}_{|U_2\cap Z}=0$
. It is well defined since
![]() $U_1 \cap U_2 \subseteq W$
and
$U_1 \cap U_2 \subseteq W$
and
![]() $t^{\prime }_{|W\cap Z}=0$
. Moreover
$t^{\prime }_{|W\cap Z}=0$
. Moreover
![]() $\mathrm {supp}\,\widetilde {t} \subseteq D$
and
$\mathrm {supp}\,\widetilde {t} \subseteq D$
and
![]() $\widetilde {t}_{|Y}=s$
as required.
$\widetilde {t}_{|Y}=s$
as required.
For the locally semi-algebraic analogues of Lemmas 3.22 and 3.23, see [Reference Delfs17, Chapter II, Lemma 3.1 and Proposition 3.2]. Note that in the locally semi-algebraic case, one only requires that Y has a paracompact and regular locally semi-algebraic neighbourhood in
![]() $X,$
instead of a fundamental system of such neighbourhoods, since under this assumption, the family of all open locally semi-algebraic neighbourhoods of Y in X is a fundamental system of neighbourhoods of Y in X ([Reference Delfs17, Chapter I, Lemma 5.5]). Moreover, these are paracompact and regular: that is, they are normal, and one can apply the shrinking lemma ([Reference Delfs17, Chapter I, Proposition 5.1]). The assumption for
$X,$
instead of a fundamental system of such neighbourhoods, since under this assumption, the family of all open locally semi-algebraic neighbourhoods of Y in X is a fundamental system of neighbourhoods of Y in X ([Reference Delfs17, Chapter I, Lemma 5.5]). Moreover, these are paracompact and regular: that is, they are normal, and one can apply the shrinking lemma ([Reference Delfs17, Chapter I, Proposition 5.1]). The assumption for
![]() $\Phi $
implies that the same holds for each
$\Phi $
implies that the same holds for each
![]() $D\cap Y$
.
$D\cap Y$
.
The o-minimal versions are [Reference Edmundo and Prelli25, Lemmas 3.2 and 3.3]. Unfortunately, in the statement of these lemmas and also in [Reference Edmundo and Prelli25, Proposition 3.7], the assumption that Y (respectively,
![]() $D\cap Y$
) has a fundamental system of normal and constructible locally closed neighbourhoods in X is missing. However, note that this does not affect the main results of that paper since in those results,
$D\cap Y$
) has a fundamental system of normal and constructible locally closed neighbourhoods in X is missing. However, note that this does not affect the main results of that paper since in those results,
![]() $Y=X$
and each D satisfies the hypothesis as
$Y=X$
and each D satisfies the hypothesis as
![]() $\Phi $
is normal and constructible. The only results affected are the Vietoris-Begle theorem and the homotopy axiom ([Reference Edmundo and Prelli25, Theorems 2.13 and 2.14]) that we fix below.
$\Phi $
is normal and constructible. The only results affected are the Vietoris-Begle theorem and the homotopy axiom ([Reference Edmundo and Prelli25, Theorems 2.13 and 2.14]) that we fix below.
Recall that a sheaf
![]() ${\mathcal {F}}$
on a topological space X with a family of supports
${\mathcal {F}}$
on a topological space X with a family of supports
![]() $\Phi $
is
$\Phi $
is
![]() $\Phi $
-soft if and only if the restriction
$\Phi $
-soft if and only if the restriction
![]() $\Gamma (X;{\mathcal {F}})\longrightarrow \Gamma (S;{\mathcal {F}}_{|S})$
is surjective for every
$\Gamma (X;{\mathcal {F}})\longrightarrow \Gamma (S;{\mathcal {F}}_{|S})$
is surjective for every
![]() $S\in \Phi $
. If
$S\in \Phi $
. If
![]() $\Phi $
consists of all closed subsets of X, then
$\Phi $
consists of all closed subsets of X, then
![]() ${\mathcal {F}}$
is simply called soft.
${\mathcal {F}}$
is simply called soft.
The topological analogue of the next result is [Reference Bredon14, Chapter II, 9.3].
Proposition 3.24. Let X be a topological space and
![]() ${\mathcal {F}}$
be a sheaf in
${\mathcal {F}}$
be a sheaf in
![]() $\mathrm {Mod} (A_X)$
. Suppose that
$\mathrm {Mod} (A_X)$
. Suppose that
![]() $\Phi $
is a family of supports on X such that every
$\Phi $
is a family of supports on X such that every
![]() $C\in \Phi $
has a neighbourhood D in X with
$C\in \Phi $
has a neighbourhood D in X with
![]() $D\in \Phi $
. Then the following are equivalent:
$D\in \Phi $
. Then the following are equivalent:
-
(1)
 ${\mathcal {F}}$
is
${\mathcal {F}}$
is
 $\Phi $
-soft;
$\Phi $
-soft; -
(2)
 ${\mathcal {F}}_{|S}$
is soft for every
${\mathcal {F}}_{|S}$
is soft for every
 $S\in \Phi $
;
$S\in \Phi $
; -
(3)
 $\Gamma _{\Phi }(X;{\mathcal {F}})\longrightarrow \Gamma _{\Phi _{|S}}(S; {\mathcal {F}}_{|S})$
is surjective for every closed subset S of X;If in addition X is an object of
$\Gamma _{\Phi }(X;{\mathcal {F}})\longrightarrow \Gamma _{\Phi _{|S}}(S; {\mathcal {F}}_{|S})$
is surjective for every closed subset S of X;If in addition X is an object of
 $\widetilde {{\mathfrak T}}$
and
$\widetilde {{\mathfrak T}}$
and
 $\Phi $
is a constructible family of supports on X, then the above are also equivalent to:
$\Phi $
is a constructible family of supports on X, then the above are also equivalent to: -
(4)
 ${\mathcal {F}}_{|Z}$
is soft for every constructible subset Z of X that is in
${\mathcal {F}}_{|Z}$
is soft for every constructible subset Z of X that is in
 $\Phi $
;If moreover
$\Phi $
;If moreover
 $\Phi $
is a normal and constructible family of supports on X, then the above are also equivalent to:
$\Phi $
is a normal and constructible family of supports on X, then the above are also equivalent to: -
(5)
 $\Gamma (X;{\mathcal {F}})\longrightarrow \Gamma (Z; {\mathcal {F}}_{|Z})$
is surjective for every constructible subset Z of X that is in
$\Gamma (X;{\mathcal {F}})\longrightarrow \Gamma (Z; {\mathcal {F}}_{|Z})$
is surjective for every constructible subset Z of X that is in
 $\Phi $
.
$\Phi $
.
Proof. By our hypothesis on
![]() $\Phi $
, the arguments in [Reference Bredon14, Chapter II, 9.3] show the equivalence of (1), (2) and (3). The equivalence of (2) and (4) is obvious since every
$\Phi $
, the arguments in [Reference Bredon14, Chapter II, 9.3] show the equivalence of (1), (2) and (3). The equivalence of (2) and (4) is obvious since every
![]() $S\in \Phi $
is contained in some constructible subset Z of X that is in
$S\in \Phi $
is contained in some constructible subset Z of X that is in
![]() $\Phi $
. Also, (1) implies that (5) is obvious.
$\Phi $
. Also, (1) implies that (5) is obvious.
Assume (5), and let
![]() $S\in \Phi $
and
$S\in \Phi $
and
![]() $s\in \Gamma (S; {\mathcal {F}}_{|S})$
. Since
$s\in \Gamma (S; {\mathcal {F}}_{|S})$
. Since
![]() $\Phi $
is normal and constructible, S has a fundamental system of normal and constructible closed neighbourhoods in
$\Phi $
is normal and constructible, S has a fundamental system of normal and constructible closed neighbourhoods in
![]() $\Phi. $
In particular, there is an open constructible subset V of X and a closed constructible subset D of X such that
$\Phi. $
In particular, there is an open constructible subset V of X and a closed constructible subset D of X such that
![]() $S\subseteq V\subseteq D$
and
$S\subseteq V\subseteq D$
and
![]() $D\in \Phi $
. By Lemma 3.22, s can be extended to a section
$D\in \Phi $
. By Lemma 3.22, s can be extended to a section
![]() $t\in \Gamma (W;{\mathcal {F}})$
of
$t\in \Gamma (W;{\mathcal {F}})$
of
![]() ${\mathcal F}$
over an open constructible subset W of X such that
${\mathcal F}$
over an open constructible subset W of X such that
![]() $S\subseteq W\subseteq V$
. Applying the shrinking lemma in D, we find a closed constructible neighbourhood Z of S in W. Since
$S\subseteq W\subseteq V$
. Applying the shrinking lemma in D, we find a closed constructible neighbourhood Z of S in W. Since
![]() $D\in \Phi $
, we have
$D\in \Phi $
, we have
![]() $Z\in \Phi $
. So
$Z\in \Phi $
. So
![]() $t_{|Z}\in \Gamma (Z;{\mathcal {F}}_{|Z})$
,
$t_{|Z}\in \Gamma (Z;{\mathcal {F}}_{|Z})$
,
![]() $(t_{|Z})_{|S}=s$
, and
$(t_{|Z})_{|S}=s$
, and
![]() $t_{|Z}$
can be extended to X by (5).
$t_{|Z}$
can be extended to X by (5).
The locally semi-algebraic analogue of Proposition 3.24 is [Reference Delfs17, Chapter II, Propositions 4.1 and 4.2], and the o-minimal version is [Reference Edmundo and Prelli25, Proposition 3.4].
The following topological result is often useful. It is an immediate consequence of Proposition 3.24, and we omit the proof and refer the reader to [Reference Edmundo and Prelli25, Proposition 3.6] (compare also with [Reference Bredon14, Chapter II, Propositions 9.2 and 9.12 and Corollary 9.13]).
Fact 3.25. Let X be a topological space and
![]() $\Phi $
be a family of supports on X such that every
$\Phi $
be a family of supports on X such that every
![]() $C\in \Phi $
has a neighbourhood D in X with
$C\in \Phi $
has a neighbourhood D in X with
![]() $D\in \Phi $
. Let W be a locally closed subset of X. The following hold:
$D\in \Phi $
. Let W be a locally closed subset of X. The following hold:
-
(i) If
 ${\mathcal {F}} \in \mathrm {Mod}(A_X)$
is
${\mathcal {F}} \in \mathrm {Mod}(A_X)$
is
 $\Phi $
-soft, then
$\Phi $
-soft, then
 ${\mathcal {F}}_{|W}$
is
${\mathcal {F}}_{|W}$
is
 $\Phi _{|W}$
-soft.
$\Phi _{|W}$
-soft. -
(ii)
 ${\mathcal {G}}$
in
${\mathcal {G}}$
in
 $\mathrm {Mod}(A_W)$
is
$\mathrm {Mod}(A_W)$
is
 $\Phi _{|W}$
-soft if and only if
$\Phi _{|W}$
-soft if and only if
 $i_{W!}{\mathcal {G}}$
is
$i_{W!}{\mathcal {G}}$
is
 $\Phi $
-soft.
$\Phi $
-soft. -
(iii) If
 ${\mathcal {F}}\in \mathrm {Mod}(A_X)$
is
${\mathcal {F}}\in \mathrm {Mod}(A_X)$
is
 $\Phi $
-soft, then
$\Phi $
-soft, then
 ${\mathcal {F}}_W$
is
${\mathcal {F}}_W$
is
 $\Phi $
-soft.
$\Phi $
-soft.
We now come to the main result here. Its topological analogue is [Reference Bredon14, Chapter II, 9.6, 9.9 and 9.10], and the locally semi-algebraic analogue is [Reference Delfs17, Chapter II, Propositions 4.8, 4.12 and Corollary 4.13]. The o-minimal version is [Reference Edmundo and Prelli25, Proposition 3.7] (as mentioned above, the assumption that
![]() $D\cap Y$
has a fundamental system of normal and constructible locally closed neighbourhoods in X is missing).
$D\cap Y$
has a fundamental system of normal and constructible locally closed neighbourhoods in X is missing).
Proposition 3.26. Assume that X is an object in
![]() $\widetilde {{\mathfrak T}}$
. Let Z be a subspace of
$\widetilde {{\mathfrak T}}$
. Let Z be a subspace of
![]() $X, \ \Phi $
be a normal and constructible family of supports on X and Y be a subspace of Z such that for every constructible
$X, \ \Phi $
be a normal and constructible family of supports on X and Y be a subspace of Z such that for every constructible
![]() $D\in \Phi $
,
$D\in \Phi $
,
![]() $D\cap Y$
is a quasi-compact subset of Z having a fundamental system of normal and constructible locally closed neighbourhoods in X. Then the full additive subcategory of
$D\cap Y$
is a quasi-compact subset of Z having a fundamental system of normal and constructible locally closed neighbourhoods in X. Then the full additive subcategory of
![]() $\mathrm {Mod} (A_Y)$
of
$\mathrm {Mod} (A_Y)$
of
![]() $\Phi \cap Y$
-soft sheaves is
$\Phi \cap Y$
-soft sheaves is
![]() $\Gamma _{\Phi \cap Y}(Y;\bullet )$
-injective: that is,
$\Gamma _{\Phi \cap Y}(Y;\bullet )$
-injective: that is,
-
(1) For every
 ${\mathcal {F}}\in \mathrm {Mod} (A_Y)$
, there exists a
${\mathcal {F}}\in \mathrm {Mod} (A_Y)$
, there exists a
 $\Phi \cap Y$
-soft
$\Phi \cap Y$
-soft
 ${\mathcal {F}}'\in \mathrm {Mod} (A_Y)$
and an exact sequence
${\mathcal {F}}'\in \mathrm {Mod} (A_Y)$
and an exact sequence
 $0\rightarrow {\mathcal {F}}\rightarrow {\mathcal {F}}'$
.
$0\rightarrow {\mathcal {F}}\rightarrow {\mathcal {F}}'$
. -
(2) If
 $0\rightarrow {\mathcal {F}}'\stackrel {\alpha }\rightarrow {\mathcal {F}}\stackrel {\beta }\rightarrow {\mathcal {F}}" \rightarrow 0$
is an exact sequence in
$0\rightarrow {\mathcal {F}}'\stackrel {\alpha }\rightarrow {\mathcal {F}}\stackrel {\beta }\rightarrow {\mathcal {F}}" \rightarrow 0$
is an exact sequence in
 $\mathrm {Mod} (A_Y)$
and
$\mathrm {Mod} (A_Y)$
and
 ${\mathcal {F}}'$
is
${\mathcal {F}}'$
is
 $\Phi \cap Y$
-soft, then is an exact sequence.
$\Phi \cap Y$
-soft, then is an exact sequence. $$\begin{align*}0\longrightarrow \Gamma _{\Phi \cap Y}(Y;{\mathcal{F}}')\stackrel{\alpha}\longrightarrow \Gamma _{\Phi \cap Y}(Y;{\mathcal{F}})\stackrel{\beta}\longrightarrow \Gamma _{\Phi \cap Y}(Y;{\mathcal{F}}")\longrightarrow 0 \end{align*}$$
$$\begin{align*}0\longrightarrow \Gamma _{\Phi \cap Y}(Y;{\mathcal{F}}')\stackrel{\alpha}\longrightarrow \Gamma _{\Phi \cap Y}(Y;{\mathcal{F}})\stackrel{\beta}\longrightarrow \Gamma _{\Phi \cap Y}(Y;{\mathcal{F}}")\longrightarrow 0 \end{align*}$$
-
(3) If
 $0\rightarrow {\mathcal {F}}'\rightarrow {\mathcal {F}}\rightarrow {\mathcal {F}}" \rightarrow 0$
is an exact sequence in
$0\rightarrow {\mathcal {F}}'\rightarrow {\mathcal {F}}\rightarrow {\mathcal {F}}" \rightarrow 0$
is an exact sequence in
 $\mathrm {Mod}(A_Y)$
and
$\mathrm {Mod}(A_Y)$
and
 ${\mathcal {F}}'$
and
${\mathcal {F}}'$
and
 ${\mathcal {F}}$
are
${\mathcal {F}}$
are
 $\Phi \cap Y$
-soft, then
$\Phi \cap Y$
-soft, then
 ${\mathcal {F}}"$
is
${\mathcal {F}}"$
is
 $\Phi \cap Y$
-soft.
$\Phi \cap Y$
-soft.
Proof. Point (1) follows since on any topological space
![]() $Y,$
the full additive subcategory of
$Y,$
the full additive subcategory of
![]() $\mathrm {Mod}(A_Y)$
of injective (and flabby) A-sheaves is co-generating (see, for example, [Reference Kashiwara and Schapira39, Proposition 2.4.3]) and injective A-sheaves are flabby, so
$\mathrm {Mod}(A_Y)$
of injective (and flabby) A-sheaves is co-generating (see, for example, [Reference Kashiwara and Schapira39, Proposition 2.4.3]) and injective A-sheaves are flabby, so
![]() $\Phi \cap Y$
-soft by Lemma 3.23. On the other hand, (3) follows as usual from (2) by a simple diagram chase using Proposition 3.24 (3).
$\Phi \cap Y$
-soft by Lemma 3.23. On the other hand, (3) follows as usual from (2) by a simple diagram chase using Proposition 3.24 (3).
We now prove (2). Let
![]() $s" \in \Gamma _{\Phi \cap Y}(Y,{\mathcal {F}}")$
. We have to find
$s" \in \Gamma _{\Phi \cap Y}(Y,{\mathcal {F}}")$
. We have to find
![]() $s \in \Gamma _{\Phi \cap Y}(Y,{\mathcal {F}})$
such that
$s \in \Gamma _{\Phi \cap Y}(Y,{\mathcal {F}})$
such that
![]() $\beta (s)=s"$
. Since
$\beta (s)=s"$
. Since
![]() $\Phi $
is normal and constructible, there exist an open constructible subset U of X and a closed constructible subset C of X such that
$\Phi $
is normal and constructible, there exist an open constructible subset U of X and a closed constructible subset C of X such that
![]() $\mathrm {supp}\,s" \subseteq U\subseteq C$
and
$\mathrm {supp}\,s" \subseteq U\subseteq C$
and
![]() $C \in \Phi $
.
$C \in \Phi $
.
Suppose there is
![]() $t\in \Gamma (C\cap Y; {\mathcal {F}})$
such that
$t\in \Gamma (C\cap Y; {\mathcal {F}})$
such that
![]() $\beta (t)=s^{\prime \prime }_{\,\,|C\cap Y}$
. Then
$\beta (t)=s^{\prime \prime }_{\,\,|C\cap Y}$
. Then
![]() $\beta (t_{|(C\setminus U)\cap Y})=0,$
so
$\beta (t_{|(C\setminus U)\cap Y})=0,$
so
![]() $t_{|(C\setminus U)\cap Y}=\alpha (s')$
for some
$t_{|(C\setminus U)\cap Y}=\alpha (s')$
for some
![]() $s'\in \Gamma ((C\setminus U)\cap Y;{\mathcal {F}}')$
. Since
$s'\in \Gamma ((C\setminus U)\cap Y;{\mathcal {F}}')$
. Since
![]() ${\mathcal {F}}'$
is
${\mathcal {F}}'$
is
![]() $\Phi \cap Y$
-soft,
$\Phi \cap Y$
-soft,
![]() $s'$
can be extended to a section
$s'$
can be extended to a section
![]() $s'\in \Gamma (C\cap Y; {\mathcal {F}}')$
. Then
$s'\in \Gamma (C\cap Y; {\mathcal {F}}')$
. Then
![]() $(t-\alpha (s'))_{|(C\setminus U)\cap Y}=0$
and so can be extended, by
$(t-\alpha (s'))_{|(C\setminus U)\cap Y}=0$
and so can be extended, by
![]() $0,$
to a section
$0,$
to a section
![]() $s\in \Gamma (Y;{\mathcal {F}})$
with
$s\in \Gamma (Y;{\mathcal {F}})$
with
![]() $\mathrm {supp} \,s\subseteq C\cap Y\in \Phi \cap Y$
and
$\mathrm {supp} \,s\subseteq C\cap Y\in \Phi \cap Y$
and
![]() $\beta (s)=s"$
.
$\beta (s)=s"$
.
Now, considering the exact sequence
since by Fact 3.25 (iii)
![]() ${\mathcal {F}}^{\prime }_{C \cap Y}$
is still
${\mathcal {F}}^{\prime }_{C \cap Y}$
is still
![]() $\Phi \cap Y$
-soft, replacing
$\Phi \cap Y$
-soft, replacing
![]() ${\mathcal {F}}',{\mathcal {F}},{\mathcal {F}}"$
with
${\mathcal {F}}',{\mathcal {F}},{\mathcal {F}}"$
with
![]() ${\mathcal {F}}^{\prime }_{C \cap Y}, \ {\mathcal {F}}_{C \cap Y}$
and
${\mathcal {F}}^{\prime }_{C \cap Y}, \ {\mathcal {F}}_{C \cap Y}$
and
![]() ${\mathcal {F}}^{\prime \prime }_{C\cap Y}$
, respectively, we are reduced to proving that the sequence
${\mathcal {F}}^{\prime \prime }_{C\cap Y}$
, respectively, we are reduced to proving that the sequence
is exact.
Let
![]() $s" \in \Gamma (C\cap Y;{\mathcal {F}}")$
. There is a covering
$s" \in \Gamma (C\cap Y;{\mathcal {F}}")$
. There is a covering
![]() $\{U_j:j\in J\}$
of
$\{U_j:j\in J\}$
of
![]() $C\cap Y$
by open constructible subsets of X and sections
$C\cap Y$
by open constructible subsets of X and sections
![]() $s_j\in \Gamma (U_j\cap (C\cap Y); {\mathcal {F}})$
,
$s_j\in \Gamma (U_j\cap (C\cap Y); {\mathcal {F}})$
,
![]() $j\in J$
, such that
$j\in J$
, such that
![]() $\beta (s_{j})=s^{\prime \prime }_{\,\,|U_j\cap (C\cap Y)}$
. By the assumptions on
$\beta (s_{j})=s^{\prime \prime }_{\,\,|U_j\cap (C\cap Y)}$
. By the assumptions on
![]() $C\cap Y$
, we can assume that J is finite, so
$C\cap Y$
, we can assume that J is finite, so
![]() $\cup \{U_j:j\in J\}$
is an open constructible subset of
$\cup \{U_j:j\in J\}$
is an open constructible subset of
![]() $X,$
and furthermore, there are an open constructible subset
$X,$
and furthermore, there are an open constructible subset
![]() $O'$
in X and a normal, constructible locally closed subset
$O'$
in X and a normal, constructible locally closed subset
![]() $X'$
in X such that
$X'$
in X such that
![]() $C\cap Y\subseteq O'\subseteq X'\subseteq \cup \{U_j:j\in J\}$
. For each
$C\cap Y\subseteq O'\subseteq X'\subseteq \cup \{U_j:j\in J\}$
. For each
![]() $j\in J$
, let
$j\in J$
, let
![]() $U^{\prime }_j=U_j\cap X'$
. Since
$U^{\prime }_j=U_j\cap X'$
. Since
![]() $X'$
is normal and constructible, by the shrinking lemma, there are open constructible subsets
$X'$
is normal and constructible, by the shrinking lemma, there are open constructible subsets
![]() $\{V^{\prime }_j:j\in J\}$
of
$\{V^{\prime }_j:j\in J\}$
of
![]() $X'$
and closed constructible subsets
$X'$
and closed constructible subsets
![]() $\{K^{\prime }_j:j\in J\}$
of
$\{K^{\prime }_j:j\in J\}$
of
![]() $X'$
such that
$X'$
such that
![]() $V^{\prime }_j\subseteq K^{\prime }_j\subseteq U^{\prime }_j$
for every
$V^{\prime }_j\subseteq K^{\prime }_j\subseteq U^{\prime }_j$
for every
![]() $j\in J$
and
$j\in J$
and
![]() $X'= \cup \{V^{\prime }_j:j\in J\}$
. Now we may replace X by a constructible open subset and assume that
$X'= \cup \{V^{\prime }_j:j\in J\}$
. Now we may replace X by a constructible open subset and assume that
![]() $X'$
is a constructible closed subset of X. For each
$X'$
is a constructible closed subset of X. For each
![]() $j\in J$
, let
$j\in J$
, let
![]() $V_j=V^{\prime }_j\cap O'$
and
$V_j=V^{\prime }_j\cap O'$
and
![]() $K_j=K^{\prime }_j$
. Then for each
$K_j=K^{\prime }_j$
. Then for each
![]() $j\in J, \ V_j$
is an open constructible subset of X and
$j\in J, \ V_j$
is an open constructible subset of X and
![]() $K_j$
is a closed constructible subset of X with
$K_j$
is a closed constructible subset of X with
![]() $V_j\subseteq K_j\subseteq U_j$
and
$V_j\subseteq K_j\subseteq U_j$
and
![]() $C\cap Y\subseteq \cup \{V_j:j\in J\}$
.
$C\cap Y\subseteq \cup \{V_j:j\in J\}$
.
We now proceed by induction on
![]() $\#J$
. Suppose that
$\#J$
. Suppose that
![]() $J=I\cup \{j\}$
, and let
$J=I\cup \{j\}$
, and let
![]() $V_I=\cup \{V_i:i\in I\}, \ K_I=\cup \{K_i:i\in I\}$
and
$V_I=\cup \{V_i:i\in I\}, \ K_I=\cup \{K_i:i\in I\}$
and
![]() $U_I=\cup \{U_i:i\in I\}$
. By induction hypothesis, let
$U_I=\cup \{U_i:i\in I\}$
. By induction hypothesis, let
![]() $s_I\in \Gamma (K_I\cap (C\cap Y); {\mathcal {F}})$
be such that
$s_I\in \Gamma (K_I\cap (C\cap Y); {\mathcal {F}})$
be such that
![]() $\beta (s_{I})=s^{\prime \prime }_{\,\,|K_I\cap (C\cap Y)}$
. Since
$\beta (s_{I})=s^{\prime \prime }_{\,\,|K_I\cap (C\cap Y)}$
. Since
![]() $\beta ((s_I-s_j)_{|K_I\cap K_j})=0,$
there is
$\beta ((s_I-s_j)_{|K_I\cap K_j})=0,$
there is
![]() $s'\in \Gamma (K_I \cap K_j\cap (C\cap Y);{\mathcal {F}}')$
such that
$s'\in \Gamma (K_I \cap K_j\cap (C\cap Y);{\mathcal {F}}')$
such that
![]() $\alpha (s')=(s_I-s_j)_{|K_I\cap K_j}$
that extends to
$\alpha (s')=(s_I-s_j)_{|K_I\cap K_j}$
that extends to
![]() $s' \in \Gamma (C\cap Y;{\mathcal {F}}')$
since
$s' \in \Gamma (C\cap Y;{\mathcal {F}}')$
since
![]() ${\mathcal {F}}'$
is
${\mathcal {F}}'$
is
![]() $\Phi \cap Y$
-soft. Replacing
$\Phi \cap Y$
-soft. Replacing
![]() $s_I$
with
$s_I$
with
![]() $s_I-\alpha (s^{\prime }_{\,|K_I\cap (C\cap Y)})$
, we may suppose that
$s_I-\alpha (s^{\prime }_{\,|K_I\cap (C\cap Y)})$
, we may suppose that
![]() $s_I=s_j$
on
$s_I=s_j$
on
![]() $K_I \cap K_j\cap (C\cap Y)$
. Then since
$K_I \cap K_j\cap (C\cap Y)$
. Then since
![]() $(K_I\cup K_j)\cap (C\cap Y)= C\cap Y,$
there exists
$(K_I\cup K_j)\cap (C\cap Y)= C\cap Y,$
there exists
![]() $s \in \Gamma (C\cap Y;{\mathcal {F}})$
such that
$s \in \Gamma (C\cap Y;{\mathcal {F}})$
such that
![]() $s_{| K_I\cap (C\cap Y)}=s_I$
and
$s_{| K_I\cap (C\cap Y)}=s_I$
and
![]() $s_{|K_j\cap (C\cap Y)}=s_j$
. Thus the induction proceeds.
$s_{|K_j\cap (C\cap Y)}=s_j$
. Thus the induction proceeds.
We now include several corollaries that will be useful later.
Corollary 3.27. Assume that X is an object in
![]() $\widetilde {{\mathfrak T}}$
. Suppose either that
$\widetilde {{\mathfrak T}}$
. Suppose either that
![]() $\Phi $
is a normal and constructible family of supports on X and Z is a (constructible) locally closed subset of X or that
$\Phi $
is a normal and constructible family of supports on X and Z is a (constructible) locally closed subset of X or that
![]() $\Phi $
is any family of supports on X and Z is a closed subset of X. If
$\Phi $
is any family of supports on X and Z is a closed subset of X. If
![]() ${\mathcal {F}}\in \mathrm {Mod} (A_Z)$
, then
${\mathcal {F}}\in \mathrm {Mod} (A_Z)$
, then
Proof. The second case is covered by [Reference Bredon14, Chapter II, 10.1]. If Z is closed in an open subset U of X, then
![]() $\Phi _{|U}$
is a normal and constructible family of supports on U and
$\Phi _{|U}$
is a normal and constructible family of supports on U and
![]() $\Phi _{|Z}=\Phi _{|U}\cap Z$
. In particular, if
$\Phi _{|Z}=\Phi _{|U}\cap Z$
. In particular, if
![]() $D\in \Phi _{|U},$
then
$D\in \Phi _{|U},$
then
![]() $D\cap Z\in \Phi _{|U}$
, so
$D\cap Z\in \Phi _{|U}$
, so
![]() $D\cap Z$
is a quasi-compact subset of Z having a fundamental system of normal and constructible locally closed neighbourhoods in U. Now the result follows from Proposition 3.26, Fact 3.25 (ii) and the fact that
$D\cap Z$
is a quasi-compact subset of Z having a fundamental system of normal and constructible locally closed neighbourhoods in U. Now the result follows from Proposition 3.26, Fact 3.25 (ii) and the fact that
![]() $\Gamma _{\Phi }(X;i_{Z!}{\mathcal {F}})\simeq \Gamma _{\Phi |Z}(Z;{\mathcal {F}})$
([Reference Bredon14, Chapter I, Proposition 6.6]).
$\Gamma _{\Phi }(X;i_{Z!}{\mathcal {F}})\simeq \Gamma _{\Phi |Z}(Z;{\mathcal {F}})$
([Reference Bredon14, Chapter I, Proposition 6.6]).
It also follows that if
![]() $X, \ Z, Y$
and
$X, \ Z, Y$
and
![]() $\Phi $
are as in Proposition 3.26, then
$\Phi $
are as in Proposition 3.26, then
![]() $H^q_{\Phi \cap Y}(Y; {\mathcal {G}} )$
is the qth cohomology of the cochain complex
$H^q_{\Phi \cap Y}(Y; {\mathcal {G}} )$
is the qth cohomology of the cochain complex
where
is a resolution of
![]() ${\mathcal {G}} $
by
${\mathcal {G}} $
by
![]() $\Phi \cap Y$
-soft sheaves in
$\Phi \cap Y$
-soft sheaves in
![]() $\mathrm {Mod} (A_Y)$
.
$\mathrm {Mod} (A_Y)$
.
Moreover, if
![]() ${\mathcal {G}}$
is any flabby sheaf in
${\mathcal {G}}$
is any flabby sheaf in
![]() $\mathrm {Mod} (A_X)$
, then the restriction
$\mathrm {Mod} (A_X)$
, then the restriction
![]() $\Gamma _{\Phi }(X; {\mathcal {G}})\to \Gamma _{\Phi \cap Y}(Y;{\mathcal {G}} _{|Y})$
is surjective (by Lemma 3.23) and
$\Gamma _{\Phi }(X; {\mathcal {G}})\to \Gamma _{\Phi \cap Y}(Y;{\mathcal {G}} _{|Y})$
is surjective (by Lemma 3.23) and
![]() $H^p_{\Phi \cap Y}(Y;{\mathcal {G}}_{|Y})=0$
for all
$H^p_{\Phi \cap Y}(Y;{\mathcal {G}}_{|Y})=0$
for all
![]() $p>0$
(since
$p>0$
(since
![]() ${\mathcal {G}} _{|Y}$
is
${\mathcal {G}} _{|Y}$
is
![]() $\Phi \cap Y$
-soft by Lemma 3.22). This means Y is
$\Phi \cap Y$
-soft by Lemma 3.22). This means Y is
![]() $\Phi $
-taut in X (see [Reference Bredon14, Chapter II, Definition 10.5]).
$\Phi $
-taut in X (see [Reference Bredon14, Chapter II, Definition 10.5]).
Since on any topological space X an open subset is
![]() $\Psi $
-taut in X for any family of supports
$\Psi $
-taut in X for any family of supports
![]() $\Psi $
on
$\Psi $
on
![]() $X,$
it follows from [Reference Bredon14, Chapter II, Theorem 10.6] that:
$X,$
it follows from [Reference Bredon14, Chapter II, Theorem 10.6] that:
Corollary 3.28. Assume that X is an object in
![]() $\widetilde {{\mathfrak T}}$
. Let Z be a subspace of
$\widetilde {{\mathfrak T}}$
. Let Z be a subspace of
![]() $X, \ \Phi $
a normal and constructible family of supports on X and Y a subspace of Z such that for every constructible
$X, \ \Phi $
a normal and constructible family of supports on X and Y a subspace of Z such that for every constructible
![]() $D\in \Phi , \ D\cap Y$
is a quasi-compact subset of Z having a fundamental system of normal and constructible locally closed neighbourhoods in X. Then for every
$D\in \Phi , \ D\cap Y$
is a quasi-compact subset of Z having a fundamental system of normal and constructible locally closed neighbourhoods in X. Then for every
![]() ${\mathcal {G}}\in \mathrm {Mod} (A_Z)$
, the canonical homomorphism
${\mathcal {G}}\in \mathrm {Mod} (A_Z)$
, the canonical homomorphism
where U ranges through the family of open constructible subsets of X containing Y, is an isomorphism for every
![]() $q\geq 0$
.
$q\geq 0$
.
For the locally semi-algebraic analogue of the above, compare with [Reference Delfs17, Chapter II, Theorem 5.2].
Since fibres of morphisms in
![]() $\widetilde {{\mathfrak T}}$
are quasi-compact (Remark 3.10), applying Corollary 3.28, we obtain the following result (compare with [Reference Delfs17, Chapter II, Theorem 7.1]).
$\widetilde {{\mathfrak T}}$
are quasi-compact (Remark 3.10), applying Corollary 3.28, we obtain the following result (compare with [Reference Delfs17, Chapter II, Theorem 7.1]).
Theorem 3.29 (Base change formula).
Let
![]() $f\colon X\to Y$
be a morphism in
$f\colon X\to Y$
be a morphism in
![]() $\widetilde {{\mathfrak T}}$
. Assume that f maps constructible closed subsets of X to closed subsets of Y and that every
$\widetilde {{\mathfrak T}}$
. Assume that f maps constructible closed subsets of X to closed subsets of Y and that every
![]() $\alpha \in Y$
has an open constructible neighbourhood W in Y such that
$\alpha \in Y$
has an open constructible neighbourhood W in Y such that
![]() $\alpha $
is closed in W and
$\alpha $
is closed in W and
![]() $f^{-1}(W)$
is a normal and constructible subset of X. Let
$f^{-1}(W)$
is a normal and constructible subset of X. Let
![]() ${\mathcal {F}} \in \mathrm {Mod} (A_X)$
. Then for every
${\mathcal {F}} \in \mathrm {Mod} (A_X)$
. Then for every
![]() $\alpha \in Y,$
the canonical homomorphism
$\alpha \in Y,$
the canonical homomorphism
is an isomorphism for every
![]() $q\geq 0$
.
$q\geq 0$
.
Proof. Fix
![]() $\alpha \in Y$
. First, notice that
$\alpha \in Y$
. First, notice that
is a fundamental system of open neighbourhoods of
![]() $f^{-1}(\alpha )$
. Indeed, let U be an open neighbourhood of
$f^{-1}(\alpha )$
. Indeed, let U be an open neighbourhood of
![]() $f^{-1}(\alpha )$
. Since
$f^{-1}(\alpha )$
. Since
![]() $f^{-1}(\alpha )$
is quasi-compact, we may assume that U is an open constructible neighbourhood of
$f^{-1}(\alpha )$
is quasi-compact, we may assume that U is an open constructible neighbourhood of
![]() $f^{-1}(\alpha )$
. Then by assumption,
$f^{-1}(\alpha )$
. Then by assumption,
![]() $f(X\setminus U)$
is a closed subset of Y not containing
$f(X\setminus U)$
is a closed subset of Y not containing
![]() $\alpha $
. Let V be an open constructible neighbourhood of
$\alpha $
. Let V be an open constructible neighbourhood of
![]() $\alpha $
in W contained in
$\alpha $
in W contained in
![]() $Y\setminus f(X\setminus U)$
. Then
$Y\setminus f(X\setminus U)$
. Then
![]() $f^{-1}(V)\subseteq U$
.
$f^{-1}(V)\subseteq U$
.
Also notice that
![]() $R^qf_*{\mathcal {F}}$
is the sheaf associated to the presheaf sending V to
$R^qf_*{\mathcal {F}}$
is the sheaf associated to the presheaf sending V to
![]() $H^q(f^{-1}(V);{\mathcal {F}})$
. So
$H^q(f^{-1}(V);{\mathcal {F}})$
. So
 $$\begin{align*}(R^qf_*{\mathcal{F}})_{\alpha }=\underset{\alpha \subseteq V\subseteq W}{\underrightarrow{\lim}}H^q(f^{-1}(V);{\mathcal{F}})=\underset{f^{-1}(\alpha )\subseteq U}{\underrightarrow{\lim}}H^q(U;{\mathcal{F}}),\end{align*}$$
$$\begin{align*}(R^qf_*{\mathcal{F}})_{\alpha }=\underset{\alpha \subseteq V\subseteq W}{\underrightarrow{\lim}}H^q(f^{-1}(V);{\mathcal{F}})=\underset{f^{-1}(\alpha )\subseteq U}{\underrightarrow{\lim}}H^q(U;{\mathcal{F}}),\end{align*}$$
where V (respectively, U) ranges through the family of open constructible subsets of Y (respectively, X).
Now, by assumption,
![]() $\alpha \in W$
is closed in W and
$\alpha \in W$
is closed in W and
![]() $f^{-1}(W)$
is an open normal and constructible subset of X containing
$f^{-1}(W)$
is an open normal and constructible subset of X containing
![]() $f^{-1}(\alpha )$
. So the family of all closed subsets of
$f^{-1}(\alpha )$
. So the family of all closed subsets of
![]() $f^{-1}(W)$
is a normal and constructible family of supports on
$f^{-1}(W)$
is a normal and constructible family of supports on
![]() $f^{-1}(W)$
(Example 3.20); and since
$f^{-1}(W)$
(Example 3.20); and since
![]() $f^{-1}(\alpha )$
is closed in
$f^{-1}(\alpha )$
is closed in
![]() $f^{-1}(W),$
for every constructible closed subset
$f^{-1}(W),$
for every constructible closed subset
![]() $D\subseteq f^{-1}(W)$
,
$D\subseteq f^{-1}(W)$
,
![]() $D\cap f^{-1}(\alpha )$
is a quasi-compact subset of
$D\cap f^{-1}(\alpha )$
is a quasi-compact subset of
![]() $f^{-1}(W)$
having a fundamental system of normal and constructible locally closed neighbourhoods in
$f^{-1}(W)$
having a fundamental system of normal and constructible locally closed neighbourhoods in
![]() $f^{-1}(W)$
.
$f^{-1}(W)$
.
Therefore the result follows from Corollary 3.28 applied to
![]() $X=Z=f^{-1}(W)$
,
$X=Z=f^{-1}(W)$
,
![]() $\Phi $
the family of all closed subsets of
$\Phi $
the family of all closed subsets of
![]() $f^{-1}(W)$
and
$f^{-1}(W)$
and
![]() $Y=f^{-1}(\alpha )$
.
$Y=f^{-1}(\alpha )$
.
Using classical arguments, the Base change formula implies the following form of the Vietoris-Begle theorem:
Theorem 3.30 (Vietoris-Begle theorem).
Let
![]() $f\colon X\longrightarrow Y$
be a surjective morphism in
$f\colon X\longrightarrow Y$
be a surjective morphism in
![]() ${\mathfrak T}$
. Assume that f maps constructible closed subsets of X onto closed subsets of Y and that every
${\mathfrak T}$
. Assume that f maps constructible closed subsets of X onto closed subsets of Y and that every
![]() $\alpha \in Y$
has an open constructible neighbourhood W in Y such that
$\alpha \in Y$
has an open constructible neighbourhood W in Y such that
![]() $\alpha $
is closed in W and
$\alpha $
is closed in W and
![]() $f^{-1}(W)$
is a normal and constructible subset of X. Let
$f^{-1}(W)$
is a normal and constructible subset of X. Let
![]() ${\mathcal {F}}\in \mathrm {Mod} (A_Y),$
and suppose that
${\mathcal {F}}\in \mathrm {Mod} (A_Y),$
and suppose that
![]() $f^{-1}({\alpha })$
is connected and
$f^{-1}({\alpha })$
is connected and
![]() $H^q(f^{-1}({\alpha }); f^{-1}{\mathcal {F}}_{|f^{-1}({\alpha })}) \ =0$
for
$H^q(f^{-1}({\alpha }); f^{-1}{\mathcal {F}}_{|f^{-1}({\alpha })}) \ =0$
for
![]() $q>0$
and all
$q>0$
and all
![]() $\alpha \in Y$
. Then for any constructible family of supports
$\alpha \in Y$
. Then for any constructible family of supports
![]() $\Psi $
on Y, the induced map
$\Psi $
on Y, the induced map
is an isomorphism.
Proof. The homomorphism
![]() $f^*\colon H^*_{\Psi }(Y;{\mathcal {F}})\longrightarrow H^*_{f^{-1}\Psi }(X;f^{-1}{\mathcal {F}})$
is the composition
$f^*\colon H^*_{\Psi }(Y;{\mathcal {F}})\longrightarrow H^*_{f^{-1}\Psi }(X;f^{-1}{\mathcal {F}})$
is the composition
![]() $\epsilon \circ \eta $
, where
$\epsilon \circ \eta $
, where
is the canonical edge homomorphism
![]() $E_2^{*,0}\to E^*$
in the Leray spectral sequence
$E_2^{*,0}\to E^*$
in the Leray spectral sequence
of
![]() $f^{-1}{\mathcal {F}}$
with respect to f and
$f^{-1}{\mathcal {F}}$
with respect to f and
![]() $\eta \colon H^*_{\Psi }(Y;{\mathcal {F}})\to H^*_{f^{-1}\Psi }(X;f_*(f^{-1}{\mathcal {F}}))$
is induced by the canonical adjunction homomorphism
$\eta \colon H^*_{\Psi }(Y;{\mathcal {F}})\to H^*_{f^{-1}\Psi }(X;f_*(f^{-1}{\mathcal {F}}))$
is induced by the canonical adjunction homomorphism
By Theorem 3.29 and the hypothesis,
![]() $R^qf_*(f^{-1}{\mathcal {F}})=0$
for all
$R^qf_*(f^{-1}{\mathcal {F}})=0$
for all
![]() $q>0$
, so the Leray sequence splits and
$q>0$
, so the Leray sequence splits and
![]() $\epsilon $
is an isomorphism. On the other hand, by Theorem 3.29 and since
$\epsilon $
is an isomorphism. On the other hand, by Theorem 3.29 and since
![]() $f^{-1}(\alpha )$
is connected, we have
$f^{-1}(\alpha )$
is connected, we have
 $$ \begin{align*} (f_*f^{-1}{\mathcal{F}})_{\alpha } &= (R^0f_*f^{-1}{\mathcal{F}})_{\alpha }\\ &\simeq H^0(f^{-1}(\alpha ); (f^{-1}{\mathcal{F}})_{|f^{-1}(\alpha )})\\ &\simeq H^0(f^{-1}(\alpha ); {\mathcal{F}}_{\alpha })\\ &\simeq {\mathcal{F}} _{\alpha}. \end{align*} $$
$$ \begin{align*} (f_*f^{-1}{\mathcal{F}})_{\alpha } &= (R^0f_*f^{-1}{\mathcal{F}})_{\alpha }\\ &\simeq H^0(f^{-1}(\alpha ); (f^{-1}{\mathcal{F}})_{|f^{-1}(\alpha )})\\ &\simeq H^0(f^{-1}(\alpha ); {\mathcal{F}}_{\alpha })\\ &\simeq {\mathcal{F}} _{\alpha}. \end{align*} $$
Hence adjunction homomorphism
![]() ${\mathcal {F}} \to f_*f^{-1}{\mathcal {F}}$
is an isomorphism and
${\mathcal {F}} \to f_*f^{-1}{\mathcal {F}}$
is an isomorphism and
![]() $\eta $
is also an isomorphism.
$\eta $
is also an isomorphism.
We end this section with the following, which follows quickly from previous results exactly the same way as its topological analogue ([Reference Bredon14, Chapter II, 16.1]):
Proposition 3.31. Assume that X is an object in
![]() $\widetilde {{\mathfrak T}}$
,
$\widetilde {{\mathfrak T}}$
,
![]() $\Phi $
is a normal and constructible family of supports on X and
$\Phi $
is a normal and constructible family of supports on X and
![]() ${\mathcal F}$
is a sheaf in
${\mathcal F}$
is a sheaf in
![]() $\mathrm {Mod} (A_X)$
. Then the following are equivalent:
$\mathrm {Mod} (A_X)$
. Then the following are equivalent:
-
(1)
 ${\mathcal F}$
is
${\mathcal F}$
is
 $\Phi $
-soft.
$\Phi $
-soft. -
(2)
 ${\mathcal F}_U$
is
${\mathcal F}_U$
is
 $\Gamma _{\Phi }$
-acyclic for all open and constructible
$\Gamma _{\Phi }$
-acyclic for all open and constructible
 $U\subseteq X$
.
$U\subseteq X$
. -
(3)
 $H^1_{\Phi }(X;{\mathcal F}_U)=0$
for all open and constructible
$H^1_{\Phi }(X;{\mathcal F}_U)=0$
for all open and constructible
 $U\subseteq X$
.
$U\subseteq X$
. -
(4)
 $H^1_{\Phi |U}(U,{\mathcal F}_{|U})=0$
for all open and constructible
$H^1_{\Phi |U}(U,{\mathcal F}_{|U})=0$
for all open and constructible
 $U\subseteq X$
.
$U\subseteq X$
.
Proof. (1)
![]() $\Rightarrow $
(2) follows from Proposition 3.26 and Fact 3.25 (iii). (2)
$\Rightarrow $
(2) follows from Proposition 3.26 and Fact 3.25 (iii). (2)
![]() $\Rightarrow $
(3) is trivial. (3) is equivalent to (4) by Corollary 3.27. For (4)
$\Rightarrow $
(3) is trivial. (3) is equivalent to (4) by Corollary 3.27. For (4)
![]() $\Rightarrow $
(1), consider a constructible closed set C in
$\Rightarrow $
(1), consider a constructible closed set C in
![]() $\Phi $
and the exact sequence
$\Phi $
and the exact sequence
![]() $0\longrightarrow {\mathcal F}_{X\setminus C}\longrightarrow {\mathcal F}\longrightarrow {\mathcal F}_C\longrightarrow 0$
. The associated long exact cohomology sequence
$0\longrightarrow {\mathcal F}_{X\setminus C}\longrightarrow {\mathcal F}\longrightarrow {\mathcal F}_C\longrightarrow 0$
. The associated long exact cohomology sequence
shows that
![]() $\Gamma _{\Phi }(X;{\mathcal F})\longrightarrow \Gamma _{\Phi |C}(X;{\mathcal F}_{|C})$
is surjective. Hence
$\Gamma _{\Phi }(X;{\mathcal F})\longrightarrow \Gamma _{\Phi |C}(X;{\mathcal F}_{|C})$
is surjective. Hence
![]() ${\mathcal F}$
is
${\mathcal F}$
is
![]() $\Phi $
-soft by Proposition 3.24 (5).
$\Phi $
-soft by Proposition 3.24 (5).
4 A site on definable sets in
 ${\mathbf {\Gamma }_{\infty } }$
${\mathbf {\Gamma }_{\infty } }$
We will assume some familiarity with o-minimality. We refer the reader to classical texts like [Reference van den Dries53]. Note that we allow o-minimal structures to have end points, which is a subtle difference from [Reference van den Dries53]. Most results from [Reference van den Dries53] still hold in this context.
Let
![]() ${\mathbf {\Gamma }}=({\Gamma } , < , \ldots )$
be an o-minimal structure without end points. Let
${\mathbf {\Gamma }}=({\Gamma } , < , \ldots )$
be an o-minimal structure without end points. Let
![]() $\infty $
be a new symbol, and set
$\infty $
be a new symbol, and set
![]() ${\Gamma _{\infty } }={\Gamma } \cup \{\infty \}$
with
${\Gamma _{\infty } }={\Gamma } \cup \{\infty \}$
with
![]() $x<\infty $
for all
$x<\infty $
for all
![]() $x\in {\Gamma }$
. The example that we have in mind is the case where
$x\in {\Gamma }$
. The example that we have in mind is the case where
![]() ${\mathbf {\Gamma }}=({\Gamma }, <, +)$
is the value group of algebraically closed field and
${\mathbf {\Gamma }}=({\Gamma }, <, +)$
is the value group of algebraically closed field and
![]() $\infty $
is the valuation of
$\infty $
is the valuation of
![]() $0$
.
$0$
.
When
![]() $({\Gamma }, <)$
is nonarchimedean as a linear order (i.e., does not embed into the reals), then infinite definable sets in the structure
$({\Gamma }, <)$
is nonarchimedean as a linear order (i.e., does not embed into the reals), then infinite definable sets in the structure
![]() ${\mathbf {\Gamma }_{\infty } }$
induced by
${\mathbf {\Gamma }_{\infty } }$
induced by
![]() ${\mathbf {\Gamma }}$
on
${\mathbf {\Gamma }}$
on
![]() ${\Gamma _{\infty } }$
with their natural topology are in general totally disconnected and not locally compact. The goals in this section are (i) to introduce an appropriate site that will replace the topology just mentioned and show that definable sets with this site are
${\Gamma _{\infty } }$
with their natural topology are in general totally disconnected and not locally compact. The goals in this section are (i) to introduce an appropriate site that will replace the topology just mentioned and show that definable sets with this site are
![]() ${\mathcal {T}}$
-spaces (Subsection 4.1); and (ii) to show that for the associated notion of
${\mathcal {T}}$
-spaces (Subsection 4.1); and (ii) to show that for the associated notion of
![]() ${\mathcal {T}}$
-normality, when
${\mathcal {T}}$
-normality, when
![]() ${\mathbf {\Gamma }}$
is an o-minimal expansion of an ordered group,
${\mathbf {\Gamma }}$
is an o-minimal expansion of an ordered group,
![]() ${\mathcal {T}}$
-locally closed subsets are finite unions of
${\mathcal {T}}$
-locally closed subsets are finite unions of
![]() ${\mathcal {T}}$
-open subsets that are
${\mathcal {T}}$
-open subsets that are
![]() ${\mathcal {T}}$
-normal (Subsection 4.2). We point out that normality in
${\mathcal {T}}$
-normal (Subsection 4.2). We point out that normality in
![]() ${\mathbf {\Gamma }_{\infty } }$
is more complicated than in
${\mathbf {\Gamma }_{\infty } }$
is more complicated than in
![]() ${\mathbf {\Gamma }}$
(see Example 4.15 below), which justifies the extra work that will be done below.
${\mathbf {\Gamma }}$
(see Example 4.15 below), which justifies the extra work that will be done below.
4.1 The o-minimal site on
 ${\mathbf {\Gamma }_{\infty } }$
-definable sets
${\mathbf {\Gamma }_{\infty } }$
-definable sets
Here we introduce the natural first-order logic structure
![]() ${\mathbf {\Gamma }_{\infty } }$
induced by
${\mathbf {\Gamma }_{\infty } }$
induced by
![]() ${\mathbf {\Gamma }}$
on
${\mathbf {\Gamma }}$
on
![]() ${\Gamma _{\infty } }$
and show that
${\Gamma _{\infty } }$
and show that
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable sets are equipped with a site making them
${\mathbf {\Gamma }_{\infty } }$
-definable sets are equipped with a site making them
![]() ${\mathcal {T}}$
-spaces.
${\mathcal {T}}$
-spaces.
For
![]() $x=(x_1, \ldots , x_m)\in {\Gamma ^m_{\infty } },$
the support of x, denoted
$x=(x_1, \ldots , x_m)\in {\Gamma ^m_{\infty } },$
the support of x, denoted
![]() $\mathrm {supp}\, x,$
is defined by
$\mathrm {supp}\, x,$
is defined by
For
![]() $L\subseteq \{1,\ldots , m\}$
, let
$L\subseteq \{1,\ldots , m\}$
, let
Then
![]() ${\Gamma ^m_{\infty } }=\bigsqcup _{L\subseteq \{1,\ldots , m\}}({\Gamma ^m_{\infty } } )_{L}$
,
${\Gamma ^m_{\infty } }=\bigsqcup _{L\subseteq \{1,\ldots , m\}}({\Gamma ^m_{\infty } } )_{L}$
,
![]() $({\Gamma ^m_{\infty } } )_{\{1,\ldots , m\}}={\Gamma ^m}$
and, if
$({\Gamma ^m_{\infty } } )_{\{1,\ldots , m\}}={\Gamma ^m}$
and, if
![]() $\tau _{L}\colon {\Gamma ^m_{\infty } }\to {\Gamma ^{|L|}_{\infty } }$
is the projection onto the
$\tau _{L}\colon {\Gamma ^m_{\infty } }\to {\Gamma ^{|L|}_{\infty } }$
is the projection onto the
![]() $|L|$
coordinates in
$|L|$
coordinates in
![]() $L,$
then the restriction
$L,$
then the restriction
![]() $\tau _{L|}\colon ({\Gamma ^m_{\infty } })_{L}\to {\Gamma ^{|L|}}$
is a bijection and
$\tau _{L|}\colon ({\Gamma ^m_{\infty } })_{L}\to {\Gamma ^{|L|}}$
is a bijection and
![]() $\tau _{\{1,\ldots ,m\} |}\colon {\Gamma ^m} \to {\Gamma ^m}$
is the identity.
$\tau _{\{1,\ldots ,m\} |}\colon {\Gamma ^m} \to {\Gamma ^m}$
is the identity.
If
![]() $\pi \colon {\Gamma ^m_{\infty } } \to {\Gamma ^k_{\infty } }$
is the projection onto the first k coordinates,
$\pi \colon {\Gamma ^m_{\infty } } \to {\Gamma ^k_{\infty } }$
is the projection onto the first k coordinates,
![]() $\pi '\colon {\Gamma ^m_{\infty } } \to \Gamma ^{m-k}_{\infty }$
is the projection onto the last
$\pi '\colon {\Gamma ^m_{\infty } } \to \Gamma ^{m-k}_{\infty }$
is the projection onto the last
![]() $m-k$
coordinates, and for
$m-k$
coordinates, and for
![]() $L\subseteq \{1,\ldots , m\}$
,
$L\subseteq \{1,\ldots , m\}$
,
![]() $\pi (L)=\{1,\ldots , k\}\cap L$
and
$\pi (L)=\{1,\ldots , k\}\cap L$
and
![]() $\pi '(L)=-k+\{k+1,\ldots , m\}\cap L,$
then
$\pi '(L)=-k+\{k+1,\ldots , m\}\cap L,$
then
-
(*)
 $$\begin{align*}\mathrm{supp} \,x=\mathrm{supp} \, \pi (x)\sqcup (k+\mathrm{supp} \, \pi'(x))\end{align*}$$
$$\begin{align*}\mathrm{supp} \,x=\mathrm{supp} \, \pi (x)\sqcup (k+\mathrm{supp} \, \pi'(x))\end{align*}$$
-
and moreover,
where
 $\pi ^L_k$
is a projection onto the first
$\pi ^L_k$
is a projection onto the first
 $\# \pi (L)$
coordinates and are commutative diagrams.
$\# \pi (L)$
coordinates and are commutative diagrams.
If, for
![]() $X\subseteq {\Gamma ^m_{\infty } }$
and for
$X\subseteq {\Gamma ^m_{\infty } }$
and for
![]() $L\subseteq \{1,\ldots , m\}$
, we set
$L\subseteq \{1,\ldots , m\}$
, we set
then
![]() $X=\bigsqcup _{L\subseteq \{1,\ldots , m\}}X_{L}$
and
$X=\bigsqcup _{L\subseteq \{1,\ldots , m\}}X_{L}$
and
![]() $X_{\{1,\ldots , m\}}=X\cap \Gamma ^m$
. Furthermore, the restriction
$X_{\{1,\ldots , m\}}=X\cap \Gamma ^m$
. Furthermore, the restriction
![]() $\tau _{L|}\colon X_{L}\to \tau _{L}(X_{L})$
is a bijection,
$\tau _{L|}\colon X_{L}\to \tau _{L}(X_{L})$
is a bijection,
![]() $\tau _L(X_L)\subseteq {\Gamma } ^{|L|}$
and
$\tau _L(X_L)\subseteq {\Gamma } ^{|L|}$
and
![]() $\tau _{\{1,\ldots ,m\} |}\colon X\cap {\Gamma ^m}\to X\cap {\Gamma ^m}$
is the identity.
$\tau _{\{1,\ldots ,m\} |}\colon X\cap {\Gamma ^m}\to X\cap {\Gamma ^m}$
is the identity.
For each m, let
Recall that an o-minimal structure (possibly with end points) has definable Skolem functions if, given a definable family
![]() $\{Y_t\}_{t\in T}$
, there is a definable function
$\{Y_t\}_{t\in T}$
, there is a definable function
![]() $f\colon T\to \bigcup _{t\in T} Y_t$
such that
$f\colon T\to \bigcup _{t\in T} Y_t$
such that
![]() $f(t)\in Y_t$
for each
$f(t)\in Y_t$
for each
![]() $t\in T$
. By the (observations before the) proof of [Reference van den Dries53, Chapter 6, (1.2)] (see also Comment (1.3) there), the o-minimal structure has definable Skolem functions if and only if every nonempty definable set X has a definable element
$t\in T$
. By the (observations before the) proof of [Reference van den Dries53, Chapter 6, (1.2)] (see also Comment (1.3) there), the o-minimal structure has definable Skolem functions if and only if every nonempty definable set X has a definable element
![]() $e(X)\in X$
.
$e(X)\in X$
.
The following Proposition is left to the reader.
Proposition 4.1.
![]() ${\mathbf {\Gamma }_{\infty } } =({\Gamma _{\infty } }, (\mathfrak {G}_m)_{m \in {\mathbb N}})$
is an o-minimal structure with right end point
${\mathbf {\Gamma }_{\infty } } =({\Gamma _{\infty } }, (\mathfrak {G}_m)_{m \in {\mathbb N}})$
is an o-minimal structure with right end point
![]() $\infty $
. Moreover, if
$\infty $
. Moreover, if
![]() ${\mathbf {\Gamma }}$
has definable Skolem functions, then
${\mathbf {\Gamma }}$
has definable Skolem functions, then
![]() ${\mathbf {\Gamma }_{\infty } }$
has definable Skolem functions.
${\mathbf {\Gamma }_{\infty } }$
has definable Skolem functions.
![]() $\Box $
$\Box $
Results in o-minimality usually are stated and proved for o-minimal structures without end points. Nearly all of those results can be checked to hold with exactly the same proof when there is an end point. Nevertheless, for convenience, we will now introduce a new structure without end points that contains as a substructure a copy of
![]() ${\mathbf {\Gamma }_{\infty } }$
.
${\mathbf {\Gamma }_{\infty } }$
.
Let
![]() ${\Sigma }=\{0\}\times {\Gamma _{\infty } } \cup \{1\}\times {\Gamma }$
be equipped with the natural order extending
${\Sigma }=\{0\}\times {\Gamma _{\infty } } \cup \{1\}\times {\Gamma }$
be equipped with the natural order extending
![]() $<$
on
$<$
on
![]() ${\Gamma }$
and on
${\Gamma }$
and on
![]() ${\Gamma _{\infty } }$
such that
${\Gamma _{\infty } }$
such that
![]() $(0,x) < (1,y)$
for all
$(0,x) < (1,y)$
for all
![]() $x\in {\Gamma _{\infty } }$
and all
$x\in {\Gamma _{\infty } }$
and all
![]() $y\in {\Gamma }$
.
$y\in {\Gamma }$
.
Set
![]() ${\Sigma } _0=\{0\}\times {\Gamma _{\infty } }$
,
${\Sigma } _0=\{0\}\times {\Gamma _{\infty } }$
,
![]() ${\Sigma } _1=\{1\}\times {\Gamma }$
and, for
${\Sigma } _1=\{1\}\times {\Gamma }$
and, for
![]() $\alpha \in 2^m,$
which below we identify with a sequence of 0s and 1s of length
$\alpha \in 2^m,$
which below we identify with a sequence of 0s and 1s of length
![]() $m$
, let
$m$
, let
Then
![]() ${\Sigma ^m}=\bigsqcup _{\alpha \in 2^m}{\Sigma } _{\alpha }$
,
${\Sigma ^m}=\bigsqcup _{\alpha \in 2^m}{\Sigma } _{\alpha }$
,
![]() ${\Sigma } _{\overline {0}}={\Sigma } _0^m$
and
${\Sigma } _{\overline {0}}={\Sigma } _0^m$
and
![]() ${\Sigma } _{\overline {1}}={\Sigma } _1^m$
. If
${\Sigma } _{\overline {1}}={\Sigma } _1^m$
. If
is the natural projection, then the restriction
![]() $\sigma _{m|}\colon {\Sigma } _{\alpha }\to {\Gamma ^m_{\infty } }$
is injective,
$\sigma _{m|}\colon {\Sigma } _{\alpha }\to {\Gamma ^m_{\infty } }$
is injective,
![]() $\sigma _{m|}\colon {\Sigma } _{\overline {0}}\to {\Gamma ^m_{\infty } }$
is a bijection with inverse the natural inclusion
$\sigma _{m|}\colon {\Sigma } _{\overline {0}}\to {\Gamma ^m_{\infty } }$
is a bijection with inverse the natural inclusion
![]() $\iota _m\colon {\Gamma ^m_{\infty } } \to {\Sigma } _0^m\colon (x_1,\ldots , x_m)\mapsto ((0,x_1), \ldots , (0,x_m))$
, and
$\iota _m\colon {\Gamma ^m_{\infty } } \to {\Sigma } _0^m\colon (x_1,\ldots , x_m)\mapsto ((0,x_1), \ldots , (0,x_m))$
, and
![]() $\sigma _{m|}\colon {\Sigma } _{\overline {1}}\to {\Gamma ^m}$
is a bijection with inverse the natural inclusion
$\sigma _{m|}\colon {\Sigma } _{\overline {1}}\to {\Gamma ^m}$
is a bijection with inverse the natural inclusion
![]() $\iota _m\colon {\Gamma ^m} \to {\Sigma } _1^m\colon (x_1,\ldots , x_m)\mapsto ((1,x_1), \ldots , (1,x_m))$
$\iota _m\colon {\Gamma ^m} \to {\Sigma } _1^m\colon (x_1,\ldots , x_m)\mapsto ((1,x_1), \ldots , (1,x_m))$
If
![]() $\pi \colon {\Sigma ^m} \to {\Sigma ^k}$
is the projection onto the first k pairs of coordinates,
$\pi \colon {\Sigma ^m} \to {\Sigma ^k}$
is the projection onto the first k pairs of coordinates,
![]() $\pi '\colon {\Sigma ^m} \to {\Sigma ^{m-k}}$
is the projection onto the last
$\pi '\colon {\Sigma ^m} \to {\Sigma ^{m-k}}$
is the projection onto the last
![]() $m-k$
pairs of coordinates, for
$m-k$
pairs of coordinates, for
![]() $\alpha \in 2^m, \ \pi (\alpha )\in 2^k$
is given by
$\alpha \in 2^m, \ \pi (\alpha )\in 2^k$
is given by
![]() $\pi (\alpha )=\alpha _{|\{1,\ldots , k\}}$
and
$\pi (\alpha )=\alpha _{|\{1,\ldots , k\}}$
and
![]() $\pi '(\alpha )\in 2^{m-k}$
is given by
$\pi '(\alpha )\in 2^{m-k}$
is given by
![]() $\pi '(\alpha )(s)=\alpha (s+k),$
then:
$\pi '(\alpha )(s)=\alpha (s+k),$
then:
-
(**)
where $$\begin{align*}\alpha =\pi (\alpha )* \pi'(\alpha ), \end{align*}$$
$$\begin{align*}\alpha =\pi (\alpha )* \pi'(\alpha ), \end{align*}$$
 $*$
is a concatenation of sequences, and moreover, and
$*$
is a concatenation of sequences, and moreover, and are commutative diagrams.
are commutative diagrams.
If, for
![]() $X\subseteq {\Sigma ^m}$
and for
$X\subseteq {\Sigma ^m}$
and for
![]() $\alpha \in 2^m$
, we set
$\alpha \in 2^m$
, we set
then
![]() $X=\bigsqcup _{\alpha \in 2^m}X_{\alpha }$
. Furthermore, the restriction
$X=\bigsqcup _{\alpha \in 2^m}X_{\alpha }$
. Furthermore, the restriction
![]() $\sigma _{m|}\colon X_{\alpha }\to \sigma _{m}(X_{\alpha })$
is a bijection,
$\sigma _{m|}\colon X_{\alpha }\to \sigma _{m}(X_{\alpha })$
is a bijection,
![]() $\sigma _m(X_{\alpha })\subseteq {\Gamma ^m_{\infty } }$
.
$\sigma _m(X_{\alpha })\subseteq {\Gamma ^m_{\infty } }$
.
For each m, let
Similarly to Proposition 4.1, we have:
Proposition 4.2.
![]() ${\mathbf {\Sigma }}=({\Sigma }, (\mathfrak {S}_m)_{m\in {\mathbb N}})$
is an o-minimal structure. Moreover, if
${\mathbf {\Sigma }}=({\Sigma }, (\mathfrak {S}_m)_{m\in {\mathbb N}})$
is an o-minimal structure. Moreover, if
![]() ${\mathbf {\Gamma }}$
has definable Skolem functions, then
${\mathbf {\Gamma }}$
has definable Skolem functions, then
![]() ${\mathbf {\Sigma }}$
has definable Skolem functions.
${\mathbf {\Sigma }}$
has definable Skolem functions.
![]() $\Box $
$\Box $
The following remarks are obvious from the constructions above:
Remark 4.3 (Natural embeddings).
We have:
-
(a) The structure
 ${\mathbf {\Gamma }}$
and the substructure
${\mathbf {\Gamma }}$
and the substructure
 $({\Gamma }, (\mathfrak {G}_m \cap {\Gamma ^m} )_{m\in {\mathbb N}})$
of
$({\Gamma }, (\mathfrak {G}_m \cap {\Gamma ^m} )_{m\in {\mathbb N}})$
of
 ${\mathbf {\Gamma }_{\infty } }$
have the same definable sets.
${\mathbf {\Gamma }_{\infty } }$
have the same definable sets. -
(b) Under the inclusion
 $\iota _1\colon {\Gamma _{\infty } }\to {\Sigma } _0,$
the structure
$\iota _1\colon {\Gamma _{\infty } }\to {\Sigma } _0,$
the structure
 ${\mathbf {\Gamma }_{\infty } }$
and the substructure
${\mathbf {\Gamma }_{\infty } }$
and the substructure
 $({\Sigma } _0, (\mathfrak {S}_m \cap {\Sigma } _0^m )_{m\in {\mathbb N}})$
of
$({\Sigma } _0, (\mathfrak {S}_m \cap {\Sigma } _0^m )_{m\in {\mathbb N}})$
of
 ${\mathbf {\Sigma }}$
have the same definable sets.
${\mathbf {\Sigma }}$
have the same definable sets.
So when convenient, below we will often identify
![]() ${\mathbf {\Gamma }_{\infty } }$
with its copy in
${\mathbf {\Gamma }_{\infty } }$
with its copy in
![]() ${\mathbf {\Sigma }}$
.
${\mathbf {\Sigma }}$
.
We now make a couple of observations comparing
![]() ${\mathbf {\Gamma }}$
,
${\mathbf {\Gamma }}$
,
![]() ${\mathbf {\Gamma }_{\infty } } $
and
${\mathbf {\Gamma }_{\infty } } $
and
![]() ${\mathbf {\Sigma }}$
.
${\mathbf {\Sigma }}$
.
Remark 4.4 (The topologies).
Let
![]() ${\mathbf {\Gamma }}=({\Gamma }, <,\ldots )$
be an arbitrary o-minimal structure without end points. Then the topology of
${\mathbf {\Gamma }}=({\Gamma }, <,\ldots )$
be an arbitrary o-minimal structure without end points. Then the topology of
![]() ${\Gamma }$
is generated by the open intervals
${\Gamma }$
is generated by the open intervals
![]() $(-\infty , a), (a,b)$
and
$(-\infty , a), (a,b)$
and
![]() $(b, \infty )$
with
$(b, \infty )$
with
![]() $a,b\in {\Gamma }$
and the topology of
$a,b\in {\Gamma }$
and the topology of
![]() ${\Gamma } ^n$
is generated by the products of n such open intervals.
${\Gamma } ^n$
is generated by the products of n such open intervals.
In
![]() ${\mathbf {\Gamma }_{\infty } }$
the topology of
${\mathbf {\Gamma }_{\infty } }$
the topology of
![]() ${\Gamma _{\infty } }$
is generated by the open intervals
${\Gamma _{\infty } }$
is generated by the open intervals
![]() $(-\infty , a), (a,b)$
and
$(-\infty , a), (a,b)$
and
![]() $(b, \infty ]$
with
$(b, \infty ]$
with
![]() $a,b\in {\Gamma }$
and the topology of
$a,b\in {\Gamma }$
and the topology of
![]() ${\Gamma ^n_{\infty } }$
is generated by the products of n such open intervals.
${\Gamma ^n_{\infty } }$
is generated by the products of n such open intervals.
It follows that:
-
•
 ${\Gamma ^m}$
is open in
${\Gamma ^m}$
is open in
 ${\Gamma ^m_{\infty } }$
, and the topology on
${\Gamma ^m_{\infty } }$
, and the topology on
 ${\Gamma ^m}$
is the induced topology from
${\Gamma ^m}$
is the induced topology from
 ${\Gamma ^m_{\infty } }$
.
${\Gamma ^m_{\infty } }$
. -
•
 ${\Gamma ^m_{\infty } }$
is closed in
${\Gamma ^m_{\infty } }$
is closed in
 ${\Sigma ^m}$
, and the topology on
${\Sigma ^m}$
, and the topology on
 ${\Gamma ^m_{\infty } }$
is the induced topology from
${\Gamma ^m_{\infty } }$
is the induced topology from
 ${\Sigma ^m}$
.
${\Sigma ^m}$
.
Recall the notion of cell in
![]() ${\Gamma ^n_{\infty } }$
defined inductively as follows:
${\Gamma ^n_{\infty } }$
defined inductively as follows:
-
• A cell in
 ${\Gamma _{\infty } }$
is either a singleton
${\Gamma _{\infty } }$
is either a singleton
 $\{a\}$
or
$\{a\}$
or
 $\{\infty \}$
or an open interval of the form
$\{\infty \}$
or an open interval of the form
 $(-\infty , a)$
or
$(-\infty , a)$
or
 $(a,b)$
for
$(a,b)$
for
 $a,b\in {\Gamma }$
with
$a,b\in {\Gamma }$
with
 $a<b$
.
$a<b$
. -
• A cell in
 $\Gamma ^{n+1}_{\infty }$
is a set of the form or
$\Gamma ^{n+1}_{\infty }$
is a set of the form or $$\begin{align*}\Gamma(h)=\{(x,y)\in \Gamma ^{n+1}_{\infty }: x\in X\,\,\textrm{and}\,\,y=h(x)\}, \end{align*}$$
or
$$\begin{align*}\Gamma(h)=\{(x,y)\in \Gamma ^{n+1}_{\infty }: x\in X\,\,\textrm{and}\,\,y=h(x)\}, \end{align*}$$
or $$\begin{align*}(f,g)_X=\{(x,y)\in \Gamma ^{n+1}_{\infty }: x\in X\,\,\textrm{and}\,\,f(x)<y<g(x)\}, \end{align*}$$
for some
$$\begin{align*}(f,g)_X=\{(x,y)\in \Gamma ^{n+1}_{\infty }: x\in X\,\,\textrm{and}\,\,f(x)<y<g(x)\}, \end{align*}$$
for some $$\begin{align*}(-\infty , g)_X=\{(x,y)\in \Gamma ^{n+1}_{\infty }: x\in X\,\,\textrm{and}\,\,y<g(x)\}, \end{align*}$$
$$\begin{align*}(-\infty , g)_X=\{(x,y)\in \Gamma ^{n+1}_{\infty }: x\in X\,\,\textrm{and}\,\,y<g(x)\}, \end{align*}$$
 ${\mathbf {\Gamma }_{\infty } }$
-definable and continuous maps
${\mathbf {\Gamma }_{\infty } }$
-definable and continuous maps
 $f, g,h\colon X\to {\Gamma _{\infty } }$
with
$f, g,h\colon X\to {\Gamma _{\infty } }$
with
 $f<g$
, where X is a cell in
$f<g$
, where X is a cell in
 ${\Gamma ^n_{\infty } }$
.
${\Gamma ^n_{\infty } }$
.
In either case, X is called the domain of the defined cell.
Remark 4.5 (Cell decompositions).
As in [Reference van den Dries53, Chapter 3, (2.11)] (the proof also works in the case with end points), we have:
-
• Given any
 ${\mathbf {\Gamma }_{\infty } }$
-definable sets
${\mathbf {\Gamma }_{\infty } }$
-definable sets
 $A_1, \dots , A_k\subseteq {\Gamma ^n_{\infty } }$
, there is a decomposition
$A_1, \dots , A_k\subseteq {\Gamma ^n_{\infty } }$
, there is a decomposition
 ${\mathcal {C}}$
of
${\mathcal {C}}$
of
 ${\Gamma ^n_{\infty } }$
that partitions each
${\Gamma ^n_{\infty } }$
that partitions each
 $A_i$
.
$A_i$
. -
• Given a
 ${\mathbf {\Gamma }_{\infty } }$
-definable map
${\mathbf {\Gamma }_{\infty } }$
-definable map
 $f\colon A\to {\Gamma _{\infty } }$
, there is a decomposition
$f\colon A\to {\Gamma _{\infty } }$
, there is a decomposition
 ${\mathcal {C}}$
of
${\mathcal {C}}$
of
 ${\Gamma ^n_{\infty } }$
that partitions A such that the restriction
${\Gamma ^n_{\infty } }$
that partitions A such that the restriction
 $f_{|B}$
to each
$f_{|B}$
to each
 $B\in {\mathcal {C}}$
with
$B\in {\mathcal {C}}$
with
 $B\subseteq A$
is continuous.
$B\subseteq A$
is continuous.
Here (see [Reference van den Dries53, Chapter 3, (2.10)]), a decomposition of
![]() ${\Gamma _{\infty } }$
is a partition of
${\Gamma _{\infty } }$
is a partition of
![]() ${\Gamma _{\infty } }$
into cells and a decomposition of
${\Gamma _{\infty } }$
into cells and a decomposition of
![]() $\Gamma ^{k+1}_{\infty }$
is a partition of
$\Gamma ^{k+1}_{\infty }$
is a partition of
![]() $\Gamma ^{k+1}_{\infty }$
into cells such that its projection to
$\Gamma ^{k+1}_{\infty }$
into cells such that its projection to
![]() ${\Gamma ^k_{\infty } }$
is a decomposition of
${\Gamma ^k_{\infty } }$
is a decomposition of
![]() ${\Gamma ^k_{\infty } }$
.
${\Gamma ^k_{\infty } }$
.
By the inductive construction of cells, it is easy to see that:
-
(a) If
 ${\mathcal {C}}$
is a cell decomposition of
${\mathcal {C}}$
is a cell decomposition of
 ${\Gamma ^m_{\infty } }$
, then (i)
${\Gamma ^m_{\infty } }$
, then (i)
 ${\mathcal {C}}$
partitions the sets in
${\mathcal {C}}$
partitions the sets in
 $\{({\Gamma ^m_{\infty } } )_L : L\subseteq \{1,\ldots , m\}\}$
; in particular,
$\{({\Gamma ^m_{\infty } } )_L : L\subseteq \{1,\ldots , m\}\}$
; in particular,
 ${\mathcal {C}} _{|{\Gamma ^m}}$
is a cell decomposition of
${\mathcal {C}} _{|{\Gamma ^m}}$
is a cell decomposition of
 ${\Gamma ^m}$
. (ii) The cells in
${\Gamma ^m}$
. (ii) The cells in
 ${\mathcal {C}}$
are built using
${\mathcal {C}}$
are built using
 ${\mathbf {\Gamma }_{\infty } }$
-definable continuous maps
${\mathbf {\Gamma }_{\infty } }$
-definable continuous maps
 $f\colon X\to {\Gamma _{\infty } }$
with
$f\colon X\to {\Gamma _{\infty } }$
with
 $X\subseteq ({\Gamma ^m_{\infty } })_L$
a cell and such that f is constant with value
$X\subseteq ({\Gamma ^m_{\infty } })_L$
a cell and such that f is constant with value
 $\infty $
or where
$\infty $
or where $$\begin{align*}f=f_L\circ\tau_L, \end{align*}$$
$$\begin{align*}f=f_L\circ\tau_L, \end{align*}$$
 $f_L\colon \tau _L(X)\to {\Gamma }$
is a
$f_L\colon \tau _L(X)\to {\Gamma }$
is a
 ${\mathbf {\Gamma }}$
-definable continuous map.
${\mathbf {\Gamma }}$
-definable continuous map.
-
(b) If
 ${\mathcal {B}}$
is a cell decomposition of
${\mathcal {B}}$
is a cell decomposition of
 ${\Sigma ^m}$
that partitions the sets in
${\Sigma ^m}$
that partitions the sets in
 $\{({\Gamma ^m_{\infty } } )_L : L\subseteq \{1,\ldots , m\}\}$
, then
$\{({\Gamma ^m_{\infty } } )_L : L\subseteq \{1,\ldots , m\}\}$
, then
 ${\mathcal {B}} _{|{\Gamma ^m_{\infty } }}$
is a cell decomposition of
${\mathcal {B}} _{|{\Gamma ^m_{\infty } }}$
is a cell decomposition of
 ${\Gamma ^m_{\infty } }$
.
${\Gamma ^m_{\infty } }$
.
In an arbitrary o-minimal structure, a definable set X is definably connected if and only if the only clopen definable subsets of X are
![]() $\emptyset $
and X. We say that a
$\emptyset $
and X. We say that a
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable subset of
${\mathbf {\Gamma }_{\infty } }$
-definable subset of
![]() ${\Gamma ^m_{\infty } }$
is
${\Gamma ^m_{\infty } }$
is
![]() ${\mathbf {\Gamma }_{\infty } }$
-definably locally closed if and only if it is the intersection of an open
${\mathbf {\Gamma }_{\infty } }$
-definably locally closed if and only if it is the intersection of an open
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable subset of
${\mathbf {\Gamma }_{\infty } }$
-definable subset of
![]() ${\Gamma ^m_{\infty } }$
and a closed
${\Gamma ^m_{\infty } }$
and a closed
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable subset of
${\mathbf {\Gamma }_{\infty } }$
-definable subset of
![]() ${\Gamma ^m_{\infty } }$
or equivalently if and only if it is open in its closure in
${\Gamma ^m_{\infty } }$
or equivalently if and only if it is open in its closure in
![]() ${\Gamma ^m_{\infty } }$
. A similar definition applies in
${\Gamma ^m_{\infty } }$
. A similar definition applies in
![]() ${\mathbf {\Gamma }}$
.
${\mathbf {\Gamma }}$
.
Remark 4.6 (Definable connectedness).
From the above remark about the topologies, a
![]() ${\mathbf {\Gamma }}$
-definable subset of
${\mathbf {\Gamma }}$
-definable subset of
![]() ${\Gamma ^m}$
is
${\Gamma ^m}$
is
![]() ${\mathbf {\Gamma }}$
-definably connected if and only if it is
${\mathbf {\Gamma }}$
-definably connected if and only if it is
![]() ${\mathbf {\Gamma }_{\infty } }$
-definably connected, and a
${\mathbf {\Gamma }_{\infty } }$
-definably connected, and a
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable subset of
${\mathbf {\Gamma }_{\infty } }$
-definable subset of
![]() ${\Gamma ^m_{\infty } }$
is
${\Gamma ^m_{\infty } }$
is
![]() ${\mathbf {\Gamma }_{\infty } }$
-definably connected if and only if it is
${\mathbf {\Gamma }_{\infty } }$
-definably connected if and only if it is
![]() ${\mathbf {\Sigma }}$
-definably connected. Hence, just like in
${\mathbf {\Sigma }}$
-definably connected. Hence, just like in
![]() ${\mathbf {\Gamma }},$
by [Reference van den Dries53, Chapter 3, Proposition 2.18]:
${\mathbf {\Gamma }},$
by [Reference van den Dries53, Chapter 3, Proposition 2.18]:
-
• Every
 ${\mathbf {\Gamma }_{\infty } }$
-definable subset of
${\mathbf {\Gamma }_{\infty } }$
-definable subset of
 ${\Gamma ^m_{\infty } }$
has finitely many
${\Gamma ^m_{\infty } }$
has finitely many
 ${\mathbf {\Gamma }_{\infty } }$
-definably connected components that are clopen and partition the
${\mathbf {\Gamma }_{\infty } }$
-definably connected components that are clopen and partition the
 ${\mathbf {\Gamma }_{\infty } }$
-definable set.
${\mathbf {\Gamma }_{\infty } }$
-definable set.
Remark 4.7 (Definably locally closed subsets).
Since cells in
![]() ${\Gamma ^m}$
are
${\Gamma ^m}$
are
![]() ${\mathbf {\Gamma }}$
-definably locally closed ([Reference van den Dries53, page 51]), by cell decomposition theorem, every
${\mathbf {\Gamma }}$
-definably locally closed ([Reference van den Dries53, page 51]), by cell decomposition theorem, every
![]() ${\mathbf {\Gamma }}$
-definable subset of
${\mathbf {\Gamma }}$
-definable subset of
![]() ${\Gamma ^m}$
is a finite union of
${\Gamma ^m}$
is a finite union of
![]() ${\mathbf {\Gamma }}$
-definably locally closed sets. Working in
${\mathbf {\Gamma }}$
-definably locally closed sets. Working in
![]() ${\mathbf {\Sigma }}$
, it follows, by Remark 4.4, that:
${\mathbf {\Sigma }}$
, it follows, by Remark 4.4, that:
-
• Every
 ${\mathbf {\Gamma }_{\infty } }$
-definable subset of
${\mathbf {\Gamma }_{\infty } }$
-definable subset of
 ${\Gamma ^m_{\infty } }$
is a finite union of
${\Gamma ^m_{\infty } }$
is a finite union of
 ${\mathbf {\Gamma }_{\infty } }$
-definably locally closed sets.
${\mathbf {\Gamma }_{\infty } }$
-definably locally closed sets.
Just like in
![]() ${\mathbf {\Gamma }},$
if
${\mathbf {\Gamma }},$
if
![]() $({\Gamma },<)$
is nonarchimedean as a linear order, then infinite
$({\Gamma },<)$
is nonarchimedean as a linear order, then infinite
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable spaces with the topology generated by open definable subsets are in general totally disconnected and not locally compact. So, as in Example 3.7 (3), to develop cohomology, one studies
${\mathbf {\Gamma }_{\infty } }$
-definable spaces with the topology generated by open definable subsets are in general totally disconnected and not locally compact. So, as in Example 3.7 (3), to develop cohomology, one studies
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable spaces X equipped with the o-minimal site:
${\mathbf {\Gamma }_{\infty } }$
-definable spaces X equipped with the o-minimal site:
Definition 4.8 (O-minimal site on
 ${\mathbf {\Gamma }_{\infty } }$
-definable subsets).
${\mathbf {\Gamma }_{\infty } }$
-definable subsets).
Let
![]() ${\mathbf {\Gamma }}= ({\Gamma },<, \ldots )$
be an arbitrary o-minimal structure without end points. If X is a
${\mathbf {\Gamma }}= ({\Gamma },<, \ldots )$
be an arbitrary o-minimal structure without end points. If X is a
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable subset of
${\mathbf {\Gamma }_{\infty } }$
-definable subset of
![]() ${\Gamma ^m_{\infty } },$
then the o-minimal site
${\Gamma ^m_{\infty } },$
then the o-minimal site
![]() $X_{\mathrm {def}}$
on X is the category
$X_{\mathrm {def}}$
on X is the category
![]() $\mathrm {Op} (X_{\mathrm {def}})$
whose objects are open (in the topology of X mentioned above)
$\mathrm {Op} (X_{\mathrm {def}})$
whose objects are open (in the topology of X mentioned above)
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable subsets of X, the morphisms are the inclusions, and the admissible covers
${\mathbf {\Gamma }_{\infty } }$
-definable subsets of X, the morphisms are the inclusions, and the admissible covers
![]() $\mathrm {Cov} (U)$
of
$\mathrm {Cov} (U)$
of
![]() $U\in \mathrm {Op} (X_{\mathrm {def}})$
are covers by open
$U\in \mathrm {Op} (X_{\mathrm {def}})$
are covers by open
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable subsets of X with finite subcovers.
${\mathbf {\Gamma }_{\infty } }$
-definable subsets of X with finite subcovers.
Proposition 4.9. Let
![]() ${\mathbf {\Gamma }}= ({\Gamma },<, \ldots )$
be an arbitrary o-minimal structure without end points. If X is a
${\mathbf {\Gamma }}= ({\Gamma },<, \ldots )$
be an arbitrary o-minimal structure without end points. If X is a
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable subset of
${\mathbf {\Gamma }_{\infty } }$
-definable subset of
![]() ${\Gamma ^m_{\infty } }$
, let
${\Gamma ^m_{\infty } }$
, let
Then X is a
![]() ${\mathcal {T}}$
-space,
${\mathcal {T}}$
-space,
![]() $X_{{\mathcal {T}}}=X_{\mathrm {def}}$
, and
$X_{{\mathcal {T}}}=X_{\mathrm {def}}$
, and
![]() $\widetilde {X}_{{\mathcal {T}}}$
is the o-minimal spectrum
$\widetilde {X}_{{\mathcal {T}}}$
is the o-minimal spectrum
![]() $\widetilde {X}$
of X: that is, its points are types over
$\widetilde {X}$
of X: that is, its points are types over
![]() ${\Gamma _{\infty } }$
concentrated on X. Furthermore, there is an equivalence of categories
${\Gamma _{\infty } }$
concentrated on X. Furthermore, there is an equivalence of categories
Proof. By Remark 4.4,
![]() ${\mathcal {T}}$
is a basis for a topology of
${\mathcal {T}}$
is a basis for a topology of
![]() $X,$
and
$X,$
and
![]() $\emptyset \in {\mathcal {T}};$
it is clear that
$\emptyset \in {\mathcal {T}};$
it is clear that
![]() ${\mathcal {T}}$
is closed under finite unions and intersections; by Remark 4.7, the
${\mathcal {T}}$
is closed under finite unions and intersections; by Remark 4.7, the
![]() ${\mathcal {T}}$
-subsets of X are exactly the
${\mathcal {T}}$
-subsets of X are exactly the
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable subsets of X. Therefore, from Remark 4.6, it follows that every
${\mathbf {\Gamma }_{\infty } }$
-definable subsets of X. Therefore, from Remark 4.6, it follows that every
![]() $U\in {\mathcal {T}}$
has finitely many
$U\in {\mathcal {T}}$
has finitely many
![]() ${\mathcal {T}}$
-connected components. The rest follows from the definitions and results in Subsection 3.1.
${\mathcal {T}}$
-connected components. The rest follows from the definitions and results in Subsection 3.1.
The following remark will allow us to work in
![]() ${\mathbf {\Gamma }_{\infty } }$
instead of
${\mathbf {\Gamma }_{\infty } }$
instead of
![]() ${\mathbf {\Gamma }}$
or in
${\mathbf {\Gamma }}$
or in
![]() ${\mathbf {\Sigma }}$
instead of in
${\mathbf {\Sigma }}$
instead of in
![]() ${\mathbf {\Gamma }_{\infty } }$
when convenient:
${\mathbf {\Gamma }_{\infty } }$
when convenient:
Remark 4.10. Let
![]() ${\mathbf {\Gamma }} =({\Gamma }, <,\ldots )$
be an arbitrary o-minimal structure without end points. By Remark 4.4, we have:
${\mathbf {\Gamma }} =({\Gamma }, <,\ldots )$
be an arbitrary o-minimal structure without end points. By Remark 4.4, we have:
-
• If
 $X\subseteq {\Gamma ^m}$
is a
$X\subseteq {\Gamma ^m}$
is a
 ${\mathbf {\Gamma }}$
-definable subset, then the o-minimal site of X in
${\mathbf {\Gamma }}$
-definable subset, then the o-minimal site of X in
 ${\mathbf {\Gamma }}$
is the same as the o-minimal site of X in
${\mathbf {\Gamma }}$
is the same as the o-minimal site of X in
 ${\mathbf {\Gamma }_{\infty } }$
, so the o-minimal sheaf and cohomology theories of X in
${\mathbf {\Gamma }_{\infty } }$
, so the o-minimal sheaf and cohomology theories of X in
 ${\mathbf {\Gamma }}$
are the same as the o-minimal sheaf and cohomology theories of X in
${\mathbf {\Gamma }}$
are the same as the o-minimal sheaf and cohomology theories of X in
 ${\mathbf {\Gamma }_{\infty } }$
.
${\mathbf {\Gamma }_{\infty } }$
. -
• If
 $X\subseteq {\Gamma ^m_{\infty } }$
is a
$X\subseteq {\Gamma ^m_{\infty } }$
is a
 ${\mathbf {\Gamma }_{\infty } }$
-definable subset, then the o-minimal site of X in
${\mathbf {\Gamma }_{\infty } }$
-definable subset, then the o-minimal site of X in
 ${\mathbf {\Gamma }_{\infty } }$
is the same as the o-minimal site of X in
${\mathbf {\Gamma }_{\infty } }$
is the same as the o-minimal site of X in
 ${\mathbf {\Sigma }}$
, so the o-minimal sheaf and cohomology theories of X in
${\mathbf {\Sigma }}$
, so the o-minimal sheaf and cohomology theories of X in
 ${\mathbf {\Gamma }_{\infty } }$
are the same as the o-minimal sheaf and cohomology theories of X in
${\mathbf {\Gamma }_{\infty } }$
are the same as the o-minimal sheaf and cohomology theories of X in
 ${\mathbf {\Sigma }}$
.
${\mathbf {\Sigma }}$
.
4.2 Definable compactness and definable normality
In this subsection, we recall the notion of definable compactness for definable sets in
![]() ${\mathbf {\Gamma }_{\infty } }$
(defined in analogy to the case
${\mathbf {\Gamma }_{\infty } }$
(defined in analogy to the case
![]() ${\mathbf {\Gamma }}$
) and make a couple of remarks about locally definably compact and definable completions that will be used later. We introduce the notion of definable normality (which corresponds to
${\mathbf {\Gamma }}$
) and make a couple of remarks about locally definably compact and definable completions that will be used later. We introduce the notion of definable normality (which corresponds to
![]() ${\mathcal {T}}$
-normality for the associated
${\mathcal {T}}$
-normality for the associated
![]() ${\mathcal {T}}$
-topology) and prove that when
${\mathcal {T}}$
-topology) and prove that when
![]() ${\mathbf {\Gamma }}$
is an o-minimal expansion of an ordered group, every definably locally closed subset of
${\mathbf {\Gamma }}$
is an o-minimal expansion of an ordered group, every definably locally closed subset of
![]() ${\Gamma ^n_{\infty } }$
is the union of finitely many open definable subsets that are definably normal (Theorem 4.28).
${\Gamma ^n_{\infty } }$
is the union of finitely many open definable subsets that are definably normal (Theorem 4.28).
As in [Reference Peterzil and Steinhorn45], we say that a
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable subset
${\mathbf {\Gamma }_{\infty } }$
-definable subset
![]() $X\subseteq {\Gamma ^m_{\infty } }$
is
$X\subseteq {\Gamma ^m_{\infty } }$
is
![]() ${\mathbf {\Gamma }_{\infty } }$
-definably compact if and only if for every
${\mathbf {\Gamma }_{\infty } }$
-definably compact if and only if for every
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable and continuous map from an open interval in
${\mathbf {\Gamma }_{\infty } }$
-definable and continuous map from an open interval in
![]() ${\Gamma _{\infty } }$
into X, the limits at the end points of the interval exist in X. Recall that X is locally
${\Gamma _{\infty } }$
into X, the limits at the end points of the interval exist in X. Recall that X is locally
![]() ${\mathbf {\Gamma }_{\infty } }$
-definably compact if and only if every point in X has a
${\mathbf {\Gamma }_{\infty } }$
-definably compact if and only if every point in X has a
![]() ${\mathbf {\Gamma }_{\infty } }$
-definably compact neighbourhood.
${\mathbf {\Gamma }_{\infty } }$
-definably compact neighbourhood.
Remark 4.11 (Definable compactness).
Note that in the above definition it is enough to consider open intervals of the form
![]() $(-\infty ,a), (a,b)$
or
$(-\infty ,a), (a,b)$
or
![]() $(b, \infty )$
, where
$(b, \infty )$
, where
![]() $a,b \in {\Gamma }$
and
$a,b \in {\Gamma }$
and
![]() $a<b$
. Therefore:
$a<b$
. Therefore:
-
• A
 ${\mathbf {\Gamma }}$
-definable subset
${\mathbf {\Gamma }}$
-definable subset
 $X\subseteq {\Gamma ^m}$
is
$X\subseteq {\Gamma ^m}$
is
 ${\mathbf {\Gamma }}$
-definably compact if and only if it is
${\mathbf {\Gamma }}$
-definably compact if and only if it is
 ${\mathbf {\Gamma }_{\infty } }$
-definably compact.
${\mathbf {\Gamma }_{\infty } }$
-definably compact.
On the other hand, since for any interval I in
![]() ${\Sigma }={\Sigma } _0\sqcup {\Sigma } _1$
, we have that
${\Sigma }={\Sigma } _0\sqcup {\Sigma } _1$
, we have that
![]() $I\cap {\Sigma } _0$
and
$I\cap {\Sigma } _0$
and
![]() $I\cap {\Sigma } _1,$
if non-empty, are intervals in
$I\cap {\Sigma } _1,$
if non-empty, are intervals in
![]() ${\Gamma _{\infty } },$
it follows that:
${\Gamma _{\infty } },$
it follows that:
-
• A
 ${\mathbf {\Gamma }_{\infty } }$
-definable subset
${\mathbf {\Gamma }_{\infty } }$
-definable subset
 $X\subseteq {\Gamma ^m_{\infty } }$
is
$X\subseteq {\Gamma ^m_{\infty } }$
is
 ${\mathbf {\Gamma }_{\infty } }$
-definably compact if and only if it is
${\mathbf {\Gamma }_{\infty } }$
-definably compact if and only if it is
 ${\Sigma }$
-definably compact.
${\Sigma }$
-definably compact.
In particular, by [Reference Peterzil and Steinhorn45, Theorem 2.1], we have:
-
• A
 ${\mathbf {\Gamma }_{\infty } }$
-definable subset
${\mathbf {\Gamma }_{\infty } }$
-definable subset
 $X\subseteq {\Gamma ^m_{\infty } }$
is
$X\subseteq {\Gamma ^m_{\infty } }$
is
 ${\mathbf {\Gamma }_{\infty } }$
-definably compact if and only if it is closed and bounded in
${\mathbf {\Gamma }_{\infty } }$
-definably compact if and only if it is closed and bounded in
 ${\Gamma ^m_{\infty } }$
: that is,
${\Gamma ^m_{\infty } }$
: that is,
 $X\subseteq \Pi _{i=1}^m[c_i, \infty ]$
for some
$X\subseteq \Pi _{i=1}^m[c_i, \infty ]$
for some
 $c_i\in \Gamma $
(
$c_i\in \Gamma $
(
 $i=1,\ldots , m$
).
$i=1,\ldots , m$
).
Recall that a type
![]() $\beta $
on X (i.e., an ultrafilter of definable subsets of X) is a definable type on X if and only if for every uniformly definable family
$\beta $
on X (i.e., an ultrafilter of definable subsets of X) is a definable type on X if and only if for every uniformly definable family
![]() $\{Y_t\}_{t\in T}$
of definable subsets of
$\{Y_t\}_{t\in T}$
of definable subsets of
![]() $X,$
the set
$X,$
the set
![]() $\{t\in T: Y_t\in \beta \}$
is a definable set. And we say a definable type
$\{t\in T: Y_t\in \beta \}$
is a definable set. And we say a definable type
![]() $\beta $
on X has limit
$\beta $
on X has limit
![]() $a \in X$
if for any definable neighbourhood
$a \in X$
if for any definable neighbourhood
![]() $a\in U$
, we have
$a\in U$
, we have
![]() $\beta $
concentrates on U. It is worth pointing out that the definition in [Reference Hrushovski and Loeser35] of definable compactness of X is that any definable type on X has a limit in X. At first glance, this seems to be a stronger criterion than defined above. However, both of them turn out to be the same as being closed and bounded. The main advantage of the definable type definition is that one cannot use a definable path on X to describe the topological closure of X, yet the set of limits of definable types on X is the topological closure of X. This failure is also noted in [Reference Peterzil and Steinhorn45, Theorem 2.3]. Nonetheless, this does not affect the characterisation of definable compactness in
$\beta $
concentrates on U. It is worth pointing out that the definition in [Reference Hrushovski and Loeser35] of definable compactness of X is that any definable type on X has a limit in X. At first glance, this seems to be a stronger criterion than defined above. However, both of them turn out to be the same as being closed and bounded. The main advantage of the definable type definition is that one cannot use a definable path on X to describe the topological closure of X, yet the set of limits of definable types on X is the topological closure of X. This failure is also noted in [Reference Peterzil and Steinhorn45, Theorem 2.3]. Nonetheless, this does not affect the characterisation of definable compactness in
![]() ${\mathbf {\Gamma }_{\infty } }$
.
${\mathbf {\Gamma }_{\infty } }$
.
Remark 4.12 (Locally definably compact).
As in topology, locally definably compact is equivalent to definably locally closed. Suppose that X is locally definably compact. Let
![]() $a\in X$
and K be a definably compact definable neighbourhood of a in X. Let U be an open definable neighbourhood of a such that
$a\in X$
and K be a definably compact definable neighbourhood of a in X. Let U be an open definable neighbourhood of a such that
![]() $U\cap X\subseteq K$
. Taking closures in
$U\cap X\subseteq K$
. Taking closures in
![]() $\overline {X}$
and noting that
$\overline {X}$
and noting that
![]() $\overline {U\cap \overline {X}}=\overline {U\cap X}$
, we obtain
$\overline {U\cap \overline {X}}=\overline {U\cap X}$
, we obtain
which shows that X is open in
![]() $\overline {X}$
. The other implication is also easy.
$\overline {X}$
. The other implication is also easy.
Remark 4.13 (Definable completions).
Let
![]() $X\subseteq {\Gamma ^m_{\infty } }$
be a
$X\subseteq {\Gamma ^m_{\infty } }$
be a
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable set that is bounded in
${\mathbf {\Gamma }_{\infty } }$
-definable set that is bounded in
![]() ${\mathbf {\Gamma }_{\infty } }$
and is locally
${\mathbf {\Gamma }_{\infty } }$
and is locally
![]() ${\mathbf {\Gamma }_{\infty } }$
-definably compact. Then the inclusion
${\mathbf {\Gamma }_{\infty } }$
-definably compact. Then the inclusion
![]() $i\colon X\hookrightarrow \overline {X}$
into the closure of X in
$i\colon X\hookrightarrow \overline {X}$
into the closure of X in
![]() ${\Gamma ^m_{\infty } }$
is a
${\Gamma ^m_{\infty } }$
is a
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable completion of X: that is,
${\mathbf {\Gamma }_{\infty } }$
-definable completion of X: that is,
-
(i)
 $\overline {X}$
is
$\overline {X}$
is
 ${\mathbf {\Gamma }_{\infty } }$
-definably compact.
${\mathbf {\Gamma }_{\infty } }$
-definably compact. -
(ii)
 $i\colon X\hookrightarrow \overline {X}$
is a
$i\colon X\hookrightarrow \overline {X}$
is a
 ${\mathbf {\Gamma }_{\infty } }$
-definable open immersion (i.e.,
${\mathbf {\Gamma }_{\infty } }$
-definable open immersion (i.e.,
 $i(X)$
is open in
$i(X)$
is open in
 $\overline {X}$
and
$\overline {X}$
and
 $i\colon X\to i(X)$
is a
$i\colon X\to i(X)$
is a
 ${\mathbf {\Gamma }_{\infty } }$
-definable homeomorphism).
${\mathbf {\Gamma }_{\infty } }$
-definable homeomorphism). -
(iii) The image
 $i(X)$
is dense in
$i(X)$
is dense in
 $\overline {X}$
.
$\overline {X}$
.
Everything here is clear, and
![]() $i(X)$
is open in
$i(X)$
is open in
![]() $\overline {X}$
by Remark 4.12.
$\overline {X}$
by Remark 4.12.
It follows that:
-
• If
 ${\mathbf {\Gamma }}=({\Gamma }, <, +, \ldots )$
is an o-minimal expansion of an ordered group
${\mathbf {\Gamma }}=({\Gamma }, <, +, \ldots )$
is an o-minimal expansion of an ordered group
 $({\Gamma } , <, + ),$
then every
$({\Gamma } , <, + ),$
then every
 ${\mathbf {\Gamma }_{\infty } }$
-definably locally closed subset of
${\mathbf {\Gamma }_{\infty } }$
-definably locally closed subset of
 ${\Gamma ^m_{\infty } }$
is
${\Gamma ^m_{\infty } }$
is
 ${\mathbf {\Gamma }_{\infty } }$
-definably completable.
${\mathbf {\Gamma }_{\infty } }$
-definably completable.
Indeed, let
![]() $p\colon {\Gamma _{\infty } } \to {\Gamma _{\infty } } \times {\Gamma _{\infty } }$
be the
$p\colon {\Gamma _{\infty } } \to {\Gamma _{\infty } } \times {\Gamma _{\infty } }$
be the
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable map given by
${\mathbf {\Gamma }_{\infty } }$
-definable map given by
 $$ \begin{align*} p(x)= \begin{cases} (-x,0) \qquad \textrm{if} \,\,x<0\\ \\ (0,x) \qquad \,\,\,\, \textrm{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} p(x)= \begin{cases} (-x,0) \qquad \textrm{if} \,\,x<0\\ \\ (0,x) \qquad \,\,\,\, \textrm{otherwise.} \end{cases} \end{align*} $$
Then
![]() $p({\Gamma _{\infty } } )\subseteq [0,\infty ]\times [0,\infty ]$
and
$p({\Gamma _{\infty } } )\subseteq [0,\infty ]\times [0,\infty ]$
and
![]() $p\colon {\Gamma _{\infty } }\to p({\Gamma _{\infty } })$
is a
$p\colon {\Gamma _{\infty } }\to p({\Gamma _{\infty } })$
is a
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable homeomorphism. So every
${\mathbf {\Gamma }_{\infty } }$
-definable homeomorphism. So every
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable subset of
${\mathbf {\Gamma }_{\infty } }$
-definable subset of
![]() ${\Gamma ^m_{\infty } }$
is
${\Gamma ^m_{\infty } }$
is
![]() ${\mathbf {\Gamma }_{\infty } }$
-definably homeomorphic to a
${\mathbf {\Gamma }_{\infty } }$
-definably homeomorphic to a
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable subset of
${\mathbf {\Gamma }_{\infty } }$
-definable subset of
![]() $[0,\infty ]^{2m}$
(which is in particular bounded in
$[0,\infty ]^{2m}$
(which is in particular bounded in
![]() ${\mathbf {\Gamma }_{\infty } }$
).
${\mathbf {\Gamma }_{\infty } }$
).
However, note that
![]() ${\mathbf {\Gamma }}$
-definable completions do not exist in general for locally
${\mathbf {\Gamma }}$
-definable completions do not exist in general for locally
![]() ${\mathbf {\Gamma }}$
-definably compact spaces. Suppose that
${\mathbf {\Gamma }}$
-definably compact spaces. Suppose that
![]() ${\mathbf {\Gamma }}=({\Gamma }, <, +, \ldots )$
is a semi-bounded o-minimal expansion of an ordered group
${\mathbf {\Gamma }}=({\Gamma }, <, +, \ldots )$
is a semi-bounded o-minimal expansion of an ordered group
![]() $({\Gamma } , <, +)$
(see [Reference Edmundo21, Definition 1.5]). Let
$({\Gamma } , <, +)$
(see [Reference Edmundo21, Definition 1.5]). Let
![]() $X={\Gamma }$
, and suppose that there is a
$X={\Gamma }$
, and suppose that there is a
![]() ${\mathbf {\Gamma }}$
-definable completion
${\mathbf {\Gamma }}$
-definable completion
![]() $\iota \colon X\hookrightarrow P$
of X. Since P is
$\iota \colon X\hookrightarrow P$
of X. Since P is
![]() ${\mathbf {\Gamma }}$
-definably compact, the limit
${\mathbf {\Gamma }}$
-definably compact, the limit
![]() $\lim _{t\to +\infty }\iota (t)$
exists in P: call it a. Let
$\lim _{t\to +\infty }\iota (t)$
exists in P: call it a. Let
![]() $(P_i, \theta _i)$
be a
$(P_i, \theta _i)$
be a
![]() ${\mathbf {\Gamma }}$
-definable chart of P such that
${\mathbf {\Gamma }}$
-definable chart of P such that
![]() $a\in P_i$
. Let
$a\in P_i$
. Let
![]() $\Pi _{j=1}^{n_i}(c_j^-, c_j^+)$
be an open and bounded box in
$\Pi _{j=1}^{n_i}(c_j^-, c_j^+)$
be an open and bounded box in
![]() $\Gamma ^{n_i}$
containing
$\Gamma ^{n_i}$
containing
![]() $\theta _i(a)$
. By continuity, there exists
$\theta _i(a)$
. By continuity, there exists
![]() $b\in {\Gamma }$
be such that
$b\in {\Gamma }$
be such that
![]() $\theta _i\circ \iota ((b, +\infty ))\subseteq \Pi _{j=1}^{n_i}(c_j^-, c_j^+)$
. Hence,
$\theta _i\circ \iota ((b, +\infty ))\subseteq \Pi _{j=1}^{n_i}(c_j^-, c_j^+)$
. Hence,
![]() $\theta _i\circ \iota _{|}\colon (b, +\infty )\to \Gamma ^{n_i}$
has bounded image; so, by [Reference Edmundo21, Fact 1.6 and Proposition 3.1 (1)], this map must be eventually constant. This contradicts the fact that the map is injective.
$\theta _i\circ \iota _{|}\colon (b, +\infty )\to \Gamma ^{n_i}$
has bounded image; so, by [Reference Edmundo21, Fact 1.6 and Proposition 3.1 (1)], this map must be eventually constant. This contradicts the fact that the map is injective.
Recall that, in an arbitrary o-minimal structure, a definable subset X with the induced topology is definably normal if and only if every two disjoint closed definable subsets of X can be separated by disjoint open definable subsets of X. This corresponds to X being
![]() ${\mathcal {T}}$
-normal (Definition 3.11) for the
${\mathcal {T}}$
-normal (Definition 3.11) for the
![]() ${\mathcal {T}}$
-topology given by the o-minimal site on X.
${\mathcal {T}}$
-topology given by the o-minimal site on X.
Remark 4.14 (Definable normality).
By Remark 4.4, definable normality of a definable set does not change when moving between
![]() ${\mathbf {\Gamma }}$
,
${\mathbf {\Gamma }}$
,
![]() ${\mathbf {\Gamma }_{\infty } }$
and
${\mathbf {\Gamma }_{\infty } }$
and
![]() ${\mathbf {\Sigma }}$
. Therefore, by Remark 4.11 and [Reference Edmundo, Mamino and Prelli23, Theorem 2.11], we have:
${\mathbf {\Sigma }}$
. Therefore, by Remark 4.11 and [Reference Edmundo, Mamino and Prelli23, Theorem 2.11], we have:
-
• If
 ${\mathbf {\Gamma }}$
has definable Skolem functions, then every
${\mathbf {\Gamma }}$
has definable Skolem functions, then every
 ${\mathbf {\Gamma }_{\infty } }$
-definably compact set is
${\mathbf {\Gamma }_{\infty } }$
-definably compact set is
 ${\mathbf {\Gamma }_{\infty } }$
-definably normal.
${\mathbf {\Gamma }_{\infty } }$
-definably normal.
On the other hand, if
![]() ${\mathbf {\Gamma }}=({\Gamma }, <, +, \ldots )$
is an o-minimal expansion of an ordered group
${\mathbf {\Gamma }}=({\Gamma }, <, +, \ldots )$
is an o-minimal expansion of an ordered group
![]() $({\Gamma } , <, + ),$
then by [Reference van den Dries53, Chapter 6 (3.5)], every
$({\Gamma } , <, + ),$
then by [Reference van den Dries53, Chapter 6 (3.5)], every
![]() ${\mathbf {\Gamma }}$
-definable set is
${\mathbf {\Gamma }}$
-definable set is
![]() ${\mathbf {\Gamma }}$
-definably normal. However, this is not true in
${\mathbf {\Gamma }}$
-definably normal. However, this is not true in
![]() ${\mathbf {\Gamma }_{\infty } }$
(and so it is also not true in
${\mathbf {\Gamma }_{\infty } }$
(and so it is also not true in
![]() ${\mathbf {\Sigma }}$
), as shown in the following example.
${\mathbf {\Sigma }}$
), as shown in the following example.
Example 4.15. Let
![]() $a\in {\Gamma }$
, and let
$a\in {\Gamma }$
, and let
![]() $U=\Gamma ^2_{\infty }\setminus \{(\infty , a)\}$
. Let
$U=\Gamma ^2_{\infty }\setminus \{(\infty , a)\}$
. Let
![]() $C=\ {\Gamma } \times \{a\}$
, and let
$C=\ {\Gamma } \times \{a\}$
, and let
![]() $D=\{\infty \}\times ({\Gamma _{\infty } } \setminus \{a\})$
. Then U is an open
$D=\{\infty \}\times ({\Gamma _{\infty } } \setminus \{a\})$
. Then U is an open
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable subset of
${\mathbf {\Gamma }_{\infty } }$
-definable subset of
![]() $\Gamma ^2_{\infty }$
and C and D are closed and disjoint
$\Gamma ^2_{\infty }$
and C and D are closed and disjoint
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable subsets of U. We claim that there are no disjoint open
${\mathbf {\Gamma }_{\infty } }$
-definable subsets of U. We claim that there are no disjoint open
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable subsets V and W of U such that
${\mathbf {\Gamma }_{\infty } }$
-definable subsets V and W of U such that
![]() $C\subseteq V$
and
$C\subseteq V$
and
![]() $D\subseteq W$
.
$D\subseteq W$
.
For a contradiction, suppose that such V and W exist. Let
![]() $b\in {\Gamma }$
be such that
$b\in {\Gamma }$
be such that
![]() $b<a$
. Let
$b<a$
. Let
![]() $f\colon \Gamma \to [b, a)$
be the
$f\colon \Gamma \to [b, a)$
be the
![]() ${\mathbf {\Gamma }}$
-definable function given by
${\mathbf {\Gamma }}$
-definable function given by
![]() $f(t)=\inf \{x\in (b, a): \{t\}\times (x, a)\,\, \subseteq V\cap {\Gamma } ^2\}$
. By [Reference Edmundo21, Fact 1.6 and Proposition 3.1 (1)], there is
$f(t)=\inf \{x\in (b, a): \{t\}\times (x, a)\,\, \subseteq V\cap {\Gamma } ^2\}$
. By [Reference Edmundo21, Fact 1.6 and Proposition 3.1 (1)], there is
![]() $s\in {\Gamma }$
and
$s\in {\Gamma }$
and
![]() $c\in [b,a)$
such that
$c\in [b,a)$
such that
![]() $f_{|\,(s,\infty )}$
is constant and equal to c. So
$f_{|\,(s,\infty )}$
is constant and equal to c. So
![]() $(s,\infty )\times (c,a) \,\, \subseteq V$
. Let
$(s,\infty )\times (c,a) \,\, \subseteq V$
. Let
![]() $(\infty , u)\in \{\infty \}\times (c,a) \,\, \subseteq D$
be any point. Since W is an open
$(\infty , u)\in \{\infty \}\times (c,a) \,\, \subseteq D$
be any point. Since W is an open
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable neighbourhood of D in U, it is an open
${\mathbf {\Gamma }_{\infty } }$
-definable neighbourhood of D in U, it is an open
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable neighbourhood of
${\mathbf {\Gamma }_{\infty } }$
-definable neighbourhood of
![]() $(\infty ,u)$
in U. So there are
$(\infty ,u)$
in U. So there are
![]() $c<u_1<u<u_2<a$
and
$c<u_1<u<u_2<a$
and
![]() $v<\infty $
such that
$v<\infty $
such that
![]() $(v,\infty ]\times (u_1,u_2)\,\, \subseteq W$
. Let
$(v,\infty ]\times (u_1,u_2)\,\, \subseteq W$
. Let
![]() $w=\max \{s,v\}$
. Then
$w=\max \{s,v\}$
. Then
![]() $(w,\infty )\times (u_1,u_2) \,\, \subseteq V\cap W,$
contradicting the fact that V and W are disjoint.
$(w,\infty )\times (u_1,u_2) \,\, \subseteq V\cap W,$
contradicting the fact that V and W are disjoint.
Let us now recall the following result from [Reference Edmundo and Prelli28] that will be true in
![]() ${\mathbf {\Gamma }_{\infty } }$
by working in
${\mathbf {\Gamma }_{\infty } }$
by working in
![]() ${\mathbf {\Sigma }}$
. After a couple of lemmas, we will prove a result (Theorem 4.22 below) generalising this fact.
${\mathbf {\Sigma }}$
. After a couple of lemmas, we will prove a result (Theorem 4.22 below) generalising this fact.
Fact 4.16 [Reference Edmundo and Prelli28, Theorem 2.20].
Let Z and K be definable spaces in an o-minimal structure with definable Skolem functions with Z definably normal and K Hausdorff and definably compact. Then
![]() $Z\times K$
is definably normal.
$Z\times K$
is definably normal.
![]() $\Box $
$\Box $
So from now on, let
![]() ${\mathbf M} =(M, <, \ldots )$
be an arbitrary o-minimal structure without end points and with definable Skolem functions.
${\mathbf M} =(M, <, \ldots )$
be an arbitrary o-minimal structure without end points and with definable Skolem functions.
Lemma 4.17. If
![]() $I\subseteq M$
is an interval, then I is definably normal. In particular, every open definable subset of M has a finite cover by open, definable subsets that are definably normal.Footnote
2
$I\subseteq M$
is an interval, then I is definably normal. In particular, every open definable subset of M has a finite cover by open, definable subsets that are definably normal.Footnote
2
Proof. Let C and D be disjoint, closed, definable subsets of I. Then C is a finite union of intervals. The result follows by induction on the number of such intervals. Suppose that C is an interval. Let c be the left end point of C and
![]() $c'$
the right end point. Let
$c'$
the right end point. Let
![]() $d=\sup \{x\in D:x<c\}$
, and let
$d=\sup \{x\in D:x<c\}$
, and let
![]() $d'=\inf \{x\in D:c'<x\}$
. Since C and D are closed in I and disjoint, we have
$d'=\inf \{x\in D:c'<x\}$
. Since C and D are closed in I and disjoint, we have
![]() $d<c\leq c'<d'$
. Now take
$d<c\leq c'<d'$
. Now take
![]() $d<u<v<c$
and
$d<u<v<c$
and
![]() $c'<v'<u'<d'$
. Then
$c'<v'<u'<d'$
. Then
![]() $U=((-\infty , u)\cup (u',\infty ))\cap I$
and
$U=((-\infty , u)\cup (u',\infty ))\cap I$
and
![]() $V=(v,v')$
are disjoint, open, definable subsets of I such that
$V=(v,v')$
are disjoint, open, definable subsets of I such that
![]() $D\subseteq U$
and
$D\subseteq U$
and
![]() $C\subseteq V$
.
$C\subseteq V$
.
If C is a union of
![]() $n+1$
intervals, let
$n+1$
intervals, let
![]() $C'$
be the union of the leftmost n intervals, and let
$C'$
be the union of the leftmost n intervals, and let
![]() $C"$
be the rightmost interval. By induction, there are open definable subsets
$C"$
be the rightmost interval. By induction, there are open definable subsets
![]() $U', V'$
and
$U', V'$
and
![]() $U", V"$
of I such that
$U", V"$
of I such that
![]() $D\subseteq U'$
,
$D\subseteq U'$
,
![]() $C'\subseteq V'$
,
$C'\subseteq V'$
,
![]() $D\subseteq U", \ C"\subseteq V"$
,
$D\subseteq U", \ C"\subseteq V"$
,
![]() $U'\cap V'=\emptyset $
and
$U'\cap V'=\emptyset $
and
![]() $U"\cap V"=\emptyset $
. Let
$U"\cap V"=\emptyset $
. Let
![]() $U=U'\cap U"$
and
$U=U'\cap U"$
and
![]() $V=V'\cup V"$
. Then U and V are disjoint, open, definable subsets of I such that
$V=V'\cup V"$
. Then U and V are disjoint, open, definable subsets of I such that
![]() $D\subseteq U$
and
$D\subseteq U$
and
![]() $C\subseteq V$
.
$C\subseteq V$
.
Below, we use the following notation: for each
![]() $i\in \{1, \ldots , m\}$
, let
$i\in \{1, \ldots , m\}$
, let
be the projection omitting the ith coordinate, and let
be the projection onto the ith coordinate. If
![]() $Z\subseteq M^{m-1}$
is a definable subset and
$Z\subseteq M^{m-1}$
is a definable subset and
![]() $f, g\colon Z\to M$
are continuous definable maps with
$f, g\colon Z\to M$
are continuous definable maps with
![]() $f<g$
, then for each
$f<g$
, then for each
![]() $i\in \{1,\ldots , m\},$
we let
$i\in \{1,\ldots , m\},$
we let
and we define
in a similar way.
Lemma 4.18. The restriction
is a continuous, closed, definable map.
Proof. For
![]() $z\in Z$
, let
$z\in Z$
, let
and for
![]() $d\in D(z)$
, let
$d\in D(z)$
, let
Then
![]() $\{U(z,d)\}_{d\in D(z)}$
is a uniformly definable system of fundamental open neighbourhoods of z in Z. Moreover, since the relation
$\{U(z,d)\}_{d\in D(z)}$
is a uniformly definable system of fundamental open neighbourhoods of z in Z. Moreover, since the relation
![]() $d\preceq d'$
on
$d\preceq d'$
on
![]() $D(z)$
given by
$D(z)$
given by
![]() $U(z,d)\subseteq U(z,d')$
is a definable downwards directed order on
$U(z,d)\subseteq U(z,d')$
is a definable downwards directed order on
![]() $D(z),$
by [Reference Hrushovski and Loeser35, Lemma 4.2.18] (or [Reference Hrushovski34, Lemma 2.19]), there is a definable type
$D(z),$
by [Reference Hrushovski and Loeser35, Lemma 4.2.18] (or [Reference Hrushovski34, Lemma 2.19]), there is a definable type
![]() $\beta $
on
$\beta $
on
![]() $D(z)$
such that for every
$D(z)$
such that for every
![]() $d\in D(z)$
, we have
$d\in D(z)$
, we have
![]() $\{d' \in D(z): d'\preceq d\}\in \beta $
.
$\{d' \in D(z): d'\preceq d\}\in \beta $
.
Let
![]() $S\subseteq [f, g]^i _Z$
be a closed definable subset. Suppose that
$S\subseteq [f, g]^i _Z$
be a closed definable subset. Suppose that
![]() $\pi _i(S)$
is not closed in Z. Then there is
$\pi _i(S)$
is not closed in Z. Then there is
![]() $z\in Z\setminus \pi _i(S)$
such that for all
$z\in Z\setminus \pi _i(S)$
such that for all
![]() $d\in D(z)$
, we have
$d\in D(z)$
, we have
![]() $U(z,d)\cap \pi _i(S)\neq \emptyset $
. Then by definable Skolem functions, there is a definable map
$U(z,d)\cap \pi _i(S)\neq \emptyset $
. Then by definable Skolem functions, there is a definable map
such that for every
![]() $d\in D(z)$
, we have
$d\in D(z)$
, we have
![]() $\pi _i(h(d))\in U(z,d)\cap \pi _i(S)$
.
$\pi _i(h(d))\in U(z,d)\cap \pi _i(S)$
.
Let
![]() $\alpha $
be the definable type on S determined by the collection
$\alpha $
be the definable type on S determined by the collection
![]() $\{A\subseteq S: h^{-1}(A)\in \beta \}$
. Let
$\{A\subseteq S: h^{-1}(A)\in \beta \}$
. Let
![]() $\alpha _1$
be the definable type on
$\alpha _1$
be the definable type on
![]() $\pi _i(S)$
determined by the collection
$\pi _i(S)$
determined by the collection
![]() $\{A\subseteq \pi _i(S): (\pi _i)^{-1}(A)\in \alpha \}$
, and let
$\{A\subseteq \pi _i(S): (\pi _i)^{-1}(A)\in \alpha \}$
, and let
![]() $\alpha _2$
be the definable type on M determined by the collection
$\alpha _2$
be the definable type on M determined by the collection
![]() $\{A\subseteq M: (\pi ^{\prime }_i)^{-1}(A)\in \alpha \}$
.
$\{A\subseteq M: (\pi ^{\prime }_i)^{-1}(A)\in \alpha \}$
.
Claim 4.19. The limit of
![]() $\alpha $
exists, it is of the form
$\alpha $
exists, it is of the form
![]() $(z,c)$
and belongs to
$(z,c)$
and belongs to
![]() $[f,g]^i_Z$
.
$[f,g]^i_Z$
.
Proof. We have that z is the limit of
![]() $\alpha _1$
: that is, for every open definable subset V of Z such that
$\alpha _1$
: that is, for every open definable subset V of Z such that
![]() $z\in V$
, we have
$z\in V$
, we have
![]() $V\in \alpha _1$
. Indeed, given any such V, there is
$V\in \alpha _1$
. Indeed, given any such V, there is
![]() $d'$
such that
$d'$
such that
![]() $U(z,d')\subseteq V$
and
$U(z,d')\subseteq V$
and
 $$ \begin{align*} h^{-1}((\pi _i)^{-1}(V))&\supseteq h^{-1}((\pi _i)^{-1}(\pi _i(S)\cap U(z,d')))\\ &\supseteq h^{-1}((S\cap (\pi _i)^{-1}(U(z,d'))))\\ &\supseteq \{d"\in D(z):d"\preceq d'\}. \end{align*} $$
$$ \begin{align*} h^{-1}((\pi _i)^{-1}(V))&\supseteq h^{-1}((\pi _i)^{-1}(\pi _i(S)\cap U(z,d')))\\ &\supseteq h^{-1}((S\cap (\pi _i)^{-1}(U(z,d'))))\\ &\supseteq \{d"\in D(z):d"\preceq d'\}. \end{align*} $$
Since
![]() $[f,g]^i_Z\in \alpha $
, it follows that for every open definable subset V of Z such that
$[f,g]^i_Z\in \alpha $
, it follows that for every open definable subset V of Z such that
![]() $z\in V$
, we have
$z\in V$
, we have
![]() $[f,g]^i_V=(\pi _i)^{-1}(V)\cap [f, g]^i_Z\in \alpha $
. On the other hand, since
$[f,g]^i_V=(\pi _i)^{-1}(V)\cap [f, g]^i_Z\in \alpha $
. On the other hand, since
![]() $\alpha _2$
is a definable type on
$\alpha _2$
is a definable type on
![]() $M,$
by [Reference Marker and Steinhorn41, Lemma 2.3],
$M,$
by [Reference Marker and Steinhorn41, Lemma 2.3],
![]() $\alpha _2$
is not a cut, so
$\alpha _2$
is not a cut, so
![]() $\alpha _2$
is determined by either (i)
$\alpha _2$
is determined by either (i)
![]() $\{b<x: b\in M\}$
, (ii)
$\{b<x: b\in M\}$
, (ii)
![]() $x=a$
, (iii)
$x=a$
, (iii)
![]() $\{b<x<a: b\in M, \,\,b<a\}$
, (iv)
$\{b<x<a: b\in M, \,\,b<a\}$
, (iv)
![]() $\{a<x<b: b\in M, \,\,a<b\}$
or (v)
$\{a<x<b: b\in M, \,\,a<b\}$
or (v)
![]() $\{x<b:b\in M\}$
, where
$\{x<b:b\in M\}$
, where
![]() $a\in M$
. In case (i), the limit of
$a\in M$
. In case (i), the limit of
![]() $\alpha _2$
is
$\alpha _2$
is
![]() $+\infty $
; in cases (ii), (iii) and (iv), a is the limit of
$+\infty $
; in cases (ii), (iii) and (iv), a is the limit of
![]() $\alpha _2$
; and in case (v),
$\alpha _2$
; and in case (v),
![]() $-\infty $
is the limit of
$-\infty $
is the limit of
![]() $\alpha _2$
. Let c be the limit of
$\alpha _2$
. Let c be the limit of
![]() $\alpha _2$
.
$\alpha _2$
.
We show that
![]() $f(z)\leq c\leq g(z)$
. If
$f(z)\leq c\leq g(z)$
. If
![]() $g(z)< c$
, let l be such that
$g(z)< c$
, let l be such that
![]() $g(z)<l<c$
. Then since g is continuous, there is an open definable subset V of Z such that
$g(z)<l<c$
. Then since g is continuous, there is an open definable subset V of Z such that
![]() $z\in V$
and
$z\in V$
and
![]() $g(v)<l$
for all
$g(v)<l$
for all
![]() $v\in V$
. Case (v) does not occur since we cannot have
$v\in V$
. Case (v) does not occur since we cannot have
![]() $g(z)<-\infty ;$
in the remaining cases, we would have
$g(z)<-\infty ;$
in the remaining cases, we would have
![]() $\emptyset =[f,g]^i_V \cap (\pi ^{\prime }_i)^{-1}((l, +\infty )) \in \alpha $
, which is absurd. If
$\emptyset =[f,g]^i_V \cap (\pi ^{\prime }_i)^{-1}((l, +\infty )) \in \alpha $
, which is absurd. If
![]() $c<f(z)$
let l be such that
$c<f(z)$
let l be such that
![]() $c<l<f(z)$
. Then since f is continuous, there is an open definable subset V of Z such that
$c<l<f(z)$
. Then since f is continuous, there is an open definable subset V of Z such that
![]() $z\in V$
and
$z\in V$
and
![]() $c<l<f(v)$
for all
$c<l<f(v)$
for all
![]() $v\in V$
. Case (i) does not happen; in the remaining cases, we would have
$v\in V$
. Case (i) does not happen; in the remaining cases, we would have
![]() $\emptyset =[f,g]^i_V \cap (\pi ^{\prime }_i)^{-1} ((-\infty , l)) \in \alpha $
, which is absurd.
$\emptyset =[f,g]^i_V \cap (\pi ^{\prime }_i)^{-1} ((-\infty , l)) \in \alpha $
, which is absurd.
It follows that
![]() $(z,c)\in [f,g]^i _Z$
is the limit of
$(z,c)\in [f,g]^i _Z$
is the limit of
![]() $\alpha $
. Since S is closed in
$\alpha $
. Since S is closed in
![]() $[f, g]^i _Z$
and
$[f, g]^i _Z$
and
![]() $\alpha $
is a definable type on
$\alpha $
is a definable type on
![]() $S,$
its limit
$S,$
its limit
![]() $(z,c)$
is in S. But then
$(z,c)$
is in S. But then
![]() $z\in \pi _i(S)$
, which is a contradiction.
$z\in \pi _i(S)$
, which is a contradiction.
The previous result allows us to obtain a slight generalisation of [Reference Edmundo and Prelli28, Lemma 2.23]. In that Lemma, instead of
![]() $[f,g]^i _Z$
, we have
$[f,g]^i _Z$
, we have
![]() $Z\times [a,b]$
. The proof of this new version is exactly the same using Lemma 4.18 instead of the fact that the projection
$Z\times [a,b]$
. The proof of this new version is exactly the same using Lemma 4.18 instead of the fact that the projection
![]() $\pi \colon Z\times [a,b]\to Z$
is a continuous, closed definable map. For the reader’s convenience, we include the details.
$\pi \colon Z\times [a,b]\to Z$
is a continuous, closed definable map. For the reader’s convenience, we include the details.
Lemma 4.20. Let
![]() $Z\subseteq M^{m-1}$
be a definably normal definable subset. Let
$Z\subseteq M^{m-1}$
be a definably normal definable subset. Let
![]() $S\subseteq [f,g]^i_Z$
be a closed definable subset and
$S\subseteq [f,g]^i_Z$
be a closed definable subset and
![]() $W\subseteq [f,g]^i_Z$
an open definable subset. Then for every closed definable subset
$W\subseteq [f,g]^i_Z$
an open definable subset. Then for every closed definable subset
![]() $F\subseteq \pi _i(S)$
such that
$F\subseteq \pi _i(S)$
such that
![]() $S\cap (\pi _i)^{-1}(F)\subseteq W$
, there is an open definable neighbourhood O of F in Z such that
$S\cap (\pi _i)^{-1}(F)\subseteq W$
, there is an open definable neighbourhood O of F in Z such that
![]() $O\subseteq \overline {O}\cap Z\subseteq \pi _i(W)$
and
$O\subseteq \overline {O}\cap Z\subseteq \pi _i(W)$
and
![]() $S\cap (\pi _i)^{-1}(\overline {O}\cap Z)\subseteq W$
.
$S\cap (\pi _i)^{-1}(\overline {O}\cap Z)\subseteq W$
.
Proof. Let
![]() $W^c=([f,g]^i_Z)\setminus W$
. If
$W^c=([f,g]^i_Z)\setminus W$
. If
![]() $S\subseteq W$
, then since
$S\subseteq W$
, then since
![]() $\pi _i(S) \subseteq \pi _i(W)$
is closed in Z (by Lemma 4.18) and Z is definably normal, there is an open definable neighbourhood O of
$\pi _i(S) \subseteq \pi _i(W)$
is closed in Z (by Lemma 4.18) and Z is definably normal, there is an open definable neighbourhood O of
![]() $\pi _i(S)\supseteq F$
in Z such that
$\pi _i(S)\supseteq F$
in Z such that
![]() $O\subseteq \overline {O}\cap Z\subseteq \pi _i(W)$
, so
$O\subseteq \overline {O}\cap Z\subseteq \pi _i(W)$
, so
![]() $S\cap (\pi _i)^{-1}(\overline {O}\cap Z)=S\subseteq W$
. So we may suppose that
$S\cap (\pi _i)^{-1}(\overline {O}\cap Z)=S\subseteq W$
. So we may suppose that
![]() $S\cap W^c\neq \emptyset $
.
$S\cap W^c\neq \emptyset $
.
For
![]() $z\in Z$
, let
$z\in Z$
, let
![]() $\{U(z,d)\}_{d\in D(z)}$
be the uniformly definable system of fundamental open neighbourhoods of z in Z given above. Recall that by [Reference Hrushovski and Loeser35, Lemma 4.2.18] (or [Reference Hrushovski34, Lemma 2.19]), there is a definable type
$\{U(z,d)\}_{d\in D(z)}$
be the uniformly definable system of fundamental open neighbourhoods of z in Z given above. Recall that by [Reference Hrushovski and Loeser35, Lemma 4.2.18] (or [Reference Hrushovski34, Lemma 2.19]), there is a definable type
![]() $\beta $
on
$\beta $
on
![]() $D(z)$
such that for every
$D(z)$
such that for every
![]() $d\in D(z)$
, we have
$d\in D(z)$
, we have
![]() $\{d' \in D(z): d'\preceq d\}\in \beta $
.
$\{d' \in D(z): d'\preceq d\}\in \beta $
.
Suppose that
![]() $z\in F$
and for all
$z\in F$
and for all
![]() $d\in D(z),$
we have
$d\in D(z),$
we have
![]() $(S\cap (\pi _i)^{-1}(U(z,d)))\cap W^c\neq \emptyset $
. Then by definable Skolem functions, there is a definable map
$(S\cap (\pi _i)^{-1}(U(z,d)))\cap W^c\neq \emptyset $
. Then by definable Skolem functions, there is a definable map
such that for every
![]() $d\in D(z)$
, we have
$d\in D(z)$
, we have
![]() $h(d)\in (S\cap (\pi _i)^{-1}(U(z,d)))\cap W^c$
.
$h(d)\in (S\cap (\pi _i)^{-1}(U(z,d)))\cap W^c$
.
Let
![]() $\alpha $
be the definable type on
$\alpha $
be the definable type on
![]() $S\cap W^c$
determined by the collection
$S\cap W^c$
determined by the collection
![]() $\{A\subseteq S\cap W^c: h^{-1}(A)\in \beta \}$
. We are in the setup of Claim 4.19, so the limit of
$\{A\subseteq S\cap W^c: h^{-1}(A)\in \beta \}$
. We are in the setup of Claim 4.19, so the limit of
![]() $\alpha $
exists; it is of the form
$\alpha $
exists; it is of the form
![]() $(z,c)\in [f,g]^i_Z$
. Since
$(z,c)\in [f,g]^i_Z$
. Since
![]() $S\cap W^c$
is closed and
$S\cap W^c$
is closed and
![]() $\alpha $
is a definable type on
$\alpha $
is a definable type on
![]() $S\cap W^c$
, its limit
$S\cap W^c$
, its limit
![]() $(z,c)$
is in
$(z,c)$
is in
![]() $S\cap W^c$
. But then
$S\cap W^c$
. But then
![]() $(z,c)\in S\cap (\pi _i)^{-1}(z)\subseteq W^c$
, which contradicts the assumption on F.
$(z,c)\in S\cap (\pi _i)^{-1}(z)\subseteq W^c$
, which contradicts the assumption on F.
So for each
![]() $z\in F$
, there is
$z\in F$
, there is
![]() $d\in D(z)$
such that
$d\in D(z)$
such that
![]() $S\cap (\pi _i)^{-1}(U(z,d))\subseteq W$
. By definable Skolem functions, there is a definable map
$S\cap (\pi _i)^{-1}(U(z,d))\subseteq W$
. By definable Skolem functions, there is a definable map
![]() $\epsilon \colon F\to M^{2(m-1)}$
such that for each
$\epsilon \colon F\to M^{2(m-1)}$
such that for each
![]() $z\in F$
, we have
$z\in F$
, we have
![]() $\epsilon (z)\in D(z)$
and
$\epsilon (z)\in D(z)$
and
![]() $S\cap (\pi _i)^{-1}(U(z,\epsilon (z)))\subseteq W$
. Then
$S\cap (\pi _i)^{-1}(U(z,\epsilon (z)))\subseteq W$
. Then
is an open definable neighbourhood of F in Z such that
Since
![]() $U(F,\epsilon )\cap \pi _i(W)$
is an open definable neighbourhood of F in
$U(F,\epsilon )\cap \pi _i(W)$
is an open definable neighbourhood of F in
![]() $Z, \ F$
is closed in Z and Z is definably normal, there is an open definable neighbourhood O of F in Z such that
$Z, \ F$
is closed in Z and Z is definably normal, there is an open definable neighbourhood O of F in Z such that
![]() $O\subseteq \overline {O}\cap Z\subseteq U(F,\epsilon )\cap \pi _i(W)\subseteq \pi _i(W)$
and
$O\subseteq \overline {O}\cap Z\subseteq U(F,\epsilon )\cap \pi _i(W)\subseteq \pi _i(W)$
and
![]() $S\cap (\pi _i)^{-1}(\overline {O}\cap Z)\subseteq W$
.
$S\cap (\pi _i)^{-1}(\overline {O}\cap Z)\subseteq W$
.
We now obtain the following generalisation of the fact that if
![]() $Z\subseteq M^{m-1}$
is definably normal, then
$Z\subseteq M^{m-1}$
is definably normal, then
![]() $Z\times [a,b]$
is definably normal. We omit the proof since it is exactly the same as in [Reference Edmundo and Prelli28, Lemma 2.24, proof of Proposition 2.21] using Lemma 4.20 and basic o-minimality from [Reference van den Dries53].
$Z\times [a,b]$
is definably normal. We omit the proof since it is exactly the same as in [Reference Edmundo and Prelli28, Lemma 2.24, proof of Proposition 2.21] using Lemma 4.20 and basic o-minimality from [Reference van den Dries53].
Proposition 4.21. If
![]() $Z\subseteq M^{m-1}$
is definably normal, then
$Z\subseteq M^{m-1}$
is definably normal, then
![]() $[f,g]^i_Z$
is also definably normal.
$[f,g]^i_Z$
is also definably normal.
![]() $\Box $
$\Box $
We now extend this result a bit further. First we introduce some notation. Given
![]() $I\subseteq \{1,\ldots , m\},$
we let
$I\subseteq \{1,\ldots , m\},$
we let
![]() $I'=\{1,\ldots ,m\}\setminus I,$
we let
$I'=\{1,\ldots ,m\}\setminus I,$
we let
be the projection omitting the coordinates in I, and we let
be the projection onto the coordinates in I (so
![]() $\pi ^{\prime }_I=\pi _{I'}$
). Given
$\pi ^{\prime }_I=\pi _{I'}$
). Given
![]() $Z\subseteq M ^{|I|}$
a definable set and families
$Z\subseteq M ^{|I|}$
a definable set and families
![]() $\{f^l\colon Z\to M\}_{l\in I'}$
and
$\{f^l\colon Z\to M\}_{l\in I'}$
and
![]() $\{g^l\colon Z\to M\}_{l\in I'}$
of continuous definable functions, we set
$\{g^l\colon Z\to M\}_{l\in I'}$
of continuous definable functions, we set
Similarly, we define
If
![]() $g^l=g$
for all
$g^l=g$
for all
![]() $l\in I'$
, we write
$l\in I'$
, we write
instead and similarly for the case
![]() $f^l=f$
for all
$f^l=f$
for all
![]() $l\in I'$
(although we will not need this other case).
$l\in I'$
(although we will not need this other case).
Note that if
![]() $I=\{1,\ldots , m\},$
then
$I=\{1,\ldots , m\},$
then
Theorem 4.22. If
![]() $Z\subseteq M^{|I|}$
is definably normal, then
$Z\subseteq M^{|I|}$
is definably normal, then
![]() $[\{f^l\}_{l\in I'},\{g^l\}_{l\in I'}]^I_Z$
is also definably normal.
$[\{f^l\}_{l\in I'},\{g^l\}_{l\in I'}]^I_Z$
is also definably normal.
Proof. The proof is by induction on m. The case
![]() $m=0$
is clear, so assume
$m=0$
is clear, so assume
![]() $m>0$
and the result holds for
$m>0$
and the result holds for
![]() $m-1$
. If
$m-1$
. If
![]() $|I'|=0,$
then
$|I'|=0,$
then
![]() $I=\{1,\ldots , m\}$
, so
$I=\{1,\ldots , m\}$
, so
![]() $[\{f^l\}_{l\in I'}, \{g^l\}_{l\in I'}]^I_Z=Z$
. So suppose that
$[\{f^l\}_{l\in I'}, \{g^l\}_{l\in I'}]^I_Z=Z$
. So suppose that
![]() $|I'|>0$
and choose
$|I'|>0$
and choose
![]() $i\in I'$
and set
$i\in I'$
and set
![]() $J=I$
and
$J=I$
and
![]() $J'=I'\setminus \{i\}$
. Then
$J'=I'\setminus \{i\}$
. Then
![]() $X=[\{f^l\}_{l\in J'},\{g^l\}_{l\in J'}]^J_Z\subseteq M^{m-1}$
is definably normal by the induction hypothesis.
$X=[\{f^l\}_{l\in J'},\{g^l\}_{l\in J'}]^J_Z\subseteq M^{m-1}$
is definably normal by the induction hypothesis.
Now let
![]() $F\colon X\to M$
be given by
$F\colon X\to M$
be given by
![]() $F(u)=f^{i}\circ \pi _{J'}(u)$
and
$F(u)=f^{i}\circ \pi _{J'}(u)$
and
![]() $G\colon X\to M$
be given by
$G\colon X\to M$
be given by
![]() $G(u)=g^i \circ \pi _{J'}(u)$
. Then F and G are continuous definable functions,
$G(u)=g^i \circ \pi _{J'}(u)$
. Then F and G are continuous definable functions,
![]() $F\circ \pi _{i}(x)=f^i\circ \pi _{J'}(\pi _{i}(x))=f^i\circ \pi _{I'}(x)$
and
$F\circ \pi _{i}(x)=f^i\circ \pi _{J'}(\pi _{i}(x))=f^i\circ \pi _{I'}(x)$
and
![]() $G\circ \pi _{i}(x)=g^i\circ \pi _{I'}(x)$
. Therefore,
$G\circ \pi _{i}(x)=g^i\circ \pi _{I'}(x)$
. Therefore,
and so, by Proposition 4.21, this set is definably normal.
To proceed, we need to recall the following results:
Fact 4.23 [Reference Edmundo, Mamino, Prelli, Ramakrishnan and Terzo24, Theorem 2.2].
Let U be an open definable subset of
![]() $M^m$
. Then U is a finite union of open definable sets definably homeomorphic, after possibly reordering of coordinates, to open cells.
$M^m$
. Then U is a finite union of open definable sets definably homeomorphic, after possibly reordering of coordinates, to open cells.
![]() $\Box $
$\Box $
Let
![]() $\pi \colon M^m \to M^{m-1}$
be the projection onto the first
$\pi \colon M^m \to M^{m-1}$
be the projection onto the first
![]() $m-1$
coordinates. Clearly, the following also holds with
$m-1$
coordinates. Clearly, the following also holds with
![]() $\pi $
replaced by each
$\pi $
replaced by each
![]() $\pi _i\colon M^m\to M^{m-1}$
as defined above.
$\pi _i\colon M^m\to M^{m-1}$
as defined above.
Fact 4.24 [Reference Dinis, Edmundo and Mamino19, Theorem 3.4].
Let U be an open definable subset of
![]() $M^m$
. Then there is a finite cover
$M^m$
. Then there is a finite cover
![]() $\{U_j:j=1,\ldots , l\}$
of
$\{U_j:j=1,\ldots , l\}$
of
![]() $\pi (U)$
by open definable subsets such that for each i there is a continuous definable section
$\pi (U)$
by open definable subsets such that for each i there is a continuous definable section
![]() $s_j\colon U_j\to U$
of
$s_j\colon U_j\to U$
of
![]() $\pi $
(i.e.,
$\pi $
(i.e.,
![]() $\pi \circ s_j=\mathrm {id}_{U_j}$
).
$\pi \circ s_j=\mathrm {id}_{U_j}$
).
![]() $\Box $
$\Box $
We now go back to the setting
![]() ${\mathbf {\Gamma }}$
,
${\mathbf {\Gamma }}$
,
![]() ${\mathbf {\Gamma }_{\infty } }$
and
${\mathbf {\Gamma }_{\infty } }$
and
![]() ${\mathbf {\Sigma }}$
. Note that by the several remarks made previously regarding definability and definable topological notions (including connectedness, compactness, normality), we may safely omit the prefix
${\mathbf {\Sigma }}$
. Note that by the several remarks made previously regarding definability and definable topological notions (including connectedness, compactness, normality), we may safely omit the prefix
![]() ${\mathbf {\Gamma }}$
(respectively,
${\mathbf {\Gamma }}$
(respectively,
![]() ${\mathbf {\Gamma }_{\infty } }$
and
${\mathbf {\Gamma }_{\infty } }$
and
![]() ${\mathbf {\Sigma }}$
) and simply say definable (respectively, definably connected, definably compact, definably normal) when talking about subsets of
${\mathbf {\Sigma }}$
) and simply say definable (respectively, definably connected, definably compact, definably normal) when talking about subsets of
![]() ${\Gamma ^m}$
or
${\Gamma ^m}$
or
![]() ${\Gamma ^m_{\infty } }$
and
${\Gamma ^m_{\infty } }$
and
![]() ${\Sigma ^m}$
.
${\Sigma ^m}$
.
Recall that given
![]() $I\subseteq \{1,\ldots , m\}$
,
$I\subseteq \{1,\ldots , m\}$
,
![]() $I'=\{1,\ldots ,m\}\setminus I,$
$I'=\{1,\ldots ,m\}\setminus I,$
is the projection omitting the coordinates in I and
is the projection onto the coordinates in I (so
![]() $\pi ^{\prime }_I=\pi _{I'}$
). If
$\pi ^{\prime }_I=\pi _{I'}$
). If
![]() $Z\subseteq \Sigma ^{|I|}$
is a definable set and
$Z\subseteq \Sigma ^{|I|}$
is a definable set and
![]() $\{f^l\colon Z\to {\Sigma }\}_{l\in I'}$
a family of continuous definable functions, we set
$\{f^l\colon Z\to {\Sigma }\}_{l\in I'}$
a family of continuous definable functions, we set
Also recall that, if
![]() $I=\{1,\ldots , m\},$
then
$I=\{1,\ldots , m\},$
then
![]() $(\{f^l\}_{l\in I'},\infty ]^I_Z=Z$
.
$(\{f^l\}_{l\in I'},\infty ]^I_Z=Z$
.
Proposition 4.25. Let
![]() $O\subseteq {\Gamma ^m_{\infty } }$
be an open definable subset. Then O is a finite union of open definable subsets of the form
$O\subseteq {\Gamma ^m_{\infty } }$
be an open definable subset. Then O is a finite union of open definable subsets of the form
![]() $(\{f^l_V\}_{l\in I'},\infty ]^I_{V}$
with
$(\{f^l_V\}_{l\in I'},\infty ]^I_{V}$
with
![]() $I\subseteq \{1,\ldots , m\}$
and V an open definable subset of
$I\subseteq \{1,\ldots , m\}$
and V an open definable subset of
![]() $\Gamma ^{|I|}$
.
$\Gamma ^{|I|}$
.
Proof. Let
![]() $I\subsetneq \{1,\ldots , m\}$
be such that
$I\subsetneq \{1,\ldots , m\}$
be such that
![]() $O_I\neq \emptyset $
. For
$O_I\neq \emptyset $
. For
![]() $A\subseteq \tau _I(O_I)$
and
$A\subseteq \tau _I(O_I)$
and
![]() $B\subseteq \Gamma _{\infty }^{|I'|}$
, we let
$B\subseteq \Gamma _{\infty }^{|I'|}$
, we let
![]() $A\star _I B$
denote the set defined by
$A\star _I B$
denote the set defined by
 $$\begin{align*}(a_1,\ldots, a_m)\in A\star _I B \Leftrightarrow \begin{cases} a_i\in B & \text{ if } i\in I' \\ a_i\in \pi_i'(A) & \text{ if } i\in I, \end{cases} \end{align*}$$
$$\begin{align*}(a_1,\ldots, a_m)\in A\star _I B \Leftrightarrow \begin{cases} a_i\in B & \text{ if } i\in I' \\ a_i\in \pi_i'(A) & \text{ if } i\in I, \end{cases} \end{align*}$$
where
![]() $\pi _i'\colon \tau _I(O_I)\to \Gamma $
is the restriction of the projection onto the ith coordinate. Consider the definable set
$\pi _i'\colon \tau _I(O_I)\to \Gamma $
is the restriction of the projection onto the ith coordinate. Consider the definable set
 $$\begin{align*}U_I:= \left\{(a,b)\in \tau_I(O_I)\times \Gamma: \begin{array}{l} \text{there is an open neighbourhood } U \text{ of } a \text{ in } \tau_I(O_I) \\ \text{and } c\in \Gamma \text{ such that } c<b \text{ and } U\star _I (c,\infty]^{|I'|}\subseteq O \end{array} \right\}. \end{align*}$$
$$\begin{align*}U_I:= \left\{(a,b)\in \tau_I(O_I)\times \Gamma: \begin{array}{l} \text{there is an open neighbourhood } U \text{ of } a \text{ in } \tau_I(O_I) \\ \text{and } c\in \Gamma \text{ such that } c<b \text{ and } U\star _I (c,\infty]^{|I'|}\subseteq O \end{array} \right\}. \end{align*}$$
Let
![]() $\pi \colon U_I\to \tau _I(O_I)\subseteq \Gamma ^{|I|}$
be the projection to the first
$\pi \colon U_I\to \tau _I(O_I)\subseteq \Gamma ^{|I|}$
be the projection to the first
![]() $|I|$
-coordinates.
$|I|$
-coordinates.
Claim 4.26.
![]() $\pi (U_I)=\tau _I(O_I)$
.
$\pi (U_I)=\tau _I(O_I)$
.
The left-to-right inclusion is trivial. From right to left, let a be an element of
![]() $\tau _I(O_I)$
. Then there is
$\tau _I(O_I)$
. Then there is
![]() $a'\in O$
such that
$a'\in O$
such that
![]() $\tau _I(a')=a$
. Since O is open, let
$\tau _I(a')=a$
. Since O is open, let
![]() $V=\prod _{i=1}^m J_i\subseteq O$
be a product of basic open sets containing
$V=\prod _{i=1}^m J_i\subseteq O$
be a product of basic open sets containing
![]() $a'$
. Then
$a'$
. Then
![]() $U:= \tau _I(V)$
is a neighbourhood of a in
$U:= \tau _I(V)$
is a neighbourhood of a in
![]() $\tau _I(O_I)$
. Moreover, for
$\tau _I(O_I)$
. Moreover, for
![]() $i\in I'$
, we may suppose
$i\in I'$
, we may suppose
![]() $J_i=(b_i,\infty ]$
for some
$J_i=(b_i,\infty ]$
for some
![]() $b_i\in \Gamma $
. Let
$b_i\in \Gamma $
. Let
![]() $c=\max \{b_i: i\in I'\}$
. Then
$c=\max \{b_i: i\in I'\}$
. Then
![]() $U\star _I (c,\infty ]^{|I'|}\subseteq O$
. In particular,
$U\star _I (c,\infty ]^{|I'|}\subseteq O$
. In particular,
![]() $(a,b)\in U_I$
for every element
$(a,b)\in U_I$
for every element
![]() $b\in (c,\infty )$
, which shows that
$b\in (c,\infty )$
, which shows that
![]() $a\in \pi (U_I)$
. This proves the claim.
$a\in \pi (U_I)$
. This proves the claim.
Claim 4.27. The set
![]() $U_I$
is open.
$U_I$
is open.
Let
![]() $(a,b)$
be an element in
$(a,b)$
be an element in
![]() $U_I$
. By definition, let U be a neighbourhood of a in
$U_I$
. By definition, let U be a neighbourhood of a in
![]() $\tau _I(O_I)$
and
$\tau _I(O_I)$
and
![]() $c\in \Gamma $
such that
$c\in \Gamma $
such that
![]() $c<b$
and
$c<b$
and
![]() $U\star _I (c,\infty ]^{|I'|}\subseteq O$
. We let the reader verify that
$U\star _I (c,\infty ]^{|I'|}\subseteq O$
. We let the reader verify that
![]() $U\times (c,\infty )\subseteq U_I$
, which shows the claim.
$U\times (c,\infty )\subseteq U_I$
, which shows the claim.
By Fact 4.24 applied to
![]() $U_I$
and the projection
$U_I$
and the projection
![]() $\pi \colon U_I\to \Gamma ^{|I|}$
, there exists a finite cover
$\pi \colon U_I\to \Gamma ^{|I|}$
, there exists a finite cover
![]() ${\mathcal {V}}_I$
of
${\mathcal {V}}_I$
of
![]() $\pi (U_I)=\tau _I(O_I)$
by open definable subsets, and for each
$\pi (U_I)=\tau _I(O_I)$
by open definable subsets, and for each
![]() $V\in {\mathcal {V}}_I$
, there is a continuous definable section
$V\in {\mathcal {V}}_I$
, there is a continuous definable section
![]() $s_V\colon V\to U_I$
of
$s_V\colon V\to U_I$
of
![]() $\pi $
. We let the reader verify that the previous claims imply that the family
$\pi $
. We let the reader verify that the previous claims imply that the family
is a finite family of open definable subsets of O covering
![]() $O_I$
.
$O_I$
.
The union of
![]() $O_{\{1\,\ldots ,m\}}$
and all families as in equation (*) for all
$O_{\{1\,\ldots ,m\}}$
and all families as in equation (*) for all
![]() $I\subsetneq \{1,\ldots ,m\}$
provide the required family of open sets.
$I\subsetneq \{1,\ldots ,m\}$
provide the required family of open sets.
We are finally ready to prove the main goal of this subsection:
Theorem 4.28. Suppose that
![]() ${\mathbf {\Gamma }}=({\Gamma }, <, +, \ldots )$
is an o-minimal expansion of an ordered group
${\mathbf {\Gamma }}=({\Gamma }, <, +, \ldots )$
is an o-minimal expansion of an ordered group
![]() $({\Gamma } , <, + )$
. Let Z be a definably locally closed subset of
$({\Gamma } , <, + )$
. Let Z be a definably locally closed subset of
![]() ${\Gamma ^m_{\infty } }$
. Then Z is the union of finitely many relatively open definable subsets that are definably normal.
${\Gamma ^m_{\infty } }$
. Then Z is the union of finitely many relatively open definable subsets that are definably normal.
Proof. Since a definably locally closed set is of the form
![]() $O\cap S$
with O open definable and S closed definable, it is a closed definable subset of an open definable subset. Therefore it is enough to prove the result for an open definable subset O of
$O\cap S$
with O open definable and S closed definable, it is a closed definable subset of an open definable subset. Therefore it is enough to prove the result for an open definable subset O of
![]() ${\Gamma ^m_{\infty } }$
.
${\Gamma ^m_{\infty } }$
.
By Proposition 4.25, it is enough to show that open definable subsets of O of the form
![]() $(\{f^l_V\}_{l\in I'},\infty ]^I_{V}$
with
$(\{f^l_V\}_{l\in I'},\infty ]^I_{V}$
with
![]() $I\subseteq \{1,\ldots , m\}$
and V an open definable subset of
$I\subseteq \{1,\ldots , m\}$
and V an open definable subset of
![]() $\Gamma ^{|I|}$
are definably normal. So fix
$\Gamma ^{|I|}$
are definably normal. So fix
![]() $I\subseteq \{1,\ldots , m\}$
and V an open definable subset of
$I\subseteq \{1,\ldots , m\}$
and V an open definable subset of
![]() $\Gamma ^{|I|}$
. If
$\Gamma ^{|I|}$
. If
![]() $I'=\emptyset ,$
the
$I'=\emptyset ,$
the
![]() $(\{f^l_V\}_{l\in I'},\infty ]^I_{V}=V\subseteq {\Gamma ^m}$
is definably normal (Remark 4.14). Suppose otherwise, let
$(\{f^l_V\}_{l\in I'},\infty ]^I_{V}=V\subseteq {\Gamma ^m}$
is definably normal (Remark 4.14). Suppose otherwise, let
![]() $P=(\{f^l_V\}_{l\in I'},\infty ]^I_{V}$
, and consider
$P=(\{f^l_V\}_{l\in I'},\infty ]^I_{V}$
, and consider
and
Since
![]() $X, Y\subseteq {\Gamma ^m},$
by Remark 4.14, they are both definably normal, and by Theorem 4.22, Z is also definably normal.
$X, Y\subseteq {\Gamma ^m},$
by Remark 4.14, they are both definably normal, and by Theorem 4.22, Z is also definably normal.
Let
![]() $C,D\subseteq P$
be closed, disjoint definable subsets. Since
$C,D\subseteq P$
be closed, disjoint definable subsets. Since
![]() $C\cap Y, D\cap Y\subseteq Y$
are closed, disjoint definable subsets and Y is definably normal, there are
$C\cap Y, D\cap Y\subseteq Y$
are closed, disjoint definable subsets and Y is definably normal, there are
![]() $U_Y,V_Y\subseteq Y$
open, disjoint definable subsets of Y such that
$U_Y,V_Y\subseteq Y$
open, disjoint definable subsets of Y such that
![]() $C\cap Y\subseteq U_Y$
and
$C\cap Y\subseteq U_Y$
and
![]() $D\cap Y\subseteq V_Y$
. Similarly, there are
$D\cap Y\subseteq V_Y$
. Similarly, there are
![]() $U_Z, V_Z\subseteq Z$
open, disjoint definable subsets of Z such that
$U_Z, V_Z\subseteq Z$
open, disjoint definable subsets of Z such that
![]() $C\cap Z\subseteq U_Z$
and
$C\cap Z\subseteq U_Z$
and
![]() $D\cap Z\subseteq V_Z$
, and there are
$D\cap Z\subseteq V_Z$
, and there are
![]() $U_X, V_X\subseteq X$
open, disjoint definable subsets of X such that
$U_X, V_X\subseteq X$
open, disjoint definable subsets of X such that
![]() $C\cap X\subseteq U_X$
and
$C\cap X\subseteq U_X$
and
![]() $D\cap X\subseteq V_X$
. Again, by definable normality, let
$D\cap X\subseteq V_X$
. Again, by definable normality, let
![]() $U^{\prime }_X\subseteq X$
be an open definable subset of X such that
$U^{\prime }_X\subseteq X$
be an open definable subset of X such that
![]() $C\cap X\subseteq U^{\prime }_X\subseteq \overline {U^{\prime }_X}\subseteq U_X$
, and similarly let
$C\cap X\subseteq U^{\prime }_X\subseteq \overline {U^{\prime }_X}\subseteq U_X$
, and similarly let
![]() $U^{\prime }_Z\subseteq Z$
be an open definable subset of Z such that
$U^{\prime }_Z\subseteq Z$
be an open definable subset of Z such that
![]() $C\cap Z\subseteq U^{\prime }_Z\subseteq \overline {U^{\prime }_Z}\subseteq U_Z$
and let
$C\cap Z\subseteq U^{\prime }_Z\subseteq \overline {U^{\prime }_Z}\subseteq U_Z$
and let
![]() $U^{\prime }_Y\subseteq Y$
be an open definable subset of Y such that
$U^{\prime }_Y\subseteq Y$
be an open definable subset of Y such that
![]() $C\cap Y\subseteq U^{\prime }_Y\subseteq \overline {U^{\prime }_Y}\subseteq U_Y$
.
$C\cap Y\subseteq U^{\prime }_Y\subseteq \overline {U^{\prime }_Y}\subseteq U_Y$
.
Let
![]() $V^{\prime }_Y=V_Y\setminus (\overline {U^{\prime }_Z}\cup \overline {U^{\prime }_X}), \ V^{\prime }_X=V_X\setminus (\overline {U^{\prime }_Y}\cup \overline {U^{\prime }_Z})$
and
$V^{\prime }_Y=V_Y\setminus (\overline {U^{\prime }_Z}\cup \overline {U^{\prime }_X}), \ V^{\prime }_X=V_X\setminus (\overline {U^{\prime }_Y}\cup \overline {U^{\prime }_Z})$
and
![]() $V^{\prime }_Z=V_Z\setminus (\overline {U^{\prime }_Y}\cup \overline {U^{\prime }_X})$
. Let
$V^{\prime }_Z=V_Z\setminus (\overline {U^{\prime }_Y}\cup \overline {U^{\prime }_X})$
. Let
We have that Q is a closed definable subset of P and of Y (the
![]() $f^l_V$
s are continuous). Let
$f^l_V$
s are continuous). Let
![]() $U^{\prime \prime }_Z=U^{\prime }_Z\setminus Q$
, and let
$U^{\prime \prime }_Z=U^{\prime }_Z\setminus Q$
, and let
![]() $V^{\prime \prime }_Z=V^{\prime }_Z\setminus Q$
.
$V^{\prime \prime }_Z=V^{\prime }_Z\setminus Q$
.
Let
![]() $U=U^{\prime }_Y\cup U^{\prime \prime }_Z\cup U^{\prime }_X$
, and let
$U=U^{\prime }_Y\cup U^{\prime \prime }_Z\cup U^{\prime }_X$
, and let
![]() $V=V^{\prime }_Y\cup V^{\prime \prime }_Z\cup V^{\prime }_X$
. Since
$V=V^{\prime }_Y\cup V^{\prime \prime }_Z\cup V^{\prime }_X$
. Since
![]() $C\cap Q\subseteq U^{\prime }_Y$
, we clearly have
$C\cap Q\subseteq U^{\prime }_Y$
, we clearly have
![]() $C\subseteq U$
. On the other hand,
$C\subseteq U$
. On the other hand,
![]() $D\cap \overline {U^{\prime }_X}=D\cap \overline {U^{\prime }_Z}=D\cap \overline {U^{\prime }_Y}=\emptyset $
; otherwise,
$D\cap \overline {U^{\prime }_X}=D\cap \overline {U^{\prime }_Z}=D\cap \overline {U^{\prime }_Y}=\emptyset $
; otherwise,
![]() $D\cap U_X\neq \emptyset $
and
$D\cap U_X\neq \emptyset $
and
![]() $U_X\cap V_X\neq \emptyset $
or, similarly,
$U_X\cap V_X\neq \emptyset $
or, similarly,
![]() $U_Z\cap V_Z\neq \emptyset $
or
$U_Z\cap V_Z\neq \emptyset $
or
![]() $U_Y\cap V_Y\neq \emptyset $
. Thus, since
$U_Y\cap V_Y\neq \emptyset $
. Thus, since
![]() $D\cap Q\subseteq V^{\prime }_Y,$
we also have
$D\cap Q\subseteq V^{\prime }_Y,$
we also have
![]() $D\subseteq V$
. By construction, we have
$D\subseteq V$
. By construction, we have
![]() $U\cap V=\emptyset $
. Now
$U\cap V=\emptyset $
. Now
![]() $U^{\prime }_Y$
is open in Y and Y is open in
$U^{\prime }_Y$
is open in Y and Y is open in
![]() $P, \ U^{\prime }_X$
is open in X and X is open in P, and
$P, \ U^{\prime }_X$
is open in X and X is open in P, and
![]() $U^{\prime \prime }_Z$
is the interior of
$U^{\prime \prime }_Z$
is the interior of
![]() $U^{\prime }_Z$
in
$U^{\prime }_Z$
in
![]() $P,$
so U is open in P. Similarly, V is open in P.
$P,$
so U is open in P. Similarly, V is open in P.
5 Sites on definable sets and in their stable completions in ACVF
In this section, we will introduce the
![]() $\mathrm {v\!+\!g}$
-site on definable sets of algebraically closed nontrivially valued fields and the
$\mathrm {v\!+\!g}$
-site on definable sets of algebraically closed nontrivially valued fields and the
![]() $\widehat {\mathrm {v\!+\!g}}$
-site on their corresponding stable completion. We will further show that the latter forms a
$\widehat {\mathrm {v\!+\!g}}$
-site on their corresponding stable completion. We will further show that the latter forms a
![]() ${\mathcal {T}}$
-space in the sense of Section 3. Definable compactness and normality will be discussed in Subsection 5.4.
${\mathcal {T}}$
-space in the sense of Section 3. Definable compactness and normality will be discussed in Subsection 5.4.
We begin by recalling the needed model-theoretic background on ACVF. Some familiarity with valued fields and their model-theory will be assumed, however. For further references, we refer the reader to [Reference Prestel and Roquette51] or [Reference Haskell, Hrushovski and Macpherson33].
5.1 Preliminaries on ACVF
Let
![]() ${\mathcal {L}}_{k, {\Gamma }}$
be the three sorted languages of valued fields: in both the valued field sort
${\mathcal {L}}_{k, {\Gamma }}$
be the three sorted languages of valued fields: in both the valued field sort
![]() $\mathbf {VF}$
and the residue field sort k, we put the language of rings
$\mathbf {VF}$
and the residue field sort k, we put the language of rings
![]() ${\mathcal {L}}_{\mathrm {ring}}$
, and in the value group sort
${\mathcal {L}}_{\mathrm {ring}}$
, and in the value group sort
![]() $\Gamma _{\infty }$
, the language
$\Gamma _{\infty }$
, the language
![]() ${\mathcal {L}}_{\mathrm {og}}^{\infty }$
of ordered groups with an additional constant symbol for
${\mathcal {L}}_{\mathrm {og}}^{\infty }$
of ordered groups with an additional constant symbol for
![]() $\infty $
, together with symbols for the valuation
$\infty $
, together with symbols for the valuation
![]() $\mathrm {val}$
and the map
$\mathrm {val}$
and the map
![]() $\mathrm {Res}\colon \mathbf {VF}^2\to k$
sending
$\mathrm {Res}\colon \mathbf {VF}^2\to k$
sending
![]() $(x,y)$
to
$(x,y)$
to
![]() $\mathrm {res}(xy^{-1})$
if
$\mathrm {res}(xy^{-1})$
if
![]() $\mathrm {val}(x)\geq \mathrm {val}(y)$
and
$\mathrm {val}(x)\geq \mathrm {val}(y)$
and
![]() $y\neq 0$
and to
$y\neq 0$
and to
![]() $0$
otherwise.
$0$
otherwise.
Let
![]() ${\mathcal {L}}_{{\mathcal {G}}}$
be the geometric language extending
${\mathcal {L}}_{{\mathcal {G}}}$
be the geometric language extending
![]() ${\mathcal {L}}_{k, {\Gamma }}$
with new sorts described in [Reference Haskell, Hrushovski and Macpherson32, Section 3.1]. By [Reference Haskell, Hrushovski and Macpherson33, Theorem 2.1.1], the theory ACVF of algebraically closed fields with a nontrivial valuation has quantifier elimination in the language
${\mathcal {L}}_{k, {\Gamma }}$
with new sorts described in [Reference Haskell, Hrushovski and Macpherson32, Section 3.1]. By [Reference Haskell, Hrushovski and Macpherson33, Theorem 2.1.1], the theory ACVF of algebraically closed fields with a nontrivial valuation has quantifier elimination in the language
![]() ${\mathcal {L}} _{k, {\Gamma }}$
; and by [Reference Haskell, Hrushovski and Macpherson33, Theorem 7.3], it has quantifier elimination and elimination of imaginaries in the language
${\mathcal {L}} _{k, {\Gamma }}$
; and by [Reference Haskell, Hrushovski and Macpherson33, Theorem 7.3], it has quantifier elimination and elimination of imaginaries in the language
![]() ${\mathcal {L}}_{{\mathcal {G}}}$
.
${\mathcal {L}}_{{\mathcal {G}}}$
.
Below, we fix a monster model
![]() $\mathbb {U}$
of ACVF in the language
$\mathbb {U}$
of ACVF in the language
![]() ${\mathcal {L}} _{{\mathcal {G}}}$
and assume that all sets of parameters we consider are small substructures C of
${\mathcal {L}} _{{\mathcal {G}}}$
and assume that all sets of parameters we consider are small substructures C of
![]() $\mathbb {U}$
(i.e., subsets C of
$\mathbb {U}$
(i.e., subsets C of
![]() $\mathbb {U}$
such that
$\mathbb {U}$
such that
![]() $\mathrm {dcl}(C)=C$
and
$\mathrm {dcl}(C)=C$
and
![]() $|C|<|\mathbb {U}|$
) and all models K of ACVF considered are elementary substructures of
$|C|<|\mathbb {U}|$
) and all models K of ACVF considered are elementary substructures of
![]() $\mathbb {U}$
, again of smaller cardinality. By
$\mathbb {U}$
, again of smaller cardinality. By
![]() $\mathcal {R}$
,
$\mathcal {R}$
,
![]() $\mathcal {M}$
and k, we mean the valuation ring, its maximal ideal and the residue field in
$\mathcal {M}$
and k, we mean the valuation ring, its maximal ideal and the residue field in
![]() $\mathbb {U}$
.
$\mathbb {U}$
.
It is worth noting that over an elementary small substructure K of
![]() $\mathbb {U}$
, the residue field and the value group are stably embedded: that is, every definable subset of
$\mathbb {U}$
, the residue field and the value group are stably embedded: that is, every definable subset of
![]() ${\Gamma ^n_{\infty } }(K)$
(respectively,
${\Gamma ^n_{\infty } }(K)$
(respectively,
![]() $k(K)^n$
) is already definable in
$k(K)^n$
) is already definable in
![]() $(\Gamma _{\infty }(K)$
,
$(\Gamma _{\infty }(K)$
,
![]() ${\mathcal {L}}_{\mathrm {og}}^{\infty })$
(respectively,
${\mathcal {L}}_{\mathrm {og}}^{\infty })$
(respectively,
![]() $(k(K),{\mathcal {L}}_{\mathrm {ring}})$
). See [Reference Haskell, Hrushovski and Macpherson32, Proposition 2.1.3].
$(k(K),{\mathcal {L}}_{\mathrm {ring}})$
). See [Reference Haskell, Hrushovski and Macpherson32, Proposition 2.1.3].
Let C be a small substructure of
![]() $\mathbb {U}$
. By an algebraic variety V over C, we mean the set of
$\mathbb {U}$
. By an algebraic variety V over C, we mean the set of
![]() $\mathbb {U}$
-closed points of a separated reduced scheme of finite type over the valued field sort of C (e.g.,
$\mathbb {U}$
-closed points of a separated reduced scheme of finite type over the valued field sort of C (e.g.,
![]() $\mathbb {A}^n$
stands for
$\mathbb {A}^n$
stands for
![]() $\mathbb {U}^n$
). By an algebraic variety, we mean an algebraic variety V over some small substructure C. Note that the category of separated reduced schemes of finite type over
$\mathbb {U}^n$
). By an algebraic variety, we mean an algebraic variety V over some small substructure C. Note that the category of separated reduced schemes of finite type over
![]() $\mathbb {U}$
and the category of their
$\mathbb {U}$
and the category of their
![]() $\mathbb {U}$
-closed points are equivalent (see [Reference Hartshorne31, Proposition 2.6]).
$\mathbb {U}$
-closed points are equivalent (see [Reference Hartshorne31, Proposition 2.6]).
Given an algebraic variety V over C, there are finitely many charts
![]() $(V_i, U_i, f_i)_{i\leq m}$
such that (i)
$(V_i, U_i, f_i)_{i\leq m}$
such that (i)
![]() $V=V_1\cup \ldots \cup V_m$
; (ii) each
$V=V_1\cup \ldots \cup V_m$
; (ii) each
![]() $f_i:V_i\to U_i$
is a isomorphism with
$f_i:V_i\to U_i$
is a isomorphism with
![]() $U_i\subseteq \mathbb {A}^{n_i}$
an affine variety over C; (iii)
$U_i\subseteq \mathbb {A}^{n_i}$
an affine variety over C; (iii)
![]() $U_{ij}=f_i(V_i\cap V_j)$
is a Zariski open subset of
$U_{ij}=f_i(V_i\cap V_j)$
is a Zariski open subset of
![]() $U_i$
; and (iv)
$U_i$
; and (iv)
![]() $f_j\circ f_i^{-1}$
is an isomorphism between the quasi-affine varieties
$f_j\circ f_i^{-1}$
is an isomorphism between the quasi-affine varieties
![]() $U_{ij}$
and
$U_{ij}$
and
![]() $U_{ji}$
over C. If W is another variety over C, then
$U_{ji}$
over C. If W is another variety over C, then
![]() $f:V\to W$
is a morphism if and only if, for some charts
$f:V\to W$
is a morphism if and only if, for some charts
![]() $(W_j, U^{\prime }_j, g_j)_{j\leq k}$
for W, each
$(W_j, U^{\prime }_j, g_j)_{j\leq k}$
for W, each
![]() $(g_j\circ f\circ f_i^{-1})_{|}:f_i(f^{-1}(W_j)\cap U_i) \to g_j(U^{\prime }_j)$
is a morphism of quasi-affine varieties over C. As in [Reference Pillay47, Section 3], by a C-definable subset of V, we mean a subset S such that for each i,
$(g_j\circ f\circ f_i^{-1})_{|}:f_i(f^{-1}(W_j)\cap U_i) \to g_j(U^{\prime }_j)$
is a morphism of quasi-affine varieties over C. As in [Reference Pillay47, Section 3], by a C-definable subset of V, we mean a subset S such that for each i,
![]() $f_i(S\cap V_i)$
is a C-definable subset of
$f_i(S\cap V_i)$
is a C-definable subset of
![]() $U_i$
. Note that this notion is independent of the choice of the charts.
$U_i$
. Note that this notion is independent of the choice of the charts.
By a C-definable set, we mean a C-definable subset of some product of sorts and of varieties over C in
![]() $\mathbb {U}$
. By a definable set, we mean a C-definable set for some small substructure C. We denote by
$\mathbb {U}$
. By a definable set, we mean a C-definable set for some small substructure C. We denote by
the category whose objects are C-definable sets and whose morphisms are C-definable maps between C-definable sets (i.e., maps between C-definable sets whose graphs are C-definable sets). Given a substructure F containing C, we have an inclusion functor
![]() $\mathrm {Def} _C\to \mathrm {Def} _F$
since every C-definable set is also F-definable.
$\mathrm {Def} _C\to \mathrm {Def} _F$
since every C-definable set is also F-definable.
Given an algebraic variety V with charts
![]() $(V_i, U_i, f_i)_{i\leq m}$
, we have that the Zariski topology on V:
$(V_i, U_i, f_i)_{i\leq m}$
, we have that the Zariski topology on V:
![]() $U\subseteq V$
is open if and only if each
$U\subseteq V$
is open if and only if each
![]() $f_i(U\cap V_i)$
is a Zariski open subset of
$f_i(U\cap V_i)$
is a Zariski open subset of
![]() $U_i$
. Besides the Zariski topology, we can also equip V with the valuation topology:
$U_i$
. Besides the Zariski topology, we can also equip V with the valuation topology:
![]() $U\subseteq V$
is open if and only if each
$U\subseteq V$
is open if and only if each
![]() $f_i(U\cap V_i)$
is an open subset of
$f_i(U\cap V_i)$
is an open subset of
![]() $U_i\subseteq \mathbb {A} ^{n_i}$
in the valuation topology. Recall that the valuation topology on
$U_i\subseteq \mathbb {A} ^{n_i}$
in the valuation topology. Recall that the valuation topology on
![]() $\mathbb {A} ^1$
is generated by the open balls
$\mathbb {A} ^1$
is generated by the open balls
centred at
![]() $a\in \mathbb {A}^1$
and with radius
$a\in \mathbb {A}^1$
and with radius
![]() $\gamma \in {\Gamma _{\infty } }$
, and the valuation topology on
$\gamma \in {\Gamma _{\infty } }$
, and the valuation topology on
![]() $\mathbb {A} ^n$
is the product topology. Note that these topologies are independent of the choice of the charts.
$\mathbb {A} ^n$
is the product topology. Note that these topologies are independent of the choice of the charts.
The valuation topology, however, is not suitable for developing cohomology as it is totally disconnected (the open balls are also closed sets) and not necessarily locally compact. In Subsection 5.2, we will introduce an appropriate site on a definable set that will replace the valuation topology. However, with this site, definable sets do not form a
![]() ${\mathcal {T}}$
-space. To obtain results for the cohomology theory on such sites, we have to go through another category associated to
${\mathcal {T}}$
-space. To obtain results for the cohomology theory on such sites, we have to go through another category associated to
![]() $\mathrm {Def} _C,$
the category of the stable completions of objects of
$\mathrm {Def} _C,$
the category of the stable completions of objects of
![]() $\mathrm {Def}_C$
with morphisms the C-pro-definable morphisms between such objects. We then introduce another site, isomorphic to the previous one, in the stable completion of a definable set. In Subsection 5.3, we show, using Hrushovski and Loeser’s main theorem, that the open sets of the site make the stable completion of a definable set into a
$\mathrm {Def}_C$
with morphisms the C-pro-definable morphisms between such objects. We then introduce another site, isomorphic to the previous one, in the stable completion of a definable set. In Subsection 5.3, we show, using Hrushovski and Loeser’s main theorem, that the open sets of the site make the stable completion of a definable set into a
![]() ${\mathcal {T}}$
-space. Finally, in Subsection 5.4, we show that in the stable completion of a definable set, for the associated notion of
${\mathcal {T}}$
-space. Finally, in Subsection 5.4, we show that in the stable completion of a definable set, for the associated notion of
![]() ${\mathcal {T}}$
-normality,
${\mathcal {T}}$
-normality,
![]() ${\mathcal {T}}$
-locally closed subsets are finite unions of
${\mathcal {T}}$
-locally closed subsets are finite unions of
![]() ${\mathcal {T}}$
-open subsets that are
${\mathcal {T}}$
-open subsets that are
![]() ${\mathcal {T}}$
-normal.
${\mathcal {T}}$
-normal.
In what follows, for simplicity, we will adopt the following conventions:
Remark 5.1. Let K be a small elementary substructure of
![]() $\mathbb {U}$
and X a K-definable set (e.g., a variety V over K). We write X for the set
$\mathbb {U}$
and X a K-definable set (e.g., a variety V over K). We write X for the set
![]() $X(\mathbb {U})$
of
$X(\mathbb {U})$
of
![]() $\mathbb {U}$
-points of X, and we write
$\mathbb {U}$
-points of X, and we write
![]() $X(K)$
for the set of K-points of X. Note that even though in what follows all definitions (respectively, results) are stated for
$X(K)$
for the set of K-points of X. Note that even though in what follows all definitions (respectively, results) are stated for
![]() $\mathbb {U}$
-points, they make sense (respectively, they hold) for K-points unless otherwise stated. In fact, a K-definable set X can also be seen as a functor from the category of all elementary extensions of K to the category of sets. The category of such functors is actually equivalent to the category of definable sets of
$\mathbb {U}$
-points, they make sense (respectively, they hold) for K-points unless otherwise stated. In fact, a K-definable set X can also be seen as a functor from the category of all elementary extensions of K to the category of sets. The category of such functors is actually equivalent to the category of definable sets of
![]() $\mathbb {U}$
of the form
$\mathbb {U}$
of the form
![]() $X(\mathbb {U})$
. Both points of view will be used indistinguishably in what follows. This justifies why we write X instead of
$X(\mathbb {U})$
. Both points of view will be used indistinguishably in what follows. This justifies why we write X instead of
![]() $X(\mathbb {U})$
. In case a statement involves two small elementary substructures K and
$X(\mathbb {U})$
. In case a statement involves two small elementary substructures K and
![]() $K'$
of
$K'$
of
![]() $\mathbb {U}$
, we will use the notation
$\mathbb {U}$
, we will use the notation
![]() $X(K)$
and
$X(K)$
and
![]() $X(K')$
to disambiguate.
$X(K')$
to disambiguate.
We treat
![]() ${\Gamma _{\infty } }$
,
${\Gamma _{\infty } }$
,
![]() $\mathcal {R}$
,
$\mathcal {R}$
,
![]() $\mathcal {M}$
and k as
$\mathcal {M}$
and k as
![]() $\emptyset $
-definable sets. Thus, following our convention, the set
$\emptyset $
-definable sets. Thus, following our convention, the set
![]() ${\Gamma _{\infty } }(K)$
(respectively,
${\Gamma _{\infty } }(K)$
(respectively,
![]() $\mathcal {R}(K)$
,
$\mathcal {R}(K)$
,
![]() $\mathcal {M}(K)$
and
$\mathcal {M}(K)$
and
![]() $k(K)$
) corresponds to the value group of
$k(K)$
) corresponds to the value group of
![]() $(K,\mathrm {val})$
(respectively, valuation ring, maximal ideal and residue field of
$(K,\mathrm {val})$
(respectively, valuation ring, maximal ideal and residue field of
![]() $(K,\mathrm {val})$
).
$(K,\mathrm {val})$
).
Given an algebraic variety V, we will consider the sheaf
![]() ${\mathcal {O}} _V$
(for the Zariski topology) of regular functions on V. Since, given charts
${\mathcal {O}} _V$
(for the Zariski topology) of regular functions on V. Since, given charts
![]() $(V_i, U_i, f_i)_{i\leq m}$
for V, the open subsets
$(V_i, U_i, f_i)_{i\leq m}$
for V, the open subsets
![]() $U\subseteq V_i$
for some i are a basis for the Zariski topology,
$U\subseteq V_i$
for some i are a basis for the Zariski topology,
![]() ${\mathcal {O}}_V$
is completely determined by the sheaves of regular functions
${\mathcal {O}}_V$
is completely determined by the sheaves of regular functions
![]() ${\mathcal {O}}_{U_i}$
on the quasi-affine varieties
${\mathcal {O}}_{U_i}$
on the quasi-affine varieties
![]() $U_i$
.
$U_i$
.
5.2 The
 $\mathrm {v\!+\!g}$
-sites
$\mathrm {v\!+\!g}$
-sites
We start with the definition of the site replacing the valuation topology. As we will explain below, this site is based on the work of Hrushovski and Loeser [Reference Hrushovski and Loeser35]. We then recall Hrushovski and Loeser’s category of the stable completions of objects of
![]() $\mathrm {Def}_C$
and the topology on such spaces. In general, this topology is also not suitable for cohomology (it is not locally compact), and we will replace it by a site as well.
$\mathrm {Def}_C$
and the topology on such spaces. In general, this topology is also not suitable for cohomology (it is not locally compact), and we will replace it by a site as well.
Definition 5.2 (The
 $\mathrm {v\!+\!g}$
-site).
$\mathrm {v\!+\!g}$
-site).
Let V be an algebraic variety. A subset of V is a basic
![]() $\mathrm {v\!+\!g}$
-open subset if it is of the form
$\mathrm {v\!+\!g}$
-open subset if it is of the form
 $$\begin{align*}\bigcap _{j\in J}\{u\in U_j:\mathrm{val} (f_j(u))<\mathrm{val} (g_j(u))\}, \end{align*}$$
$$\begin{align*}\bigcap _{j\in J}\{u\in U_j:\mathrm{val} (f_j(u))<\mathrm{val} (g_j(u))\}, \end{align*}$$
where J is a finite set and
![]() $f_j,g_j\in {\mathcal {O}} _V(U_j)$
are regular functions on a Zariski open subset
$f_j,g_j\in {\mathcal {O}} _V(U_j)$
are regular functions on a Zariski open subset
![]() $U_j\subseteq V$
. A subset of V is a
$U_j\subseteq V$
. A subset of V is a
![]() $\mathrm {v\!+\!g}$
-open subset if it is a finite union of basic
$\mathrm {v\!+\!g}$
-open subset if it is a finite union of basic
![]() $\mathrm {v\!+\!g}$
-open subsets; it is
$\mathrm {v\!+\!g}$
-open subsets; it is
![]() $\mathrm {v\!+\!g}$
-closed if it is the complement of a
$\mathrm {v\!+\!g}$
-closed if it is the complement of a
![]() $\mathrm {v\!+\!g}$
-open subset.
$\mathrm {v\!+\!g}$
-open subset.
A subset of
![]() $V\times {\Gamma ^m_{\infty } }$
is a basic
$V\times {\Gamma ^m_{\infty } }$
is a basic
![]() $\mathrm {v\!+\!g}$
-open subset if and only if its pullback under
$\mathrm {v\!+\!g}$
-open subset if and only if its pullback under
![]() $\mathrm {id} \times \mathrm {val}\colon V\times {\mathbb A} ^m\to V\times {\Gamma ^m_{\infty } }$
is a basic
$\mathrm {id} \times \mathrm {val}\colon V\times {\mathbb A} ^m\to V\times {\Gamma ^m_{\infty } }$
is a basic
![]() $\mathrm {v\!+\!g}$
-open subset of
$\mathrm {v\!+\!g}$
-open subset of
![]() $V\times {\mathbb A}^m; \ \mathrm {v\!+\!g}$
-open and
$V\times {\mathbb A}^m; \ \mathrm {v\!+\!g}$
-open and
![]() $\mathrm {v\!+\!g}$
-closed subsets of
$\mathrm {v\!+\!g}$
-closed subsets of
![]() $V\times {\Gamma ^m_{\infty } }$
are defined analogously.
$V\times {\Gamma ^m_{\infty } }$
are defined analogously.
If
![]() $X\subseteq V\times {\Gamma ^m_{\infty } }$
is a definable subset, we say that a subset of X is
$X\subseteq V\times {\Gamma ^m_{\infty } }$
is a definable subset, we say that a subset of X is
![]() $\mathrm {v\!+\!g}$
-open (respectively,
$\mathrm {v\!+\!g}$
-open (respectively,
![]() $\mathrm {v\!+\!g}$
-closed) if and only if it is of the form
$\mathrm {v\!+\!g}$
-closed) if and only if it is of the form
![]() $X\cap O$
(respectively,
$X\cap O$
(respectively,
![]() $X\cap D$
), where O (respectively, D) is a
$X\cap D$
), where O (respectively, D) is a
![]() $\mathrm {v\!+\!g}$
-open (respectively,
$\mathrm {v\!+\!g}$
-open (respectively,
![]() $\mathrm {v\!+\!g}$
-closed) subset of
$\mathrm {v\!+\!g}$
-closed) subset of
![]() $V\times {\Gamma ^m_{\infty } }$
. Similarly, a basic
$V\times {\Gamma ^m_{\infty } }$
. Similarly, a basic
![]() $\mathrm {v\!+\!g}$
-open subset of X is a set of the form
$\mathrm {v\!+\!g}$
-open subset of X is a set of the form
![]() $X\cap O$
, where O is basic
$X\cap O$
, where O is basic
![]() $\mathrm {v\!+\!g}$
-subset of
$\mathrm {v\!+\!g}$
-subset of
![]() $V\times {\Gamma ^m_{\infty } }$
.
$V\times {\Gamma ^m_{\infty } }$
.
The
![]() $\mathrm {v\!+\!g}$
-site on X, denoted
$\mathrm {v\!+\!g}$
-site on X, denoted
![]() $X_{\mathrm {v\!+\!g}},$
is the category
$X_{\mathrm {v\!+\!g}},$
is the category
![]() $\mathrm {Op}(X_{\mathrm {v\!+\!g}})$
whose objects are the
$\mathrm {Op}(X_{\mathrm {v\!+\!g}})$
whose objects are the
![]() $\mathrm {v\!+\!g}$
-open subsets of
$\mathrm {v\!+\!g}$
-open subsets of
![]() $X,$
the morphisms are the inclusions, and the admissible covers
$X,$
the morphisms are the inclusions, and the admissible covers
![]() $\mathrm {Cov}(U)$
of
$\mathrm {Cov}(U)$
of
![]() $U\in \mathrm {Op} (X_{\mathrm {v\!+\!g}})$
are covers by
$U\in \mathrm {Op} (X_{\mathrm {v\!+\!g}})$
are covers by
![]() $\mathrm {v\!+\!g}$
-open subsets of X with finite subcovers.
$\mathrm {v\!+\!g}$
-open subsets of X with finite subcovers.
Remark 5.3 (v-open and g-open subsets).
Note that if V is an algebraic variety, then:
-
- Since regular functions are continuous for the valuation topology, a
 $\mathrm {v\!+\!g}$
-open subset is v-open: that is, it is a definable subset that is open in the valuation topology.
$\mathrm {v\!+\!g}$
-open subset is v-open: that is, it is a definable subset that is open in the valuation topology. -
- Since the constant function zero is a regular function and
 $\mathrm {val} (f(u))<\infty $
is the same as
$\mathrm {val} (f(u))<\infty $
is the same as
 $f(u)\neq 0,$
it follows that a
$f(u)\neq 0,$
it follows that a
 $\mathrm {v\!+\!g}$
-open subset is g-open: that is, it is a positive finite Boolean combination of Zariski closed sets, Zariski open sets and sets of the form
$\mathrm {v\!+\!g}$
-open subset is g-open: that is, it is a positive finite Boolean combination of Zariski closed sets, Zariski open sets and sets of the form
 $\{u\in U:\mathrm {val} (f(u))<\mathrm {val} (g(u))\}$
with
$\{u\in U:\mathrm {val} (f(u))<\mathrm {val} (g(u))\}$
with
 $f, g\in {\mathcal {O}}_V(U)$
.
$f, g\in {\mathcal {O}}_V(U)$
.
Thus it follows from the characterisation of subsets that are both v-closed and g-closed when V is affine or projective ([Reference Hrushovski and Loeser35, Proposition 3.7.3]; see also below) that the
![]() $\mathrm {v\!+\!g}$
-open subsets as described above are exactly the subsets that are both v-open and g-open. The sets that are both v-open and g-open (respectively, v-closed and g-closed) are called in [Reference Hrushovski and Loeser35]
$\mathrm {v\!+\!g}$
-open subsets as described above are exactly the subsets that are both v-open and g-open. The sets that are both v-open and g-open (respectively, v-closed and g-closed) are called in [Reference Hrushovski and Loeser35]
![]() $\mathrm {v\!+\!g}$
-open subsets (respectively, v+g-closed subsets).
$\mathrm {v\!+\!g}$
-open subsets (respectively, v+g-closed subsets).
The following will be useful later:
Fact 5.4 [Reference Hrushovski and Loeser35, Proposition 3.7.3].
Let V be an affine (respectively, projective) algebraic variety. Then a subset of V is
![]() $\mathrm {v\!+\!g}$
-closed if and only if it is of the form
$\mathrm {v\!+\!g}$
-closed if and only if it is of the form
 $$\begin{align*}\bigcup _{i\in I}\bigcap _{j\in J}\{x\in V:h_{ij}(x)=0,\,\,\mathrm{val}(f_{ij}(x))\leq \mathrm{val}(g_{ij}(x))\},\end{align*}$$
$$\begin{align*}\bigcup _{i\in I}\bigcap _{j\in J}\{x\in V:h_{ij}(x)=0,\,\,\mathrm{val}(f_{ij}(x))\leq \mathrm{val}(g_{ij}(x))\},\end{align*}$$
where
![]() $I,J$
are finite and
$I,J$
are finite and
![]() $h_{ij}, f_{ij}, g_{ij}\in {\mathcal {O}}_V(V)$
are regular functions on V (respectively, homogeneous polynomials on V).
$h_{ij}, f_{ij}, g_{ij}\in {\mathcal {O}}_V(V)$
are regular functions on V (respectively, homogeneous polynomials on V).
![]() $\Box $
$\Box $
Remark 5.5 (
 $\mathrm {v\!+\!g}$
-opens and valuation topology).
$\mathrm {v\!+\!g}$
-opens and valuation topology).
The
![]() $\mathrm {v\!+\!g}$
-open subsets of an algebraic variety are a basis for the valuation topology. However, not every definable open subset is a
$\mathrm {v\!+\!g}$
-open subsets of an algebraic variety are a basis for the valuation topology. However, not every definable open subset is a
![]() $\mathrm {v\!+\!g}$
-open. For example, in
$\mathrm {v\!+\!g}$
-open. For example, in
![]() $\mathbb {A} ^1,$
the valuation ring
$\mathbb {A} ^1,$
the valuation ring
![]() ${\mathcal {R}}=\bigcup _{a\in {\mathcal {R}}}(a+{\mathcal {M}})$
is definable, open in the valuation topology but it is not
${\mathcal {R}}=\bigcup _{a\in {\mathcal {R}}}(a+{\mathcal {M}})$
is definable, open in the valuation topology but it is not
![]() $\mathrm {v\!+\!g}$
-open.
$\mathrm {v\!+\!g}$
-open.
In
![]() ${\Gamma ^m_{\infty } },$
by Fact 5.4, the
${\Gamma ^m_{\infty } },$
by Fact 5.4, the
![]() $\mathrm {v\!+\!g}$
-open subsets coincide with the open definable subsets of
$\mathrm {v\!+\!g}$
-open subsets coincide with the open definable subsets of
![]() ${\Gamma ^m_{\infty } }$
for the product of the order topology on
${\Gamma ^m_{\infty } }$
for the product of the order topology on
![]() ${\Gamma _{\infty } }$
(Remark 4.4). So the
${\Gamma _{\infty } }$
(Remark 4.4). So the
![]() $\mathrm {v\!+\!g}$
-site
$\mathrm {v\!+\!g}$
-site
![]() $X_{\mathrm {v\!+\!g}}$
on a definable subset
$X_{\mathrm {v\!+\!g}}$
on a definable subset
![]() $X\subseteq {\Gamma ^m_{\infty } }$
is the o-minimal site
$X\subseteq {\Gamma ^m_{\infty } }$
is the o-minimal site
![]() $X_{\mathrm {def}}$
as defined in Definition 4.8.
$X_{\mathrm {def}}$
as defined in Definition 4.8.
Remark 5.6 (Definable sets with the
 $\mathrm {v\!+\!g}$
-site are not
$\mathrm {v\!+\!g}$
-site are not
 ${\mathcal {T}}$
-spaces).
${\mathcal {T}}$
-spaces).
Let us say that a subset of a definable set of
![]() $V\times {\Gamma ^n_{\infty } }$
is a
$V\times {\Gamma ^n_{\infty } }$
is a
![]() $\mathrm {v\!+\!g}$
-subset if it is a finite boolean combination of
$\mathrm {v\!+\!g}$
-subset if it is a finite boolean combination of
![]() $\mathrm {v\!+\!g}$
-open subsets. Note that by quantifier elimination, the
$\mathrm {v\!+\!g}$
-open subsets. Note that by quantifier elimination, the
![]() $\mathrm {v\!+\!g}$
-subsets are exactly the definable subsets.
$\mathrm {v\!+\!g}$
-subsets are exactly the definable subsets.
It follows that the
![]() $\mathrm {v\!+\!g}$
-open subsets of a definable set of
$\mathrm {v\!+\!g}$
-open subsets of a definable set of
![]() $V\times {\Gamma ^n_{\infty } }$
do not form a
$V\times {\Gamma ^n_{\infty } }$
do not form a
![]() ${\mathcal {T}}$
-topology unless V is finite, since condition (iii) of Definition 3.2 fails: any
${\mathcal {T}}$
-topology unless V is finite, since condition (iii) of Definition 3.2 fails: any
![]() $\mathrm {v\!+\!g}$
-open is always a disjoint union of clopen
$\mathrm {v\!+\!g}$
-open is always a disjoint union of clopen
![]() $\mathrm {v\!+\!g}$
-subsets (i.e., definable subsets).
$\mathrm {v\!+\!g}$
-subsets (i.e., definable subsets).
For the reader’s convenience, below we recall the definition of the stable completion
![]() $\widehat {X}$
of a definable set X. When X is moreover a subset of
$\widehat {X}$
of a definable set X. When X is moreover a subset of
![]() $V\times {\Gamma ^n_{\infty } }$
for an algebraic variety V, we will equip
$V\times {\Gamma ^n_{\infty } }$
for an algebraic variety V, we will equip
![]() $\widehat {X}$
with a topology and a site, making
$\widehat {X}$
with a topology and a site, making
![]() $\widehat {X}$
into a
$\widehat {X}$
into a
![]() ${\mathcal {T}}$
-space.
${\mathcal {T}}$
-space.
Let B be any subset of
![]() $\mathbb {U}$
and x be a tuple of variables with length
$\mathbb {U}$
and x be a tuple of variables with length
![]() $|x|$
. We denote as usual by
$|x|$
. We denote as usual by
![]() $S_x(B)$
the space of types over B in the variables x: that is, the Stone space of the Boolean algebra of formulas with free variables contained in x and parameters from B up to equivalence over ACVF. If B is a model of ACVF, then
$S_x(B)$
the space of types over B in the variables x: that is, the Stone space of the Boolean algebra of formulas with free variables contained in x and parameters from B up to equivalence over ACVF. If B is a model of ACVF, then
![]() $S_x(B)$
can be characterised as the set of ultrafilters of definable subsets of
$S_x(B)$
can be characterised as the set of ultrafilters of definable subsets of
![]() $B^{|x|}$
over B.
$B^{|x|}$
over B.
Types in
![]() $S_x(\mathbb {U})$
are called global types. If C is a small substructure, a global type
$S_x(\mathbb {U})$
are called global types. If C is a small substructure, a global type
![]() $p\in S_x(\mathbb {U})$
is C-definable (or definable over C) if and only if for every
$p\in S_x(\mathbb {U})$
is C-definable (or definable over C) if and only if for every
![]() ${\mathcal {L}}_{{\mathcal {G}}}$
-formula
${\mathcal {L}}_{{\mathcal {G}}}$
-formula
![]() $\phi (x,y)$
there is an
$\phi (x,y)$
there is an
![]() ${\mathcal {L}}_{{\mathcal {G}}}$
-formula
${\mathcal {L}}_{{\mathcal {G}}}$
-formula
![]() $d_p(\phi )(y)$
over C such that for all
$d_p(\phi )(y)$
over C such that for all
![]() $b\in \mathbb {U} ^{|y|}$
, we have
$b\in \mathbb {U} ^{|y|}$
, we have
![]() $\phi (x,b)\in p$
if and only if
$\phi (x,b)\in p$
if and only if
![]() $d_p(\phi )(b)$
holds in
$d_p(\phi )(b)$
holds in
![]() $\mathbb {U}$
. Equivalently, since
$\mathbb {U}$
. Equivalently, since
![]() $\mathbb {U}$
is a model, a global type
$\mathbb {U}$
is a model, a global type
![]() $p\in S_x(\mathbb {U})$
is C-definable if and only if for every
$p\in S_x(\mathbb {U})$
is C-definable if and only if for every
![]() $\emptyset $
-definable family
$\emptyset $
-definable family
![]() $\{X_t\}_{t\in T}$
of definable subsets of
$\{X_t\}_{t\in T}$
of definable subsets of
![]() $\mathbb {U} ^{|x|}$
there is a C-definable subset
$\mathbb {U} ^{|x|}$
there is a C-definable subset
![]() $S\subseteq T$
such that
$S\subseteq T$
such that
![]() $X_t\in p$
if and only if
$X_t\in p$
if and only if
![]() $t\in S$
.
$t\in S$
.
A type
![]() $p\in S_x(B)$
concentrates on a C-definable set X if it contains a formula defining X. The notation
$p\in S_x(B)$
concentrates on a C-definable set X if it contains a formula defining X. The notation
![]() $S_X(B)$
is used to denote the subset of
$S_X(B)$
is used to denote the subset of
![]() $S_x(B)$
of all such types. Note if B is a model, then
$S_x(B)$
of all such types. Note if B is a model, then
![]() $S_X(B)$
can be identified with
$S_X(B)$
can be identified with
![]() $\widetilde {X(B)},$
the set of ultrafilters of definable subsets of
$\widetilde {X(B)},$
the set of ultrafilters of definable subsets of
![]() $X(B)$
over B; this notation was used in previous sections in the o-minimal setting.
$X(B)$
over B; this notation was used in previous sections in the o-minimal setting.
The stable completion of X over C, denoted by
![]() $\widehat {X}(C),$
can be characterised in ACVF as the set of C-definable global types concentrated on X that are orthogonal to
$\widehat {X}(C),$
can be characterised in ACVF as the set of C-definable global types concentrated on X that are orthogonal to
![]() $\Gamma $
. Recall that a global type p is orthogonal to
$\Gamma $
. Recall that a global type p is orthogonal to
![]() $\Gamma $
if and only if for every definable function
$\Gamma $
if and only if for every definable function
![]() $h\colon X\to {\Gamma _{\infty } } $
, the pushforward
$h\colon X\to {\Gamma _{\infty } } $
, the pushforward
![]() $h_*(p)$
is a global type concentrated on a point of
$h_*(p)$
is a global type concentrated on a point of
![]() $\Gamma _{\infty };$
the pushforward
$\Gamma _{\infty };$
the pushforward
![]() $h_*(p)$
is the global type given by
$h_*(p)$
is the global type given by
![]() $\{Z\subseteq \Gamma : Z\,\,\,\textrm {definable and}\,\,\,h^{-1}(Z)\in p\}$
. Also recall that, by ([Reference Hrushovski and Loeser35, Proposition 2.9.1], a C-definable global type p is orthogonal to
$\{Z\subseteq \Gamma : Z\,\,\,\textrm {definable and}\,\,\,h^{-1}(Z)\in p\}$
. Also recall that, by ([Reference Hrushovski and Loeser35, Proposition 2.9.1], a C-definable global type p is orthogonal to
![]() $\Gamma $
if and only if p is stably dominated if and only if p is generically stable. These other characterisations of orthogonality to
$\Gamma $
if and only if p is stably dominated if and only if p is generically stable. These other characterisations of orthogonality to
![]() $\Gamma $
of an C-definable type will be used when needed.
$\Gamma $
of an C-definable type will be used when needed.
If
![]() $f\colon X\to Y$
is a C-definable map, then we have a map
$f\colon X\to Y$
is a C-definable map, then we have a map
![]() $\widehat {f}\colon \widehat {X}(C)\to \widehat {Y}(C)$
given by
$\widehat {f}\colon \widehat {X}(C)\to \widehat {Y}(C)$
given by
![]() $\widehat {f}(p)=f_*(p)$
. Indeed,
$\widehat {f}(p)=f_*(p)$
. Indeed,
![]() $f_*(p)$
is clearly an C-definable global type on Y, and for any definable
$f_*(p)$
is clearly an C-definable global type on Y, and for any definable
![]() $h\colon Y\to \Gamma $
, we have that
$h\colon Y\to \Gamma $
, we have that
![]() $h\circ f\colon X\to \Gamma $
is definable and
$h\circ f\colon X\to \Gamma $
is definable and
![]() $(h\circ f)_*(p)=h_*(f_*(p))$
is a global type concentrated on a point of
$(h\circ f)_*(p)=h_*(f_*(p))$
is a global type concentrated on a point of
![]() $\Gamma $
. However, there are more maps that one has to consider between the stable completions of definable sets. To introduce these maps, we need to introduce the pro-definable structure associated to the stable completion of a definable set.
$\Gamma $
. However, there are more maps that one has to consider between the stable completions of definable sets. To introduce these maps, we need to introduce the pro-definable structure associated to the stable completion of a definable set.
Let
![]() $\mathrm {Pro}(\mathrm {Def} _C)$
be the category of C-pro-definable sets: that is, the category whose objects are filtrant projective limits of functors
$\mathrm {Pro}(\mathrm {Def} _C)$
be the category of C-pro-definable sets: that is, the category whose objects are filtrant projective limits of functors
where
![]() $(X_i)_{i\in I}$
is a cofiltering system in
$(X_i)_{i\in I}$
is a cofiltering system in
![]() $\mathrm {Def}_C$
indexed by a small, directed, partially ordered set, and the morphisms are the natural transformations of such functors. By a result of Kamensky [Reference Kamensky38], the functor of ‘taking
$\mathrm {Def}_C$
indexed by a small, directed, partially ordered set, and the morphisms are the natural transformations of such functors. By a result of Kamensky [Reference Kamensky38], the functor of ‘taking
![]() $\mathbb {U}$
-points’ induces an equivalence of categories between the category
$\mathbb {U}$
-points’ induces an equivalence of categories between the category
![]() $\mathrm {Pro}(\mathrm {Def}_C)$
and the subcategory of the category of sets whose objects and morphisms are projective limits of
$\mathrm {Pro}(\mathrm {Def}_C)$
and the subcategory of the category of sets whose objects and morphisms are projective limits of
![]() $\mathbb {U}$
-points of definable sets indexed by a small directed partially ordered set. So one can identify a pro-definable set X represented by
$\mathbb {U}$
-points of definable sets indexed by a small directed partially ordered set. So one can identify a pro-definable set X represented by
![]() $(X_i)_{i\in I}$
with
$(X_i)_{i\in I}$
with
![]() $X(\mathbb {U})=\underset {i}{\underleftarrow {\lim }} X_i(\mathbb {U})$
.
$X(\mathbb {U})=\underset {i}{\underleftarrow {\lim }} X_i(\mathbb {U})$
.
The sets of morphisms are related by
and we call the elements of
![]() $\mathrm {Hom}_{\mathrm {Pro}(\mathrm {Def}_C)}(X,Y)$
the C-pro-definable morphisms between X and Y.
$\mathrm {Hom}_{\mathrm {Pro}(\mathrm {Def}_C)}(X,Y)$
the C-pro-definable morphisms between X and Y.
Below, by strict C-pro-definable set, we mean a C-pro-definable set X for which there is a cofiltering system
![]() $(X_i)_{i\in I}$
in
$(X_i)_{i\in I}$
in
![]() $\mathrm {Def}_C$
representing X with the transition maps
$\mathrm {Def}_C$
representing X with the transition maps
![]() $\pi _{i,i'}\colon X_i\to X_{i'}$
being surjective for all
$\pi _{i,i'}\colon X_i\to X_{i'}$
being surjective for all
![]() $i\geq i'$
in
$i\geq i'$
in
![]() $I,$
or equivalently, with the C-pro-definable projection maps
$I,$
or equivalently, with the C-pro-definable projection maps
![]() $\pi _{i}\colon X\to X_i,$
represented by the transition maps
$\pi _{i}\colon X\to X_i,$
represented by the transition maps
![]() $\pi _{i,i'}\colon X_i\to X_{i'}$
for all
$\pi _{i,i'}\colon X_i\to X_{i'}$
for all
![]() $i\geq i',$
being surjective for all
$i\geq i',$
being surjective for all
![]() $i\in I$
.
$i\in I$
.
Fact 5.7 [Reference Hrushovski and Loeser35, Theorem 3.1.1] or [Reference Cubides Kovacsics and Ye16, Theorem 6.4].
For every C-definable set X, there is a canonical strict C-pro-definable set E and a canonical identification
![]() $\widehat {X}(F)=E(F)$
for every substructure F containing C. Moreover, if
$\widehat {X}(F)=E(F)$
for every substructure F containing C. Moreover, if
![]() $f\colon X\to Y$
is a morphism in
$f\colon X\to Y$
is a morphism in
![]() $\mathrm {Def} _C,$
then the induced map
$\mathrm {Def} _C,$
then the induced map
![]() $\widehat {f}\colon \widehat {X}(F)\to \widehat {Y}(F)$
is a morphism of C-pro-definable sets.
$\widehat {f}\colon \widehat {X}(F)\to \widehat {Y}(F)$
is a morphism of C-pro-definable sets.
![]() $\Box $
$\Box $
Thus we have a category
whose objects are of the form
![]() $\widehat {X}(C)$
for X a C-definable set and whose morphisms are the C-pro-definable morphisms between such objects. Furthermore, for every substructure F containing C, we have a functor
$\widehat {X}(C)$
for X a C-definable set and whose morphisms are the C-pro-definable morphisms between such objects. Furthermore, for every substructure F containing C, we have a functor
 $$ \begin{align*} \mathrm{Def} _C\to \widehat{\mathrm{Def}} _F \\[3pt] X\mapsto \widehat{X}(F). \end{align*} $$
$$ \begin{align*} \mathrm{Def} _C\to \widehat{\mathrm{Def}} _F \\[3pt] X\mapsto \widehat{X}(F). \end{align*} $$
Example 5.8 (The stable completion of the affine line).
Let K be a small elementary substructure of
![]() $\mathbb {U}$
. Let us describe the stable completion
$\mathbb {U}$
. Let us describe the stable completion
![]() $\widehat {\mathbb {A} ^1}(K)$
of the affine line. Let
$\widehat {\mathbb {A} ^1}(K)$
of the affine line. Let
![]() $\eta _{{\mathcal {R}}}$
denote the generic type of the valuation ring
$\eta _{{\mathcal {R}}}$
denote the generic type of the valuation ring
![]() ${\mathcal {R}}$
: that is, the global type in
${\mathcal {R}}$
: that is, the global type in
![]() $S_x(\mathbb {U})$
, where
$S_x(\mathbb {U})$
, where
![]() $|x|=1,$
determined by the following rule: a definable set
$|x|=1,$
determined by the following rule: a definable set
![]() $X\subseteq \mathbb {U}$
is in
$X\subseteq \mathbb {U}$
is in
![]() $\eta _{{\mathcal {R}}}$
if and only if there is
$\eta _{{\mathcal {R}}}$
if and only if there is
![]() $m\geq 1$
, and there are
$m\geq 1$
, and there are
![]() $b_1,\ldots ,b_m\in {\mathcal {R}}(K)$
such that
$b_1,\ldots ,b_m\in {\mathcal {R}}(K)$
such that
![]() $\mathrm {val} (b_i-b_j)=0$
for all
$\mathrm {val} (b_i-b_j)=0$
for all
![]() $i\neq j$
and
$i\neq j$
and
 $$\begin{align*}{\mathcal{R}}\setminus (\bigcup_{i=1}^m b_i+{\mathcal{M}}) \subseteq X. \end{align*}$$
$$\begin{align*}{\mathcal{R}}\setminus (\bigcup_{i=1}^m b_i+{\mathcal{M}}) \subseteq X. \end{align*}$$
By quantifier elimination and first-order logic compactness, for every formula
![]() $\phi (x,y)$
there is an integer
$\phi (x,y)$
there is an integer
![]() $m_{\phi }$
such that for all
$m_{\phi }$
such that for all
![]() $t\in \mathbb {U}^{|y|}$
, if
$t\in \mathbb {U}^{|y|}$
, if
![]() $X_t$
is defined by
$X_t$
is defined by
![]() $\phi (x,t)$
, then for all
$\phi (x,t)$
, then for all
![]() $m>m_{\phi }$
and all
$m>m_{\phi }$
and all
![]() $b_1,\ldots ,b_m\in {\mathcal {R}}(K)$
such that
$b_1,\ldots ,b_m\in {\mathcal {R}}(K)$
such that
![]() $\mathrm {val} (b_i-b_j)=0$
for all
$\mathrm {val} (b_i-b_j)=0$
for all
![]() $i\neq j$
, we have
$i\neq j$
, we have
 $$\begin{align*}{\mathcal{R}}\setminus (\bigcup_{i=1}^m b_i+{\mathcal{M}}) \not\subseteq X_t. \end{align*}$$
$$\begin{align*}{\mathcal{R}}\setminus (\bigcup_{i=1}^m b_i+{\mathcal{M}}) \not\subseteq X_t. \end{align*}$$
Therefore,
![]() $\eta _{{\mathcal {R}}}$
is a
$\eta _{{\mathcal {R}}}$
is a
![]() $\emptyset $
-definable global type (see also [Reference Haskell, Hrushovski and Macpherson32, Lemma 2.3.8]). We let the reader convince her/himself that
$\emptyset $
-definable global type (see also [Reference Haskell, Hrushovski and Macpherson32, Lemma 2.3.8]). We let the reader convince her/himself that
![]() $\eta _{{\mathcal {R}}}$
is orthogonal to
$\eta _{{\mathcal {R}}}$
is orthogonal to
![]() ${\Gamma }$
(see [Reference Haskell, Hrushovski and Macpherson32, Lemma 2.5.5]).
${\Gamma }$
(see [Reference Haskell, Hrushovski and Macpherson32, Lemma 2.5.5]).
Given any closed ball
centred at
![]() $a\in K$
with radius
$a\in K$
with radius
![]() $\gamma \in {\Gamma _{\infty } }(K)$
, by moving the centre and rescaling, there is a K-affine transformation f such that
$\gamma \in {\Gamma _{\infty } }(K)$
, by moving the centre and rescaling, there is a K-affine transformation f such that
![]() $f({\mathcal {R}})=B(a,\gamma )$
. We set
$f({\mathcal {R}})=B(a,\gamma )$
. We set
![]() $\eta _{B(a,\gamma )}=f_*(\eta _{{\mathcal {R}}})$
, and we call it the generic type of the closed ball
$\eta _{B(a,\gamma )}=f_*(\eta _{{\mathcal {R}}})$
, and we call it the generic type of the closed ball
![]() $B(a,\gamma )$
. Thus
$B(a,\gamma )$
. Thus
![]() $\eta _{B(a,\gamma )}$
is orthogonal to
$\eta _{B(a,\gamma )}$
is orthogonal to
![]() $\Gamma $
. Furthermore, it follows from [Reference Haskell, Hrushovski and Macpherson32, Lemma 2.3.3] that we have
$\Gamma $
. Furthermore, it follows from [Reference Haskell, Hrushovski and Macpherson32, Lemma 2.3.3] that we have
where
![]() $B(a,\infty ),$
the closed ball with radius
$B(a,\infty ),$
the closed ball with radius
![]() $\infty $
centred at
$\infty $
centred at
![]() $a,$
is identified with a.
$a,$
is identified with a.
As a set,
![]() $\widehat {\mathbb {P} ^1}(K)$
consists of the disjoint union of
$\widehat {\mathbb {P} ^1}(K)$
consists of the disjoint union of
![]() $\widehat {\mathbb {A}^1}(K)$
and the definable type concentrating on the point at infinity in
$\widehat {\mathbb {A}^1}(K)$
and the definable type concentrating on the point at infinity in
![]() $\mathbb {P}^1(K)$
. The description of
$\mathbb {P}^1(K)$
. The description of
![]() $\widehat {\mathbb {A} ^n}(K)$
for
$\widehat {\mathbb {A} ^n}(K)$
for
![]() $n>1$
is more complicated (see [Reference Hrushovski and Loeser35, Example 3.2.3]).
$n>1$
is more complicated (see [Reference Hrushovski and Loeser35, Example 3.2.3]).
Remark 5.9. Let K be an elementary substructure of
![]() $\mathbb {U}$
and X a K-definable set. Note that
$\mathbb {U}$
and X a K-definable set. Note that
![]() $\widehat {X}$
is a functor from the category of all elementary extensions of K into the category of sets (sending an elementary extension
$\widehat {X}$
is a functor from the category of all elementary extensions of K into the category of sets (sending an elementary extension
![]() $K'$
to
$K'$
to
![]() $\widehat {X}(K')$
). As for definable sets, the category of such functors is equivalent to the category of pro-definable sets of the form
$\widehat {X}(K')$
). As for definable sets, the category of such functors is equivalent to the category of pro-definable sets of the form
![]() $\widehat {X}(\mathbb {U})$
of all global definable types concentrating on X that are orthogonal to
$\widehat {X}(\mathbb {U})$
of all global definable types concentrating on X that are orthogonal to
![]() $\Gamma $
. From now on, unless otherwise stated, we will work with
$\Gamma $
. From now on, unless otherwise stated, we will work with
![]() $\widehat {X}$
, but all the definitions (respectively, results) still make sense (respectively, hold) also for
$\widehat {X}$
, but all the definitions (respectively, results) still make sense (respectively, hold) also for
![]() $\widehat {X}(K)$
. When we have two small elementary substructures K and
$\widehat {X}(K)$
. When we have two small elementary substructures K and
![]() $K'$
of
$K'$
of
![]() $\mathbb {U}$
, then we will use the notation
$\mathbb {U}$
, then we will use the notation
![]() $\widehat {X}(K)$
and
$\widehat {X}(K)$
and
![]() $\widehat {X}(K')$
to avoid ambiguity.
$\widehat {X}(K')$
to avoid ambiguity.
Let V be an algebraic variety, and let
![]() ${\mathcal {O}}_V$
be the sheaf of regular functions on V. Let
${\mathcal {O}}_V$
be the sheaf of regular functions on V. Let
![]() $\mathcal {O}_V^{\mathrm {val}}$
be the sheaf of
$\mathcal {O}_V^{\mathrm {val}}$
be the sheaf of
![]() ${\Gamma _{\infty } }$
-valued functions defined by
${\Gamma _{\infty } }$
-valued functions defined by
for
![]() $U\subseteq V$
a Zariski open subset. The topology on the stable completion
$U\subseteq V$
a Zariski open subset. The topology on the stable completion
![]() $\widehat {V}$
is the topology having as a basis finite unions of finite intersections of sets of the following form:
$\widehat {V}$
is the topology having as a basis finite unions of finite intersections of sets of the following form:
where U is a Zariski open set of V,
![]() $f\in {\mathcal {O}}_V^{\mathrm {val}}(U)$
and I is an open interval on
$f\in {\mathcal {O}}_V^{\mathrm {val}}(U)$
and I is an open interval on
![]() ${\Gamma _{\infty } }$
.
${\Gamma _{\infty } }$
.
![]() $\widehat {V\times {\Gamma ^n_{\infty } }}$
is equipped with the quotient topology induced by the map
$\widehat {V\times {\Gamma ^n_{\infty } }}$
is equipped with the quotient topology induced by the map
and, for a definable subset
![]() $X\subseteq V\times {\Gamma ^m_{\infty } }$
, we put on
$X\subseteq V\times {\Gamma ^m_{\infty } }$
, we put on
![]() $\widehat {X}$
the induced topology from
$\widehat {X}$
the induced topology from
![]() $\widehat {V\times {\Gamma ^m_{\infty } }}$
.
$\widehat {V\times {\Gamma ^m_{\infty } }}$
.
By [Reference Hrushovski and Loeser35, Lemma 3.5.3], we have:
Fact 5.10. If
![]() $Y\subseteq {\Gamma ^m_{\infty } }$
is a definable subset, then
$Y\subseteq {\Gamma ^m_{\infty } }$
is a definable subset, then
![]() $\widehat {Y}=Y$
. The topology on
$\widehat {Y}=Y$
. The topology on
![]() $\widehat {{\Gamma _{\infty } }}= {\Gamma _{\infty } }$
coincides with the order topology on
$\widehat {{\Gamma _{\infty } }}= {\Gamma _{\infty } }$
coincides with the order topology on
![]() ${\Gamma _{\infty } }$
, and the topology on
${\Gamma _{\infty } }$
, and the topology on
![]() $\widehat {{\Gamma ^n_{\infty } }}= {\Gamma ^n_{\infty } }$
is the product topology.
$\widehat {{\Gamma ^n_{\infty } }}= {\Gamma ^n_{\infty } }$
is the product topology.
If X is a definable subset of an algebraic variety
![]() $V,$
then there is a canonical bijection from
$V,$
then there is a canonical bijection from
![]() $\widehat {X}\times Y$
to
$\widehat {X}\times Y$
to
![]() $\widehat {X\times Y}$
such that the topology on
$\widehat {X\times Y}$
such that the topology on
![]() $\widehat {X\times Y}=\widehat {X}\times Y$
is the product topology.
$\widehat {X\times Y}=\widehat {X}\times Y$
is the product topology.
![]() $\Box $
$\Box $
By [Reference Hrushovski and Loeser35, Proposition 4.2.21 and Corollary 4.2.22], the topology on the stable completion is related to the
![]() $\mathrm {v\!+\!g}$
-site by:
$\mathrm {v\!+\!g}$
-site by:
Fact 5.11. Let V be an algebraic variety over K, and let W be a definable subset of
![]() $V\times {\Gamma ^m_{\infty } }$
. Then W is
$V\times {\Gamma ^m_{\infty } }$
. Then W is
![]() $\mathrm {v\!+\!g}$
-open (respectively,
$\mathrm {v\!+\!g}$
-open (respectively,
![]() $\mathrm {v\!+\!g}$
-closed) if and only if
$\mathrm {v\!+\!g}$
-closed) if and only if
![]() $\widehat {W}$
is open (respectively, closed) in
$\widehat {W}$
is open (respectively, closed) in
![]() $\widehat {V}\times {\Gamma ^m_{\infty } }$
. Moreover, a basis for the topology on the stable completion
$\widehat {V}\times {\Gamma ^m_{\infty } }$
. Moreover, a basis for the topology on the stable completion
![]() $\widehat {X}$
of a definable subset of
$\widehat {X}$
of a definable subset of
![]() $V\times {\Gamma ^m_{\infty } }$
is given by
$V\times {\Gamma ^m_{\infty } }$
is given by
□
As we pointed out already, in general, the stable completion topology is not necessarily locally compact:
Remark 5.12 (The stable completion topology and local compactness).
Consider the affine line over
![]() $\mathbb {C}_p$
(the completion of the algebraic closure of
$\mathbb {C}_p$
(the completion of the algebraic closure of
![]() $\mathbb {Q} _p$
). The space
$\mathbb {Q} _p$
). The space
![]() $\widehat {\mathbb {A} ^1}(\mathbb {C}_p)$
is not locally compact. Indeed, suppose for a contradiction there is a compact neighbourhood U of
$\widehat {\mathbb {A} ^1}(\mathbb {C}_p)$
is not locally compact. Indeed, suppose for a contradiction there is a compact neighbourhood U of
![]() $\eta _{{\mathcal {R}}}$
, the generic type of the valuation ring (the Gauss point). Then there is
$\eta _{{\mathcal {R}}}$
, the generic type of the valuation ring (the Gauss point). Then there is
![]() $I\subseteq \mathbb {Q}$
an open interval such that
$I\subseteq \mathbb {Q}$
an open interval such that
![]() $\widehat {\mathrm {val} }^{-1}(I)\subseteq U$
. Let
$\widehat {\mathrm {val} }^{-1}(I)\subseteq U$
. Let
![]() $J\subseteq I$
be a closed sub-interval. Then by continuity of
$J\subseteq I$
be a closed sub-interval. Then by continuity of
![]() $\widehat {\mathrm {val}}$
,
$\widehat {\mathrm {val}}$
,
![]() $\widehat {\mathrm {val}}^{-1}(J)$
is a closed subset of U and hence a compact subset. Therefore, its image J would be a compact subset of
$\widehat {\mathrm {val}}^{-1}(J)$
is a closed subset of U and hence a compact subset. Therefore, its image J would be a compact subset of
![]() $\mathbb {Q}$
.
$\mathbb {Q}$
.
Due to the failure of local compactness of the stable completion’s topology, in order to develop a cohomology theory in the category of stable completions of definable sets, we will replace the stable completion’s topology by a site:
Definition 5.13 (
 $\widehat {\mathrm {v\!+\!g}}$
-site on stable completions).
$\widehat {\mathrm {v\!+\!g}}$
-site on stable completions).
If
![]() $X\subseteq V\times {\Gamma ^m_{\infty } }$
is a definable subset, the
$X\subseteq V\times {\Gamma ^m_{\infty } }$
is a definable subset, the
![]() $\widehat {\mathrm {v\!+\!g}}$
-site on
$\widehat {\mathrm {v\!+\!g}}$
-site on
![]() $\widehat {X}$
, denoted
$\widehat {X}$
, denoted
![]() $\widehat {X}_{\widehat {\mathrm {v\!+\!g}}},$
is the category
$\widehat {X}_{\widehat {\mathrm {v\!+\!g}}},$
is the category
![]() $\mathrm {Op}(\widehat {X}_{\widehat {\mathrm {v\!+\!g}}})$
whose objects are of the form
$\mathrm {Op}(\widehat {X}_{\widehat {\mathrm {v\!+\!g}}})$
whose objects are of the form
![]() $\widehat {W}$
with
$\widehat {W}$
with
![]() $W\in \mathrm {Op}(X_{\mathrm {v\!+\!g}}),$
the morphisms are the inclusions, and the admissible covers
$W\in \mathrm {Op}(X_{\mathrm {v\!+\!g}}),$
the morphisms are the inclusions, and the admissible covers
![]() $\mathrm {Cov}(\widehat {U})$
of
$\mathrm {Cov}(\widehat {U})$
of
![]() $\widehat {U}\in \mathrm {Op} (\widehat {X}_{\widehat {\mathrm {v\!+\!g}}})$
are covers by objects of
$\widehat {U}\in \mathrm {Op} (\widehat {X}_{\widehat {\mathrm {v\!+\!g}}})$
are covers by objects of
![]() $\mathrm {Op} (\widehat {X}_{\widehat {\mathrm {v\!+\!g}}})$
with finite subcovers.
$\mathrm {Op} (\widehat {X}_{\widehat {\mathrm {v\!+\!g}}})$
with finite subcovers.
Of course, the
![]() $\mathrm {v\!+\!g}$
-site
$\mathrm {v\!+\!g}$
-site
![]() $X_{\mathrm {v\!+\!g}}$
on a definable set X and the
$X_{\mathrm {v\!+\!g}}$
on a definable set X and the
![]() $\widehat {\mathrm {v\!+\!g}}$
-site
$\widehat {\mathrm {v\!+\!g}}$
-site
![]() $\widehat {X}_{\widehat {\mathrm {v\!+\!g}}}$
on its stable completion are isomorphic categories, so we will often move from one site to the other whenever convenient.
$\widehat {X}_{\widehat {\mathrm {v\!+\!g}}}$
on its stable completion are isomorphic categories, so we will often move from one site to the other whenever convenient.
5.3 The
 $\widehat {\mathrm {v\!+\!g}}$
-site and
$\widehat {\mathrm {v\!+\!g}}$
-site and
 ${\mathcal {T}}$
-spaces
${\mathcal {T}}$
-spaces
Here we show that the stable completion of a definable subset of
![]() $V\times {\Gamma ^n_{\infty } }$
equipped with the
$V\times {\Gamma ^n_{\infty } }$
equipped with the
![]() $\widehat {\mathrm {v\!+\!g}}$
-site is a
$\widehat {\mathrm {v\!+\!g}}$
-site is a
![]() ${\mathcal {T}}$
-space. For that, we use the following special case of Hrushovski and Loeser’s main theorem:
${\mathcal {T}}$
-space. For that, we use the following special case of Hrushovski and Loeser’s main theorem:
Fact 5.14 [Reference Hrushovski and Loeser35, Theorem 11.1.1].
Let V be a quasi-projective variety over K, and let X be a definable subset of
![]() $V\times {\Gamma ^n_{\infty } }$
. Then there exists a (continuous) pro-definable deformation retraction
$V\times {\Gamma ^n_{\infty } }$
. Then there exists a (continuous) pro-definable deformation retraction
![]() $H\colon I\times \widehat {X}\to \widehat {X}$
with image
$H\colon I\times \widehat {X}\to \widehat {X}$
with image
![]() ${\mathfrak X}$
an iso-definable subset definably homeomorphic to a definable subset of some
${\mathfrak X}$
an iso-definable subset definably homeomorphic to a definable subset of some
![]() ${\Gamma ^k_{\infty } }$
. Furthermore, given finitely many definable subsets
${\Gamma ^k_{\infty } }$
. Furthermore, given finitely many definable subsets
![]() $X_1, \ldots , X_n$
of X, the pro-definable deformation retraction H can be constructed preserving each of the definable subsets: that is, the restriction
$X_1, \ldots , X_n$
of X, the pro-definable deformation retraction H can be constructed preserving each of the definable subsets: that is, the restriction
![]() $H_{|}:I\times \widehat {X_i}\to \widehat {X_i}$
is still a continuous pro-definable retraction.
$H_{|}:I\times \widehat {X_i}\to \widehat {X_i}$
is still a continuous pro-definable retraction.
![]() $\Box $
$\Box $
The I in the theorem is a generalised interval: that is, a one-dimensional
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable space obtained by considering finitely many oriented closed sub-intervals of
${\mathbf {\Gamma }_{\infty } }$
-definable space obtained by considering finitely many oriented closed sub-intervals of
![]() ${\Gamma _{\infty } }$
and glueing them together two by two, end to end, respecting the orientations. The set
${\Gamma _{\infty } }$
and glueing them together two by two, end to end, respecting the orientations. The set
![]() ${\mathfrak X}$
is called a skeleton of
${\mathfrak X}$
is called a skeleton of
![]() $\widehat {X}$
and is often identified, under the definable homeomorphism, with a definable subset of
$\widehat {X}$
and is often identified, under the definable homeomorphism, with a definable subset of
![]() ${\Gamma ^k_{\infty } }$
.
${\Gamma ^k_{\infty } }$
.
Also recall ([Reference Hrushovski and Loeser35, Definition 2.2.2]) that if X is a pro-definable set, then Z is a pro-definable subset of X if and only if there are cofiltering systems of definable sets
![]() $(X_i)_{i\in I}$
and
$(X_i)_{i\in I}$
and
![]() $(Z_i)_{i\in I}$
representing X and Z, respectively, such that for each i,
$(Z_i)_{i\in I}$
representing X and Z, respectively, such that for each i,
![]() $Z_i\subseteq X_i$
and for all
$Z_i\subseteq X_i$
and for all
![]() $i\geq i'$
the transition maps
$i\geq i'$
the transition maps
![]() $Z_i\to Z_{i'}$
are the restrictions of the transitions maps
$Z_i\to Z_{i'}$
are the restrictions of the transitions maps
![]() $X_i\to X_{i'};$
we say that Z is an iso-definable subset of X if furthermore there is
$X_i\to X_{i'};$
we say that Z is an iso-definable subset of X if furthermore there is
![]() $i_0$
such that restriction maps
$i_0$
such that restriction maps
![]() $Z_i\to Z_{i'}$
are bijections for all
$Z_i\to Z_{i'}$
are bijections for all
![]() $i\geq i'\geq i_0,$
or equivalently, the projection maps
$i\geq i'\geq i_0,$
or equivalently, the projection maps
![]() $Z\to Z_i$
are bijections for all
$Z\to Z_i$
are bijections for all
![]() $i\geq i_0$
.
$i\geq i_0$
.
Let X be a pro-definable set. A pro-definable subset Y of X is said to be relatively definable if for some cofiltering system
![]() $(X_i)_{i\in I}$
of definable sets representing
$(X_i)_{i\in I}$
of definable sets representing
![]() $X,$
with transitions
$X,$
with transitions
![]() $\pi _{i,i'}\colon X_i\to X_{i'}$
for all
$\pi _{i,i'}\colon X_i\to X_{i'}$
for all
![]() $i\geq i'$
in
$i\geq i'$
in
![]() $I,$
there is
$I,$
there is
![]() $i_0\in I$
and a definable subset
$i_0\in I$
and a definable subset
![]() $Y_{i_0}\subseteq X_{i_0}$
such that
$Y_{i_0}\subseteq X_{i_0}$
such that
![]() $(Y_i)_{i\geq i_0}$
, where
$(Y_i)_{i\geq i_0}$
, where
![]() $Y_i=\pi _{i,i_0}^{-1}(Y_{i_0})$
represents Y or, equivalently,
$Y_i=\pi _{i,i_0}^{-1}(Y_{i_0})$
represents Y or, equivalently,
![]() $Y=\pi _{i_0}^{-1}(Y_{i_0})$
, where
$Y=\pi _{i_0}^{-1}(Y_{i_0})$
, where
![]() $\pi _{i_0}\colon X\to X_{i_0}$
denotes the natural (pro-definable) projection map represented by the transition maps
$\pi _{i_0}\colon X\to X_{i_0}$
denotes the natural (pro-definable) projection map represented by the transition maps
![]() $\pi _{i,i_0}\colon X_i\to X_{i_0}$
for all
$\pi _{i,i_0}\colon X_i\to X_{i_0}$
for all
![]() $i\geq i_0$
.
$i\geq i_0$
.
The main examples of relatively definable subsets are obtained when we have
![]() $W\subseteq X\subseteq V\times {\Gamma ^m_{\infty } }$
are definable sets, since by construction of the pro-definable structure on the stable completions,
$W\subseteq X\subseteq V\times {\Gamma ^m_{\infty } }$
are definable sets, since by construction of the pro-definable structure on the stable completions,
![]() $\widehat {W}$
is a relatively definable subset of
$\widehat {W}$
is a relatively definable subset of
![]() $\widehat {X}$
. The following gives another kind of example that we require below:
$\widehat {X}$
. The following gives another kind of example that we require below:
Remark 5.15 (Simple points).
Given
![]() $X\subseteq V\times {\Gamma ^m_{\infty } }$
a definable subset, there is a canonical embedding
$X\subseteq V\times {\Gamma ^m_{\infty } }$
a definable subset, there is a canonical embedding
![]() $\iota _X\colon X\to \widehat {X},$
taking a point a to the global type
$\iota _X\colon X\to \widehat {X},$
taking a point a to the global type
![]() $\mathrm {tp} (a/\mathbb {U})$
concentrating on a. The points of the image are called the simple points of
$\mathrm {tp} (a/\mathbb {U})$
concentrating on a. The points of the image are called the simple points of
![]() $\widehat {X}$
, and the set
$\widehat {X}$
, and the set
![]() $\iota _X(X)$
will be denoted by
$\iota _X(X)$
will be denoted by
![]() $\widehat {X}_s$
. Note that
$\widehat {X}_s$
. Note that
![]() $\iota _X\colon X \to \widehat {X}_s$
is a pro-definable bijection. By working on affine charts and using the fact that the induced topology from
$\iota _X\colon X \to \widehat {X}_s$
is a pro-definable bijection. By working on affine charts and using the fact that the induced topology from
![]() $\widehat {V\times \Gamma _{\infty }^m}=\widehat {V}\times \Gamma _{\infty }^m$
on
$\widehat {V\times \Gamma _{\infty }^m}=\widehat {V}\times \Gamma _{\infty }^m$
on
![]() $V\times \Gamma _{\infty }^m$
via
$V\times \Gamma _{\infty }^m$
via
![]() $\iota _{V\times \Gamma _{\infty }^m}^{-1}$
coincides with the product topology between the valuation topology on V and the (product) order topology on
$\iota _{V\times \Gamma _{\infty }^m}^{-1}$
coincides with the product topology between the valuation topology on V and the (product) order topology on
![]() $\Gamma _{\infty }^m,$
we see that [Reference Hrushovski and Loeser35, Lemma 3.6.1] can also be extended to definable subsets of
$\Gamma _{\infty }^m,$
we see that [Reference Hrushovski and Loeser35, Lemma 3.6.1] can also be extended to definable subsets of
![]() $V\times {\Gamma ^m_{\infty } }:$
$V\times {\Gamma ^m_{\infty } }:$
-
• The set
 $\widehat {X}_s$
of simple points of
$\widehat {X}_s$
of simple points of
 $\widehat {X}$
is a dense, iso-definable and relatively definable subset of
$\widehat {X}$
is a dense, iso-definable and relatively definable subset of
 $\widehat {X}$
.
$\widehat {X}$
.
Lemma 5.16. Let X be a pro-definable set, Z be a strict pro-definable subset of X and W be an iso-definable subset of X. Then:
-
(a) If Y is a relatively definable subset of X, then
 $Y\cap Z$
is strict pro-definable.
$Y\cap Z$
is strict pro-definable. -
(b) If Y is an iso-definable and relatively definable subset of X, then
 $Y\cap Z$
is iso-definable.
$Y\cap Z$
is iso-definable. -
(c) If Y is a relatively definable subset of X, then
 $Y\cap W$
is iso-definable.
$Y\cap W$
is iso-definable.
Proof. Suppose that
![]() $(X_i)_{i\in I}$
is a cofiltering system of definable sets representing
$(X_i)_{i\in I}$
is a cofiltering system of definable sets representing
![]() $X,$
with transitions
$X,$
with transitions
![]() $\pi _{i,i'}\colon X_i\to X_{i'}$
for all
$\pi _{i,i'}\colon X_i\to X_{i'}$
for all
![]() $i\geq i'$
in I. Let
$i\geq i'$
in I. Let
![]() $i_0\in I$
be such that
$i_0\in I$
be such that
![]() $\pi _{i_0}^{-1}(Y_{i_0})=Y$
for
$\pi _{i_0}^{-1}(Y_{i_0})=Y$
for
![]() $Y_{i_0}$
a definable subset of
$Y_{i_0}$
a definable subset of
![]() $X_{i_0}$
, so that if for all
$X_{i_0}$
, so that if for all
![]() $i\geq i_0$
,
$i\geq i_0$
,
![]() $Y_i:= \pi _{i,i_0}^{-1}(Y_{i_0}),$
then Y is represented by
$Y_i:= \pi _{i,i_0}^{-1}(Y_{i_0}),$
then Y is represented by
![]() $(Y_i)_{i\geq i_0}$
. Without loss of generality, we may also suppose that if for all
$(Y_i)_{i\geq i_0}$
. Without loss of generality, we may also suppose that if for all
![]() $i\geq i_0, \ Z_i:= \pi _i(Z),$
then Z is represented by
$i\geq i_0, \ Z_i:= \pi _i(Z),$
then Z is represented by
![]() $(Z_i)_{i\geq i_0}$
and, if for all
$(Z_i)_{i\geq i_0}$
and, if for all
![]() $\geq i_0, \ W_i=\pi _i(Z)$
, then W is represented by
$\geq i_0, \ W_i=\pi _i(Z)$
, then W is represented by
![]() $(W_i)_{i\geq i_0}$
.
$(W_i)_{i\geq i_0}$
.
(a) We show that for all
![]() $i\geq i_0, \ \pi _i(Y\cap Z)=Y_i\cap Z_i$
. The inclusion from left to right is immediate. For the converse, let
$i\geq i_0, \ \pi _i(Y\cap Z)=Y_i\cap Z_i$
. The inclusion from left to right is immediate. For the converse, let
![]() $a\in Y_i\cap Z_i$
. By assumption, there is
$a\in Y_i\cap Z_i$
. By assumption, there is
![]() $x\in Z$
such that
$x\in Z$
such that
![]() $\pi _i(x)=a$
. Since Y is relatively definable,
$\pi _i(x)=a$
. Since Y is relatively definable,
![]() $\pi _i^{-1}(Y_i)=Y$
, so
$\pi _i^{-1}(Y_i)=Y$
, so
![]() $x\in Y$
, and therefore
$x\in Y$
, and therefore
![]() $a\in \pi _i(Y\cap Z)$
.
$a\in \pi _i(Y\cap Z)$
.
(b) It suffices to show that
![]() $Y\cap Z=Y\cap \pi _{i_0}^{-1}(Z_{i_0})$
, since the right-hand side set
$Y\cap Z=Y\cap \pi _{i_0}^{-1}(Z_{i_0})$
, since the right-hand side set
![]() $\pi _{i_0}^{-1}(Y_{i_0}\cap Z_{i_0}),$
being in pro-definable bijection under
$\pi _{i_0}^{-1}(Y_{i_0}\cap Z_{i_0}),$
being in pro-definable bijection under
![]() $\pi _{i_0}$
with a definable set, is iso-definable by [Reference Hrushovski and Loeser35, Corollary 2.2.4]. The left-to-right inclusion is clear. For the converse, suppose
$\pi _{i_0}$
with a definable set, is iso-definable by [Reference Hrushovski and Loeser35, Corollary 2.2.4]. The left-to-right inclusion is clear. For the converse, suppose
![]() $a\in Y$
and
$a\in Y$
and
![]() $\pi _{i_0}(a)\in Z_{i_0}$
. By surjectivity of
$\pi _{i_0}(a)\in Z_{i_0}$
. By surjectivity of
![]() $\pi _{i_0}\colon Z\to Z_{i_0},$
there is
$\pi _{i_0}\colon Z\to Z_{i_0},$
there is
![]() $b\in Z$
such that
$b\in Z$
such that
![]() $\pi _{i_0}(b)=\pi _{i_0}(a)\in Y_{i_0}$
. It follows that
$\pi _{i_0}(b)=\pi _{i_0}(a)\in Y_{i_0}$
. It follows that
![]() $b\in \pi _{i_0}^{-1}(Y_{i_0})=Y$
. Therefore, since
$b\in \pi _{i_0}^{-1}(Y_{i_0})=Y$
. Therefore, since
![]() $\pi _{i_0}\colon Y\to Y_{i_0}$
is a bijection,
$\pi _{i_0}\colon Y\to Y_{i_0}$
is a bijection,
![]() $a=b$
and
$a=b$
and
![]() $a\in Y\cap Z$
.
$a\in Y\cap Z$
.
(c) We have
![]() $\pi _{i_0}^{-1}(Y_{i_0}\cap W_{i_0})=\pi _{i_0}^{-1}(Y_{i_0})\cap \pi _{i_0}^{-1}(W_{i_0})=Y\cap W$
since
$\pi _{i_0}^{-1}(Y_{i_0}\cap W_{i_0})=\pi _{i_0}^{-1}(Y_{i_0})\cap \pi _{i_0}^{-1}(W_{i_0})=Y\cap W$
since
![]() $\pi _{i}:W\to W_i$
is a bijection for all
$\pi _{i}:W\to W_i$
is a bijection for all
![]() $i\geq i_0$
.
$i\geq i_0$
.
The following lemma is easy and left to the reader.
Lemma 5.17. Let X and Y be pro-definable sets and
![]() $f\colon X\to Y$
be a pro-definable map. If U is a relatively definable subset of
$f\colon X\to Y$
be a pro-definable map. If U is a relatively definable subset of
![]() $Y,$
then
$Y,$
then
![]() $f^{-1}(U)$
is a relatively definable subset of X.
$f^{-1}(U)$
is a relatively definable subset of X.
![]() $\Box $
$\Box $
There is a notion of definable connectedness in the stable completion introduced at the beginning of [Reference Hrushovski and Loeser35, Section 10.4]. Note that it is introduced there only for stable completions of definable subsets of an algebraic variety V over a valued field, but this notion can be extended to stable completions of definable subsets of
![]() $V\times {\Gamma ^m_{\infty } }$
in the following way:
$V\times {\Gamma ^m_{\infty } }$
in the following way:
Definition 5.18 (Definable connectedness in the stable completion).
Let V be an algebraic variety. A strict pro-definable subset Z of
![]() $\widehat {V}$
is definably connected if and only if the only strict pro-definable clopen subsets of Z are
$\widehat {V}$
is definably connected if and only if the only strict pro-definable clopen subsets of Z are
![]() $\emptyset $
and Z.
$\emptyset $
and Z.
If
![]() $X\subseteq V\times {\Gamma ^m_{\infty } }$
is a definable subset, we say that
$X\subseteq V\times {\Gamma ^m_{\infty } }$
is a definable subset, we say that
![]() $\widehat {X}$
is definably connected if and only if the pullback of
$\widehat {X}$
is definably connected if and only if the pullback of
![]() $\widehat {X}$
under
$\widehat {X}$
under
![]() $\widehat {\mathrm {id}\times \mathrm {val} }: \widehat {V\times \mathbb {A} ^m}\to \widehat {V\times {\Gamma ^m_{\infty } }}$
is definably connected.
$\widehat {\mathrm {id}\times \mathrm {val} }: \widehat {V\times \mathbb {A} ^m}\to \widehat {V\times {\Gamma ^m_{\infty } }}$
is definably connected.
We have the following characterisation of definable connectedness (slightly extending the observation at the beginning of [Reference Hrushovski and Loeser35, Section 10.4] for the case of definable subsets of V).
Lemma 5.19. Let V be an algebraic variety, and let X be a definable subset of
![]() $V\times {\Gamma ^m_{\infty } }$
. Then
$V\times {\Gamma ^m_{\infty } }$
. Then
![]() $\widehat {X}$
is definably connected if and only if the only
$\widehat {X}$
is definably connected if and only if the only
![]() $\mathrm {v\!+\!g}$
-clopen subsets of X are
$\mathrm {v\!+\!g}$
-clopen subsets of X are
![]() $\emptyset $
and X. In fact, the definably connected components of
$\emptyset $
and X. In fact, the definably connected components of
![]() $\widehat {X}$
are of the form
$\widehat {X}$
are of the form
![]() $\widehat {U}$
for some
$\widehat {U}$
for some
![]() $\mathrm {v\!+\!g}$
-clopen subset U of X such that
$\mathrm {v\!+\!g}$
-clopen subset U of X such that
![]() $\widehat {U}$
is definably connected.
$\widehat {U}$
is definably connected.
Proof. The left-to-right implication follows directly from Fact 5.11. For the converse, suppose that the only
![]() $\mathrm {v\!+\!g}$
-clopen subsets of X are
$\mathrm {v\!+\!g}$
-clopen subsets of X are
![]() $\emptyset $
and X, and assume for a contradiction that there is a proper strict pro-definable clopen subset U of
$\emptyset $
and X, and assume for a contradiction that there is a proper strict pro-definable clopen subset U of
![]() $\widehat {X}$
. By Remark 5.15 and Lemma 5.16(b), the set
$\widehat {X}$
. By Remark 5.15 and Lemma 5.16(b), the set
![]() $U\cap \widehat {X}_s$
is an iso-definable subset of
$U\cap \widehat {X}_s$
is an iso-definable subset of
![]() $\widehat {X}$
. Furthermore, by the density of
$\widehat {X}$
. Furthermore, by the density of
![]() $\widehat {X}_s$
in
$\widehat {X}_s$
in
![]() $\widehat {X}$
and the fact that U is clopen, we have
$\widehat {X}$
and the fact that U is clopen, we have
![]() $\mathrm {cl}(U\cap \widehat {X}_s)=U\cap \widehat {X}=U$
, where
$\mathrm {cl}(U\cap \widehat {X}_s)=U\cap \widehat {X}=U$
, where
![]() $\mathrm {cl}$
denotes the closure in
$\mathrm {cl}$
denotes the closure in
![]() $\widehat {X}$
. Abusing notation, let
$\widehat {X}$
. Abusing notation, let
![]() $U\cap X$
denote
$U\cap X$
denote
![]() $\iota _X^{-1}(U\cap \widehat {X}_s)$
. Since
$\iota _X^{-1}(U\cap \widehat {X}_s)$
. Since
![]() $\widehat {X}_s$
is iso-definable,
$\widehat {X}_s$
is iso-definable,
![]() $U\cap X$
is a definable subset of X.
$U\cap X$
is a definable subset of X.
Claim 5.20.
![]() $\widehat {U\cap X}=U$
.
$\widehat {U\cap X}=U$
.
Proof. First note that
![]() $(\widehat {U\cap X})_s= U\cap \widehat {X}_s$
. Indeed,
$(\widehat {U\cap X})_s= U\cap \widehat {X}_s$
. Indeed,
 $$ \begin{align*} p\in (\widehat{U\cap X)}_s & \Leftrightarrow \exists a\in U\cap X \text{ such that } p=\mathrm{tp}(a/\mathbb{U})\\ & \Leftrightarrow \exists a\in \iota_X^{-1}(U) \text{ such that } p=\mathrm{tp}(a/\mathbb{U})\\ & \Leftrightarrow p\in U\cap \widehat{X}_s. \end{align*} $$
$$ \begin{align*} p\in (\widehat{U\cap X)}_s & \Leftrightarrow \exists a\in U\cap X \text{ such that } p=\mathrm{tp}(a/\mathbb{U})\\ & \Leftrightarrow \exists a\in \iota_X^{-1}(U) \text{ such that } p=\mathrm{tp}(a/\mathbb{U})\\ & \Leftrightarrow p\in U\cap \widehat{X}_s. \end{align*} $$
By the density of simple points, this yields that
which shows that
![]() $\widehat {U\cap X}\subseteq U$
. For the converse inclusion, consider
$\widehat {U\cap X}\subseteq U$
. For the converse inclusion, consider
![]() $W:= \widehat {X}\setminus U$
. The set W is clopen, and
$W:= \widehat {X}\setminus U$
. The set W is clopen, and
![]() $W\cap \widehat {X}_s$
is also iso-definable since
$W\cap \widehat {X}_s$
is also iso-definable since
![]() $W\cap \widehat {X_s} = \widehat {X}_s\setminus U\cap \widehat {X}_s$
is in pro-definable bijection with the definable set
$W\cap \widehat {X_s} = \widehat {X}_s\setminus U\cap \widehat {X}_s$
is in pro-definable bijection with the definable set
![]() $X\setminus U\cap X$
. Let
$X\setminus U\cap X$
. Let
![]() $W\cap X$
denote
$W\cap X$
denote
![]() $\iota _X^{-1}(W\cap \widehat {X}_s)$
. Then the sets
$\iota _X^{-1}(W\cap \widehat {X}_s)$
. Then the sets
![]() $W\cap X$
and
$W\cap X$
and
![]() $U\cap X$
form a definable partition of X. By the same argument above,
$U\cap X$
form a definable partition of X. By the same argument above,
![]() $\widehat {W\cap X}\subseteq W$
. This shows the converse inclusion: if there were
$\widehat {W\cap X}\subseteq W$
. This shows the converse inclusion: if there were
![]() $x\in U\setminus \widehat {U\cap X}$
, since
$x\in U\setminus \widehat {U\cap X}$
, since
![]() $\widehat {X}=\widehat {U\cap X}\cup \widehat {W\cap X}$
, we must have that
$\widehat {X}=\widehat {U\cap X}\cup \widehat {W\cap X}$
, we must have that
![]() $x\in \widehat {W\cap X}$
, which implies
$x\in \widehat {W\cap X}$
, which implies
![]() $x\in W$
, a contradiction.
$x\in W$
, a contradiction.
The claim, together with Fact 5.11, contradicts the assumption on X.
A first consequence of Fact 5.14 is the following:
Lemma 5.21. Let V be an algebraic variety, and let
![]() $X \subseteq V\times {\Gamma ^n_{\infty } }$
be a definable set. Then
$X \subseteq V\times {\Gamma ^n_{\infty } }$
be a definable set. Then
![]() $\widehat {X}$
has finitely many definably connected components.
$\widehat {X}$
has finitely many definably connected components.
Proof. Suppose that V is quasi-projective. Then by Fact 5.14, let
![]() $H\colon I\times \widehat {X}\to \widehat {X}$
be a continuous pro-definable deformation retraction with image an iso-definable subset
$H\colon I\times \widehat {X}\to \widehat {X}$
be a continuous pro-definable deformation retraction with image an iso-definable subset
![]() ${\mathfrak X}$
of
${\mathfrak X}$
of
![]() $\widehat {X}$
, and let
$\widehat {X}$
, and let
![]() $h\colon {\mathfrak X}\to {\mathcal X}$
be a pro-definable homeomorphism of
$h\colon {\mathfrak X}\to {\mathcal X}$
be a pro-definable homeomorphism of
![]() ${\mathfrak X}$
with a definable subset
${\mathfrak X}$
with a definable subset
![]() ${\mathcal X}$
of
${\mathcal X}$
of
![]() ${\Gamma ^k_{\infty } }$
. Let also
${\Gamma ^k_{\infty } }$
. Let also
![]() $i_I, e_I\in I$
be the initial and last end points of I. Let
$i_I, e_I\in I$
be the initial and last end points of I. Let
![]() $f\colon \widehat {X}\to {\mathfrak X}$
and
$f\colon \widehat {X}\to {\mathfrak X}$
and
![]() $g\colon \widehat {X}\to {\mathcal X}$
be the continuous pro-definable maps given by
$g\colon \widehat {X}\to {\mathcal X}$
be the continuous pro-definable maps given by
![]() $f(x)=H(e_I, x)$
and
$f(x)=H(e_I, x)$
and
![]() $g=h\circ f$
.
$g=h\circ f$
.
Since definable subsets of
![]() ${\Gamma ^k_{\infty } }$
have finitely many definably connected components, let
${\Gamma ^k_{\infty } }$
have finitely many definably connected components, let
![]() ${\mathcal X}_1, \ldots , {\mathcal X}_k$
be the finitely many definably connected components of
${\mathcal X}_1, \ldots , {\mathcal X}_k$
be the finitely many definably connected components of
![]() ${\mathcal X}$
. Let
${\mathcal X}$
. Let
![]() ${\mathfrak X}_1, \ldots , {\mathfrak X}_k$
be the corresponding (under h) finitely many definably connected components of
${\mathfrak X}_1, \ldots , {\mathfrak X}_k$
be the corresponding (under h) finitely many definably connected components of
![]() ${\mathfrak X}$
, and let
${\mathfrak X}$
, and let
![]() ${\mathcal {U}}$
be the set of definably connected components of
${\mathcal {U}}$
be the set of definably connected components of
![]() $\widehat {X}$
.
$\widehat {X}$
.
Now if
![]() $U\in {\mathcal {U}}$
is a definably connected component of
$U\in {\mathcal {U}}$
is a definably connected component of
![]() $\widehat {X},$
there is
$\widehat {X},$
there is
![]() $i\in \{1, \ldots , k\}$
such that
$i\in \{1, \ldots , k\}$
such that
![]() $g(U)\subseteq {\mathcal X}_{i}$
. Indeed, if
$g(U)\subseteq {\mathcal X}_{i}$
. Indeed, if
![]() $i,i'$
are distinct such that
$i,i'$
are distinct such that
![]() $g(U)\cap {\mathcal X}_i\neq \emptyset $
and
$g(U)\cap {\mathcal X}_i\neq \emptyset $
and
![]() $g(U)\cap {\mathcal X}_{i'}\neq \emptyset ,$
then since
$g(U)\cap {\mathcal X}_{i'}\neq \emptyset ,$
then since
![]() $g^{-1}({\mathcal X}_i)$
and
$g^{-1}({\mathcal X}_i)$
and
![]() $g^{-1}({\mathcal X}_{i'})$
are relatively definable (Lemma 5.17) by Lemma 5.16 (a) and continuity of
$g^{-1}({\mathcal X}_{i'})$
are relatively definable (Lemma 5.17) by Lemma 5.16 (a) and continuity of
![]() $g,$
both
$g,$
both
![]() $g^{-1}({\mathcal X}_i)\cap U$
and
$g^{-1}({\mathcal X}_i)\cap U$
and
![]() $g^{-1}({\mathcal X}_{i'})\cap U$
would be clopen strict pro-definable subsets of U distinct from
$g^{-1}({\mathcal X}_{i'})\cap U$
would be clopen strict pro-definable subsets of U distinct from
![]() $\emptyset $
and U.
$\emptyset $
and U.
Fix i, and let
![]() ${\mathcal {U}} _i=\{U\in {\mathcal {U}}: f(U)\subseteq {\mathfrak X}_i\}$
. For each
${\mathcal {U}} _i=\{U\in {\mathcal {U}}: f(U)\subseteq {\mathfrak X}_i\}$
. For each
![]() $U\in {\mathcal {U}}_i$
, choose
$U\in {\mathcal {U}}_i$
, choose
![]() $x_U\in U$
and consider the definable path
$x_U\in U$
and consider the definable path
![]() $\gamma _U\colon I\to \widehat {X}$
given by
$\gamma _U\colon I\to \widehat {X}$
given by
![]() $\gamma _U(t)=H(t, x_U)$
. Let
$\gamma _U(t)=H(t, x_U)$
. Let
![]() $x^{\prime }_U=\gamma (e_I)\in f(U)\subseteq {\mathfrak X}_{i}$
. Since cells in
$x^{\prime }_U=\gamma (e_I)\in f(U)\subseteq {\mathfrak X}_{i}$
. Since cells in
![]() ${\Gamma ^k}$
are definably path connected ([Reference van den Dries53, Chapter 6, Proposition 3.2]) and cells in
${\Gamma ^k}$
are definably path connected ([Reference van den Dries53, Chapter 6, Proposition 3.2]) and cells in
![]() ${\Gamma ^k_{\infty } }$
are definably homeomorphic to cells in
${\Gamma ^k_{\infty } }$
are definably homeomorphic to cells in
![]() ${\Gamma ^k},$
by cell decomposition, any definable subset of
${\Gamma ^k},$
by cell decomposition, any definable subset of
![]() ${\Gamma ^k_{\infty } }$
can be partitioned into finitely many definably path connected subsets. So
${\Gamma ^k_{\infty } }$
can be partitioned into finitely many definably path connected subsets. So
![]() ${\mathfrak X}_i$
can be partitioned into finitely many
${\mathfrak X}_i$
can be partitioned into finitely many
![]() ${\mathfrak X}_{i,1}\ldots , {\mathfrak X}_{i, l}$
definably path-connected subsets.
${\mathfrak X}_{i,1}\ldots , {\mathfrak X}_{i, l}$
definably path-connected subsets.
Let
![]() $j_U$
be such that
$j_U$
be such that
![]() $x^{\prime }_U\in {\mathfrak X}_{i, j_U}$
. We claim that the map
$x^{\prime }_U\in {\mathfrak X}_{i, j_U}$
. We claim that the map
![]() ${\mathcal {U}}_i\to \{1,\ldots , l\}\colon U\mapsto j_U$
is injective, so
${\mathcal {U}}_i\to \{1,\ldots , l\}\colon U\mapsto j_U$
is injective, so
![]() ${\mathcal {U}}_i$
is finite. Hence
${\mathcal {U}}_i$
is finite. Hence
![]() ${\mathcal {U}}$
is finite as well. Indeed, suppose that
${\mathcal {U}}$
is finite as well. Indeed, suppose that
![]() $U,V\in {\mathcal {U}}$
are distinct and
$U,V\in {\mathcal {U}}$
are distinct and
![]() $j_U=j_V=j$
. Then
$j_U=j_V=j$
. Then
![]() $x^{\prime }_U, x^{\prime }_V\in {\mathfrak X}_{i, j}$
, so there is a definable path in
$x^{\prime }_U, x^{\prime }_V\in {\mathfrak X}_{i, j}$
, so there is a definable path in
![]() ${\mathfrak X}_{i,j}$
from
${\mathfrak X}_{i,j}$
from
![]() $x^{\prime }_U$
to
$x^{\prime }_U$
to
![]() $x^{\prime }_V$
. It follows that there is a definable path
$x^{\prime }_V$
. It follows that there is a definable path
![]() $\delta \colon J\to \widehat {X}$
from
$\delta \colon J\to \widehat {X}$
from
![]() $x_U\in U$
to
$x_U\in U$
to
![]() $x_V\in V$
. But by Lemma 5.19, both U and V are the stable completions of
$x_V\in V$
. But by Lemma 5.19, both U and V are the stable completions of
![]() $\mathrm {v\!+\!g}$
-clopen subsets of X, so they are relatively definable subsets of
$\mathrm {v\!+\!g}$
-clopen subsets of X, so they are relatively definable subsets of
![]() $\widehat {X}$
. It follows by Lemma 5.17 and continuity of
$\widehat {X}$
. It follows by Lemma 5.17 and continuity of
![]() $\delta $
that both
$\delta $
that both
![]() $\delta ^{-1}(U)$
and
$\delta ^{-1}(U)$
and
![]() $\delta ^{-1}(V)$
would be clopen (relatively) definable subsets of J distinct from
$\delta ^{-1}(V)$
would be clopen (relatively) definable subsets of J distinct from
![]() $\emptyset $
and
$\emptyset $
and
![]() $J,$
contradicting the definable connectedness of J.
$J,$
contradicting the definable connectedness of J.
If V is not quasi-projective, consider an open immersion
![]() $V\rightarrow W$
, where W is a complete variety and V is Zariski dense. By Chow’s lemma, there is an epimorphism
$V\rightarrow W$
, where W is a complete variety and V is Zariski dense. By Chow’s lemma, there is an epimorphism
![]() $f\colon W'\to W$
, where
$f\colon W'\to W$
, where
![]() $W'$
is a projective variety. Consider the quasi-projective variety
$W'$
is a projective variety. Consider the quasi-projective variety
![]() $V'=f^{-1}(V)$
. Now if
$V'=f^{-1}(V)$
. Now if
![]() $X'=(f,\mathrm {id})^{-1}(X) \subseteq V'\times {\Gamma ^n_{\infty } }, \ \widehat {X'}$
has finitely many definably connected components. Since
$X'=(f,\mathrm {id})^{-1}(X) \subseteq V'\times {\Gamma ^n_{\infty } }, \ \widehat {X'}$
has finitely many definably connected components. Since
![]() $(f,\mathrm {id})$
pulls back
$(f,\mathrm {id})$
pulls back
![]() $\mathrm {v\!+\!g}$
-clopen subsets to
$\mathrm {v\!+\!g}$
-clopen subsets to
![]() $\mathrm {v\!+\!g}$
-clopen subsets, by Lemma 5.19, we see that
$\mathrm {v\!+\!g}$
-clopen subsets, by Lemma 5.19, we see that
![]() $\widehat {X}$
has finitely many definably connected components.
$\widehat {X}$
has finitely many definably connected components.
Proposition 5.22. Let V be an algebraic variety, and let
![]() $X \subseteq V\times {\Gamma ^n_{\infty } }$
be a definable set. Then the
$X \subseteq V\times {\Gamma ^n_{\infty } }$
be a definable set. Then the
![]() $\widehat {\mathrm {v\!+\!g}}$
-site
$\widehat {\mathrm {v\!+\!g}}$
-site
![]() $\widehat {X}_{\widehat {\mathrm {v\!+\!g}}}$
is a
$\widehat {X}_{\widehat {\mathrm {v\!+\!g}}}$
is a
![]() ${\mathcal {T}}$
-space.
${\mathcal {T}}$
-space.
Proof. As we already saw, the
![]() $\widehat {\mathrm {v\!+\!g}}$
-open sets of
$\widehat {\mathrm {v\!+\!g}}$
-open sets of
![]() $\widehat {X}$
form a basis for the topology and are closed under finite unions and intersections, which shows conditions (i) and (ii) in Definition 3.2. Since clopen
$\widehat {X}$
form a basis for the topology and are closed under finite unions and intersections, which shows conditions (i) and (ii) in Definition 3.2. Since clopen
![]() $\widehat {\mathrm {v\!+\!g}}$
-subsets are exactly the
$\widehat {\mathrm {v\!+\!g}}$
-subsets are exactly the
![]() $\widehat {\mathrm {v\!+\!g}}$
-clopen subsets, condition (iii) follows from Lemmas 5.19 and 5.21
$\widehat {\mathrm {v\!+\!g}}$
-clopen subsets, condition (iii) follows from Lemmas 5.19 and 5.21
Note that the previous argument does not hold for
![]() $X_{\mathrm {v\!+\!g}}$
because there are more clopen
$X_{\mathrm {v\!+\!g}}$
because there are more clopen
![]() $\mathrm {v\!+\!g}$
-subsets than
$\mathrm {v\!+\!g}$
-subsets than
![]() $\mathrm {v\!+\!g}$
-clopen subsets (for example, the maximal ideal is a clopen
$\mathrm {v\!+\!g}$
-clopen subsets (for example, the maximal ideal is a clopen
![]() $\mathrm {v\!+\!g}$
-subset but not a
$\mathrm {v\!+\!g}$
-subset but not a
![]() $\mathrm {v\!+\!g}$
-clopen).
$\mathrm {v\!+\!g}$
-clopen).
5.4 Definable compactness and
 $\widehat {\mathrm {v\!+\!g}}$
-normality
$\widehat {\mathrm {v\!+\!g}}$
-normality
In this subsection, we recall the notion of definable compactness in stable completion, we show that the notion of weakly
![]() $\mathrm {v\!+\!g}$
-normality (Definition 3.14) corresponds to
$\mathrm {v\!+\!g}$
-normality (Definition 3.14) corresponds to
![]() $\widehat {\mathrm {v\!+\!g}}$
-normality (Definition 3.11), and we prove that every
$\widehat {\mathrm {v\!+\!g}}$
-normality (Definition 3.11), and we prove that every
![]() $\mathrm {v\!+\!g}$
-locally closed subset of
$\mathrm {v\!+\!g}$
-locally closed subset of
![]() $V\times {\Gamma ^n_{\infty } }$
is the union of finitely many
$V\times {\Gamma ^n_{\infty } }$
is the union of finitely many
![]() $\mathrm {v\!+\!g}$
-open subsets that are weakly
$\mathrm {v\!+\!g}$
-open subsets that are weakly
![]() $\mathrm {v\!+\!g}$
-normal.
$\mathrm {v\!+\!g}$
-normal.
Since the notion of a definable type on a definable set can be extended naturally to pro-definable sets, definable compactness of pro-definable topological spaces is defined by replacing curves by definable types; see [Reference Hrushovski and Loeser35, Section 4.1]. Also recall that if V is an algebraic variety over a valued field, then we say that a subset W of V is bounded if there exists an affine cover
![]() $V=\bigcup _{i=1}^mU_i,$
and subsets
$V=\bigcup _{i=1}^mU_i,$
and subsets
![]() $W_i\subseteq U_i$
such that
$W_i\subseteq U_i$
such that
![]() $W=\bigcup _{i=1}^mW_i$
and each
$W=\bigcup _{i=1}^mW_i$
and each
![]() $W_i$
is contained in a closed m-ball with radius in
$W_i$
is contained in a closed m-ball with radius in
![]() ${\Gamma };$
we say that a subset of
${\Gamma };$
we say that a subset of
![]() ${\Gamma ^m_{\infty } }$
is bounded if it is contained in
${\Gamma ^m_{\infty } }$
is bounded if it is contained in
![]() $[a, \infty ]^m$
for some a. More generally, we say that a subset W of
$[a, \infty ]^m$
for some a. More generally, we say that a subset W of
![]() $V\times {\Gamma ^m_{\infty } }$
is bounded if its pullback under
$V\times {\Gamma ^m_{\infty } }$
is bounded if its pullback under
![]() $\mathrm {id}\times \mathrm {val} \colon V\times \mathbb {A} ^m\to V\times {\Gamma ^m_{\infty } }$
is bounded.
$\mathrm {id}\times \mathrm {val} \colon V\times \mathbb {A} ^m\to V\times {\Gamma ^m_{\infty } }$
is bounded.
A pro-definable topological space Z is definably compact if and only if every definable type p on Z has a limit in Z: that is, there is a point
![]() $a\in Z$
such that for every open definable subset U of
$a\in Z$
such that for every open definable subset U of
![]() $Z,$
the definable type p concentrates on U.
$Z,$
the definable type p concentrates on U.
Remark 5.23 (Definable compactness in the stable completion).
By [Reference Hrushovski and Loeser35, Corollary 4.2.22], if V is an algebraic variety over a valued field F and X is a definable subset of
![]() $V\times {\Gamma ^m_{\infty } },$
then:
$V\times {\Gamma ^m_{\infty } },$
then:
-
•
 $\widehat {X}$
is definably compact if and only if X is bounded and
$\widehat {X}$
is definably compact if and only if X is bounded and
 $\mathrm {v\!+\!g}$
-closed.
$\mathrm {v\!+\!g}$
-closed.
Furthermore ([Reference Hrushovski and Loeser35, Proposition 4.2.30]), an algebraic variety over a valued field is complete if and only if its stable completion is definably compact.
The following is a special case of [Reference Hrushovski and Loeser35, Lemma 4.2.23]:
Remark 5.24. Let
![]() $V, V'$
be varieties,
$V, V'$
be varieties,
![]() $X\subseteq V\times {\Gamma ^m_{\infty } }$
and
$X\subseteq V\times {\Gamma ^m_{\infty } }$
and
![]() $Y\subseteq V'\times {\Gamma ^n_{\infty } }$
be definable subsets and
$Y\subseteq V'\times {\Gamma ^n_{\infty } }$
be definable subsets and
![]() $f\colon X\to Y$
be a definable map that is a morphism of
$f\colon X\to Y$
be a definable map that is a morphism of
![]() $\mathrm {v\!+\!g}$
-sites. If X is bounded and
$\mathrm {v\!+\!g}$
-sites. If X is bounded and
![]() $\mathrm {v\!+\!g}$
-closed, then f is
$\mathrm {v\!+\!g}$
-closed, then f is
![]() $\mathrm {v\!+\!g}$
-closed: that is, f maps
$\mathrm {v\!+\!g}$
-closed: that is, f maps
![]() $\mathrm {v\!+\!g}$
-closed subsets of X to
$\mathrm {v\!+\!g}$
-closed subsets of X to
![]() $\mathrm {v\!+\!g}$
-closed subsets of Y.
$\mathrm {v\!+\!g}$
-closed subsets of Y.
Indeed, if
![]() $Z\subseteq X$
is a
$Z\subseteq X$
is a
![]() $\mathrm {v\!+\!g}$
-closed subset, then
$\mathrm {v\!+\!g}$
-closed subset, then
![]() $\widehat {Z}\subseteq \widehat {X}$
is a closed relatively definable subset and
$\widehat {Z}\subseteq \widehat {X}$
is a closed relatively definable subset and
![]() $\widehat {f}(\widehat {Z})\subseteq \widehat {Y}$
is a closed subset ([Reference Hrushovski and Loeser35, Lemma 4.2.23]). On the other hand, applying [Reference Hrushovski and Loeser35, Lemma 4.2.6] to the surjective definable map
$\widehat {f}(\widehat {Z})\subseteq \widehat {Y}$
is a closed subset ([Reference Hrushovski and Loeser35, Lemma 4.2.23]). On the other hand, applying [Reference Hrushovski and Loeser35, Lemma 4.2.6] to the surjective definable map
![]() $f\colon X\to f(X),$
we get that the map
$f\colon X\to f(X),$
we get that the map
![]() $\widehat {f}\colon \widehat {X}\to \widehat {f(X)}$
is also surjective, which implies that
$\widehat {f}\colon \widehat {X}\to \widehat {f(X)}$
is also surjective, which implies that
![]() $\widehat {f(Z)}=\widehat {f}(\widehat {Z})$
, so
$\widehat {f(Z)}=\widehat {f}(\widehat {Z})$
, so
![]() $f(Z)$
is
$f(Z)$
is
![]() $\mathrm {v\!+\!g}$
-closed (Fact 5.11).
$\mathrm {v\!+\!g}$
-closed (Fact 5.11).
Recall the notion of weakly
![]() ${\mathcal {T}}$
-normal from Definition 3.14. Then:
${\mathcal {T}}$
-normal from Definition 3.14. Then:
Remark 5.25. Since open (respectively, closed)
![]() $\widehat {\mathrm {v\!+\!g}}$
-subsets of
$\widehat {\mathrm {v\!+\!g}}$
-subsets of
![]() $\widehat {X}$
are exactly the
$\widehat {X}$
are exactly the
![]() $\widehat {\mathrm {v\!+\!g}}$
-open (respectively,
$\widehat {\mathrm {v\!+\!g}}$
-open (respectively,
![]() $\widehat {\mathrm {v\!+\!g}}$
-closed) subsets of
$\widehat {\mathrm {v\!+\!g}}$
-closed) subsets of
![]() $\widehat {X}$
, we have that X is weakly
$\widehat {X}$
, we have that X is weakly
![]() $\mathrm {v\!+\!g}$
-normal if and only if
$\mathrm {v\!+\!g}$
-normal if and only if
![]() $\widehat {X}$
is
$\widehat {X}$
is
![]() $\widehat {\mathrm {v\!+\!g}}$
-normal (as in Definition 3.11).
$\widehat {\mathrm {v\!+\!g}}$
-normal (as in Definition 3.11).
For the next result, we need to recall the schematic distance function from [Reference Hrushovski and Loeser35, Section 3.12]. First, given
![]() $g(x_0,\ldots ,x_m)$
a homogeneous polynomial with coefficients in the valuation ring
$g(x_0,\ldots ,x_m)$
a homogeneous polynomial with coefficients in the valuation ring
![]() ${\mathcal {R}}$
, we define the function
${\mathcal {R}}$
, we define the function
![]() $\mathrm {val}(g)\colon \mathbb {P}^m\to [0,\infty ]$
by
$\mathrm {val}(g)\colon \mathbb {P}^m\to [0,\infty ]$
by
for some (any) i such that
![]() $\mathrm {val}(x_i)=\min \{\mathrm {val}(x_j): j=0,\ldots , m\}$
.
$\mathrm {val}(x_i)=\min \{\mathrm {val}(x_j): j=0,\ldots , m\}$
.
Let V be a projective variety and Z be a closed subvariety. Fix some embedding
![]() $\iota \colon V\to \mathbb {P}^m$
, and let
$\iota \colon V\to \mathbb {P}^m$
, and let
![]() $f=(f_1,\ldots , f_r)$
be a tuple of homogeneous polynomials in
$f=(f_1,\ldots , f_r)$
be a tuple of homogeneous polynomials in
![]() ${\mathcal {R}}[X_0,\ldots , X_m]$
such that Z is defined by the zero locus of f in V (note that by rescaling, one can always assume that the polynomials have coefficients in
${\mathcal {R}}[X_0,\ldots , X_m]$
such that Z is defined by the zero locus of f in V (note that by rescaling, one can always assume that the polynomials have coefficients in
![]() ${\mathcal {R}}$
). The schematic distance function to Z5 is the function
${\mathcal {R}}$
). The schematic distance function to Z5 is the function
![]() $\varphi _{\iota ,f}\colon V\to [0,\infty ]$
defined by
$\varphi _{\iota ,f}\colon V\to [0,\infty ]$
defined by
Note that
![]() $\varphi _{\iota ,f}$
is a morphism of
$\varphi _{\iota ,f}$
is a morphism of
![]() $\mathrm {v\!+\!g}$
-sites and
$\mathrm {v\!+\!g}$
-sites and
![]() $\varphi _{\iota ,f}^{-1}(\infty )=Z$
. In addition, if K is an elementary substructure of
$\varphi _{\iota ,f}^{-1}(\infty )=Z$
. In addition, if K is an elementary substructure of
![]() $\mathbb {U}$
and everything is defined over K, then the function
$\mathbb {U}$
and everything is defined over K, then the function
![]() $\varphi _{\iota ,f}$
is also K-definable.
$\varphi _{\iota ,f}$
is also K-definable.
Theorem 5.26. Let V be a variety, and let U be a basic
![]() $\mathrm {v\!+\!g}$
-open subset of V. Then U is weakly
$\mathrm {v\!+\!g}$
-open subset of V. Then U is weakly
![]() $\mathrm {v\!+\!g}$
-normal.
$\mathrm {v\!+\!g}$
-normal.
Proof. First we consider the case where V is a quasi-projective variety; then using Chow’s lemma, we treat the case V is a complete variety, and the general case will follow by Nagata’s theorem.
So suppose that V is a quasi-projective variety. Let
![]() $V'$
be a projective variety such that V is an open subset of
$V'$
be a projective variety such that V is an open subset of
![]() $V'$
. By fixing an embedding of
$V'$
. By fixing an embedding of
![]() $\iota \colon V'\to \mathbb {P}^m,$
we may suppose without loss of generality that
$\iota \colon V'\to \mathbb {P}^m,$
we may suppose without loss of generality that
![]() $V'\subseteq \mathbb {P}^m$
. Denote by Z the closed subvariety of
$V'\subseteq \mathbb {P}^m$
. Denote by Z the closed subvariety of
![]() $V'$
such that
$V'$
such that
![]() $V=V'\setminus Z,$
, and let
$V=V'\setminus Z,$
, and let
![]() $f=(f_1,\ldots , f_r)$
denote a finite tuple of homogeneous polynomials in
$f=(f_1,\ldots , f_r)$
denote a finite tuple of homogeneous polynomials in
![]() ${\mathcal {R}}[X_0, \ldots , X_m]$
defining Z in
${\mathcal {R}}[X_0, \ldots , X_m]$
defining Z in
![]() $V'$
.
$V'$
.
By Definition 5.2 and Fact 5.4, let L be a finite index set such that U is defined by
where
![]() $g_l, h_l$
are homogeneous polynomials on
$g_l, h_l$
are homogeneous polynomials on
![]() $V'$
of the same degree for each
$V'$
of the same degree for each
![]() $l\in L$
. By multiplying by a suitable constant, we may suppose for every
$l\in L$
. By multiplying by a suitable constant, we may suppose for every
![]() $l\in L$
that
$l\in L$
that
![]() $g_l, h_l$
have coefficients in
$g_l, h_l$
have coefficients in
![]() ${\mathcal {R}}$
and their composition under the valuation take values on
${\mathcal {R}}$
and their composition under the valuation take values on
![]() $[0,\infty ]$
.
$[0,\infty ]$
.
Let
![]() $C', D'$
be disjoint
$C', D'$
be disjoint
![]() $\mathrm {v\!+\!g}$
-closed subsets of U and
$\mathrm {v\!+\!g}$
-closed subsets of U and
![]() $C,D$
be
$C,D$
be
![]() $\mathrm {v\!+\!g}$
-closed subsets of
$\mathrm {v\!+\!g}$
-closed subsets of
![]() $V'$
such that
$V'$
such that
![]() $C\cap U=C'$
and
$C\cap U=C'$
and
![]() $D\cap U=D'$
. Again, by Fact 5.4, we may suppose that for some finite index sets I and J, we have
$D\cap U=D'$
. Again, by Fact 5.4, we may suppose that for some finite index sets I and J, we have
 $$\begin{align*}C=\bigcup _{i\in I}\bigcap _{j\in J}\{x\in V':p_{ij}(x)=0,\,\,\mathrm{val}(q_{ij}(x))\leq \mathrm{val}(r_{ij}(x))\}, \end{align*}$$
$$\begin{align*}C=\bigcup _{i\in I}\bigcap _{j\in J}\{x\in V':p_{ij}(x)=0,\,\,\mathrm{val}(q_{ij}(x))\leq \mathrm{val}(r_{ij}(x))\}, \end{align*}$$
where
![]() $p_{ij}, q_{ij}$
and
$p_{ij}, q_{ij}$
and
![]() $r_{ij}$
are homogeneous polynomials on
$r_{ij}$
are homogeneous polynomials on
![]() $V'$
with
$V'$
with
![]() $q_{ij}$
s and
$q_{ij}$
s and
![]() $r_{ij}$
s of the same degree. As before, we may assume that all such polynomials have coefficients in
$r_{ij}$
s of the same degree. As before, we may assume that all such polynomials have coefficients in
![]() ${\mathcal {R}}$
and their compositions under the valuation take values on
${\mathcal {R}}$
and their compositions under the valuation take values on
![]() $[0,\infty ]$
.
$[0,\infty ]$
.
Let
![]() $k =1+2|L|+3|I\times J|$
, and consider the definable map
$k =1+2|L|+3|I\times J|$
, and consider the definable map
![]() $d\colon V'\to [0,\infty ]^k$
given by
$d\colon V'\to [0,\infty ]^k$
given by
where
![]() $\varphi _{\iota , f}\colon V'\to [0,\infty ]$
is the schematic distance to Z as defined above. (Recall that
$\varphi _{\iota , f}\colon V'\to [0,\infty ]$
is the schematic distance to Z as defined above. (Recall that
![]() $\varphi _{\iota ,f}(x)=\infty $
if and only if
$\varphi _{\iota ,f}(x)=\infty $
if and only if
![]() $x \in Z$
.)
$x \in Z$
.)
The function d is a morphism of
![]() $\mathrm {v\!+\!g}$
-sites, as every coordinate function has this property. It is also
$\mathrm {v\!+\!g}$
-sites, as every coordinate function has this property. It is also
![]() $\mathrm {v\!+\!g}$
-closed by Remarks 5.23 and 5.24.
$\mathrm {v\!+\!g}$
-closed by Remarks 5.23 and 5.24.
Consider the set
and let
![]() $Y:= [0,\infty )\times A\times [0,\infty ]^{3|I\times J|}$
. Note that by the choice of d, we have
$Y:= [0,\infty )\times A\times [0,\infty ]^{3|I\times J|}$
. Note that by the choice of d, we have
![]() $d(U)\subseteq Y$
.
$d(U)\subseteq Y$
.
Claim 5.27. The sets
![]() $d(C')$
and
$d(C')$
and
![]() $d(D')$
are closed in Y and, in addition,
$d(D')$
are closed in Y and, in addition,
![]() $d(C')\cap d(D')=\emptyset $
.
$d(C')\cap d(D')=\emptyset $
.
Proof. Since d is a
![]() $\mathrm {v\!+\!g}$
-closed morphism of
$\mathrm {v\!+\!g}$
-closed morphism of
![]() $\mathrm {v\!+\!g}$
-sites,
$\mathrm {v\!+\!g}$
-sites,
![]() $d(C)$
and
$d(C)$
and
![]() $d(D)$
are closed. Moreover, by the choice of d,
$d(D)$
are closed. Moreover, by the choice of d,
This show
![]() $d(C')$
and
$d(C')$
and
![]() $d(D')$
are closed in Y. For the second part, suppose there were
$d(D')$
are closed in Y. For the second part, suppose there were
![]() $x\in C'$
and
$x\in C'$
and
![]() $y\in D'$
such that
$y\in D'$
such that
![]() $d(x)=d(y)$
. This implies
$d(x)=d(y)$
. This implies
![]() $y\in C'$
, contradicting that
$y\in C'$
, contradicting that
![]() $C'\cap D'=\emptyset $
. This completes the claim.
$C'\cap D'=\emptyset $
. This completes the claim.
To conclude the case V is quasi-projective, it suffices to show that Y is definably normal. Indeed, the definable normality of Y and Claim 5.27 imply there are disjoint open definable sets
![]() $U_1, U_2$
of Y such that
$U_1, U_2$
of Y such that
![]() $d(C')\subseteq U_1$
and
$d(C')\subseteq U_1$
and
![]() $d(D')\subseteq U_2$
. We obtain that
$d(D')\subseteq U_2$
. We obtain that
![]() $C'\subseteq d^{-1}(U_1)$
,
$C'\subseteq d^{-1}(U_1)$
,
![]() $D'\subseteq d^{-1}(U_2)$
and
$D'\subseteq d^{-1}(U_2)$
and
![]() $d^{-1}(U_1)\cap d^{-1}(U_2)=\emptyset $
. In addition, both
$d^{-1}(U_1)\cap d^{-1}(U_2)=\emptyset $
. In addition, both
![]() $d^{-1}(U_1)$
and
$d^{-1}(U_1)$
and
![]() $d^{-1}(U_2)$
are
$d^{-1}(U_2)$
are
![]() $\mathrm {v\!+\!g}$
-open since d is a morphism of
$\mathrm {v\!+\!g}$
-open since d is a morphism of
![]() $\mathrm {v\!+\!g}$
-sites, which shows U is weakly
$\mathrm {v\!+\!g}$
-sites, which shows U is weakly
![]() $\mathrm {v\!+\!g}$
-normal.
$\mathrm {v\!+\!g}$
-normal.
To show the definable normality of
![]() $Y,$
first note that the definable map
$Y,$
first note that the definable map
![]() $h\colon A\to A'$
given by
$h\colon A\to A'$
given by
![]() $h((\alpha _l,\gamma _l)_{l\in L})=(\alpha _l, \gamma _l-\alpha _l)_{l\in L},$
, where
$h((\alpha _l,\gamma _l)_{l\in L})=(\alpha _l, \gamma _l-\alpha _l)_{l\in L},$
, where
![]() $A':= ([0,\infty )\times [0,\infty ])^{|L|}$
, is a definable homeomorphism. Therefore, Y is definably normal if and only if the set
$A':= ([0,\infty )\times [0,\infty ])^{|L|}$
, is a definable homeomorphism. Therefore, Y is definably normal if and only if the set
is definably normal, and
![]() $Y'$
is definably normal by [Reference Edmundo and Prelli28, Theorem 2.20]).
$Y'$
is definably normal by [Reference Edmundo and Prelli28, Theorem 2.20]).
Now suppose that V is a complete variety. By Chow’s lemma, there are a projective variety
![]() $V'$
and a surjective morphism
$V'$
and a surjective morphism
![]() $g\colon V'\to V$
. Consider the quasi-projective variety
$g\colon V'\to V$
. Consider the quasi-projective variety
![]() $Y:= g^{-1}(V)$
and the basic
$Y:= g^{-1}(V)$
and the basic
![]() $\mathrm {v\!+\!g}$
-open subset
$\mathrm {v\!+\!g}$
-open subset
![]() $W:= g^{-1}(U)$
of Y.
$W:= g^{-1}(U)$
of Y.
Let
![]() $U_1'$
and
$U_1'$
and
![]() $U_2'$
be
$U_2'$
be
![]() $\mathrm {v\!+\!g}$
-open subsets of U such that
$\mathrm {v\!+\!g}$
-open subsets of U such that
![]() $U_1'\cup U_2'=U$
. By (3) of Definition 3.14, it suffices to find
$U_1'\cup U_2'=U$
. By (3) of Definition 3.14, it suffices to find
![]() $D_1\subseteq U_1'$
and
$D_1\subseteq U_1'$
and
![]() $D_2\subseteq U_2' \ \mathrm {v\!+\!g}$
-closed subsets of U such that
$D_2\subseteq U_2' \ \mathrm {v\!+\!g}$
-closed subsets of U such that
![]() $D_1\cup D_2=U$
. By definition of being
$D_1\cup D_2=U$
. By definition of being
![]() $\mathrm {v\!+\!g}$
-open in
$\mathrm {v\!+\!g}$
-open in
![]() $U,$
there are
$U,$
there are
![]() $U_1$
and
$U_1$
and
![]() $U_2 \ \mathrm {v\!+\!g}$
-open subsets of V such that
$U_2 \ \mathrm {v\!+\!g}$
-open subsets of V such that
![]() $U_1'=U_1\cap U$
and
$U_1'=U_1\cap U$
and
![]() $U_2'=U_2\cap U$
. Since g is a morphism of
$U_2'=U_2\cap U$
. Since g is a morphism of
![]() $\mathrm {v\!+\!g}$
-sites,
$\mathrm {v\!+\!g}$
-sites,
![]() $g^{-1}(U_1)$
and
$g^{-1}(U_1)$
and
![]() $g^{-1}(U_2)$
are
$g^{-1}(U_2)$
are
![]() $\mathrm {v\!+\!g}$
-open. For
$\mathrm {v\!+\!g}$
-open. For
![]() $i=1,2$
, set
$i=1,2$
, set
![]() $W_i=g^{-1}(U_i')$
. Note that
$W_i=g^{-1}(U_i')$
. Note that
![]() $W_i=g^{-1}(U_i)\cap W$
for
$W_i=g^{-1}(U_i)\cap W$
for
![]() $i=1,2$
. In particular,
$i=1,2$
. In particular,
![]() $W_1\cup W_2=W$
and
$W_1\cup W_2=W$
and
![]() $W_i$
is
$W_i$
is
![]() $\mathrm {v\!+\!g}$
-open in W for
$\mathrm {v\!+\!g}$
-open in W for
![]() $i=1,2$
. By the quasi-projective case and (3) of Definition 3.14, there are
$i=1,2$
. By the quasi-projective case and (3) of Definition 3.14, there are
![]() $\mathrm {v\!+\!g}$
-closed subsets
$\mathrm {v\!+\!g}$
-closed subsets
![]() $C_1'\subseteq W_1$
and
$C_1'\subseteq W_1$
and
![]() $C_2'\subseteq W_2$
of W such that
$C_2'\subseteq W_2$
of W such that
![]() $C_1'\cup C_2'=W$
. By definition, this implies there are
$C_1'\cup C_2'=W$
. By definition, this implies there are
![]() $\mathrm {v\!+\!g}$
-closed subsets
$\mathrm {v\!+\!g}$
-closed subsets
![]() $C_i\subseteq Y$
such that
$C_i\subseteq Y$
such that
![]() $C_i'=C_i\cap W$
.
$C_i'=C_i\cap W$
.
By Remark 5.24, the map g is
![]() $\mathrm {v\!+\!g}$
-closed. Then
$\mathrm {v\!+\!g}$
-closed. Then
![]() $g(C_1), g(C_2)$
are
$g(C_1), g(C_2)$
are
![]() $\mathrm {v\!+\!g}$
-closed subsets of V. We let the reader check that the sets
$\mathrm {v\!+\!g}$
-closed subsets of V. We let the reader check that the sets
![]() $D_i:= g(C_i)\cap U$
defined for
$D_i:= g(C_i)\cap U$
defined for
![]() $i=1,2$
are
$i=1,2$
are
![]() $\mathrm {v\!+\!g}$
-closed subsets of U that satisfy in addition that
$\mathrm {v\!+\!g}$
-closed subsets of U that satisfy in addition that
![]() $D_i\subseteq U_i'$
and
$D_i\subseteq U_i'$
and
![]() $D_1\cup D_2=U$
.
$D_1\cup D_2=U$
.
For the general case, by Nagata’s theorem, there is an open immersion
![]() $f\colon V\to V'$
, where
$f\colon V\to V'$
, where
![]() $V'$
is a complete variety. Therefore, V is homeomorphic to the open subset
$V'$
is a complete variety. Therefore, V is homeomorphic to the open subset
![]() $f(V)$
of
$f(V)$
of
![]() $V'$
and
$V'$
and
![]() $f\colon V\to f(V)$
is an isomorphism of
$f\colon V\to f(V)$
is an isomorphism of
![]() $\mathrm {v\!+\!g}$
-sites. In particular, since
$\mathrm {v\!+\!g}$
-sites. In particular, since
![]() $f(U)$
is a basic
$f(U)$
is a basic
![]() $\mathrm {v\!+\!g}$
-open subset of
$\mathrm {v\!+\!g}$
-open subset of
![]() $V'$
that, by the case for complete varieties, is weakly
$V'$
that, by the case for complete varieties, is weakly
![]() $\mathrm {v\!+\!g}$
-normal, the result follows.
$\mathrm {v\!+\!g}$
-normal, the result follows.
We now need to extend Theorem 5.26 to basic
![]() $\mathrm {v\!+\!g}$
-open subset of
$\mathrm {v\!+\!g}$
-open subset of
![]() $V\times {\Gamma ^n_{\infty } }$
. In order to do that, we require a couple of preliminaries.
$V\times {\Gamma ^n_{\infty } }$
. In order to do that, we require a couple of preliminaries.
Recall that if
![]() $\mathbb {V}$
is an elementary extension of
$\mathbb {V}$
is an elementary extension of
![]() $\mathbb {U}$
and
$\mathbb {U}$
and
![]() $p\in S_z(B)$
is a type over a subset B of
$p\in S_z(B)$
is a type over a subset B of
![]() $\mathbb {U},$
then p is realised in
$\mathbb {U},$
then p is realised in
![]() $\mathbb {V}$
if and only if there is
$\mathbb {V}$
if and only if there is
![]() $a\in \mathbb {V}^{|z|}$
such that
$a\in \mathbb {V}^{|z|}$
such that
![]() $p=\mathrm {tp}(a/B)$
where
$p=\mathrm {tp}(a/B)$
where
is the type of a over B. One says in this case that a is a realisation of p. Also recall that any type
![]() $p\in S_z(B)$
is realised in some elementary extension of
$p\in S_z(B)$
is realised in some elementary extension of
![]() $\mathbb {U}$
.
$\mathbb {U}$
.
Given definable global types
![]() $p\in S_x(\mathbb {U})$
and
$p\in S_x(\mathbb {U})$
and
![]() $q\in S_y(\mathbb {U}),$
the tensor product
$q\in S_y(\mathbb {U}),$
the tensor product
![]() $p\otimes q$
is the definable global type
$p\otimes q$
is the definable global type
![]() $\mathrm {tp}(a,b/\mathbb {U})$
, where a realises p and b realises
$\mathrm {tp}(a,b/\mathbb {U})$
, where a realises p and b realises
![]() $q|\mathbb {U}\cup \{a\}$
. Recall that for any
$q|\mathbb {U}\cup \{a\}$
. Recall that for any
![]() $B\supseteq \mathbb {U}$
, one denotes by
$B\supseteq \mathbb {U}$
, one denotes by
![]() $q|B$
the canonical extension of q to
$q|B$
the canonical extension of q to
![]() $S_y(B)$
given by
$S_y(B)$
given by
![]() $\phi (y,b)\in q|B$
if and only if
$\phi (y,b)\in q|B$
if and only if
![]() $d_q(\phi )(b)$
holds in some elementary extension
$d_q(\phi )(b)$
holds in some elementary extension
![]() $\mathbb {V}$
of
$\mathbb {V}$
of
![]() $\mathbb {U}$
containing B.
$\mathbb {U}$
containing B.
Note that
![]() $p\otimes q$
is indeed a definable global type with
$p\otimes q$
is indeed a definable global type with
![]() $d_{p\otimes q}(\theta )$
given by
$d_{p\otimes q}(\theta )$
given by
![]() $d_p(d_q(\theta ))$
. On the other hand, by [Reference Hrushovski and Loeser35, Proposition 2.9.1] and [Reference Hrushovski and Pillay36, Proposition 3.2], if the definable global types
$d_p(d_q(\theta ))$
. On the other hand, by [Reference Hrushovski and Loeser35, Proposition 2.9.1] and [Reference Hrushovski and Pillay36, Proposition 3.2], if the definable global types
![]() $p\in S_x(\mathbb {U})$
and
$p\in S_x(\mathbb {U})$
and
![]() $q\in S_y(\mathbb {U})$
are orthogonal to
$q\in S_y(\mathbb {U})$
are orthogonal to
![]() $\Gamma ,$
then
$\Gamma ,$
then
![]() $p\otimes q$
is orthogonal to
$p\otimes q$
is orthogonal to
![]() $\Gamma $
.
$\Gamma $
.
Lemma 5.28. Let
![]() $(\gamma _1,\ldots ,\gamma _n)\in \Gamma ^n$
and
$(\gamma _1,\ldots ,\gamma _n)\in \Gamma ^n$
and
![]() $b=(b_1,\ldots ,b_n)$
be a realisation of
$b=(b_1,\ldots ,b_n)$
be a realisation of
![]() $\eta _{\gamma _1}\otimes \cdots \otimes \eta _{\gamma _n}$
, where
$\eta _{\gamma _1}\otimes \cdots \otimes \eta _{\gamma _n}$
, where
![]() $\eta _{\gamma _i}:= \eta _{B(0,\gamma _i)}$
is as defined in Example 5.8. Then for every polynomial
$\eta _{\gamma _i}:= \eta _{B(0,\gamma _i)}$
is as defined in Example 5.8. Then for every polynomial
![]() $\sum a_jy^j\in \mathbb {U}[y]$
with
$\sum a_jy^j\in \mathbb {U}[y]$
with
![]() $y=(y_1,\ldots ,y_n)$
(in multi-index notation), it holds that
$y=(y_1,\ldots ,y_n)$
(in multi-index notation), it holds that
Proof. Let
![]() $c_i\in \mathbb {U}$
be such that
$c_i\in \mathbb {U}$
be such that
![]() $\mathrm {val}(c_i)=\gamma _i$
. In particular,
$\mathrm {val}(c_i)=\gamma _i$
. In particular,
![]() $\mathrm {val}(c_i^{-1}b_i)=0$
for all
$\mathrm {val}(c_i^{-1}b_i)=0$
for all
![]() $i\in \{1,\ldots ,n\}$
. The definition of the tensor product of definable global types yields that the set
$i\in \{1,\ldots ,n\}$
. The definition of the tensor product of definable global types yields that the set
is algebraically independent over the residue field k. It follows that every finite subset of distinct finite products of elements in A is k-linearly independent. Let
![]() $\sum _j e_j (c_1^{-1}b_1\cdots c_n^{-1}b_n)^j$
be a
$\sum _j e_j (c_1^{-1}b_1\cdots c_n^{-1}b_n)^j$
be a
![]() $\mathbb {U}$
-linear combination of distinct finite products of elements in
$\mathbb {U}$
-linear combination of distinct finite products of elements in
![]() $\{c_1^{-1}b_1,\cdots , c_n^{-1}b_n\}$
, where
$\{c_1^{-1}b_1,\cdots , c_n^{-1}b_n\}$
, where
![]() $e_j\in \mathbb {U}$
and we use the multi-index notation
$e_j\in \mathbb {U}$
and we use the multi-index notation
with
![]() $j=(j_1,\ldots ,j_n)\in \mathbb {N}^n$
. By [Reference Engler and Prestel30, Lemma 3.2.2], every such
$j=(j_1,\ldots ,j_n)\in \mathbb {N}^n$
. By [Reference Engler and Prestel30, Lemma 3.2.2], every such
![]() $\mathbb {U}$
-linear combination satisfies
$\mathbb {U}$
-linear combination satisfies
To conclude, given a polynomial
![]() $\sum a_jy^j$
in
$\sum a_jy^j$
in
![]() $\mathbb {U}[y]$
, consider the polynomial
$\mathbb {U}[y]$
, consider the polynomial
![]() $\sum _j a_j' y^j$
, where
$\sum _j a_j' y^j$
, where
![]() $a_j'= a_j(c_1^{j_1}\cdots c_n^{j_n})$
. By equation (4),
$a_j'= a_j(c_1^{j_1}\cdots c_n^{j_n})$
. By equation (4),
 $$ \begin{align*} \mathrm{val}(\sum a_jb^j) & =\mathrm{val}(\sum_j a_j'(c_1^{-1}b_1\cdots c_n^{-1}b_n)^j) = \min_j\{\mathrm{val}(a_j'(c_1^{-1}b_1\cdots c_n^{-1}b_n)^j)\}\\ & = \min_j\{\mathrm{val}(a_jb^j)\}.\\[-3.5pc] \end{align*} $$
$$ \begin{align*} \mathrm{val}(\sum a_jb^j) & =\mathrm{val}(\sum_j a_j'(c_1^{-1}b_1\cdots c_n^{-1}b_n)^j) = \min_j\{\mathrm{val}(a_j'(c_1^{-1}b_1\cdots c_n^{-1}b_n)^j)\}\\ & = \min_j\{\mathrm{val}(a_jb^j)\}.\\[-3.5pc] \end{align*} $$
A minor modification of [Reference Hrushovski and Loeser35, Lemma 3.5.2] shows the following:
Lemma 5.29. Let V be an algebraic variety. The map
 $$ \begin{align*} s\colon & \widehat{V}\times {\Gamma^n_{\infty} } \to \widehat{V\times \mathbb{A} ^n} \\ & (p, \gamma_1,\ldots,\gamma_n) \mapsto p\otimes \eta_{\gamma_1}\otimes \cdots\otimes \eta_{\gamma_n}, \end{align*} $$
$$ \begin{align*} s\colon & \widehat{V}\times {\Gamma^n_{\infty} } \to \widehat{V\times \mathbb{A} ^n} \\ & (p, \gamma_1,\ldots,\gamma_n) \mapsto p\otimes \eta_{\gamma_1}\otimes \cdots\otimes \eta_{\gamma_n}, \end{align*} $$
where
![]() $\eta _{\gamma _i}:= \eta _{B(0,\gamma _i)}$
is as in Example 5.8, is an injective morphism of
$\eta _{\gamma _i}:= \eta _{B(0,\gamma _i)}$
is as in Example 5.8, is an injective morphism of
![]() $\widehat {\mathrm {v\!+\!g}}$
-sites, which is a section of
$\widehat {\mathrm {v\!+\!g}}$
-sites, which is a section of
Proof. That s is a section of
![]() $\widehat {\mathrm {id}_V\times \mathrm {val}}$
and is injective is straightforward. Let us show it is a morphism of
$\widehat {\mathrm {id}_V\times \mathrm {val}}$
and is injective is straightforward. Let us show it is a morphism of
![]() $\widehat {\mathrm {v\!+\!g}}$
-sites. Since taking preimages preserves Boolean combinations, it is enough to consider the case
$\widehat {\mathrm {v\!+\!g}}$
-sites. Since taking preimages preserves Boolean combinations, it is enough to consider the case
![]() $V=\mathbb {A} ^m$
and show that if U is a
$V=\mathbb {A} ^m$
and show that if U is a
![]() $\mathrm {v\!+\!g}$
-open subset of
$\mathrm {v\!+\!g}$
-open subset of
![]() $\mathbb {A} ^{m+n}$
of the form
$\mathbb {A} ^{m+n}$
of the form
with
![]() $f_1,f_2\in \mathbb {U}[x,y]$
, then we have
$f_1,f_2\in \mathbb {U}[x,y]$
, then we have
![]() $s^{-1}(\widehat {U})=\widehat {W}$
for a
$s^{-1}(\widehat {U})=\widehat {W}$
for a
![]() $\mathrm {v\!+\!g}$
-open subset W of
$\mathrm {v\!+\!g}$
-open subset W of
![]() $\mathbb {A}^m\times {\Gamma ^n_{\infty } }$
.
$\mathbb {A}^m\times {\Gamma ^n_{\infty } }$
.
Suppose that
![]() $f_l(x,y)=\sum _j h_{l,j}(x)y^{j}$
with
$f_l(x,y)=\sum _j h_{l,j}(x)y^{j}$
with
![]() $y=(y_1, \ldots , y_n)$
(in multi-index notation). Let
$y=(y_1, \ldots , y_n)$
(in multi-index notation). Let
![]() $p\otimes \eta _{\gamma _1}\otimes \cdots \otimes \eta _{\gamma _n}\in s(\widehat {V}\times \Gamma _{\infty }^n)\cap \widehat {U}$
, and let
$p\otimes \eta _{\gamma _1}\otimes \cdots \otimes \eta _{\gamma _n}\in s(\widehat {V}\times \Gamma _{\infty }^n)\cap \widehat {U}$
, and let
![]() $(a,b)$
be a realisation of it,
$(a,b)$
be a realisation of it,
![]() $b=(b_1,\ldots , b_n)$
and
$b=(b_1,\ldots , b_n)$
and
![]() $\mathrm {val} (b_i)=\gamma _i$
. By Lemma 5.28 (applied to the field
$\mathrm {val} (b_i)=\gamma _i$
. By Lemma 5.28 (applied to the field
![]() $\mathbb {U}(a)$
), we have
$\mathbb {U}(a)$
), we have
 $$ \begin{align*} \mathrm{val}(f_l(a,b)) & =\min_{j} \mathrm{val}(h_{l,j}(a)b^{j})\\ & =P_l( (\mathrm{val} (h_{l,j}(a)))_j,\gamma_1,\ldots,\gamma_n), \end{align*} $$
$$ \begin{align*} \mathrm{val}(f_l(a,b)) & =\min_{j} \mathrm{val}(h_{l,j}(a)b^{j})\\ & =P_l( (\mathrm{val} (h_{l,j}(a)))_j,\gamma_1,\ldots,\gamma_n), \end{align*} $$
where the function
![]() $P_l\colon \Gamma _{\infty }^{d_l+m}\to \Gamma _{\infty }$
is obtained by composition of the natural continuous extensions of
$P_l\colon \Gamma _{\infty }^{d_l+m}\to \Gamma _{\infty }$
is obtained by composition of the natural continuous extensions of
![]() $\min $
and
$\min $
and
![]() $+$
. Here
$+$
. Here
![]() $d_l$
is the number of terms in the variable y in the polynomial
$d_l$
is the number of terms in the variable y in the polynomial
![]() $f_l$
.
$f_l$
.
It follows that, if
![]() $(p,\gamma )\in \widehat {V}\times {\Gamma ^n_{\infty } } $
with
$(p,\gamma )\in \widehat {V}\times {\Gamma ^n_{\infty } } $
with
![]() $\gamma =(\gamma _1, \ldots , \gamma _n),$
then we have
$\gamma =(\gamma _1, \ldots , \gamma _n),$
then we have
 $$ \begin{align*} (p,\gamma )\in s^{-1}(\widehat{U}) & \Leftrightarrow p\otimes \eta_{\gamma_1}\otimes \cdots\otimes \eta_{\gamma_n} \in \widehat{U}\\ & \Leftrightarrow \textrm{val} (f_1(a,b))<\textrm{val} (f_2(a,b))\,\,\,\textrm{for all}\,\,\, (a,b)\models p\otimes \eta_{\gamma_1}\otimes \cdots\otimes \eta_{\gamma_n} \\ & \Leftrightarrow P_1((\textrm{val} (h_{1,j}(a)))_j,\gamma)<P_2(\textrm{val} ((h_{2,j}(a)))_j,\gamma)\,\,\,\textrm{for all}\,\,\, a\models p. \end{align*} $$
$$ \begin{align*} (p,\gamma )\in s^{-1}(\widehat{U}) & \Leftrightarrow p\otimes \eta_{\gamma_1}\otimes \cdots\otimes \eta_{\gamma_n} \in \widehat{U}\\ & \Leftrightarrow \textrm{val} (f_1(a,b))<\textrm{val} (f_2(a,b))\,\,\,\textrm{for all}\,\,\, (a,b)\models p\otimes \eta_{\gamma_1}\otimes \cdots\otimes \eta_{\gamma_n} \\ & \Leftrightarrow P_1((\textrm{val} (h_{1,j}(a)))_j,\gamma)<P_2(\textrm{val} ((h_{2,j}(a)))_j,\gamma)\,\,\,\textrm{for all}\,\,\, a\models p. \end{align*} $$
Therefore, setting
W is a definable subset and
![]() $s^{-1}(\widehat {U})=\widehat {W}$
. On the other hand, since the pullback of W under
$s^{-1}(\widehat {U})=\widehat {W}$
. On the other hand, since the pullback of W under
![]() $\mathrm {id} \times \mathrm {val} $
is
$\mathrm {id} \times \mathrm {val} $
is
and
![]() $\min $
and
$\min $
and
![]() $+$
are continuous, it follows that
$+$
are continuous, it follows that
![]() $(\mathrm {id} \times \mathrm {val} )^{-1}(W)$
is
$(\mathrm {id} \times \mathrm {val} )^{-1}(W)$
is
![]() $\mathrm {v\!+\!g}$
-open subset, so, by definition, W is
$\mathrm {v\!+\!g}$
-open subset, so, by definition, W is
![]() $\mathrm {v\!+\!g}$
-open as required.
$\mathrm {v\!+\!g}$
-open as required.
Lemma 5.30. Let
![]() $f\colon (X,{\mathcal {T}}) \to (Y, {\mathcal {T}}')$
be a morphism in
$f\colon (X,{\mathcal {T}}) \to (Y, {\mathcal {T}}')$
be a morphism in
![]() ${\mathfrak T}$
with a section
${\mathfrak T}$
with a section
![]() $s\colon (Y,{\mathcal {T}}')\to (X,{\mathcal {T}})$
, which is also a morphism in
$s\colon (Y,{\mathcal {T}}')\to (X,{\mathcal {T}})$
, which is also a morphism in
![]() ${\mathfrak T}$
. If U is a
${\mathfrak T}$
. If U is a
![]() ${\mathcal {T}}$
-open subset of X, which is
${\mathcal {T}}$
-open subset of X, which is
![]() ${\mathcal {T}}$
-normal, then
${\mathcal {T}}$
-normal, then
![]() $s^{-1}(U)$
is a
$s^{-1}(U)$
is a
![]() ${\mathcal {T}}'$
-open subset of Y, which is
${\mathcal {T}}'$
-open subset of Y, which is
![]() ${\mathcal {T}}'$
-normal. In particular, if every
${\mathcal {T}}'$
-normal. In particular, if every
![]() ${\mathcal {T}}$
-open subset of X is a finite union of
${\mathcal {T}}$
-open subset of X is a finite union of
![]() ${\mathcal {T}}$
-open, which are
${\mathcal {T}}$
-open, which are
![]() ${\mathcal {T}}$
-normal subsets, then every
${\mathcal {T}}$
-normal subsets, then every
![]() ${\mathcal {T}}'$
-open subset of Y is a finite union of
${\mathcal {T}}'$
-open subset of Y is a finite union of
![]() ${\mathcal {T}}'$
-open, which are
${\mathcal {T}}'$
-open, which are
![]() ${\mathcal {T}}'$
-normal subsets.
${\mathcal {T}}'$
-normal subsets.
Proof. Let
![]() $C_1,C_2$
be two disjoint closed
$C_1,C_2$
be two disjoint closed
![]() ${\mathcal {T}}'$
-subsets of
${\mathcal {T}}'$
-subsets of
![]() $s^{-1}(U)$
. For
$s^{-1}(U)$
. For
![]() $i=1,2$
, let
$i=1,2$
, let
![]() $D_i:= f^{-1}(C_i)\cap U$
. Since f is a morphism in
$D_i:= f^{-1}(C_i)\cap U$
. Since f is a morphism in
![]() ${\mathfrak T},$
both
${\mathfrak T},$
both
![]() $D_1$
and
$D_1$
and
![]() $D_2$
are closed
$D_2$
are closed
![]() ${\mathcal {T}}$
-sets. Hence, there are disjoint open
${\mathcal {T}}$
-sets. Hence, there are disjoint open
![]() ${\mathcal {T}}$
-subsets
${\mathcal {T}}$
-subsets
![]() $U_1, U_2\subseteq U$
such that
$U_1, U_2\subseteq U$
such that
![]() $D_i\subseteq U_i$
for
$D_i\subseteq U_i$
for
![]() $i=1,2$
. Since s is a morphism in
$i=1,2$
. Since s is a morphism in
![]() ${\mathfrak T},$
the sets
${\mathfrak T},$
the sets
![]() $W_1:= s^{-1}(U_1)$
and
$W_1:= s^{-1}(U_1)$
and
![]() $W_2:= s^{-1}(U_1)$
are disjoint open
$W_2:= s^{-1}(U_1)$
are disjoint open
![]() ${\mathcal {T}}'$
-subsets of
${\mathcal {T}}'$
-subsets of
![]() $s^{-1}(U)$
and
$s^{-1}(U)$
and
![]() $C_i\subseteq W_i$
for
$C_i\subseteq W_i$
for
![]() $i=1,2$
since
$i=1,2$
since
![]() $f\circ s=\mathrm {id} $
.
$f\circ s=\mathrm {id} $
.
For the last part, just note that if
![]() $f^{-1}(W)=W^{\prime }_1\cup \ldots \cup W^{\prime }_l,$
then
$f^{-1}(W)=W^{\prime }_1\cup \ldots \cup W^{\prime }_l,$
then
![]() $W=s^{-1}(W^{\prime }_1)\cup \ldots \cup s^{-1}(W^{\prime }_l)$
.
$W=s^{-1}(W^{\prime }_1)\cup \ldots \cup s^{-1}(W^{\prime }_l)$
.
Corollary 5.31. Let V be a variety. Then every
![]() $\mathrm {v\!+\!g}$
-locally closed subset X of
$\mathrm {v\!+\!g}$
-locally closed subset X of
![]() $V\times {\Gamma ^n_{\infty } }$
is the union of finitely many basic
$V\times {\Gamma ^n_{\infty } }$
is the union of finitely many basic
![]() $\mathrm {v\!+\!g}$
-open subsets of X that are weakly
$\mathrm {v\!+\!g}$
-open subsets of X that are weakly
![]() $\mathrm {v\!+\!g}$
-normal. In fact, every basic
$\mathrm {v\!+\!g}$
-normal. In fact, every basic
![]() $\mathrm {v\!+\!g}$
-open subset of
$\mathrm {v\!+\!g}$
-open subset of
![]() $V\times {\Gamma ^n_{\infty } }$
is weakly
$V\times {\Gamma ^n_{\infty } }$
is weakly
![]() $\mathrm {v\!+\!g}$
-normal.
$\mathrm {v\!+\!g}$
-normal.
Proof. It suffices to show the result for
![]() $\mathrm {v\!+\!g}$
-open subset as every
$\mathrm {v\!+\!g}$
-open subset as every
![]() $\mathrm {v\!+\!g}$
-closed subset of a weakly
$\mathrm {v\!+\!g}$
-closed subset of a weakly
![]() $\mathrm {v\!+\!g}$
-normal set is again weakly
$\mathrm {v\!+\!g}$
-normal set is again weakly
![]() $\mathrm {v\!+\!g}$
-normal. By the isomorphism of sites
$\mathrm {v\!+\!g}$
-normal. By the isomorphism of sites
![]() $(V\times \mathbb {A}^n)_{\mathrm {v\!+\!g}}$
and
$(V\times \mathbb {A}^n)_{\mathrm {v\!+\!g}}$
and
![]() $(\widehat {V\times \mathbb {A} ^n})_{\mathrm {v\!+\!g}}$
and Theorem 5.26 and Remark 5.25, the result holds for
$(\widehat {V\times \mathbb {A} ^n})_{\mathrm {v\!+\!g}}$
and Theorem 5.26 and Remark 5.25, the result holds for
![]() $\widehat {\mathrm {v\!+\!g}}$
-open subsets of
$\widehat {\mathrm {v\!+\!g}}$
-open subsets of
![]() $\widehat {V\times \mathbb {A} ^n}$
. By Lemmas 5.29 and 5.30, the result holds for
$\widehat {V\times \mathbb {A} ^n}$
. By Lemmas 5.29 and 5.30, the result holds for
![]() $\widehat {\mathrm {v\!+\!g}}$
-open subsets of
$\widehat {\mathrm {v\!+\!g}}$
-open subsets of
![]() $\widehat {V\times {\Gamma ^n_{\infty } }}$
. So by the isomorphism of sites
$\widehat {V\times {\Gamma ^n_{\infty } }}$
. So by the isomorphism of sites
![]() $(V\times {\Gamma ^n_{\infty } })_{\mathrm {v\!+\!g}}$
and
$(V\times {\Gamma ^n_{\infty } })_{\mathrm {v\!+\!g}}$
and
![]() $(\widehat {V\times {\Gamma ^n_{\infty } }})_{\mathrm {v\!+\!g}}$
and Remark 5.25, the result holds in
$(\widehat {V\times {\Gamma ^n_{\infty } }})_{\mathrm {v\!+\!g}}$
and Remark 5.25, the result holds in
![]() $V\times {\Gamma ^n_{\infty } }$
. This proof actually shows that a basic
$V\times {\Gamma ^n_{\infty } }$
. This proof actually shows that a basic
![]() $\mathrm {v\!+\!g}$
-open subset of
$\mathrm {v\!+\!g}$
-open subset of
![]() $V\times {\Gamma ^n_{\infty } }$
is weakly
$V\times {\Gamma ^n_{\infty } }$
is weakly
![]() $\mathrm {v\!+\!g}$
-normal.
$\mathrm {v\!+\!g}$
-normal.
6 Cohomology, finiteness, invariance and vanishing
In this section, we deduce the Eilenberg-Steenrod axioms for the cohomology on the sites introduced in previous sections on definable subsets in
![]() ${\mathbf {\Gamma }_{\infty } },$
on definable subsets in ACVF and on their stable completions. We also show finiteness, invariance and vanishing results for these cohomologies.
${\mathbf {\Gamma }_{\infty } },$
on definable subsets in ACVF and on their stable completions. We also show finiteness, invariance and vanishing results for these cohomologies.
6.1 The Eilenberg-Steenrod axioms
The main work to show the Eilenberg-Steenrod axioms consists in showing the homotopy axiom. To achieve this goal, we will use the Vietoris-Begle theorem (Theorem 3.30) applied to the tilde
of the projection map. In particular, we need to verify the assumptions of the Vietoris-Begle theorem in this context. In
![]() ${\mathbf {\Gamma }_{\infty } }$
, these assumptions have been verified in the literature. For definable sets X and
${\mathbf {\Gamma }_{\infty } }$
, these assumptions have been verified in the literature. For definable sets X and
![]() $\widehat {X}$
in ACVF, some work is required.
$\widehat {X}$
in ACVF, some work is required.
We start with the following lemma whose proof is exactly the same as that of its o-minimal version given in [Reference Edmundo and Prelli28, Proposition 2.33]:
Lemma 6.1. Let
![]() $(X,{\mathcal {T}})$
be an object of
$(X,{\mathcal {T}})$
be an object of
![]() ${\mathfrak T}$
. Suppose that for every
${\mathfrak T}$
. Suppose that for every
![]() $\alpha \in \widetilde {X}$
, any chain of specialisations of
$\alpha \in \widetilde {X}$
, any chain of specialisations of
![]() $\alpha $
has finite length. If every
$\alpha $
has finite length. If every
![]() ${\mathcal {T}}$
-open subset of X is the union of finitely many
${\mathcal {T}}$
-open subset of X is the union of finitely many
![]() ${\mathcal {T}}$
-open subsets that are
${\mathcal {T}}$
-open subsets that are
![]() ${\mathcal {T}}$
-normal, then for every
${\mathcal {T}}$
-normal, then for every
![]() $\alpha \in \widetilde {X},$
there is an open, normal and constructible subset U of
$\alpha \in \widetilde {X},$
there is an open, normal and constructible subset U of
![]() $\widetilde {X}$
such that
$\widetilde {X}$
such that
![]() $\alpha \in U$
and
$\alpha \in U$
and
![]() $\alpha $
is closed in U.
$\alpha $
is closed in U.
![]() $\Box $
$\Box $
In the o-minimal context, the assumption of finiteness of chains of specialisations is verified in [Reference Edmundo, Jones and Peatfield22, Lemma 2.11]. We will now prove an analogue result in ACVF. Let us first make some general observations in this context.
Remark 6.2. Let V be an affine variety, say
![]() $V=\mathrm {Spec}(A)$
for
$V=\mathrm {Spec}(A)$
for
![]() $A=\mathbb {U}[T_1,\ldots ,T_n]/J$
, where J is an ideal of
$A=\mathbb {U}[T_1,\ldots ,T_n]/J$
, where J is an ideal of
![]() $\mathbb {U}[T_1,\ldots ,T_n]$
. Note that by quantifier elimination in ACVF, the set
$\mathbb {U}[T_1,\ldots ,T_n]$
. Note that by quantifier elimination in ACVF, the set
![]() $\widetilde {V}$
is in bijection with the set of pairs
$\widetilde {V}$
is in bijection with the set of pairs
![]() $(I,v)$
, where
$(I,v)$
, where
![]() $I\in V$
and v is a valuation on the fraction field
$I\in V$
and v is a valuation on the fraction field
![]() $\mathrm {Frac}(A/I)$
that extends
$\mathrm {Frac}(A/I)$
that extends
![]() $\mathrm {val}$
. Formally, the bijection sends
$\mathrm {val}$
. Formally, the bijection sends
![]() $p\mapsto (\mathrm {supp}(p),v_p)$
, where
$p\mapsto (\mathrm {supp}(p),v_p)$
, where
![]() $\mathrm {supp}(p):= \{f\in A: f(x)=0 \in p\}$
, and
$\mathrm {supp}(p):= \{f\in A: f(x)=0 \in p\}$
, and
![]() $v_p$
is determined by setting
$v_p$
is determined by setting
![]() $v_p(f/g)\geq 0$
if and only if the formula
$v_p(f/g)\geq 0$
if and only if the formula
![]() $\mathrm {val}(f(x))\geq \mathrm {val}(g(x))$
belongs to p (where
$\mathrm {val}(f(x))\geq \mathrm {val}(g(x))$
belongs to p (where
![]() $x=(x_1,\ldots , x_n)$
). We will denote the fraction field
$x=(x_1,\ldots , x_n)$
). We will denote the fraction field
![]() $\mathrm {Frac}(A/I)$
by
$\mathrm {Frac}(A/I)$
by
![]() $F_p$
and
$F_p$
and
![]() ${\mathcal {R}}_p$
denote the valuation ring of
${\mathcal {R}}_p$
denote the valuation ring of
![]() $F_p$
with respect to
$F_p$
with respect to
![]() $v_p$
.
$v_p$
.
As in Definition 3.4, recall that
![]() $\widetilde {V}$
is equipped with the topology generated by
$\widetilde {V}$
is equipped with the topology generated by
![]() $\widetilde {U}$
, where U is
$\widetilde {U}$
, where U is
![]() $\mathrm {v\!+\!g}$
-open in V. Given
$\mathrm {v\!+\!g}$
-open in V. Given
![]() $p,q\in \widetilde {V}$
, we write
$p,q\in \widetilde {V}$
, we write
![]() $p\prec q$
to state that p is a specialisation of q: that is, p belongs to the closure of
$p\prec q$
to state that p is a specialisation of q: that is, p belongs to the closure of
![]() $\{q\}$
. Note that if
$\{q\}$
. Note that if
![]() $p\prec q$
, then
$p\prec q$
, then
![]() $\mathrm {supp}(q)\subseteq \mathrm {supp}(p)$
as the set
$\mathrm {supp}(q)\subseteq \mathrm {supp}(p)$
as the set
![]() $\{ x\in V: \mathrm {val} (f(x))=\infty \}$
is
$\{ x\in V: \mathrm {val} (f(x))=\infty \}$
is
![]() $\mathrm {v\!+\!g}$
-closed. In particular, we may assume that
$\mathrm {v\!+\!g}$
-closed. In particular, we may assume that
![]() $F_p\subseteq F_q$
.
$F_p\subseteq F_q$
.
Lemma 6.3. Let V be a variety. Consider
![]() $\widetilde {V}$
with the topology generated by
$\widetilde {V}$
with the topology generated by
![]() $\widetilde {U}$
, where U is
$\widetilde {U}$
, where U is
![]() $\mathrm {v\!+\!g}$
-open in V. Then any chain of specialisations in
$\mathrm {v\!+\!g}$
-open in V. Then any chain of specialisations in
![]() $\widetilde {V}$
is bounded by
$\widetilde {V}$
is bounded by
![]() $\dim (V)$
.
$\dim (V)$
.
Proof. Since specialisation is local, it suffices to work with the case when V is affine. For affine V, let
![]() $A=\mathcal {O}_V(V)$
be the regular functions on V. Suppose that
$A=\mathcal {O}_V(V)$
be the regular functions on V. Suppose that
![]() $p\prec q$
for
$p\prec q$
for
![]() $p,q\in \widetilde {V}$
. As observed in the previous paragraph, we may suppose
$p,q\in \widetilde {V}$
. As observed in the previous paragraph, we may suppose
![]() $F_q\subseteq F_p$
. In addition, note that
$F_q\subseteq F_p$
. In addition, note that
![]() ${\mathcal {R}}_q\subseteq {\mathcal {R}}_p$
. Indeed, if there was
${\mathcal {R}}_q\subseteq {\mathcal {R}}_p$
. Indeed, if there was
![]() $f\in A$
such that
$f\in A$
such that
![]() $\mathrm {val}(f(x))\geq 0\in q$
but
$\mathrm {val}(f(x))\geq 0\in q$
but
![]() $\mathrm {val}(f(x))<0\in p$
, since the later formula defines a
$\mathrm {val}(f(x))<0\in p$
, since the later formula defines a
![]() $\mathrm {v\!+\!g}$
-open, we must have that
$\mathrm {v\!+\!g}$
-open, we must have that
![]() $\mathrm {val}(f(x))<0\in q$
, a contradiction. Hence, every chain
$\mathrm {val}(f(x))<0\in q$
, a contradiction. Hence, every chain
![]() $p_1\prec \cdots \prec p_n\prec p$
of specialisations of
$p_1\prec \cdots \prec p_n\prec p$
of specialisations of
![]() $p\in \widetilde {V}$
induces a chain of valued subfields
$p\in \widetilde {V}$
induces a chain of valued subfields
![]() $(F_p,{\mathcal {R}}_{p})\subseteq (F_{p_n},{\mathcal {R}}_{p_n})\subseteq \cdots \subseteq (F_{p_1},{\mathcal {R}}_{p_1})$
. By [Reference Engler and Prestel30, Corollary 3.4.6], the length of every such a chain is bounded by the dimension of V.
$(F_p,{\mathcal {R}}_{p})\subseteq (F_{p_n},{\mathcal {R}}_{p_n})\subseteq \cdots \subseteq (F_{p_1},{\mathcal {R}}_{p_1})$
. By [Reference Engler and Prestel30, Corollary 3.4.6], the length of every such a chain is bounded by the dimension of V.
Corollary 6.4. Let V be a variety, and let
![]() $X\subseteq V\times {\Gamma ^m_{\infty } }$
be a definable subset. Then any chain of specialisations in
$X\subseteq V\times {\Gamma ^m_{\infty } }$
be a definable subset. Then any chain of specialisations in
![]() $\widetilde {X}$
has finite length bounded by
$\widetilde {X}$
has finite length bounded by
![]() $\dim (V)+m$
. The same holds for
$\dim (V)+m$
. The same holds for
![]() $\widetilde {\widehat {X}}$
.
$\widetilde {\widehat {X}}$
.
Proof. Consider the commutative diagram

where the top arrow is
![]() $\widetilde {\mathrm {id} \times \mathrm {val}}$
, the bottom arrow is
$\widetilde {\mathrm {id} \times \mathrm {val}}$
, the bottom arrow is
![]() $\widetilde {\widehat {\mathrm {id} \times \mathrm {val}}}$
and the vertical arrows are homeomorphisms induced by isomorphisms of sites (Remark 3.8).
$\widetilde {\widehat {\mathrm {id} \times \mathrm {val}}}$
and the vertical arrows are homeomorphisms induced by isomorphisms of sites (Remark 3.8).
If there were a chain of specialisations in
![]() $\widetilde {V\times {\Gamma ^m_{\infty } }}$
of length
$\widetilde {V\times {\Gamma ^m_{\infty } }}$
of length
![]() $>\dim (V)+m$
, then there would be a chain of specialisations in
$>\dim (V)+m$
, then there would be a chain of specialisations in
![]() $\widetilde {\widehat {V\times {\Gamma ^m_{\infty } }}}$
of length
$\widetilde {\widehat {V\times {\Gamma ^m_{\infty } }}}$
of length
![]() $>\dim (V)+m.$
Since the bottom arrow has a section
$>\dim (V)+m.$
Since the bottom arrow has a section
![]() $\widetilde {s}: \widetilde {\widehat {V\times {\Gamma ^m_{\infty } }}} \to \widetilde {\widehat {V\times \mathbb {A} ^m}}$
, which is the tilde of an injective morphism of
$\widetilde {s}: \widetilde {\widehat {V\times {\Gamma ^m_{\infty } }}} \to \widetilde {\widehat {V\times \mathbb {A} ^m}}$
, which is the tilde of an injective morphism of
![]() $\widehat {\mathrm {v\!+\!g}}$
-sites (Lemma 5.29), we would also have a chain of specialisations of length
$\widehat {\mathrm {v\!+\!g}}$
-sites (Lemma 5.29), we would also have a chain of specialisations of length
![]() $>\dim (V)+m$
in
$>\dim (V)+m$
in
![]() $\widetilde {V\times \mathbb {A} ^m}$
, which contradicts Lemma 6.3.
$\widetilde {V\times \mathbb {A} ^m}$
, which contradicts Lemma 6.3.
Remark 6.5. One could improve the previous result by bounding the length of the specialisation chain by an appropriate notion of dimension for definable subsets of
![]() $\mathbb {A} ^n\times \Gamma _{\infty }^m$
. We would like to point out that a good candidate to play such a role was introduced by F. Martin in his PhD thesis [Reference Martin42], where he more generally defined a dimension function for subsets of
$\mathbb {A} ^n\times \Gamma _{\infty }^m$
. We would like to point out that a good candidate to play such a role was introduced by F. Martin in his PhD thesis [Reference Martin42], where he more generally defined a dimension function for subsets of
![]() $\mathbb {A} ^n\times \Gamma _{\infty }^m\times k^r$
.
$\mathbb {A} ^n\times \Gamma _{\infty }^m\times k^r$
.
In the o-minimal context, we know from Fact 4.16 that if
![]() $W\subseteq {\Gamma ^m_{\infty } }$
is definably normal and
$W\subseteq {\Gamma ^m_{\infty } }$
is definably normal and
![]() $[a,b]\subseteq {\Gamma _{\infty } }$
is a closed interval, then
$[a,b]\subseteq {\Gamma _{\infty } }$
is a closed interval, then
![]() $W\times [a,b]$
is also definably normal. In the ACVF context, we have:
$W\times [a,b]$
is also definably normal. In the ACVF context, we have:
Lemma 6.6. Let V be a variety. If W is a basic
![]() $\mathrm {v\!+\!g}$
-open subset of
$\mathrm {v\!+\!g}$
-open subset of
![]() $V\times {\Gamma ^m_{\infty } }$
and
$V\times {\Gamma ^m_{\infty } }$
and
![]() $[a, b]\subseteq {\Gamma _{\infty } }$
is a closed interval, then
$[a, b]\subseteq {\Gamma _{\infty } }$
is a closed interval, then
![]() $W\times [a,b]$
is weakly
$W\times [a,b]$
is weakly
![]() $\mathrm {v\!+\!g}$
-normal.
$\mathrm {v\!+\!g}$
-normal.
Proof. We have that the pullback of
![]() $W\times [a,b]$
under
$W\times [a,b]$
under
![]() $\mathrm {id} \times \mathrm {val} \colon V\times \mathbb {A} ^{m+1}\to V\times {\Gamma }_{\infty }^{m+1}$
is the intersection of the pullback of
$\mathrm {id} \times \mathrm {val} \colon V\times \mathbb {A} ^{m+1}\to V\times {\Gamma }_{\infty }^{m+1}$
is the intersection of the pullback of
![]() $W\times {\Gamma _{\infty } }$
and the pullback of
$W\times {\Gamma _{\infty } }$
and the pullback of
![]() $V\times {\Gamma ^m_{\infty } }\times [a,b]$
. The first pullback is a basic
$V\times {\Gamma ^m_{\infty } }\times [a,b]$
. The first pullback is a basic
![]() $\mathrm {v\!+\!g}$
-open subset of
$\mathrm {v\!+\!g}$
-open subset of
![]() $V\times \mathbb {A} ^{m+1},$
so it is weakly
$V\times \mathbb {A} ^{m+1},$
so it is weakly
![]() $\mathrm {v\!+\!g}$
-normal by Theorem 5.26. Since the second pullback is a
$\mathrm {v\!+\!g}$
-normal by Theorem 5.26. Since the second pullback is a
![]() $\mathrm {v\!+\!g}$
-closed subset
$\mathrm {v\!+\!g}$
-closed subset
![]() $V\times \mathbb {A} ^{m+1}$
, it follows that
$V\times \mathbb {A} ^{m+1}$
, it follows that
![]() $(\mathrm {id} \times \mathrm {val})^{-1}(W\times [a,b])$
is weakly
$(\mathrm {id} \times \mathrm {val})^{-1}(W\times [a,b])$
is weakly
![]() $\mathrm {v\!+\!g}$
-normal (being a
$\mathrm {v\!+\!g}$
-normal (being a
![]() $\mathrm {v\!+\!g}$
-closed subset of a weakly
$\mathrm {v\!+\!g}$
-closed subset of a weakly
![]() $\mathrm {v\!+\!g}$
-normal set). From Lemmas 5.29 and 5.30 and Remark 5.25, it follows that
$\mathrm {v\!+\!g}$
-normal set). From Lemmas 5.29 and 5.30 and Remark 5.25, it follows that
![]() $W\times [a,b]$
is weakly
$W\times [a,b]$
is weakly
![]() $\mathrm {v\!+\!g}$
-normal.
$\mathrm {v\!+\!g}$
-normal.
In the o-minimal context, since
![]() $[a,b]$
is definably compact, the definable map
$[a,b]$
is definably compact, the definable map
![]() $[a,b]\to \mathrm {pt}$
is definably proper ([Reference Edmundo, Mamino and Prelli23, Definition 3.10 and Remark 3.11]), and since
$[a,b]\to \mathrm {pt}$
is definably proper ([Reference Edmundo, Mamino and Prelli23, Definition 3.10 and Remark 3.11]), and since
![]() ${\mathbf {\Sigma }}$
has definable Skolem functions, the map
${\mathbf {\Sigma }}$
has definable Skolem functions, the map
![]() $[a,b]\to \mathrm {pt}$
is proper in
$[a,b]\to \mathrm {pt}$
is proper in
![]() $\mathrm {Def}$
([Reference Edmundo, Mamino and Prelli23, Definition 3.3 and Theorem 3.15]). Hence if X is a definable subset of
$\mathrm {Def}$
([Reference Edmundo, Mamino and Prelli23, Definition 3.3 and Theorem 3.15]). Hence if X is a definable subset of
![]() ${\Gamma ^n_{\infty } },$
then
${\Gamma ^n_{\infty } },$
then
![]() $\pi \colon X\times [a,b]\longrightarrow X$
maps closed definable subsets to closed definable subsets. In the ACVF context, we have:
$\pi \colon X\times [a,b]\longrightarrow X$
maps closed definable subsets to closed definable subsets. In the ACVF context, we have:
Lemma 6.7. Let V be a variety. Let X be a definable subset of
![]() $V\times {\Gamma ^n_{\infty } }$
and
$V\times {\Gamma ^n_{\infty } }$
and
![]() $[a,b]\subseteq {\Gamma _{\infty } }$
be a closed interval. Then the projection
$[a,b]\subseteq {\Gamma _{\infty } }$
be a closed interval. Then the projection
![]() $\pi \colon X\times [a, b]\to X$
is
$\pi \colon X\times [a, b]\to X$
is
![]() $\mathrm {v\!+\!g}$
-closed: that is, maps
$\mathrm {v\!+\!g}$
-closed: that is, maps
![]() $\mathrm {v\!+\!g}$
-closed subsets into
$\mathrm {v\!+\!g}$
-closed subsets into
![]() $\mathrm {v\!+\!g}$
-closed subsets.
$\mathrm {v\!+\!g}$
-closed subsets.
Proof. Let
![]() $C\subseteq X\times [a,b]$
be a
$C\subseteq X\times [a,b]$
be a
![]() $\mathrm {v\!+\!g}$
-closed subset. Then
$\mathrm {v\!+\!g}$
-closed subset. Then
![]() $\widehat {C}$
is a closed relatively pro-definable subset of
$\widehat {C}$
is a closed relatively pro-definable subset of
![]() $\widehat {X\times [a,b]}$
. It is enough to show that
$\widehat {X\times [a,b]}$
. It is enough to show that
![]() $\widehat {\pi (C)}$
is closed. If it is not closed, then by [Reference Hrushovski and Loeser35, Proposition 4.2.13], there is a definable type
$\widehat {\pi (C)}$
is closed. If it is not closed, then by [Reference Hrushovski and Loeser35, Proposition 4.2.13], there is a definable type
![]() $\mathfrak {p}$
on
$\mathfrak {p}$
on
![]() $\widehat {X}$
concentrating on
$\widehat {X}$
concentrating on
![]() $\widehat {\pi (C)}$
with limit p in the closure of
$\widehat {\pi (C)}$
with limit p in the closure of
![]() $\widehat {\pi (C)}$
in
$\widehat {\pi (C)}$
in
![]() $\widehat {X}$
such that
$\widehat {X}$
such that
![]() $p\notin \widehat {\pi (C)}$
. Applying [Reference Hrushovski and Loeser35, Lemma 4.2.6 (2)] twice to the surjective definable map
$p\notin \widehat {\pi (C)}$
. Applying [Reference Hrushovski and Loeser35, Lemma 4.2.6 (2)] twice to the surjective definable map
![]() $\pi \colon C\to \pi (C)$
, we have that there is a definable type
$\pi \colon C\to \pi (C)$
, we have that there is a definable type
![]() $\mathfrak {q}$
on
$\mathfrak {q}$
on
![]() $\widehat {X\times [a,b]}$
concentrating on
$\widehat {X\times [a,b]}$
concentrating on
![]() $\widehat {C}$
such that
$\widehat {C}$
such that
![]() $\widehat {\pi }_{\ast }(\mathfrak {q})=\mathfrak {p}$
. Since
$\widehat {\pi }_{\ast }(\mathfrak {q})=\mathfrak {p}$
. Since
![]() $\widehat {X\times [a,b]}\cong \widehat {X}\times [a,b]$
, the topology is the product topology and definable types on
$\widehat {X\times [a,b]}\cong \widehat {X}\times [a,b]$
, the topology is the product topology and definable types on
![]() $[a,b]$
have limits,
$[a,b]$
have limits,
![]() $\mathfrak {q}$
must have a limit q in
$\mathfrak {q}$
must have a limit q in
![]() $\widehat {X\times [a,b]}$
(namely, the tensor product of the limits of the corresponding projections). By [Reference Hrushovski and Loeser35, Lemma 4.2.4],
$\widehat {X\times [a,b]}$
(namely, the tensor product of the limits of the corresponding projections). By [Reference Hrushovski and Loeser35, Lemma 4.2.4],
![]() $q\in \widehat {C}$
, so
$q\in \widehat {C}$
, so
![]() $p=\widehat {\pi }(q)\in \widehat {\pi (C)}$
.
$p=\widehat {\pi }(q)\in \widehat {\pi (C)}$
.
Theorem 6.8 (Homotopy axiom in stable completions).
Let V be a variety. Let
![]() $X\subseteq V\times {\Gamma ^m_{\infty } }$
be a
$X\subseteq V\times {\Gamma ^m_{\infty } }$
be a
![]() $\mathrm {v\!+\!g}$
-locally closed subset, and let
$\mathrm {v\!+\!g}$
-locally closed subset, and let
![]() ${\mathcal {F}}\in \mathrm {Mod} (A_{\widehat {X}_{\widehat {\mathrm {v\!+\!g}}}})$
. Let
${\mathcal {F}}\in \mathrm {Mod} (A_{\widehat {X}_{\widehat {\mathrm {v\!+\!g}}}})$
. Let
![]() $\Psi $
be a family of
$\Psi $
be a family of
![]() $\widehat {\mathrm {v\!+\!g}}$
-supports on
$\widehat {\mathrm {v\!+\!g}}$
-supports on
![]() $\widehat {X}$
. Let
$\widehat {X}$
. Let
![]() $[a,b]\subseteq [0,\infty ]$
be a closed interval,
$[a,b]\subseteq [0,\infty ]$
be a closed interval,
![]() $\pi \colon X\times [a,b]\to X$
be the projection, and for
$\pi \colon X\times [a,b]\to X$
be the projection, and for
![]() $d\in [a,b]$
, let
$d\in [a,b]$
, let
be the continuous definable map given by
![]() $i_d(x)=(x,d)$
for all
$i_d(x)=(x,d)$
for all
![]() $x\in X$
. Then
$x\in X$
. Then
for all
![]() $n\geq 0$
.
$n\geq 0$
.
Proof. The homotopy axiom will follow once we show that the projection map
![]() $\pi \colon X\times [a,b]\longrightarrow X$
induces an isomorphism
$\pi \colon X\times [a,b]\longrightarrow X$
induces an isomorphism
since by functoriality, we obtain
for all
![]() $n\geq 0$
. Equivalently, we need to show that
$n\geq 0$
. Equivalently, we need to show that
is an isomorphism. For this, we need to verify the hypothesis of the Vietoris-Begle theorem (Theorem 3.30).
By Lemma 6.7 (and the fact that
![]() $\widehat {\pi (Z)}=\widehat {\pi }(\widehat {Z})$
([Reference Hrushovski and Loeser35, Lemma 4.2.6])),
$\widehat {\pi (Z)}=\widehat {\pi }(\widehat {Z})$
([Reference Hrushovski and Loeser35, Lemma 4.2.6])),
![]() $\widehat {\pi }$
maps closed subsets to closed subsets. It follows that
$\widehat {\pi }$
maps closed subsets to closed subsets. It follows that
![]() $\widetilde {\widehat {\pi }}$
maps closed constructible subset to closed (constructible) subsets.
$\widetilde {\widehat {\pi }}$
maps closed constructible subset to closed (constructible) subsets.
Let
![]() $\alpha \in \widetilde {\widehat {X}}$
. Given Corollaries 6.4 and 5.31 together with Remark 5.25, it follows from Lemma 6.1 that there is an open, normal constructible subset U of
$\alpha \in \widetilde {\widehat {X}}$
. Given Corollaries 6.4 and 5.31 together with Remark 5.25, it follows from Lemma 6.1 that there is an open, normal constructible subset U of
![]() $\widetilde {\widehat {X}}$
such that
$\widetilde {\widehat {X}}$
such that
![]() $\alpha \in U$
and
$\alpha \in U$
and
![]() $\alpha $
is closed in U. Furthermore, we may assume that U is of the form
$\alpha $
is closed in U. Furthermore, we may assume that U is of the form
![]() $\widetilde {\widehat {W}}$
, where W is a basic
$\widetilde {\widehat {W}}$
, where W is a basic
![]() $\mathrm {v\!+\!g}$
-open subset of X. From Lemma 6.6, it follows that
$\mathrm {v\!+\!g}$
-open subset of X. From Lemma 6.6, it follows that
![]() $W\times [a,b]$
is weakly
$W\times [a,b]$
is weakly
![]() $\mathrm {v\!+\!g}$
-normal, and hence, by Remark 5.25,
$\mathrm {v\!+\!g}$
-normal, and hence, by Remark 5.25,
![]() $\widehat {W\times [a,b]}\simeq \widehat {W}\times [a,b]$
is
$\widehat {W\times [a,b]}\simeq \widehat {W}\times [a,b]$
is
![]() $\widehat {\mathrm {v\!+\!g}}$
-normal. Since
$\widehat {\mathrm {v\!+\!g}}$
-normal. Since
![]() $\widetilde {\widehat {\pi }}^{-1}(\widetilde {\widehat {W}})=\widetilde {\widehat {\pi }^{-1}(\widehat {W})}=\widetilde {\widehat {W}\times [a,b]},$
this set is normal and constructible by Proposition 3.12.
$\widetilde {\widehat {\pi }}^{-1}(\widetilde {\widehat {W}})=\widetilde {\widehat {\pi }^{-1}(\widehat {W})}=\widetilde {\widehat {W}\times [a,b]},$
this set is normal and constructible by Proposition 3.12.
Since
![]() $\widehat {\pi ^{-1}(V)}=\widehat {\pi }^{-1}(\widehat {V})$
, we have a commutative diagram
$\widehat {\pi ^{-1}(V)}=\widehat {\pi }^{-1}(\widehat {V})$
, we have a commutative diagram

of morphisms of sites that induces a commutative diagram

where the vertical arrows are homeomorphisms induced by isomorphisms of sites (Remark 3.8). It follows that
![]() $\widetilde {\widehat {\pi }}^{-1}(\alpha )$
is homeomorphic to
$\widetilde {\widehat {\pi }}^{-1}(\alpha )$
is homeomorphic to
![]() $\widetilde {\pi }^{-1}(\beta )$
for some
$\widetilde {\pi }^{-1}(\beta )$
for some
![]() $\beta \in \widetilde {X}$
. On the other hand, as in the proof of [Reference Edmundo, Jones and Peatfield22, Claim 4.5], and since the value group
$\beta \in \widetilde {X}$
. On the other hand, as in the proof of [Reference Edmundo, Jones and Peatfield22, Claim 4.5], and since the value group
![]() ${\mathbf {\Gamma }_{\infty } }$
is stably embedded,
${\mathbf {\Gamma }_{\infty } }$
is stably embedded,
![]() $\widetilde {\pi }^{-1}(\beta )$
is homeomorphic to
$\widetilde {\pi }^{-1}(\beta )$
is homeomorphic to
![]() $\widetilde {[a,b]({\mathbf {\Sigma }} ')}$
, where
$\widetilde {[a,b]({\mathbf {\Sigma }} ')}$
, where
![]() ${\mathbf {\Sigma }} '$
is the definable closure of
${\mathbf {\Sigma }} '$
is the definable closure of
![]() ${\Sigma } \cup \{b\}$
with b an element realising the type
${\Sigma } \cup \{b\}$
with b an element realising the type
![]() $\beta$
, and therefore,
$\beta$
, and therefore,
![]() $\widetilde {\pi }^{-1}({\beta })$
is connected and
$\widetilde {\pi }^{-1}({\beta })$
is connected and
![]() $H^q(\widetilde {\pi }^{-1}({\beta }); \widetilde {\pi }^{-1}\widetilde {{\mathcal {F}}}_{|\widetilde {\pi }^{-1}({\beta })})=0$
for all
$H^q(\widetilde {\pi }^{-1}({\beta }); \widetilde {\pi }^{-1}\widetilde {{\mathcal {F}}}_{|\widetilde {\pi }^{-1}({\beta })})=0$
for all
![]() $q>0$
. So we conclude that
$q>0$
. So we conclude that
![]() $\widetilde {\widehat {\pi }}^{-1}(\alpha )$
is connected and acyclic as required.
$\widetilde {\widehat {\pi }}^{-1}(\alpha )$
is connected and acyclic as required.
Corollary 6.9 (Homotopy axiom in ACVF).
Let V be a variety. Let
![]() $X\subseteq V\times {\Gamma ^m_{\infty } }$
be a
$X\subseteq V\times {\Gamma ^m_{\infty } }$
be a
![]() $\mathrm {v\!+\!g}$
-locally closed subset, and let
$\mathrm {v\!+\!g}$
-locally closed subset, and let
![]() ${\mathcal {F}}\in \mathrm {Mod} (A_{X_{\mathrm {v\!+\!g}}})$
. Let
${\mathcal {F}}\in \mathrm {Mod} (A_{X_{\mathrm {v\!+\!g}}})$
. Let
![]() $\Psi $
a family of
$\Psi $
a family of
![]() $\mathrm {v\!+\!g}$
-supports on X. Let
$\mathrm {v\!+\!g}$
-supports on X. Let
![]() $[a,b]\subseteq [0,\infty ]$
be a closed interval, let
$[a,b]\subseteq [0,\infty ]$
be a closed interval, let
![]() $\pi \colon X\times [a,b]\to X$
be the projection, and, for
$\pi \colon X\times [a,b]\to X$
be the projection, and, for
![]() $d\in [a,b]$
, let
$d\in [a,b]$
, let
be the continuous definable map given by
![]() $i_d(x)=(x,d)$
for all
$i_d(x)=(x,d)$
for all
![]() $x\in X$
. Then
$x\in X$
. Then
for all
![]() $n\geq 0$
.
$n\geq 0$
.
Proof. As explained in the previous proof, the homotopy axiom will follow once we show that the projection map
![]() $\pi \colon X\times [a,b]\longrightarrow X$
induces an isomorphism
$\pi \colon X\times [a,b]\longrightarrow X$
induces an isomorphism
But this follows from the isomorphism
proven in Theorem 6.8 and the commutative diagram

of morphisms of sites, with the vertical arrows being isomorphisms of sites.
Using Theorem 4.28 and the
![]() ${\mathbf {\Gamma }_{\infty } }$
analogues of Lemmas 6.3, 6.6 and 6.7 mentioned above, arguing as in the proof of Theorem 6.8, we obtain:
${\mathbf {\Gamma }_{\infty } }$
analogues of Lemmas 6.3, 6.6 and 6.7 mentioned above, arguing as in the proof of Theorem 6.8, we obtain:
Theorem 6.10 (Homotopy axiom in
 ${\mathbf {\Gamma }_{\infty } }$
).
${\mathbf {\Gamma }_{\infty } }$
).
Let
![]() ${\mathbf {\Gamma }}=({\Gamma }, <, +,\ldots )$
be an arbitrary o-minimal expansion of an ordered group. Suppose that
${\mathbf {\Gamma }}=({\Gamma }, <, +,\ldots )$
be an arbitrary o-minimal expansion of an ordered group. Suppose that
![]() $X\subseteq {\Gamma ^m_{\infty } }$
is a definably locally closed set and
$X\subseteq {\Gamma ^m_{\infty } }$
is a definably locally closed set and
![]() ${\mathcal {F}}\in \mathrm {Mod} (A_{X_{\mathrm {def}}})$
. Let
${\mathcal {F}}\in \mathrm {Mod} (A_{X_{\mathrm {def}}})$
. Let
![]() $\Psi $
be a family of definable supports on X. Let
$\Psi $
be a family of definable supports on X. Let
![]() $[a,b]\subseteq [0,\infty ]$
be a closed interval,
$[a,b]\subseteq [0,\infty ]$
be a closed interval,
![]() $\pi \colon X\times [a,b]\to X$
the projection and, for
$\pi \colon X\times [a,b]\to X$
the projection and, for
![]() $d\in [a,b]$
,
$d\in [a,b]$
,
be the continuous definable map given by
![]() $i_d(x)=(x,d)$
for all
$i_d(x)=(x,d)$
for all
![]() $x\in X$
. Then
$x\in X$
. Then
for all
![]() $n\geq 0$
.
$n\geq 0$
.
Theorem 6.11. The sheaf cohomology associated to
-
(1) the category of definable sets in
 ${\mathbf {\Gamma }_{\infty } }$
with their associated o-minimal site,
${\mathbf {\Gamma }_{\infty } }$
with their associated o-minimal site, -
(2) the full subcategory of definable sets in
 $\mathrm {ACVF}$
with their associated
$\mathrm {ACVF}$
with their associated
 $\mathrm {v\!+\!g}$
-site and
$\mathrm {v\!+\!g}$
-site and -
(3) the category of stable completions with their associated
 $\widehat {\mathrm {v\!+\!g}}$
-site
$\widehat {\mathrm {v\!+\!g}}$
-site
satisfies the Eilenberg-Steenrod axioms.
Proof. The homotopy axiom corresponds to Theorem 6.10 for (1), to Corollary 6.9 for (2) and to Theorem 6.8 for (3). For all (1)–(3), the remaining axioms follow by standard arguments. Indeed, once we apply the tilde functor in each case, the proofs of the exactness ([Reference Bredon14, Chapter II, Section 12, (22)]) and excision axioms ([Reference Bredon14, Chapter II, Section 12, 12.8 or 12.9]) are purely algebraic. The dimension axiom is also immediate.
Remark 6.12. From the Eilenberg-Steenrod axioms for cohomology, one obtains as usual the exactness for triples ([Reference Bredon14, Chapter II, Section 12, (24)]) and the Mayer-Vietoris long exact sequence ([Reference Bredon14, Chapter II, Section 13, (32)]).
6.2 Finiteness and invariance results in
 ${\mathbf {\Gamma }_{\infty } }$
${\mathbf {\Gamma }_{\infty } }$
Here we will show finiteness and invariance results for o-minimal cohomology with definably compact supports of definably locally closed subsets of
![]() ${\Gamma ^m_{\infty } }$
. Using Hrushovski and Loeser’s main theorem ([Reference Hrushovski and Loeser35, Theorem 11.1.1]), we will deduce in the next subsection finiteness and invariance results for cohomology in ACVF and in stable completions.
${\Gamma ^m_{\infty } }$
. Using Hrushovski and Loeser’s main theorem ([Reference Hrushovski and Loeser35, Theorem 11.1.1]), we will deduce in the next subsection finiteness and invariance results for cohomology in ACVF and in stable completions.
For the finiteness and invariance results in
![]() ${\mathbf {\Gamma }_{\infty } }$
, we first show that the arguments from [Reference Berarducci and Fornasiero7] for
${\mathbf {\Gamma }_{\infty } }$
, we first show that the arguments from [Reference Berarducci and Fornasiero7] for
![]() ${\mathbf {\Gamma }} =({\Gamma }, < , +, \ldots )$
and for definably compact sets can be extended to
${\mathbf {\Gamma }} =({\Gamma }, < , +, \ldots )$
and for definably compact sets can be extended to
![]() ${\mathbf {\Gamma }_{\infty } }$
and to definably locally closed sets with only minor modifications. We include the details in the main technical lemma (Lemma 6.15) and refer the reader to [Reference Berarducci and Fornasiero7] for the other results that simply follow from the Eilenberg-Steenrod axioms. Concerning invariance, the extension to arbitrary sheaves adapts techniques from [Reference Edmundo and Prelli26], and we include the details as the same argument will be used in the ACVF case.
${\mathbf {\Gamma }_{\infty } }$
and to definably locally closed sets with only minor modifications. We include the details in the main technical lemma (Lemma 6.15) and refer the reader to [Reference Berarducci and Fornasiero7] for the other results that simply follow from the Eilenberg-Steenrod axioms. Concerning invariance, the extension to arbitrary sheaves adapts techniques from [Reference Edmundo and Prelli26], and we include the details as the same argument will be used in the ACVF case.
Below, we let L be an A-module, where A is a commutative ring with unit.
In [Reference Berarducci and Fornasiero7, Lemma 3.2], it is shown that for every bounded cell in
![]() ${\Gamma ^m}$
, there is a deformation retraction of C onto a cell of strictly lower dimension via a
${\Gamma ^m}$
, there is a deformation retraction of C onto a cell of strictly lower dimension via a
![]() ${\Gamma }$
-definable homotopy. As observed in [Reference Berarducci and Fornasiero7], the proof extends to
${\Gamma }$
-definable homotopy. As observed in [Reference Berarducci and Fornasiero7], the proof extends to
![]() ${\mathbf {\Gamma }_{\infty } }$
.
${\mathbf {\Gamma }_{\infty } }$
.
Lemma 6.13. If
![]() $C\subseteq [0,\infty ]^m$
is a cell of dimension
$C\subseteq [0,\infty ]^m$
is a cell of dimension
![]() $n>0,$
then there is a deformation retraction of C onto a cell of strictly lower dimension. So by induction, every cell in
$n>0,$
then there is a deformation retraction of C onto a cell of strictly lower dimension. So by induction, every cell in
![]() $[0,\infty ]^m$
is
$[0,\infty ]^m$
is
![]() ${\mathbf {\Gamma }_{\infty } }$
-definably contractible to a point.
${\mathbf {\Gamma }_{\infty } }$
-definably contractible to a point.
Proof. If C is the graph of a function, we can reason by induction on m. So assume
![]() $C=(f,g)_B$
. If
$C=(f,g)_B$
. If
![]() $g<\infty $
and C is of maximal dimension, then
$g<\infty $
and C is of maximal dimension, then
![]() $C\subseteq {\Gamma ^m}$
, and we can apply [Reference Berarducci and Fornasiero7, Lemma 3.2]. If
$C\subseteq {\Gamma ^m}$
, and we can apply [Reference Berarducci and Fornasiero7, Lemma 3.2]. If
![]() $g<\infty $
and C is not of maximal dimension, then one can apply induction. If
$g<\infty $
and C is not of maximal dimension, then one can apply induction. If
![]() $g=\infty $
, let
$g=\infty $
, let
![]() $h=f+1$
. Then
$h=f+1$
. Then
![]() $f<h<g$
, and the
$f<h<g$
, and the
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable map given
${\mathbf {\Gamma }_{\infty } }$
-definable map given
![]() $H\colon [0, \infty ]\times C\to C$
by
$H\colon [0, \infty ]\times C\to C$
by
 $$\begin{align*}H(t, (x,y))=\begin{cases} (x, h(x)-t), &\text{ if } y< h(x)-t\\ (x,y), &\text{ if } h(x)-t \le y\le h(x)+t\\ (x, h(x)+t), &\text{ if } y> h(x)+t \end{cases} \end{align*}$$
$$\begin{align*}H(t, (x,y))=\begin{cases} (x, h(x)-t), &\text{ if } y< h(x)-t\\ (x,y), &\text{ if } h(x)-t \le y\le h(x)+t\\ (x, h(x)+t), &\text{ if } y> h(x)+t \end{cases} \end{align*}$$
is a deformation retract of C onto the cell
![]() $\Gamma (h)$
.
$\Gamma (h)$
.
As observed after the proof of [Reference Berarducci and Fornasiero7, Corollary 3.3] that result (for bounded cell in
![]() ${\Gamma ^n}$
) extends to
${\Gamma ^n}$
) extends to
![]() ${\mathbf {\Gamma }_{\infty } }$
due to Lemma 6.13 and the homotopy axiom (Theorem 6.10), recall that cells are definably locally closed (Remark 4.12):
${\mathbf {\Gamma }_{\infty } }$
due to Lemma 6.13 and the homotopy axiom (Theorem 6.10), recall that cells are definably locally closed (Remark 4.12):
Lemma 6.14. Let
![]() $C\subseteq [0,\infty ]^m$
be a cell. Then C is acyclic: that is,
$C\subseteq [0,\infty ]^m$
be a cell. Then C is acyclic: that is,
![]() $H^p(C;L_C)=0$
for
$H^p(C;L_C)=0$
for
![]() $p>0$
and
$p>0$
and
![]() $H^0(C; L_C)=L$
.
$H^0(C; L_C)=L$
.
![]() $\Box $
$\Box $
We also have the analogue of [Reference Berarducci and Fornasiero7, Lemma 7.1] with small modifications in the construction:
Lemma 6.15. Let
![]() $C\subseteq [0,\infty ]^m$
be a cell of dimension r. There is a
$C\subseteq [0,\infty ]^m$
be a cell of dimension r. There is a
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable family
${\mathbf {\Gamma }_{\infty } }$
-definable family
![]() $\{C_{(t,s)} : 0<t,s<\infty \}$
of closed and bounded subsets
$\{C_{(t,s)} : 0<t,s<\infty \}$
of closed and bounded subsets
![]() $C_{(t,s)} \subseteq C$
such that:
$C_{(t,s)} \subseteq C$
such that:
-
(1)
 $C = \bigcup _{(t,s)}C_{(t,s)}$
.
$C = \bigcup _{(t,s)}C_{(t,s)}$
. -
(2) If
 $r>0$
and
$r>0$
and
 $0 < t' < t<\frac {s}{2}<s<s',$
then
$0 < t' < t<\frac {s}{2}<s<s',$
then
 $C_{(t,s)} \subseteq C_{(t',s')}$
, and this inclusion induces an isomorphism
$C_{(t,s)} \subseteq C_{(t',s')}$
, and this inclusion induces an isomorphism  $$\begin{align*}H^{p}(C \backslash C_{(t,s)}; L_C) \simeq H^{p}(C \backslash C_{(t',s')}; L_C). \end{align*}$$
$$\begin{align*}H^{p}(C \backslash C_{(t,s)}; L_C) \simeq H^{p}(C \backslash C_{(t',s')}; L_C). \end{align*}$$
-
(3) If
 $r>0$
, then the o-minimal cohomology of
$r>0$
, then the o-minimal cohomology of
 $C \backslash C_{(t,s)}$
is given by where
$C \backslash C_{(t,s)}$
is given by where $$ \begin{align*} H^{p}(C \backslash C_{(t,s)}; L_C) = \begin{cases} L ^{1+\chi _{1}(r)}\qquad \mathrm{if} \qquad p\in \{0, r-1\}\\ \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \\ 0\qquad \,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\, \, \mathrm{if} \qquad p\notin \{0, r-1\} \end{cases} \end{align*} $$
$$ \begin{align*} H^{p}(C \backslash C_{(t,s)}; L_C) = \begin{cases} L ^{1+\chi _{1}(r)}\qquad \mathrm{if} \qquad p\in \{0, r-1\}\\ \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \\ 0\qquad \,\,\,\,\,\,\, \,\,\,\,\,\,\,\,\,\,\, \, \mathrm{if} \qquad p\notin \{0, r-1\} \end{cases} \end{align*} $$
 $\chi _1\colon {\mathbb Z}\to \{0,1\}$
is the characteristic function of the subset
$\chi _1\colon {\mathbb Z}\to \{0,1\}$
is the characteristic function of the subset
 $\{1\}$
.
$\{1\}$
.
-
(4) If
 $K\subseteq C$
is a definably compact subset, the there are
$K\subseteq C$
is a definably compact subset, the there are
 $0<t,s$
such that
$0<t,s$
such that
 $K\subseteq C_{(t,s)}$
.
$K\subseteq C_{(t,s)}$
.
Proof. We define the definable family
![]() $\{C_{(t,s)} : 0<t, s <\infty \}$
by induction on
$\{C_{(t,s)} : 0<t, s <\infty \}$
by induction on
![]() $l\in \{1,\ldots , m-1\}$
and the definition of the
$l\in \{1,\ldots , m-1\}$
and the definition of the
![]() ${\mathbf {\Gamma }_{\infty } }$
-cell C in the following way:
${\mathbf {\Gamma }_{\infty } }$
-cell C in the following way:
-
• If
 $l=1$
and C is a singleton
$l=1$
and C is a singleton
 $\{d\}$
in
$\{d\}$
in
 ${\Gamma _{\infty } }$
, we define
${\Gamma _{\infty } }$
, we define
 $C_{(t,s)}=C$
. Clearly
$C_{(t,s)}=C$
. Clearly
 $C_{(t,s)}$
is a closed and bounded subset.
$C_{(t,s)}$
is a closed and bounded subset. -
• If
 $l= 1$
and
$l= 1$
and
 $C = (d, e)\subseteq {\Gamma _{\infty } },$
then where
$C = (d, e)\subseteq {\Gamma _{\infty } },$
then where $$ \begin{align*} C_{(t,s)} = \begin{cases} [d + \gamma (t,s), e -\gamma (t,s)]\quad \quad \quad \quad \quad \quad \textrm{if}\quad e< \infty\\ \,\, \\ [d+\gamma (t,s), (d+s)-\gamma(t,s)] \quad \quad \quad \,\,\, \textrm{otherwise} \end{cases} \end{align*} $$
(in this way
$$ \begin{align*} C_{(t,s)} = \begin{cases} [d + \gamma (t,s), e -\gamma (t,s)]\quad \quad \quad \quad \quad \quad \textrm{if}\quad e< \infty\\ \,\, \\ [d+\gamma (t,s), (d+s)-\gamma(t,s)] \quad \quad \quad \,\,\, \textrm{otherwise} \end{cases} \end{align*} $$
(in this way $$ \begin{align*} \gamma (t,s) = \begin{cases} \min\{\frac{e-d}{2}, t\} \quad \quad \quad \textrm{if}\quad e< \infty\\ \,\, \\ \min \{\frac{s}{2}, t\} \quad \quad \quad \quad \textrm{otherwise} \end{cases} \end{align*} $$
$$ \begin{align*} \gamma (t,s) = \begin{cases} \min\{\frac{e-d}{2}, t\} \quad \quad \quad \textrm{if}\quad e< \infty\\ \,\, \\ \min \{\frac{s}{2}, t\} \quad \quad \quad \quad \textrm{otherwise} \end{cases} \end{align*} $$
 $C_{(t,s)}$
is non empty). Clearly
$C_{(t,s)}$
is non empty). Clearly
 $C_{(t,s)}$
is a closed and bounded subset.
$C_{(t,s)}$
is a closed and bounded subset.
-
• If
 $l> 1$
and
$l> 1$
and
 $C = \Gamma (f)$
, where
$C = \Gamma (f)$
, where
 $B\subseteq [0,\infty ]^{l}$
is
$B\subseteq [0,\infty ]^{l}$
is
 ${\mathbf {\Gamma }_{\infty } }$
-cell. By induction,
${\mathbf {\Gamma }_{\infty } }$
-cell. By induction,
 $B_{(t,s)}$
is defined and is a closed and bounded subset. We put
$B_{(t,s)}$
is defined and is a closed and bounded subset. We put
 $C_{(t,s)}=\Gamma (f_{|B_{(t,s)}})$
. Clearly
$C_{(t,s)}=\Gamma (f_{|B_{(t,s)}})$
. Clearly
 $C_{(t,s)}$
is a closed and bounded subset.
$C_{(t,s)}$
is a closed and bounded subset. -
• If
 $l> 1$
and
$l> 1$
and
 $C = (f, g)_{B}$
, where
$C = (f, g)_{B}$
, where
 $B\subseteq [0,\infty ]^{l}$
is
$B\subseteq [0,\infty ]^{l}$
is
 ${\mathbf {\Gamma }_{\infty } }$
-cell and
${\mathbf {\Gamma }_{\infty } }$
-cell and
 $f<g$
. By induction,
$f<g$
. By induction,
 $B_{(t,s)}$
is defined and is a closed and bounded subset. Recall that either
$B_{(t,s)}$
is defined and is a closed and bounded subset. Recall that either
 $g<\infty $
or
$g<\infty $
or
 $g=\infty $
. We put where
$g=\infty $
. We put where $$ \begin{align*} C_{(t,s)} = \begin{cases} [f +\gamma (t,s), g - \gamma (t,s)]_{B_{(t,s)}}\quad \quad \quad \quad \quad \quad \textrm{if}\quad g< \infty\\ \,\, \\ [f+\gamma (t,s), (f+s)-\gamma(t,s)]_{B_{(t,s)}} \quad \quad \quad \,\, \textrm{otherwise} \end{cases} \end{align*} $$
By induction,
$$ \begin{align*} C_{(t,s)} = \begin{cases} [f +\gamma (t,s), g - \gamma (t,s)]_{B_{(t,s)}}\quad \quad \quad \quad \quad \quad \textrm{if}\quad g< \infty\\ \,\, \\ [f+\gamma (t,s), (f+s)-\gamma(t,s)]_{B_{(t,s)}} \quad \quad \quad \,\, \textrm{otherwise} \end{cases} \end{align*} $$
By induction, $$ \begin{align*} \gamma (t,s) = \begin{cases} \min\{\frac{g-f}{2}, t\} \quad \quad \quad \textrm{if}\quad g< \infty\\ \,\, \\ \min \{\frac{s}{2}, t\} \quad \quad \quad \quad \textrm{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} \gamma (t,s) = \begin{cases} \min\{\frac{g-f}{2}, t\} \quad \quad \quad \textrm{if}\quad g< \infty\\ \,\, \\ \min \{\frac{s}{2}, t\} \quad \quad \quad \quad \textrm{otherwise.} \end{cases} \end{align*} $$
 $B_{(t,s)}$
is a closed and bounded subset of B. Also, for each
$B_{(t,s)}$
is a closed and bounded subset of B. Also, for each
 $x\in B_{(t,s)}$
, the fibre
$x\in B_{(t,s)}$
, the fibre
 $(\pi _{|C})^{-1}(x)\cap C_{(t,s)}$
is closed and bounded. Let
$(\pi _{|C})^{-1}(x)\cap C_{(t,s)}$
is closed and bounded. Let
 $(x,y)\in C$
be an element in the closure of
$(x,y)\in C$
be an element in the closure of
 $C_{(t,s)}$
. Then
$C_{(t,s)}$
. Then
 $x\in B_{(t,s)}$
and
$x\in B_{(t,s)}$
and
 $(x,y)\in (\pi _{|C})^{-1}(x)\cap C_{(t,s)}\subseteq C_{(t,s)}$
. So
$(x,y)\in (\pi _{|C})^{-1}(x)\cap C_{(t,s)}\subseteq C_{(t,s)}$
. So
 $C_{(t,s)}$
is a closed and bounded subset of C.
$C_{(t,s)}$
is a closed and bounded subset of C.
We observe that from this construction, we obtain:
Claim 6.16. For
![]() $(t,s)$
as above, there is a covering
$(t,s)$
as above, there is a covering
![]() ${\mathcal {U}}_{C} = \{U_i : i \in I\}$
of
${\mathcal {U}}_{C} = \{U_i : i \in I\}$
of
![]() $C \backslash C_{(t,s)}$
by relatively open bounded subsets of C such that:
$C \backslash C_{(t,s)}$
by relatively open bounded subsets of C such that:
-
(1) The index set I is the family of the closed faces of an r-dimensional cube. (So
 $|I| = 2r$
).
$|I| = 2r$
). -
(2) If
 $E \subseteq I,$
then
$E \subseteq I,$
then
 $U_{E} := \bigcap _{i \in E}U_{i}$
is either empty or a
$U_{E} := \bigcap _{i \in E}U_{i}$
is either empty or a
 ${\mathbf {\Gamma }_{\infty } }$
-cell. (So in particular
${\mathbf {\Gamma }_{\infty } }$
-cell. (So in particular
 $H^{p}(U_{E}; L_C) = 0$
for
$H^{p}(U_{E}; L_C) = 0$
for
 $p> 0$
and, if
$p> 0$
and, if
 $U_{E} \neq \emptyset , H^{0}(U_{E}; L_C) = L$
.)
$U_{E} \neq \emptyset , H^{0}(U_{E}; L_C) = L$
.) -
(3) For
 $E \subseteq I, \ U_{E} \neq \emptyset $
iff the faces of the cubes belonging to E have a non-empty intersection.
$E \subseteq I, \ U_{E} \neq \emptyset $
iff the faces of the cubes belonging to E have a non-empty intersection.
So the nerve of
![]() ${\mathcal U}_C$
is isomorphic to the nerve of a covering of an r-cube by its closed faces.
${\mathcal U}_C$
is isomorphic to the nerve of a covering of an r-cube by its closed faces.
Proof. To show that there is a covering satisfying the properties above, we define
![]() ${\mathcal {U}}_C$
by induction on
${\mathcal {U}}_C$
by induction on
![]() $l\in \{1, \ldots , m-1\}$
. We distinguish four cases according to the definition of the
$l\in \{1, \ldots , m-1\}$
. We distinguish four cases according to the definition of the
![]() $C_{(t,s)}$
:
$C_{(t,s)}$
:
-
• If
 $l= 1$
and C is a singleton in
$l= 1$
and C is a singleton in
 ${\Gamma _{\infty } }$
, then
${\Gamma _{\infty } }$
, then
 $\mathcal {U}_{C}=\{C\}$
.
$\mathcal {U}_{C}=\{C\}$
. -
• If
 $l= 1$
and
$l= 1$
and
 $C = (d, e)\subseteq {\Gamma _{\infty } },$
then
$C = (d, e)\subseteq {\Gamma _{\infty } },$
then  $$ \begin{align*} \mathcal{U}_C = \begin{cases} \{(d,d + \gamma (t,s)) ,(e -\gamma (t,s),e)\}\quad \quad \quad \quad \quad \quad \textrm{if}\quad e< \infty\\ \,\, \\ \{(d,d+\gamma (t,s)), ((d+s)-\gamma(t,s),\infty)\} \quad \quad \quad \textrm{otherwise} \end{cases} \end{align*} $$
$$ \begin{align*} \mathcal{U}_C = \begin{cases} \{(d,d + \gamma (t,s)) ,(e -\gamma (t,s),e)\}\quad \quad \quad \quad \quad \quad \textrm{if}\quad e< \infty\\ \,\, \\ \{(d,d+\gamma (t,s)), ((d+s)-\gamma(t,s),\infty)\} \quad \quad \quad \textrm{otherwise} \end{cases} \end{align*} $$
-
• If
 $l> 1$
and
$l> 1$
and
 $C = \Gamma (f)$
, where
$C = \Gamma (f)$
, where
 $B\subseteq [0,\infty ]^{l}$
is
$B\subseteq [0,\infty ]^{l}$
is
 ${\mathbf {\Gamma }_{\infty } }$
-cell. By definition,
${\mathbf {\Gamma }_{\infty } }$
-cell. By definition,
 $C_{(t,s)}=\Gamma (f_{|B_{(t,s)}})$
. By induction, we have a covering
$C_{(t,s)}=\Gamma (f_{|B_{(t,s)}})$
. By induction, we have a covering
 $\mathcal {V}_B$
of
$\mathcal {V}_B$
of
 $B \backslash B_{(t,s)}$
with the stated properties, and we define
$B \backslash B_{(t,s)}$
with the stated properties, and we define
 ${\mathcal {U}}_C$
to be a covering of
${\mathcal {U}}_C$
to be a covering of
 $C \backslash C_{(t,s)}$
induced by the natural homeomorphism between the graph of f and its domain.
$C \backslash C_{(t,s)}$
induced by the natural homeomorphism between the graph of f and its domain. -
• If
 $l> 1$
and
$l> 1$
and
 $C = (f, g)_{B}$
, where
$C = (f, g)_{B}$
, where
 $B\subseteq [0,\infty ]^{l}$
is
$B\subseteq [0,\infty ]^{l}$
is
 ${\mathbf {\Gamma }_{\infty } }$
-cell and
${\mathbf {\Gamma }_{\infty } }$
-cell and
 $f<g$
. By definition, By induction, we have that
$f<g$
. By definition, By induction, we have that $$ \begin{align*} C_{(t,s)} = \begin{cases} [f +\gamma (t,s), g - \gamma (t,s)]_{B_{(t,s)}}\quad \quad \quad \quad \quad \quad \textrm{if}\quad g< \infty\\ \,\, \\ [f+\gamma (t,s), (f+s)-\gamma(t,s)]_{B_{(t,s)}} \quad \quad \quad \,\, \textrm{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} C_{(t,s)} = \begin{cases} [f +\gamma (t,s), g - \gamma (t,s)]_{B_{(t,s)}}\quad \quad \quad \quad \quad \quad \textrm{if}\quad g< \infty\\ \,\, \\ [f+\gamma (t,s), (f+s)-\gamma(t,s)]_{B_{(t,s)}} \quad \quad \quad \,\, \textrm{otherwise.} \end{cases} \end{align*} $$
 $B \backslash B_{(t,s)}$
has a covering
$B \backslash B_{(t,s)}$
has a covering
 ${\mathcal V}_B = \{V_{j} : j \in J\}$
with the stated properties, where J is the set of closed faces of the cube
${\mathcal V}_B = \{V_{j} : j \in J\}$
with the stated properties, where J is the set of closed faces of the cube
 $[0, 1]^{r-1}$
. Define a covering
$[0, 1]^{r-1}$
. Define a covering
 ${\mathcal {U}}_C = \{U_i : i \in I\}$
of
${\mathcal {U}}_C = \{U_i : i \in I\}$
of
 $C \backslash C_{(t,s)}$
as follows. As index set I, we take the closed faces of the cube
$C \backslash C_{(t,s)}$
as follows. As index set I, we take the closed faces of the cube
 $[0, 1]^r$
. Thus
$[0, 1]^r$
. Thus
 $|I|=|J|+2,$
with the two extra faces corresponding to the ‘top’ and ‘bottom’ faces of
$|I|=|J|+2,$
with the two extra faces corresponding to the ‘top’ and ‘bottom’ faces of
 $[0, 1]^r$
. We associate to the top face the open set
$[0, 1]^r$
. We associate to the top face the open set
 $(g - \gamma (t,s), g)_{B}$
if
$(g - \gamma (t,s), g)_{B}$
if
 $g<\infty $
or
$g<\infty $
or
 $((f+s) - \gamma (t,s), \infty )_{B}$
if
$((f+s) - \gamma (t,s), \infty )_{B}$
if
 $g=\infty $
and the bottom face the open set
$g=\infty $
and the bottom face the open set
 $(f, f + \gamma (t,s))_{B}$
. The other open sets of the covering are the preimages of the sets
$(f, f + \gamma (t,s))_{B}$
. The other open sets of the covering are the preimages of the sets
 $V_j$
under the restriction of the projection
$V_j$
under the restriction of the projection
 $\Gamma ^{l+1}_{\infty } \rightarrow {\Gamma ^l_{\infty } }$
. This defines a covering of
$\Gamma ^{l+1}_{\infty } \rightarrow {\Gamma ^l_{\infty } }$
. This defines a covering of
 $C \backslash C_{(t,s)}$
with the stated properties.
$C \backslash C_{(t,s)}$
with the stated properties.
Property (1) of the lemma is clear. By (the proof of) Claim 6.16, there are open covers
![]() ${\mathcal U}^{\prime }_C$
of
${\mathcal U}^{\prime }_C$
of
![]() $C \backslash C_{(t',s')}$
and
$C \backslash C_{(t',s')}$
and
![]() ${\mathcal U}_C$
of
${\mathcal U}_C$
of
![]() $C \backslash C_{(t,s)}$
satisfying the assumptions of [Reference Berarducci and Fornasiero7, Lemma 5.5]. Hence property (2) of the lemma holds. Finally, if
$C \backslash C_{(t,s)}$
satisfying the assumptions of [Reference Berarducci and Fornasiero7, Lemma 5.5]. Hence property (2) of the lemma holds. Finally, if
![]() $r>1$
, then property (3) follows from Claim 6.16 and [Reference Berarducci and Fornasiero7, Corollary 5.2]. On the other hand, if
$r>1$
, then property (3) follows from Claim 6.16 and [Reference Berarducci and Fornasiero7, Corollary 5.2]. On the other hand, if
![]() $r=1$
, then
$r=1$
, then
![]() $C\setminus C_{(t,s)}$
is by construction a disjoint union
$C\setminus C_{(t,s)}$
is by construction a disjoint union
![]() $D\sqcup E$
of two
$D\sqcup E$
of two
![]() ${\mathbf {\Gamma }_{\infty } }$
-cells in
${\mathbf {\Gamma }_{\infty } }$
-cells in
![]() $[0,\infty ]^m$
of dimension
$[0,\infty ]^m$
of dimension
![]() $r=1$
. Therefore, in this case, the result follows from Lemma 6.14, since
$r=1$
. Therefore, in this case, the result follows from Lemma 6.14, since
![]() $H^{*}(C \backslash C_{(t,s)}; L_C) \simeq H^*(D;L_D)\oplus H^*(E;L_E)$
.
$H^{*}(C \backslash C_{(t,s)}; L_C) \simeq H^*(D;L_D)\oplus H^*(E;L_E)$
.
It remains to show property (4). Note that if
![]() $0< t'< t<s<s',$
then by construction,
$0< t'< t<s<s',$
then by construction,
![]() $C_{(t',s')}$
contains the interior relative to C of
$C_{(t',s')}$
contains the interior relative to C of
![]() $C_{(t,s)}$
. Thus C is a directed union
$C_{(t,s)}$
. Thus C is a directed union
![]() $\bigcup _{(t,s)}U_{(t,s)}$
of a
$\bigcup _{(t,s)}U_{(t,s)}$
of a
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable family of relatively open
${\mathbf {\Gamma }_{\infty } }$
-definable family of relatively open
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable subsets. In particular, if
${\mathbf {\Gamma }_{\infty } }$
-definable subsets. In particular, if
![]() $K\subseteq C$
is a
$K\subseteq C$
is a
![]() ${\mathbf {\Gamma }_{\infty } }$
-definably compact subset, then
${\mathbf {\Gamma }_{\infty } }$
-definably compact subset, then
![]() $\{K\cap U_{(t,s)} : 0<t<s\}$
is a
$\{K\cap U_{(t,s)} : 0<t<s\}$
is a
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable family of open
${\mathbf {\Gamma }_{\infty } }$
-definable family of open
![]() ${\mathbf {\Gamma }_{\infty } }$
-definable subsets of K with the property that every finite subset of K is contained in one of the
${\mathbf {\Gamma }_{\infty } }$
-definable subsets of K with the property that every finite subset of K is contained in one of the
![]() $K\cap U_{(t,s)}$
. Therefore, since K is closed and bounded (Remark 4.11), by [Reference Peterzil and Pillay44, Corollary 2.2 (ii)], there are
$K\cap U_{(t,s)}$
. Therefore, since K is closed and bounded (Remark 4.11), by [Reference Peterzil and Pillay44, Corollary 2.2 (ii)], there are
![]() $0<t<s$
such that
$0<t<s$
such that
![]() $K\subseteq U_{(t,s)}\subseteq C_{(t,s)}$
.
$K\subseteq U_{(t,s)}\subseteq C_{(t,s)}$
.
From Lemma 6.15 and computations using excision axiom ([Reference Bredon14, Chapter II, 12.9]) and long exactness sequence ([Reference Bredon14, Chapter II, Section 12 (22)]), we obtain just as in [Reference Berarducci and Fornasiero7, Lemma 7.2]:
Lemma 6.17. Let
![]() $X\subseteq [0,\infty ]^m$
be a definable set and
$X\subseteq [0,\infty ]^m$
be a definable set and
![]() $C\subseteq X$
be a cell of maximal dimension. Then for every
$C\subseteq X$
be a cell of maximal dimension. Then for every
![]() $0<t'<t<\frac {s}{2}<s<s'$
, we have isomorphisms induced by inclusions:
$0<t'<t<\frac {s}{2}<s<s'$
, we have isomorphisms induced by inclusions:
□
The next result is the analogue of [Reference Berarducci and Fornasiero7, Corollary 7.3], but we have to explain how to use [Reference Berarducci and Fornasiero7, Lemma 6.7] in our context:
Lemma 6.18. Let
![]() $X\subseteq [0,\infty ]^m$
be a closed definable set and
$X\subseteq [0,\infty ]^m$
be a closed definable set and
![]() $C\subseteq X$
be a cell of maximal dimension. Then for every
$C\subseteq X$
be a cell of maximal dimension. Then for every
![]() $0<t<s$
, we have isomorphisms induced by inclusions:
$0<t<s$
, we have isomorphisms induced by inclusions:
Proof. Let
![]() $Z=X\setminus C$
, and for
$Z=X\setminus C$
, and for
![]() $0<t<s$
, let
$0<t<s$
, let
![]() $Y_{(t,s)}=X\setminus C_{(t,s)}$
. Let V be an open definable neighbourhood of Z in X. Since
$Y_{(t,s)}=X\setminus C_{(t,s)}$
. Let V be an open definable neighbourhood of Z in X. Since
![]() $K=X\setminus V\subseteq C$
is a definably compact subset, by Lemma 6.15 (4), there are
$K=X\setminus V\subseteq C$
is a definably compact subset, by Lemma 6.15 (4), there are
![]() $0<t<s$
such that
$0<t<s$
such that
![]() $K\subseteq C_{(t,s)}\subseteq C$
. Therefore,
$K\subseteq C_{(t,s)}\subseteq C$
. Therefore,
![]() $Z\subseteq Y_{(t,s)}\subseteq V$
. On the other hand,
$Z\subseteq Y_{(t,s)}\subseteq V$
. On the other hand,
![]() $\widetilde {Y_{(t,s)}}$
for all
$\widetilde {Y_{(t,s)}}$
for all
![]() $0<t<s$
are taut in
$0<t<s$
are taut in
![]() $\widetilde {X}$
, being open subsets ([Reference Bredon14, page 73]); and since X is definably normal (being definably compact) and Z is a closed subset, the family of all closed subsets of
$\widetilde {X}$
, being open subsets ([Reference Bredon14, page 73]); and since X is definably normal (being definably compact) and Z is a closed subset, the family of all closed subsets of
![]() $\widetilde {X}$
is a normal and constructible family of supports on
$\widetilde {X}$
is a normal and constructible family of supports on
![]() $\widetilde {X}$
, so by Corollary 3.28,
$\widetilde {X}$
, so by Corollary 3.28,
![]() $\widetilde {Z}$
is taut in
$\widetilde {Z}$
is taut in
![]() $\widetilde {X}$
. Therefore, by the purely topological [Reference Berarducci and Fornasiero7, Lemma 6.4], together with Lemma 6.17 and [Reference Berarducci and Fornasiero7, Remark 6.6], we have
$\widetilde {X}$
. Therefore, by the purely topological [Reference Berarducci and Fornasiero7, Lemma 6.4], together with Lemma 6.17 and [Reference Berarducci and Fornasiero7, Remark 6.6], we have
Remark 6.19. Let
![]() $X\subseteq {\Gamma ^m_{\infty } }$
be a definably locally closed subset. By Remark 4.13, there is a definably compact subset
$X\subseteq {\Gamma ^m_{\infty } }$
be a definably locally closed subset. By Remark 4.13, there is a definably compact subset
![]() $P\subseteq {\Gamma ^m_{\infty } }$
such that X is an open definable subset of P. Since by Remark 4.14, P is definably normal and every definably compact subset of X is a closed definable subset of P, it follows from Definition 3.11 (2) that the family, which we will denote by c, of all definably compact definable subsets of X is a family of definably normal supports on X.
$P\subseteq {\Gamma ^m_{\infty } }$
such that X is an open definable subset of P. Since by Remark 4.14, P is definably normal and every definably compact subset of X is a closed definable subset of P, it follows from Definition 3.11 (2) that the family, which we will denote by c, of all definably compact definable subsets of X is a family of definably normal supports on X.
Below, we will assume some properties of the corresponding cohomology with definably compact supports; see, for instance, [Reference Edmundo and Prelli27]. In particular, we observe that if
![]() $Z\subseteq X$
is definably compact, then
$Z\subseteq X$
is definably compact, then
![]() $H^*_c(Z;L_Z)\simeq H^*(Z; L_Z)$
.
$H^*_c(Z;L_Z)\simeq H^*(Z; L_Z)$
.
Theorem 6.20. Let A be a noetherian ring, and let L be a finitely generated A-module. If
![]() $X\subseteq {\Gamma ^m_{\infty } }$
is a definably locally closed subset, then
$X\subseteq {\Gamma ^m_{\infty } }$
is a definably locally closed subset, then
![]() $H^p_c(X;L_X)$
is finitely generated for each p. Moreover,
$H^p_c(X;L_X)$
is finitely generated for each p. Moreover,
![]() $H^p_c(X;L_X)=0$
for
$H^p_c(X;L_X)=0$
for
![]() $p>\dim X$
.
$p>\dim X$
.
Proof. Let
![]() $i\colon X\hookrightarrow P\subseteq [0,\infty ]^{2m}$
be a definable completion of X (Remark 4.13). Since P is a closed subset of
$i\colon X\hookrightarrow P\subseteq [0,\infty ]^{2m}$
be a definable completion of X (Remark 4.13). Since P is a closed subset of
![]() $[0,\infty ]^{2m},$
from Lemma 6.18 and computations using Mayer-Vietoris sequence ([Reference Bredon14, Chapter II, Section 13 (32)]; see Remark 6.12), we obtain just as in [Reference Berarducci and Fornasiero7, Theorem 7.4] that
$[0,\infty ]^{2m},$
from Lemma 6.18 and computations using Mayer-Vietoris sequence ([Reference Bredon14, Chapter II, Section 13 (32)]; see Remark 6.12), we obtain just as in [Reference Berarducci and Fornasiero7, Theorem 7.4] that
![]() $H^p(P;L_P)$
is finitely generated for each p and
$H^p(P;L_P)$
is finitely generated for each p and
![]() $H^p(P;L_P)=0$
for
$H^p(P;L_P)=0$
for
![]() $p>\dim P$
. Since X is an open definable subset of
$p>\dim P$
. Since X is an open definable subset of
![]() $P, \ P\setminus X$
is a closed subset of
$P, \ P\setminus X$
is a closed subset of
![]() $[0,\infty ]^{2m}$
, and similarly, we have that
$[0,\infty ]^{2m}$
, and similarly, we have that
![]() $H^p(P\setminus X;L_{P\setminus X})$
is finitely generated for each p and
$H^p(P\setminus X;L_{P\setminus X})$
is finitely generated for each p and
![]() $H^p(P\setminus X;L_{P\setminus X})=0$
for
$H^p(P\setminus X;L_{P\setminus X})=0$
for
![]() $p>\dim P\setminus X$
.
$p>\dim P\setminus X$
.
By Equation (1) on page 5, if
![]() $Z\subseteq P$
is a definably locally closed subset, then we have
$Z\subseteq P$
is a definably locally closed subset, then we have
![]() $L_Z=i_{!}(L_{P\,|Z})$
. Then Corollary 3.27 together with the short exact coefficients sequence
$L_Z=i_{!}(L_{P\,|Z})$
. Then Corollary 3.27 together with the short exact coefficients sequence
yields the long exact cohomology sequence
Since P is the closure of X, we have
![]() $\dim X=\dim P$
and
$\dim X=\dim P$
and
![]() $\dim P\setminus X<\dim P$
([Reference van den Dries53, Chapter 4, (1.8)]). It follows that
$\dim P\setminus X<\dim P$
([Reference van den Dries53, Chapter 4, (1.8)]). It follows that
![]() $H^p_c(X;L_X)=0$
for all
$H^p_c(X;L_X)=0$
for all
![]() $p>\dim X$
. It also follows that
$p>\dim X$
. It also follows that
![]() $\ker \beta =\mathrm {Im}\,\alpha $
is finitely generated and
$\ker \beta =\mathrm {Im}\,\alpha $
is finitely generated and
![]() $\mathrm {Im}\,\beta $
is finitely generated. Thus we see that
$\mathrm {Im}\,\beta $
is finitely generated. Thus we see that
![]() $H^p_c(X;L_X)$
is finitely generated for each p.
$H^p_c(X;L_X)$
is finitely generated for each p.
Below, we will require the following, which is obtained by going to
![]() $\widetilde {{\mathfrak T}}$
and applying the corresponding criterion in the topological case ([Reference Bredon14, Chapter II, 16.12]) (point (iii) is a little stronger here), observing that
$\widetilde {{\mathfrak T}}$
and applying the corresponding criterion in the topological case ([Reference Bredon14, Chapter II, 16.12]) (point (iii) is a little stronger here), observing that
![]() $\widetilde {U}$
with
$\widetilde {U}$
with
![]() $U\in \mathrm {Op}(X_{{\mathcal {T}}})$
forms a filtrant basis for the topology of
$U\in \mathrm {Op}(X_{{\mathcal {T}}})$
forms a filtrant basis for the topology of
![]() $\widetilde {X}_{{\mathcal {T}}}.$
$\widetilde {X}_{{\mathcal {T}}}.$
Lemma 6.21. Let
![]() $(X,{\mathcal {T}})$
be an object of
$(X,{\mathcal {T}})$
be an object of
![]() ${\mathfrak T}$
, and let
${\mathfrak T}$
, and let
![]() $\mathfrak {R}$
be a class of objects of
$\mathfrak {R}$
be a class of objects of
![]() $\mathrm {Mod} (A_{X_{{\mathcal {T}}}}).$
Suppose that
$\mathrm {Mod} (A_{X_{{\mathcal {T}}}}).$
Suppose that
![]() $\mathfrak {R}$
satisfies:
$\mathfrak {R}$
satisfies:
-
(i) For each exact sequence
 $0 \to {{\mathcal {F}}'} \to {{\mathcal {F}}} \to {{\mathcal {F}}"} \to 0$
with
$0 \to {{\mathcal {F}}'} \to {{\mathcal {F}}} \to {{\mathcal {F}}"} \to 0$
with
 ${\mathcal {F}}' \in \mathfrak {R}$
, we have
${\mathcal {F}}' \in \mathfrak {R}$
, we have
 ${\mathcal {F}} \in \mathfrak {R}$
if and only if
${\mathcal {F}} \in \mathfrak {R}$
if and only if
 ${\mathcal {F}}" \in \mathfrak {R}$
.
${\mathcal {F}}" \in \mathfrak {R}$
. -
(ii)
 $\mathfrak {R}$
is stable under filtrant
$\mathfrak {R}$
is stable under filtrant
 $\underrightarrow {\lim }$
.
$\underrightarrow {\lim }$
. -
(iii)
 $A_V \in \mathfrak {R}$
for any
$A_V \in \mathfrak {R}$
for any
 $V \in \mathrm {Op}(X_{{\mathcal {T}}}).$
$V \in \mathrm {Op}(X_{{\mathcal {T}}}).$
Then
![]() $\mathfrak {R}=\mathrm {Mod}(A_{X_{{\mathcal {T}}}})$
.
$\mathfrak {R}=\mathrm {Mod}(A_{X_{{\mathcal {T}}}})$
.
![]() $\Box $
$\Box $
Recall that if
![]() ${\mathbf {\Gamma }} '$
is an elementary extension of
${\mathbf {\Gamma }} '$
is an elementary extension of
![]() ${\mathbf {\Gamma }}$
or an o-minimal expansion of
${\mathbf {\Gamma }}$
or an o-minimal expansion of
![]() ${\mathbf {\Gamma }}$
and
${\mathbf {\Gamma }}$
and
![]() $Y\subseteq {\Gamma ^m_{\infty } }$
is a definable subset, then we have a natural morphism of sites
$Y\subseteq {\Gamma ^m_{\infty } }$
is a definable subset, then we have a natural morphism of sites
If
![]() ${\mathcal {F}} \in \mathrm {Mod}(A_{Y_{\mathrm {def}}})$
, then we have a corresponding
${\mathcal {F}} \in \mathrm {Mod}(A_{Y_{\mathrm {def}}})$
, then we have a corresponding
![]() ${\mathcal {F}}({\mathbf {\Gamma }}' _{\infty })\in \mathrm {Mod} (A_{Y({\mathbf {\Gamma }}^{\prime }_{\infty })_{\mathrm {def}}})$
given by inverse image.
${\mathcal {F}}({\mathbf {\Gamma }}' _{\infty })\in \mathrm {Mod} (A_{Y({\mathbf {\Gamma }}^{\prime }_{\infty })_{\mathrm {def}}})$
given by inverse image.
Theorem 6.22. Let
![]() ${\mathbf {\Gamma }} '$
be an elementary extension of
${\mathbf {\Gamma }} '$
be an elementary extension of
![]() ${\mathbf {\Gamma }}$
or an o-minimal expansion of
${\mathbf {\Gamma }}$
or an o-minimal expansion of
![]() ${\mathbf {\Gamma }}$
. If
${\mathbf {\Gamma }}$
. If
![]() $X\subseteq {\Gamma ^m_{\infty } }$
is a definably locally closed subset, then for every
$X\subseteq {\Gamma ^m_{\infty } }$
is a definably locally closed subset, then for every
![]() ${\mathcal {F}}\in \mathrm {Mod}(A_{X_{\mathrm {def}}})$
, we have an isomorphism
${\mathcal {F}}\in \mathrm {Mod}(A_{X_{\mathrm {def}}})$
, we have an isomorphism
Proof. Let
![]() $i\colon X\hookrightarrow P\subseteq [0,\infty ]^{2m}$
be a definable completion of X (Remark 4.13). Since P is a closed subset of
$i\colon X\hookrightarrow P\subseteq [0,\infty ]^{2m}$
be a definable completion of X (Remark 4.13). Since P is a closed subset of
![]() $[0,\infty ]^{2m},$
for any closed definable subset
$[0,\infty ]^{2m},$
for any closed definable subset
![]() $Z\subseteq P$
, from Lemma 6.18 and computations using Mayer-Vietoris sequence ([Reference Bredon14, Chapter II, Section 13 (32)]; see Remark 6.12), we obtain just as in [Reference Berarducci and Fornasiero7, Theorems 8.1 and 8.3] an isomorphism
$Z\subseteq P$
, from Lemma 6.18 and computations using Mayer-Vietoris sequence ([Reference Bredon14, Chapter II, Section 13 (32)]; see Remark 6.12), we obtain just as in [Reference Berarducci and Fornasiero7, Theorems 8.1 and 8.3] an isomorphism
Since P is definably compact, it is definably normal, so the family of closed definable subsets of P is a family of definably normal supports on P. Also X is an open definable subset of
![]() $P,$
and hence by Corollary 3.27, if
$P,$
and hence by Corollary 3.27, if
![]() ${\mathcal {F}}\in \mathrm {Mod} (A_{X_{\mathrm {def}}})$
, then
${\mathcal {F}}\in \mathrm {Mod} (A_{X_{\mathrm {def}}})$
, then
By invariance of definably compactness (see Remark 4.11) and Corollary 3.27 in
![]() ${\mathbf {\Gamma }} ^{\prime }_{\infty }$
, we also have
${\mathbf {\Gamma }} ^{\prime }_{\infty }$
, we also have
Moreover, by Equation (2) on page 5 applied to the commutative diagram (with tildes omitted)

we get
![]() $(i_{!}{\mathcal {F}})({\mathbf {\Gamma }} ^{\prime }_{\infty })=i^{{\mathbf {\Gamma }} ^{\prime }_{\infty }}_{!}{\mathcal {F}}({\mathbf {\Gamma }} ^{\prime }_{\infty })$
, so
$(i_{!}{\mathcal {F}})({\mathbf {\Gamma }} ^{\prime }_{\infty })=i^{{\mathbf {\Gamma }} ^{\prime }_{\infty }}_{!}{\mathcal {F}}({\mathbf {\Gamma }} ^{\prime }_{\infty })$
, so
The result will follow once we show that, for every
![]() ${\mathcal {G}}\in \mathrm {Mod}(A_{P_{\mathrm {def}}})$
, we have an isomorphism
${\mathcal {G}}\in \mathrm {Mod}(A_{P_{\mathrm {def}}})$
, we have an isomorphism
But this is obtained by applying Lemma 6.21 in the following way. For (i), the exact sequence
![]() $0 \to {\mathcal {F}}' \to {\mathcal {F}} \to {\mathcal {F}}" \to 0$
implies the following chain of morphisms in cohomology (
$0 \to {\mathcal {F}}' \to {\mathcal {F}} \to {\mathcal {F}}" \to 0$
implies the following chain of morphisms in cohomology (
![]() $j \in \mathbb {Z}$
):
$j \in \mathbb {Z}$
):

Therefore, if we have isomorphisms for
![]() ${\mathcal {F}}',$
then using the five lemmas, we have isomorphisms for
${\mathcal {F}}',$
then using the five lemmas, we have isomorphisms for
![]() ${\mathcal {F}}$
if and only if we have isomorphisms for
${\mathcal {F}}$
if and only if we have isomorphisms for
![]() ${\mathcal {F}}" $
.
${\mathcal {F}}" $
.
For (ii), first note that (a) sections commute with filtrant
![]() $\underrightarrow {\lim }$
([Reference Edmundo and Prelli27, Example 1.1.4 and Proposition 1.2.12]); (b) filtrant
$\underrightarrow {\lim }$
([Reference Edmundo and Prelli27, Example 1.1.4 and Proposition 1.2.12]); (b) filtrant
![]() $\underrightarrow {\lim }$
of
$\underrightarrow {\lim }$
of
![]() ${\mathcal {T}}$
-flabby sheaves is
${\mathcal {T}}$
-flabby sheaves is
![]() ${\mathcal {T}}$
-flabby ([Reference Edmundo and Prelli27, Proposition 2.3.4 (i)]); (c) the full additive subcategory of
${\mathcal {T}}$
-flabby ([Reference Edmundo and Prelli27, Proposition 2.3.4 (i)]); (c) the full additive subcategory of
![]() ${\mathcal {T}}$
-flabby objects is
${\mathcal {T}}$
-flabby objects is
![]() $\Gamma (U;\bullet )$
-injective for every
$\Gamma (U;\bullet )$
-injective for every
![]() $U\in \mathrm {Op}(P_{{\mathcal {T}}})$
([Reference Edmundo and Prelli27, Proposition 2.3.5]). This implies that
$U\in \mathrm {Op}(P_{{\mathcal {T}}})$
([Reference Edmundo and Prelli27, Proposition 2.3.5]). This implies that
![]() $H^*(P;\underrightarrow {\lim } {\mathcal {F}}_i)=\underrightarrow {\lim } H^*(P;{\mathcal {F}}_i).$
Since the same facts hold in
$H^*(P;\underrightarrow {\lim } {\mathcal {F}}_i)=\underrightarrow {\lim } H^*(P;{\mathcal {F}}_i).$
Since the same facts hold in
![]() ${\mathbf {\Gamma }} ^{\prime }_{\infty }$
, we have
${\mathbf {\Gamma }} ^{\prime }_{\infty }$
, we have
![]() $H^*(P({\mathbf {\Gamma }} ^{\prime }_{\infty });\underrightarrow {\lim } ({\mathcal {F}}_i({\mathbf {\Gamma }} ^{\prime }_{\infty })))=\underrightarrow {\lim } H^*(P({\mathbf {\Gamma }} ^{\prime }_{\infty });{\mathcal {F}}_i({\mathbf {\Gamma }} ^{\prime }_{\infty }))$
, and (ii) follows since
$H^*(P({\mathbf {\Gamma }} ^{\prime }_{\infty });\underrightarrow {\lim } ({\mathcal {F}}_i({\mathbf {\Gamma }} ^{\prime }_{\infty })))=\underrightarrow {\lim } H^*(P({\mathbf {\Gamma }} ^{\prime }_{\infty });{\mathcal {F}}_i({\mathbf {\Gamma }} ^{\prime }_{\infty }))$
, and (ii) follows since
![]() $\underrightarrow {\lim } ({\mathcal {F}}_i({\mathbf {\Gamma }} ^{\prime }_{\infty }))=(\underrightarrow {\lim } {\mathcal {F}}_i)({\mathbf {\Gamma }} ^{\prime }_{\infty })$
(inverse image commutes with
$\underrightarrow {\lim } ({\mathcal {F}}_i({\mathbf {\Gamma }} ^{\prime }_{\infty }))=(\underrightarrow {\lim } {\mathcal {F}}_i)({\mathbf {\Gamma }} ^{\prime }_{\infty })$
(inverse image commutes with
![]() $\underrightarrow {\lim }$
).
$\underrightarrow {\lim }$
).
For (iii), if
![]() $V\in \mathrm {Op}(P_{{\mathcal {T}}})$
, then the exact sequence
$V\in \mathrm {Op}(P_{{\mathcal {T}}})$
, then the exact sequence
![]() $0 \to A_V \to A_P \to A_{P\setminus V} \to 0$
implies the following chain of morphisms in cohomology (
$0 \to A_V \to A_P \to A_{P\setminus V} \to 0$
implies the following chain of morphisms in cohomology (
![]() $j \in \mathbb {Z}$
)
$j \in \mathbb {Z}$
)

where we are using that
![]() $P({\mathbf {\Gamma }} ^{\prime }_{\infty })\setminus V({\mathbf {\Gamma }} ^{\prime }_{\infty })=(P\setminus V)({\mathbf {\Gamma }} ^{\prime }_{\infty })$
. Since
$P({\mathbf {\Gamma }} ^{\prime }_{\infty })\setminus V({\mathbf {\Gamma }} ^{\prime }_{\infty })=(P\setminus V)({\mathbf {\Gamma }} ^{\prime }_{\infty })$
. Since
![]() $P\setminus V$
is a closed definable subset of P, we have as observed above
$P\setminus V$
is a closed definable subset of P, we have as observed above
![]() $H^*(P\setminus V; A_{P\setminus V})\simeq H^*((P\setminus V)({\mathbf {\Gamma }} ^{\prime }_{\infty }); A_{(P\setminus V)({\mathbf {\Gamma }} ^{\prime }_{\infty })})$
. But by Corollary 3.27
$H^*(P\setminus V; A_{P\setminus V})\simeq H^*((P\setminus V)({\mathbf {\Gamma }} ^{\prime }_{\infty }); A_{(P\setminus V)({\mathbf {\Gamma }} ^{\prime }_{\infty })})$
. But by Corollary 3.27
![]() $H^*(P; A_{P\setminus V})\simeq H^*(P\setminus V; A_{P\setminus V})$
and by the same result in
$H^*(P; A_{P\setminus V})\simeq H^*(P\setminus V; A_{P\setminus V})$
and by the same result in
![]() ${\mathbf {\Gamma }} ^{\prime }_{\infty }$
, we have
${\mathbf {\Gamma }} ^{\prime }_{\infty }$
, we have
![]() $H^*(P({\mathbf {\Gamma }} ^{\prime }_{\infty }); A_{(P\setminus V)({\mathbf {\Gamma }} ^{\prime }_{\infty })})\simeq H^*((P\setminus V)({\mathbf {\Gamma }} ^{\prime }_{\infty }); A_{(P\setminus V)({\mathbf {\Gamma }} ^{\prime }_{\infty })})$
. So (iii) follows now using the five lemmas.
$H^*(P({\mathbf {\Gamma }} ^{\prime }_{\infty }); A_{(P\setminus V)({\mathbf {\Gamma }} ^{\prime }_{\infty })})\simeq H^*((P\setminus V)({\mathbf {\Gamma }} ^{\prime }_{\infty }); A_{(P\setminus V)({\mathbf {\Gamma }} ^{\prime }_{\infty })})$
. So (iii) follows now using the five lemmas.
Remark 6.23. In the paper [Reference Edmundo and Prelli26], it was shown that in an arbitrary o-minimal structure
![]() ${\mathbf M}$
with definable Skolem functions, on full subcategories
${\mathbf M}$
with definable Skolem functions, on full subcategories
![]() $\widetilde {{\mathbf A}}$
of
$\widetilde {{\mathbf A}}$
of
![]() $\widetilde {\mathrm {Def}}$
, the category of o-minimal spectra of definable spaces equipped with the o-minimal site satisfying the following properties, one can develop the formalism of the six Grothendieck operations:
$\widetilde {\mathrm {Def}}$
, the category of o-minimal spectra of definable spaces equipped with the o-minimal site satisfying the following properties, one can develop the formalism of the six Grothendieck operations:
-
(A0) Cartesian products (in
 $\widetilde {\mathrm {Def}}$
) of objects of
$\widetilde {\mathrm {Def}}$
) of objects of
 $\widetilde {{\mathbf A}}$
are objects of
$\widetilde {{\mathbf A}}$
are objects of
 $\widetilde {{\mathbf A}}$
, and locally closed constructible subsets of objects of
$\widetilde {{\mathbf A}}$
, and locally closed constructible subsets of objects of
 $\widetilde {{\mathbf A}}$
are objects of
$\widetilde {{\mathbf A}}$
are objects of
 $\widetilde {{\mathbf A}};$
$\widetilde {{\mathbf A}};$
-
(A1) In every object of
 $\widetilde {{\mathbf A}}$
, every open constructible subset is a finite union of open and normal constructible subsets;
$\widetilde {{\mathbf A}}$
, every open constructible subset is a finite union of open and normal constructible subsets; -
(A2) Every object of
 $\widetilde {{\mathbf A}}$
has a completion in
$\widetilde {{\mathbf A}}$
has a completion in
 $\widetilde {{\mathbf A}}.$
$\widetilde {{\mathbf A}}.$
For some of the results about the proper direct image (base change formula, derived base change formula, the Künneth formula and dual base change formula), we required that the morphisms
![]() $\widetilde {f}:\widetilde {X}\to \widetilde {Y}$
in
$\widetilde {f}:\widetilde {X}\to \widetilde {Y}$
in
![]() $\widetilde {{\mathbf A}}$
involved satisfy the following:
$\widetilde {{\mathbf A}}$
involved satisfy the following:
-
(A3) If
 $u\in Y$
, then for every elementary extension
$u\in Y$
, then for every elementary extension
 ${\mathbf S}$
of
${\mathbf S}$
of
 ${\mathbf M}$
and every
${\mathbf M}$
and every
 $F\in \mathrm {Mod} (A_{X_{\mathrm {def}}})$
, we have an isomorphism of cohomology with definably compact supports, where
$F\in \mathrm {Mod} (A_{X_{\mathrm {def}}})$
, we have an isomorphism of cohomology with definably compact supports, where $$ \begin{align*} H^*_c(f^{-1}(u); F_{|f^{-1}(u)})\simeq H^*_c((f^{{\mathbf S}})^{-1}(u); F({\mathbf S})_{|(f^{{\mathbf S}})^{-1}(u)}) \end{align*} $$
$$ \begin{align*} H^*_c(f^{-1}(u); F_{|f^{-1}(u)})\simeq H^*_c((f^{{\mathbf S}})^{-1}(u); F({\mathbf S})_{|(f^{{\mathbf S}})^{-1}(u)}) \end{align*} $$
 $\widetilde {F}({\mathbf S})=r^{-1}\widetilde {F}$
and
$\widetilde {F}({\mathbf S})=r^{-1}\widetilde {F}$
and
 $r:\widetilde {X({\mathbf S})}\to \widetilde {X}$
is the canonical restriction.
$r:\widetilde {X({\mathbf S})}\to \widetilde {X}$
is the canonical restriction.
The work done here gives a new example where we have this formalism: namely, for the category of definably locally closed definable sets in
![]() ${\mathbf {\Gamma }_{\infty } }$
. Of course, in this case, (A0) is obvious. For (A1), (A2) and (A3), see, respectively, Corollary 5.31, Remark 4.13 and Theorem 6.22.
${\mathbf {\Gamma }_{\infty } }$
. Of course, in this case, (A0) is obvious. For (A1), (A2) and (A3), see, respectively, Corollary 5.31, Remark 4.13 and Theorem 6.22.
6.3 Finiteness and invariance results in ACVF and stable completions
Here we will use the finiteness and invariance results for o-minimal cohomology with definably compact supports of definably locally closed subsets of
![]() ${\Gamma ^m_{\infty } }$
and Hrushovski and Loeser’s main theorem ([Reference Hrushovski and Loeser35, Theorem 11.1.1]) to deduce finiteness and invariance results for cohomology in ACVF and in stable completions.
${\Gamma ^m_{\infty } }$
and Hrushovski and Loeser’s main theorem ([Reference Hrushovski and Loeser35, Theorem 11.1.1]) to deduce finiteness and invariance results for cohomology in ACVF and in stable completions.
First we recall a few things. Let V and W be algebraic varieties, a model of ACVF. Let
![]() $Y\subseteq V\times {\Gamma ^m_{\infty } }$
and
$Y\subseteq V\times {\Gamma ^m_{\infty } }$
and
![]() $Z\subseteq W\times {\Gamma ^n_{\infty } }$
be definable subsets. Then:
$Z\subseteq W\times {\Gamma ^n_{\infty } }$
be definable subsets. Then:
-
(1) A pro-definable map
 $g\colon Y\to \widehat {Z}$
is
$g\colon Y\to \widehat {Z}$
is
 $\mathrm {v\!+\!g}$
-continuous if and only if the pullback of an open definable subset of
$\mathrm {v\!+\!g}$
-continuous if and only if the pullback of an open definable subset of
 $\widehat {Z}$
is a
$\widehat {Z}$
is a
 $\mathrm {v\!+\!g}$
-open subset of Y (see page 48 in [Reference Hrushovski and Loeser35]). Since open definable subsets of
$\mathrm {v\!+\!g}$
-open subset of Y (see page 48 in [Reference Hrushovski and Loeser35]). Since open definable subsets of
 $\widehat {Z}$
are exactly the
$\widehat {Z}$
are exactly the
 $\widehat {\mathrm {v\!+\!g}}$
-open subsets of
$\widehat {\mathrm {v\!+\!g}}$
-open subsets of
 $\widehat {Z},$
in our terminology,
$\widehat {Z},$
in our terminology,
 $g\colon Y\to \widehat {Z}$
is
$g\colon Y\to \widehat {Z}$
is
 $\mathrm {v\!+\!g}$
-continuous if and only if g is a morphism
$\mathrm {v\!+\!g}$
-continuous if and only if g is a morphism
 $g\colon Y_{\mathrm {v\!+\!g}} \to \widehat {Z}_{\widehat {\mathrm {v\!+\!g}}}$
of sites.
$g\colon Y_{\mathrm {v\!+\!g}} \to \widehat {Z}_{\widehat {\mathrm {v\!+\!g}}}$
of sites. -
(2) A pro-definable map
 $g\colon Y\to \widehat {W}$
is g-continuous (respectively, v-continuous) if and only if for any regular function
$g\colon Y\to \widehat {W}$
is g-continuous (respectively, v-continuous) if and only if for any regular function
 $h\in {\mathcal {O}}_W(W)$
, the pullback under
$h\in {\mathcal {O}}_W(W)$
, the pullback under
 $\widehat {(\mathrm {val} \circ h)}\circ g $
of a g-open (respectively, v-open) subset of
$\widehat {(\mathrm {val} \circ h)}\circ g $
of a g-open (respectively, v-open) subset of
 ${\Gamma _{\infty } }$
is g-open (respectively, v-open) subset of Y, where a subset of
${\Gamma _{\infty } }$
is g-open (respectively, v-open) subset of Y, where a subset of
 ${\Gamma ^m_{\infty } }$
is g-open (respectively, v-open) if its pullback under
${\Gamma ^m_{\infty } }$
is g-open (respectively, v-open) if its pullback under
 $\mathrm {val} \colon \mathbb {A} ^m\to {\Gamma ^m_{\infty } }$
is g-open (respectively, v-open). It follows that if
$\mathrm {val} \colon \mathbb {A} ^m\to {\Gamma ^m_{\infty } }$
is g-open (respectively, v-open). It follows that if
 $g\colon Y\to \widehat {W}$
is both g-continuous and v-continuous, then g is
$g\colon Y\to \widehat {W}$
is both g-continuous and v-continuous, then g is
 $\mathrm {v\!+\!g}$
-continuous.
$\mathrm {v\!+\!g}$
-continuous. -
(3) Any pro-definable map
 $g\colon Y\to \widehat {Z}$
has a canonical extension
$g\colon Y\to \widehat {Z}$
has a canonical extension
 $G\colon \widehat {Y}\to \widehat {Z}$
that is a pro-definable map ([Reference Hrushovski and Loeser35, Lemma 3.8.1]). G is given by: if
$G\colon \widehat {Y}\to \widehat {Z}$
that is a pro-definable map ([Reference Hrushovski and Loeser35, Lemma 3.8.1]). G is given by: if
 $p\in \widehat {Y}$
and
$p\in \widehat {Y}$
and
 $p=\mathrm {tp}(c/\mathbb {U}),$
then
$p=\mathrm {tp}(c/\mathbb {U}),$
then
 $G(p)\in \widehat {Z}$
is such that
$G(p)\in \widehat {Z}$
is such that
 $G(p)|\mathbb {U}(c)=\mathrm {tp}(d/\mathbb {U})$
with d a realisation of
$G(p)|\mathbb {U}(c)=\mathrm {tp}(d/\mathbb {U})$
with d a realisation of
 $\mathrm {tp}(g(c)/\mathbb {U}(c))$
. It follows that if
$\mathrm {tp}(g(c)/\mathbb {U}(c))$
. It follows that if
 $g\colon Y\to \widehat {Z}$
is
$g\colon Y\to \widehat {Z}$
is
 $\mathrm {v\!+\!g}$
-continuous and U is a
$\mathrm {v\!+\!g}$
-continuous and U is a
 $\mathrm {v\!+\!g}$
-open subset of Z, then
$\mathrm {v\!+\!g}$
-open subset of Z, then
 $\widehat {g^{-1}(\widehat {U})})=G^{-1}(\widehat {U})$
, and the canonical extension G is a morphism of
$\widehat {g^{-1}(\widehat {U})})=G^{-1}(\widehat {U})$
, and the canonical extension G is a morphism of
 $\widehat {\mathrm {v\!+\!g}}$
-sites.
$\widehat {\mathrm {v\!+\!g}}$
-sites.
Let V be a quasi-projective variety. Let
![]() $X\subseteq V\times {\Gamma ^m_{\infty } }$
be a definable subset. By [Reference Hrushovski and Loeser35, Theorem 11.1.1] (see Fact 5.14), let
$X\subseteq V\times {\Gamma ^m_{\infty } }$
be a definable subset. By [Reference Hrushovski and Loeser35, Theorem 11.1.1] (see Fact 5.14), let
![]() $H\colon I\times \widehat {X}\to \widehat {X}$
be the continuous pro-definable deformation retraction with image an iso-definable subset
$H\colon I\times \widehat {X}\to \widehat {X}$
be the continuous pro-definable deformation retraction with image an iso-definable subset
![]() ${\mathfrak X} $
of
${\mathfrak X} $
of
![]() $\widehat {X}$
definably homeomorphic to a definable subset of some
$\widehat {X}$
definably homeomorphic to a definable subset of some
![]() ${\Gamma ^k_{\infty } }$
. Let
${\Gamma ^k_{\infty } }$
. Let
![]() $h\colon {\mathfrak X}\to \mathcal {X}$
be a pro-definable homeomorphism of
$h\colon {\mathfrak X}\to \mathcal {X}$
be a pro-definable homeomorphism of
![]() ${\mathfrak X}$
with a definable subset of
${\mathfrak X}$
with a definable subset of
![]() ${\Gamma ^k_{\infty } }$
.
${\Gamma ^k_{\infty } }$
.
We now make a couple of observations required below that are not explicitly stated in [Reference Hrushovski and Loeser35].
Lemma 6.24. The continuous pro-definable deformation retraction
![]() $H\colon I\times \widehat {X}\to \widehat {X}$
is a morphism of
$H\colon I\times \widehat {X}\to \widehat {X}$
is a morphism of
![]() $\widehat {\mathrm {v\!+\!g}}$
-sites.
$\widehat {\mathrm {v\!+\!g}}$
-sites.
Proof. The statement of [Reference Hrushovski and Loeser35, Theorem 11.1.1] is more general: the deformation retraction respects finitely many definable maps
![]() $\zeta _i\colon X\to {\Gamma _{\infty } }$
with canonical extension
$\zeta _i\colon X\to {\Gamma _{\infty } }$
with canonical extension
![]() $\zeta _i\colon \widehat {X}\to {\Gamma _{\infty } }$
and respects the action of a finite algebraic group acting on V, leaving X globally invariant. For this reason, one can make several reductions such as assuming that
$\zeta _i\colon \widehat {X}\to {\Gamma _{\infty } }$
and respects the action of a finite algebraic group acting on V, leaving X globally invariant. For this reason, one can make several reductions such as assuming that
![]() $m=0$
;
$m=0$
;
![]() $X=V$
and V is a projective and equidimensional variety. Then the proof proceeds by induction on
$X=V$
and V is a projective and equidimensional variety. Then the proof proceeds by induction on
![]() $\dim (V)$
. The case
$\dim (V)$
. The case
![]() $\dim (V)=0$
being trivial, for the case
$\dim (V)=0$
being trivial, for the case
![]() $\dim (V)>0$
, several preliminary reductions are performed, allowing one to essentially reduce the proof to the case of curve fibration. In the end, the homotopy H is the concatenation
$\dim (V)>0$
, several preliminary reductions are performed, allowing one to essentially reduce the proof to the case of curve fibration. In the end, the homotopy H is the concatenation
![]() $H_{\Gamma }^{\alpha }\circ ((H_{\widetilde {base}}\circ H_{curves})\circ H_{inf})$
of the relative curve homotopy
$H_{\Gamma }^{\alpha }\circ ((H_{\widetilde {base}}\circ H_{curves})\circ H_{inf})$
of the relative curve homotopy
![]() $H_{curves}$
, the liftable base homotopy
$H_{curves}$
, the liftable base homotopy
![]() $H_{\widetilde {base}}$
, the purely combinatorial tropical homotopy
$H_{\widetilde {base}}$
, the purely combinatorial tropical homotopy
![]() $H_{{\Gamma }}^{\alpha }$
and the inflation homotopy
$H_{{\Gamma }}^{\alpha }$
and the inflation homotopy
![]() $H_{inf}$
.
$H_{inf}$
.
Furthermore, we have:
-
(i) The inflation homotopy
 $H_{inf}\colon [0,\infty ]\times \widehat {V}\to \widehat {V}$
is given by where D is a closed subvariety of V,
$H_{inf}\colon [0,\infty ]\times \widehat {V}\to \widehat {V}$
is given by where D is a closed subvariety of V, $$ \begin{align*} H_{inf}(t,x)= \begin{cases} F(t,x) & x\in \widehat{V\setminus D}\\ x & x\in \widehat{D} \end{cases} \end{align*} $$
$$ \begin{align*} H_{inf}(t,x)= \begin{cases} F(t,x) & x\in \widehat{V\setminus D}\\ x & x\in \widehat{D} \end{cases} \end{align*} $$
 $F\colon [0,\infty ]\times \widehat {V\setminus D}\to \widehat {V\setminus D}$
is the canonical extension of a
$F\colon [0,\infty ]\times \widehat {V\setminus D}\to \widehat {V\setminus D}$
is the canonical extension of a
 $\mathrm {v\!+\!g}$
-continuous pro-definable map
$\mathrm {v\!+\!g}$
-continuous pro-definable map
 $f\colon [0,\infty ]\times V\setminus D\to \widehat {V\setminus D}$
.
$f\colon [0,\infty ]\times V\setminus D\to \widehat {V\setminus D}$
.
Let
 $U\subseteq V$
be a
$U\subseteq V$
be a
 $\mathrm {v\!+\!g}$
-open subset. Then
$\mathrm {v\!+\!g}$
-open subset. Then
 $U\setminus D$
is a
$U\setminus D$
is a
 $\mathrm {v\!+\!g}$
-open subset of
$\mathrm {v\!+\!g}$
-open subset of
 $V\setminus D$
. Also and so
$V\setminus D$
. Also and so $$ \begin{align*} H_{inf}^{-1}(\widehat{U}\setminus \widehat{D})&= H_{inf}^{-1}(\widehat{U\setminus D})\\ &= F^{-1}(\widehat{U\setminus D})\\ &= \widehat{f^{-1}(\widehat{U\setminus D})} \end{align*} $$
$$ \begin{align*} H_{inf}^{-1}(\widehat{U}\setminus \widehat{D})&= H_{inf}^{-1}(\widehat{U\setminus D})\\ &= F^{-1}(\widehat{U\setminus D})\\ &= \widehat{f^{-1}(\widehat{U\setminus D})} \end{align*} $$
 $H_{inf} ^{-1}(\widehat {U}\setminus \widehat {D})$
is a
$H_{inf} ^{-1}(\widehat {U}\setminus \widehat {D})$
is a
 $\widehat {\mathrm {v\!+\!g}}$
-open subset of
$\widehat {\mathrm {v\!+\!g}}$
-open subset of
 $[0,\infty ]\times \widehat {V\setminus D}$
. It follows that
$[0,\infty ]\times \widehat {V\setminus D}$
. It follows that
 $H_{inf}^{-1}(\widehat {U})=H_{inf} ^{-1} (\widehat {U}\setminus \widehat {D})\cup ([0,\infty ]\times (\widehat {U\cap D}))$
is a
$H_{inf}^{-1}(\widehat {U})=H_{inf} ^{-1} (\widehat {U}\setminus \widehat {D})\cup ([0,\infty ]\times (\widehat {U\cap D}))$
is a
 $\widehat {\mathrm {v\!+\!g}}$
-subset of
$\widehat {\mathrm {v\!+\!g}}$
-subset of
 $[0,\infty ]\times \widehat {V}$
. By [Reference Hrushovski and Loeser35, Lemma 10.3.2],
$[0,\infty ]\times \widehat {V}$
. By [Reference Hrushovski and Loeser35, Lemma 10.3.2],
 $H_{inf}$
is continuous, so
$H_{inf}$
is continuous, so
 $H_{inf}^{-1}(\widehat {U})$
is an open subset of
$H_{inf}^{-1}(\widehat {U})$
is an open subset of
 $[0,\infty ]\times \widehat {V}$
. Therefore, by Fact 5.11,
$[0,\infty ]\times \widehat {V}$
. Therefore, by Fact 5.11,
 $H_{inf}^{-1}(\widehat {U})$
is
$H_{inf}^{-1}(\widehat {U})$
is
 $\widehat {\mathrm {v\!+\!g}}$
-open subset. Hence
$\widehat {\mathrm {v\!+\!g}}$
-open subset. Hence
 $H_{inf}$
is a morphism of
$H_{inf}$
is a morphism of
 $\widehat {\mathrm {v\!+\!g}}$
-sites.
$\widehat {\mathrm {v\!+\!g}}$
-sites.
-
(ii) The relative curve homotopy
 $H_{curve}\colon [0,\infty ]\times \widehat {V_0\cup D_0}\to \widehat {V_0\cup D_0}$
is the canonical extension of a g-continuous and v-continuous homotopy
$H_{curve}\colon [0,\infty ]\times \widehat {V_0\cup D_0}\to \widehat {V_0\cup D_0}$
is the canonical extension of a g-continuous and v-continuous homotopy
 $h_{curves}\colon [0,\infty ]\times V_0\cup D_0\to \widehat {V_0\cup D_0}$
. Hence by the remarks made above,
$h_{curves}\colon [0,\infty ]\times V_0\cup D_0\to \widehat {V_0\cup D_0}$
. Hence by the remarks made above,
 $H_{curves}$
is a morphism of
$H_{curves}$
is a morphism of
 $\widehat {\mathrm {v\!+\!g}}$
-sites.
$\widehat {\mathrm {v\!+\!g}}$
-sites. -
(iii) The base homotopy
 $H_{\widetilde {base}}$
is obtained from the canonical extension of a homotopy
$H_{\widetilde {base}}$
is obtained from the canonical extension of a homotopy
 $h_{base}\colon I\times U\to \widehat {U}$
that is obtained by the induction procedure. Hence, by induction,
$h_{base}\colon I\times U\to \widehat {U}$
that is obtained by the induction procedure. Hence, by induction,
 $H_{\widetilde {base}}$
is also a morphism. By the remarks made above,
$H_{\widetilde {base}}$
is also a morphism. By the remarks made above,
 $H_{curves}$
is a morphism of
$H_{curves}$
is a morphism of
 $\widehat {\mathrm {v\!+\!g}}$
-sites.
$\widehat {\mathrm {v\!+\!g}}$
-sites. -
(iv) The tropical homotopy
 $H_{{\Gamma }}^{\alpha }$
is constructed in the
$H_{{\Gamma }}^{\alpha }$
is constructed in the
 ${\Gamma _{\infty } }$
setting where
${\Gamma _{\infty } }$
setting where
 $\mathrm {v\!+\!g}$
-continuous is the same as definable and continuous, so this homotopy is a also a morphism of
$\mathrm {v\!+\!g}$
-continuous is the same as definable and continuous, so this homotopy is a also a morphism of
 $\widehat {\mathrm {v\!+\!g}}$
-sites.
$\widehat {\mathrm {v\!+\!g}}$
-sites.
We can therefore conclude that H is a morphism of
![]() $\widehat {\mathrm {v\!+\!g}}$
-sites as required.
$\widehat {\mathrm {v\!+\!g}}$
-sites as required.
Lemma 6.25. The pro-definable homeomorphism
![]() $h\colon {\mathfrak X}\to \mathcal {X}$
of
$h\colon {\mathfrak X}\to \mathcal {X}$
of
![]() ${\mathfrak X}$
with a definable subset of
${\mathfrak X}$
with a definable subset of
![]() ${\Gamma ^k_{\infty } }$
is a morphism of
${\Gamma ^k_{\infty } }$
is a morphism of
![]() $\widehat {\mathrm {v\!+\!g}}$
-sites.
$\widehat {\mathrm {v\!+\!g}}$
-sites.
Proof. Let U be a
![]() $\mathrm {v\!+\!g}$
-open subset of X. Then
$\mathrm {v\!+\!g}$
-open subset of X. Then
![]() $\widehat {U}$
is a relatively definable subset of
$\widehat {U}$
is a relatively definable subset of
![]() $\widehat {X}$
. So, since
$\widehat {X}$
. So, since
![]() ${\mathfrak X}$
is an iso-definable subset,
${\mathfrak X}$
is an iso-definable subset,
![]() $ \widehat {U}\cap {\mathfrak X}$
is a relatively definable subset of
$ \widehat {U}\cap {\mathfrak X}$
is a relatively definable subset of
![]() ${\mathfrak X}$
(Lemma 5.16 (c)). By Lemma 5.17,
${\mathfrak X}$
(Lemma 5.16 (c)). By Lemma 5.17,
![]() $(h^{-1})^{-1}(\widehat {U})$
is a relatively definable subset of
$(h^{-1})^{-1}(\widehat {U})$
is a relatively definable subset of
![]() ${\mathcal X}$
, and hence it is an open definable subset and so a
${\mathcal X}$
, and hence it is an open definable subset and so a
![]() $\widehat {\mathrm {v\!+\!g}}$
-open subset (Facts 5.11 and 5.10). Since
$\widehat {\mathrm {v\!+\!g}}$
-open subset (Facts 5.11 and 5.10). Since
![]() $h^{-1}:{\mathcal X}\to {\mathfrak X}$
is a morphism of
$h^{-1}:{\mathcal X}\to {\mathfrak X}$
is a morphism of
![]() $\widehat {\mathrm {v\!+\!g}}$
-sites, so is
$\widehat {\mathrm {v\!+\!g}}$
-sites, so is
![]() $h.$
$h.$
Lemma 6.26. If
![]() $X\subseteq V\times {\Gamma ^m_{\infty } }$
is a
$X\subseteq V\times {\Gamma ^m_{\infty } }$
is a
![]() $\mathrm {v\!+\!g}$
-locally closed subset, then there is a bounded
$\mathrm {v\!+\!g}$
-locally closed subset, then there is a bounded
![]() $\mathrm {v\!+\!g}$
-closed subset
$\mathrm {v\!+\!g}$
-closed subset
![]() $P\subseteq V'\times {\Gamma ^m_{\infty } }$
(for
$P\subseteq V'\times {\Gamma ^m_{\infty } }$
(for
![]() $V'$
a projective variety in which V is open) such that
$V'$
a projective variety in which V is open) such that
![]() $X\subseteq P$
and X is
$X\subseteq P$
and X is
![]() $\mathrm {v\!+\!g}$
-open in P. In addition, if K is an elementary substructure of
$\mathrm {v\!+\!g}$
-open in P. In addition, if K is an elementary substructure of
![]() $\mathbb {U}$
, V is over K and X is K-definable, then P is also K-definable.
$\mathbb {U}$
, V is over K and X is K-definable, then P is also K-definable.
Proof. Indeed, let
![]() $V'$
be a projective variety such that V is an open subset of
$V'$
be a projective variety such that V is an open subset of
![]() $V'$
. Then X is still a
$V'$
. Then X is still a
![]() $\mathrm {v\!+\!g}$
-locally closed subset of
$\mathrm {v\!+\!g}$
-locally closed subset of
![]() $V'\times {\Gamma ^m_{\infty } }$
. Consider the natural definable map
$V'\times {\Gamma ^m_{\infty } }$
. Consider the natural definable map
![]() $l\colon V'\times {\Gamma ^m_{\infty } } \to V'\times [0,\infty ]^{2m}$
, which is
$l\colon V'\times {\Gamma ^m_{\infty } } \to V'\times [0,\infty ]^{2m}$
, which is
![]() $\mathrm {id} _{V'}$
on the first coordinate and on the second coordinate is given as in Remark 4.13. Then
$\mathrm {id} _{V'}$
on the first coordinate and on the second coordinate is given as in Remark 4.13. Then
![]() $l\colon V'\times {\Gamma ^m_{\infty } }\to l(V'\times {\Gamma ^m_{\infty } })\subseteq V'\times [0,\infty ]^{2m}$
is a definable homeomorphism, a morphism of
$l\colon V'\times {\Gamma ^m_{\infty } }\to l(V'\times {\Gamma ^m_{\infty } })\subseteq V'\times [0,\infty ]^{2m}$
is a definable homeomorphism, a morphism of
![]() $\mathrm {v\!+\!g}$
-sites and
$\mathrm {v\!+\!g}$
-sites and
![]() $l(X)$
is
$l(X)$
is
![]() $\mathrm {v\!+\!g}$
-locally closed in
$\mathrm {v\!+\!g}$
-locally closed in
![]() $l(V'\times {\Gamma ^m_{\infty } })$
. So there is a
$l(V'\times {\Gamma ^m_{\infty } })$
. So there is a
![]() $\mathrm {v\!+\!g}$
-closed subset Z of
$\mathrm {v\!+\!g}$
-closed subset Z of
![]() $l(V'\times {\Gamma ^m_{\infty } })$
such that
$l(V'\times {\Gamma ^m_{\infty } })$
such that
![]() $l(X)$
is
$l(X)$
is
![]() $\mathrm {v\!+\!g}$
-open in Z since
$\mathrm {v\!+\!g}$
-open in Z since
![]() $l(V'\times {\Gamma ^m_{\infty } })$
is
$l(V'\times {\Gamma ^m_{\infty } })$
is
![]() $\mathrm {v\!+\!g}$
-closed in
$\mathrm {v\!+\!g}$
-closed in
![]() $V'\times [0,\infty ]^{2m}$
, and Z and
$V'\times [0,\infty ]^{2m}$
, and Z and
![]() $Z\setminus l(X)$
are bounded and
$Z\setminus l(X)$
are bounded and
![]() $\mathrm {v\!+\!g}$
-closed subsets of
$\mathrm {v\!+\!g}$
-closed subsets of
![]() $V'\times {\Gamma } _{\infty }^{2m}$
. Let
$V'\times {\Gamma } _{\infty }^{2m}$
. Let
![]() $P=l^{-1}(Z)$
and
$P=l^{-1}(Z)$
and
![]() $Q=l^{-1}(Z\setminus l(X))$
. Then applying [Reference Hrushovski and Loeser35, Lemma 4.2.6] to the surjective definable maps
$Q=l^{-1}(Z\setminus l(X))$
. Then applying [Reference Hrushovski and Loeser35, Lemma 4.2.6] to the surjective definable maps
![]() $l^{-1}:Z\to l^{-1}(Z)$
and
$l^{-1}:Z\to l^{-1}(Z)$
and
![]() $l^{-1}:Z\setminus l(X)\to l^{-1}(Z\setminus l(X))$
, we see that
$l^{-1}:Z\setminus l(X)\to l^{-1}(Z\setminus l(X))$
, we see that
![]() $\widehat {P}=\widehat {l^{-1}}(\widehat {Z})$
and
$\widehat {P}=\widehat {l^{-1}}(\widehat {Z})$
and
![]() $\widehat {Q}=\widehat {l^{-1}}(\widehat {Z\setminus l(X)})$
; hence they are definably compact by Remark 5.23 and [Reference Hrushovski and Loeser35, Proposition 4.2.9]. Hence, P and Q are bounded
$\widehat {Q}=\widehat {l^{-1}}(\widehat {Z\setminus l(X)})$
; hence they are definably compact by Remark 5.23 and [Reference Hrushovski and Loeser35, Proposition 4.2.9]. Hence, P and Q are bounded
![]() $\mathrm {v\!+\!g}$
-closed subsets (Remark 5.23), X is
$\mathrm {v\!+\!g}$
-closed subsets (Remark 5.23), X is
![]() $\mathrm {v\!+\!g}$
-open in P and
$\mathrm {v\!+\!g}$
-open in P and
![]() $Q=P\setminus X$
.
$Q=P\setminus X$
.
The last statement of the lemma is clear.
Lemma 6.27. If
![]() $X\subseteq V\times {\Gamma ^m_{\infty } }$
is a
$X\subseteq V\times {\Gamma ^m_{\infty } }$
is a
![]() $\mathrm {v\!+\!g}$
-locally closed subset, then
$\mathrm {v\!+\!g}$
-locally closed subset, then
![]() ${\mathcal X}\subseteq {\Gamma ^k_{\infty } }$
is a definably locally closed subset.
${\mathcal X}\subseteq {\Gamma ^k_{\infty } }$
is a definably locally closed subset.
Proof. Let
![]() $V'$
be a projective variety such that V is an open subset of
$V'$
be a projective variety such that V is an open subset of
![]() $V'$
. Then X is still a
$V'$
. Then X is still a
![]() $\mathrm {v\!+\!g}$
-locally closed subset of
$\mathrm {v\!+\!g}$
-locally closed subset of
![]() $V'\times {\Gamma ^m_{\infty } }$
. By Lemma 6.26, let P and Q be bounded
$V'\times {\Gamma ^m_{\infty } }$
. By Lemma 6.26, let P and Q be bounded
![]() $\mathrm {v\!+\!g}$
-closed subsets such that X is
$\mathrm {v\!+\!g}$
-closed subsets such that X is
![]() $\mathrm {v\!+\!g}$
-open in P and
$\mathrm {v\!+\!g}$
-open in P and
![]() $Q=P\setminus X$
.
$Q=P\setminus X$
.
Now we may assume that the pro-definable deformation retraction
![]() $H:I\times \widehat {X}\to \widehat {X}$
is the restriction of a pro-definable deformation retraction
$H:I\times \widehat {X}\to \widehat {X}$
is the restriction of a pro-definable deformation retraction
![]() $H:I\times \widehat {V'}\to \widehat {V'}$
preserving V, P, X and Q. Let
$H:I\times \widehat {V'}\to \widehat {V'}$
preserving V, P, X and Q. Let
![]() ${\mathfrak P}$
,
${\mathfrak P}$
,
![]() ${\mathfrak Q}$
(and
${\mathfrak Q}$
(and
![]() ${\mathfrak X}$
) be the images under H of
${\mathfrak X}$
) be the images under H of
![]() $\widehat {P}$
,
$\widehat {P}$
,
![]() $\widehat {Q}$
(and
$\widehat {Q}$
(and
![]() $\widehat {X}$
), respectively. Then
$\widehat {X}$
), respectively. Then
![]() ${\mathfrak P}$
,
${\mathfrak P}$
,
![]() ${\mathfrak Q}$
and
${\mathfrak Q}$
and
![]() ${\mathfrak X}$
are iso-definable subsets of
${\mathfrak X}$
are iso-definable subsets of
![]() $\widehat {V'}$
, so
$\widehat {V'}$
, so
![]() ${\mathfrak Q}$
and
${\mathfrak Q}$
and
![]() ${\mathfrak X}$
are iso-definable subsets of
${\mathfrak X}$
are iso-definable subsets of
![]() ${\mathfrak P}$
. Let
${\mathfrak P}$
. Let
![]() $h:{\mathfrak P}\to {\mathcal P}$
be a pro-definable homeomorphism between
$h:{\mathfrak P}\to {\mathcal P}$
be a pro-definable homeomorphism between
![]() ${\mathfrak P}$
and a definable subset
${\mathfrak P}$
and a definable subset
![]() ${\mathcal P}$
of
${\mathcal P}$
of
![]() ${\Gamma ^k_{\infty } }$
. Then
${\Gamma ^k_{\infty } }$
. Then
![]() ${\mathcal Q}=h({\mathfrak Q})$
and
${\mathcal Q}=h({\mathfrak Q})$
and
![]() ${\mathcal X}=h({\mathfrak X})$
are definable subsets of
${\mathcal X}=h({\mathfrak X})$
are definable subsets of
![]() ${\mathcal P}$
. By [Reference Hrushovski and Loeser35, Proposition 4.2.9],
${\mathcal P}$
. By [Reference Hrushovski and Loeser35, Proposition 4.2.9],
![]() ${\mathcal P}$
and
${\mathcal P}$
and
![]() ${\mathcal Q}$
are definably compact definable subsets of
${\mathcal Q}$
are definably compact definable subsets of
![]() ${\Gamma ^k_{\infty } }$
; in particular, they are closed. Thus,
${\Gamma ^k_{\infty } }$
; in particular, they are closed. Thus,
![]() ${\mathcal X}={\mathcal P}\setminus {\mathcal Q}$
is an open definable subset of a closed definable subset: that is, it is definably locally closed.
${\mathcal X}={\mathcal P}\setminus {\mathcal Q}$
is an open definable subset of a closed definable subset: that is, it is definably locally closed.
As above, let
![]() $H\colon I\times \widehat {X}\to \widehat {X}$
be a continuous pro-definable deformation retraction with image an iso-definable subset
$H\colon I\times \widehat {X}\to \widehat {X}$
be a continuous pro-definable deformation retraction with image an iso-definable subset
![]() ${\mathfrak X} $
of
${\mathfrak X} $
of
![]() $\widehat {X}$
for which there is a pro-definable homeomorphism
$\widehat {X}$
for which there is a pro-definable homeomorphism
![]() $h\colon {\mathfrak X}\to \mathcal {X}$
with a definable subset
$h\colon {\mathfrak X}\to \mathcal {X}$
with a definable subset
![]() ${\mathcal X}$
of
${\mathcal X}$
of
![]() ${\Gamma ^k_{\infty } }$
. Then we have a retraction
${\Gamma ^k_{\infty } }$
. Then we have a retraction
![]() $r=H\circ i_1\colon \widehat {X}\to {\mathfrak X}$
, where
$r=H\circ i_1\colon \widehat {X}\to {\mathfrak X}$
, where
![]() $i_1\colon \widehat {X}\to I\times {\widehat X}$
is the natural inclusion
$i_1\colon \widehat {X}\to I\times {\widehat X}$
is the natural inclusion
![]() $\widehat {X}\to \{e_I\}\times \widehat {X}$
, where
$\widehat {X}\to \{e_I\}\times \widehat {X}$
, where
![]() $e_I$
is the end point of I.
$e_I$
is the end point of I.
As in [Reference Hrushovski and Loeser35, Remark 11.1.3 (5)], we have:
Remark 6.28. The pro-definable retraction
![]() $\widehat {X}\to {\mathfrak X}$
and the pro-definable homeomorphism
$\widehat {X}\to {\mathfrak X}$
and the pro-definable homeomorphism
![]() $h\colon {\mathfrak X}\to \mathcal {X}$
can be assumed to be definably proper: that is, the pullback of a definably compact set is definably compact.
$h\colon {\mathfrak X}\to \mathcal {X}$
can be assumed to be definably proper: that is, the pullback of a definably compact set is definably compact.
Indeed, since
![]() $h\colon {\mathfrak X} \to {\mathcal X}$
is a pro-definable homeomorphism, it is definably proper. On the other hand, take
$h\colon {\mathfrak X} \to {\mathcal X}$
is a pro-definable homeomorphism, it is definably proper. On the other hand, take
![]() $V'$
a projective variety such that V is an open subset of
$V'$
a projective variety such that V is an open subset of
![]() $V'$
, and assume that the pro-definable deformation retraction
$V'$
, and assume that the pro-definable deformation retraction
![]() $H:I\times \widehat {X}\to \widehat {X}$
is the restriction of a pro-definable deformation retraction
$H:I\times \widehat {X}\to \widehat {X}$
is the restriction of a pro-definable deformation retraction
![]() $H:I\times \widehat {V'}\to \widehat {V'}$
. If
$H:I\times \widehat {V'}\to \widehat {V'}$
. If
![]() ${\mathfrak V}'$
is the image of
${\mathfrak V}'$
is the image of
![]() $H:I\times \widehat {V'}\to \widehat {V'}$
, then the retraction
$H:I\times \widehat {V'}\to \widehat {V'}$
, then the retraction
![]() $\widehat {V'}\to {\mathfrak V}'$
is definably proper; hence its restriction
$\widehat {V'}\to {\mathfrak V}'$
is definably proper; hence its restriction
![]() $\widehat {X}\to {\mathfrak X}$
is also.
$\widehat {X}\to {\mathfrak X}$
is also.
Remark 6.29. Let
![]() $X\subseteq V\times {\Gamma ^m_{\infty } }$
be a definable subset. Below, we denote by c the family of
$X\subseteq V\times {\Gamma ^m_{\infty } }$
be a definable subset. Below, we denote by c the family of
![]() $\mathrm {v\!+\!g}$
-supports on X whose elements are the closed
$\mathrm {v\!+\!g}$
-supports on X whose elements are the closed
![]() $\mathrm {v\!+\!g}$
-subsets of X each contained in some bounded
$\mathrm {v\!+\!g}$
-subsets of X each contained in some bounded
![]() $\mathrm {v\!+\!g}$
-closed subset of X. We will also denote by c the family of
$\mathrm {v\!+\!g}$
-closed subset of X. We will also denote by c the family of
![]() $\widehat {\mathrm {v\!+\!g}}$
-supports on
$\widehat {\mathrm {v\!+\!g}}$
-supports on
![]() $\widehat {X}$
whose elements are the definably compact definable subsets of
$\widehat {X}$
whose elements are the definably compact definable subsets of
![]() $\widehat {X}$
.
$\widehat {X}$
.
Note the following:
-
• The isomorphism of sites
 $\widehat {X}_{\widehat {\mathrm {v\!+\!g}}}\to X_{\mathrm {v\!+\!g}}$
is a morphism in
$\widehat {X}_{\widehat {\mathrm {v\!+\!g}}}\to X_{\mathrm {v\!+\!g}}$
is a morphism in
 ${\mathfrak T}$
, and the inverse image of the family c of
${\mathfrak T}$
, and the inverse image of the family c of
 $\mathrm {v\!+\!g}$
-supports of X is the family c of
$\mathrm {v\!+\!g}$
-supports of X is the family c of
 $\widehat {\mathrm {v\!+\!g}}$
-supports on
$\widehat {\mathrm {v\!+\!g}}$
-supports on
 $\widehat {X}$
. This follows from Remark 5.23 and the fact that a definable subset of
$\widehat {X}$
. This follows from Remark 5.23 and the fact that a definable subset of
 $\widehat {X}$
is the same as a
$\widehat {X}$
is the same as a
 $\widehat {\mathrm {v\!+\!g}}$
-subset of
$\widehat {\mathrm {v\!+\!g}}$
-subset of
 $\widehat {X}$
. Hence the isomorphism of sites
$\widehat {X}$
. Hence the isomorphism of sites
 $\widehat {X}_{\widehat {\mathrm {v\!+\!g}}}\to X_{\mathrm {v\!+\!g}}$
induces an isomorphism in cohomology
$\widehat {X}_{\widehat {\mathrm {v\!+\!g}}}\to X_{\mathrm {v\!+\!g}}$
induces an isomorphism in cohomology  $$ \begin{align*} H^*_c(X;{\mathcal{F}})\simeq H^*_c(\widehat{X};\widehat{{\mathcal{F}}}). \end{align*} $$
$$ \begin{align*} H^*_c(X;{\mathcal{F}})\simeq H^*_c(\widehat{X};\widehat{{\mathcal{F}}}). \end{align*} $$
-
• If X is a
 $\mathrm {v\!+\!g}$
-locally closed subset, then the family c of
$\mathrm {v\!+\!g}$
-locally closed subset, then the family c of
 $\widehat {\mathrm {v\!+\!g}}$
-supports on
$\widehat {\mathrm {v\!+\!g}}$
-supports on
 $\widehat {X}$
is a family of
$\widehat {X}$
is a family of
 $\widehat {\mathrm {v\!+\!g}}$
-normal supports on
$\widehat {\mathrm {v\!+\!g}}$
-normal supports on
 $\widehat {X}$
. Indeed, let
$\widehat {X}$
. Indeed, let
 $V'$
be a projective variety having V as an open subset. By Corollary 5.31,
$V'$
be a projective variety having V as an open subset. By Corollary 5.31,
 $V'\times {\Gamma ^m_{\infty } }$
is weakly
$V'\times {\Gamma ^m_{\infty } }$
is weakly
 $\mathrm {v\!+\!g}$
-normal, so P, being a
$\mathrm {v\!+\!g}$
-normal, so P, being a
 $\mathrm {v\!+\!g}$
-closed subset of
$\mathrm {v\!+\!g}$
-closed subset of
 $V'\times {\Gamma ^m_{\infty } }$
(by Lemma 6.26), is also weakly
$V'\times {\Gamma ^m_{\infty } }$
(by Lemma 6.26), is also weakly
 $\mathrm {v\!+\!g}$
-normal. Since X is a
$\mathrm {v\!+\!g}$
-normal. Since X is a
 $\mathrm {v\!+\!g}$
-open subset of P and every bounded
$\mathrm {v\!+\!g}$
-open subset of P and every bounded
 $\mathrm {v\!+\!g}$
-closed subset of X is also a
$\mathrm {v\!+\!g}$
-closed subset of X is also a
 $\mathrm {v\!+\!g}$
-closed subset of P, the result follows from Definition 3.14 (2).
$\mathrm {v\!+\!g}$
-closed subset of P, the result follows from Definition 3.14 (2).
It follows from the last two remarks that:
Remark 6.30. If
![]() $X\subseteq V\times {\Gamma ^m_{\infty } }$
is a
$X\subseteq V\times {\Gamma ^m_{\infty } }$
is a
![]() $\mathrm {v\!+\!g}$
-locally closed definable subset, then we have induced homomorphisms
$\mathrm {v\!+\!g}$
-locally closed definable subset, then we have induced homomorphisms
and
which are isomorphisms. In particular,
Indeed, let
![]() $j\colon {\mathfrak X}\to \widehat {X}$
be the inclusion. Since
$j\colon {\mathfrak X}\to \widehat {X}$
be the inclusion. Since
![]() ${\mathfrak X}=H(e_I, \widehat {X})$
, we have
${\mathfrak X}=H(e_I, \widehat {X})$
, we have
![]() $r\circ j=\mathrm {id} _{{\mathfrak X}}$
; and as usual, H is a homotopy between
$r\circ j=\mathrm {id} _{{\mathfrak X}}$
; and as usual, H is a homotopy between
![]() $j\circ r$
and
$j\circ r$
and
![]() $\mathrm {id} _{\widehat {X}}$
. Moreover, since H is a morphism of
$\mathrm {id} _{\widehat {X}}$
. Moreover, since H is a morphism of
![]() $\widehat {\mathrm {v\!+\!g}}$
-sites (Lemma 6.24), we also have that
$\widehat {\mathrm {v\!+\!g}}$
-sites (Lemma 6.24), we also have that
![]() $r\circ j$
and
$r\circ j$
and
![]() $j\circ r$
are morphisms of
$j\circ r$
are morphisms of
![]() $\widehat {\mathrm {v\!+\!g}}$
-sites. Since
$\widehat {\mathrm {v\!+\!g}}$
-sites. Since
![]() ${\mathfrak X}=r(\widehat {X})$
, we get that
${\mathfrak X}=r(\widehat {X})$
, we get that
![]() $r^*$
is an isomorphism by homotopy axiom (Theorem 6.8);
$r^*$
is an isomorphism by homotopy axiom (Theorem 6.8);
![]() $h^*$
is an isomorphism since h is a pro-definable homomorphism.
$h^*$
is an isomorphism since h is a pro-definable homomorphism.
Note that by the same argument, taking the family of
![]() $\mathrm {v\!+\!g}$
-supports given by the
$\mathrm {v\!+\!g}$
-supports given by the
![]() $\mathrm {v\!+\!g}$
-closed subsets, we get, for any definable subset
$\mathrm {v\!+\!g}$
-closed subsets, we get, for any definable subset
![]() $X\subseteq V\times {\Gamma ^m_{\infty } }$
, an isomorphism
$X\subseteq V\times {\Gamma ^m_{\infty } }$
, an isomorphism
Theorem 6.31. Let A be a noetherian ring, and let L be a finitely generated A-module. Let V be a variety. If
![]() $X\subseteq V\times {\Gamma ^m_{\infty } }$
is a
$X\subseteq V\times {\Gamma ^m_{\infty } }$
is a
![]() $\mathrm {v\!+\!g}$
-locally closed definable subset, then
$\mathrm {v\!+\!g}$
-locally closed definable subset, then
![]() $H^p_c(X;L_X)\simeq H^p_c(\widehat {X};L_{\widehat {X}})$
is finitely generated for each p.
$H^p_c(X;L_X)\simeq H^p_c(\widehat {X};L_{\widehat {X}})$
is finitely generated for each p.
Proof. The variety V is a finite union of open quasi-projective subvarieties
![]() $V_1, \ldots , V_n$
, and the result follows by induction on
$V_1, \ldots , V_n$
, and the result follows by induction on
![]() $n.$
In the case
$n.$
In the case
![]() $n=1$
, the variety V is quasi-projective, and since
$n=1$
, the variety V is quasi-projective, and since
![]() $\mathcal {X}$
is definably locally closed by Lemma 6.27, the result follows from Theorem 6.20 and the isomorphism of Remark 6.30.
$\mathcal {X}$
is definably locally closed by Lemma 6.27, the result follows from Theorem 6.20 and the isomorphism of Remark 6.30.
Now suppose that
![]() $V=V_1\cup \cdots \cup V_{n+1}$
, and, by the induction hypothesis, the result holds for
$V=V_1\cup \cdots \cup V_{n+1}$
, and, by the induction hypothesis, the result holds for
![]() $U=V_1\cup \cdots \cup V_n$
. Let
$U=V_1\cup \cdots \cup V_n$
. Let
![]() $Y=X\cap (U\times {\Gamma ^m_{\infty } })$
and
$Y=X\cap (U\times {\Gamma ^m_{\infty } })$
and
![]() $Z=X\cap (V_{n+1}\times {\Gamma ^m_{\infty } })$
. Then Y (respectively, Z) is a
$Z=X\cap (V_{n+1}\times {\Gamma ^m_{\infty } })$
. Then Y (respectively, Z) is a
![]() $\mathrm {v\!+\!g}$
-locally closed definable subset of
$\mathrm {v\!+\!g}$
-locally closed definable subset of
![]() $U\times {\Gamma ^m_{\infty } }$
(respectively,
$U\times {\Gamma ^m_{\infty } }$
(respectively,
![]() $V_{n+1}\times {\Gamma ^m_{\infty } }$
) and
$V_{n+1}\times {\Gamma ^m_{\infty } }$
) and
![]() $H^p_c(Y;L_Y)$
(respectively, is
$H^p_c(Y;L_Y)$
(respectively, is
![]() $H^p_c(Z;L_Z)$
) finitely generated for each p. Also note that
$H^p_c(Z;L_Z)$
) finitely generated for each p. Also note that
![]() $Y\cap Z$
is a
$Y\cap Z$
is a
![]() $\mathrm {v\!+\!g}$
-locally closed definable subset of
$\mathrm {v\!+\!g}$
-locally closed definable subset of
![]() $V_{n+1}\times {\Gamma ^m_{\infty } }$
and
$V_{n+1}\times {\Gamma ^m_{\infty } }$
and
![]() $H^p_c(Y\cap Z;L_{Y\cap Z})$
finitely generated for each p.
$H^p_c(Y\cap Z;L_{Y\cap Z})$
finitely generated for each p.
Since
![]() $Y, Z$
and
$Y, Z$
and
![]() $Y\cap Z$
are
$Y\cap Z$
are
![]() $\mathrm {v\!+\!g}$
-locally closed subsets of X, the short exact coefficients sequence
$\mathrm {v\!+\!g}$
-locally closed subsets of X, the short exact coefficients sequence
together with Corollary 3.27 gives the Mayer-Vietoris sequence
It also follows that
![]() $\ker \beta =\mathrm {Im}\,\alpha $
is finitely generated and
$\ker \beta =\mathrm {Im}\,\alpha $
is finitely generated and
![]() $\mathrm {Im}\,\beta $
is finitely generated. Thus we see that
$\mathrm {Im}\,\beta $
is finitely generated. Thus we see that
![]() $H^p_c(X;L_X)$
is finitely generated for each p.
$H^p_c(X;L_X)$
is finitely generated for each p.
Let K and
![]() $K'$
be small elementary substructures of
$K'$
be small elementary substructures of
![]() $\mathbb {U}$
, with
$\mathbb {U}$
, with
![]() $K'$
an elementary extension of K. Given a K-definable set X, let, as before,
$K'$
an elementary extension of K. Given a K-definable set X, let, as before,
![]() $H\colon I\times \widehat {X}\to \widehat {X}$
be a continuous pro-definable deformation retraction with image an iso-definable subset
$H\colon I\times \widehat {X}\to \widehat {X}$
be a continuous pro-definable deformation retraction with image an iso-definable subset
![]() ${\mathfrak X} $
of
${\mathfrak X} $
of
![]() $\widehat {X}$
for which there is a pro-definable homeomorphism
$\widehat {X}$
for which there is a pro-definable homeomorphism
![]() $h\colon {\mathfrak X}\to \mathcal {X}$
with a K-definable subset
$h\colon {\mathfrak X}\to \mathcal {X}$
with a K-definable subset
![]() ${\mathcal X}$
of
${\mathcal X}$
of
![]() ${\Gamma ^k_{\infty } }$
. Then we have commutative diagrams of morphisms of
${\Gamma ^k_{\infty } }$
. Then we have commutative diagrams of morphisms of
![]() $\widehat {\mathrm {v\!+\!g}}$
-sites
$\widehat {\mathrm {v\!+\!g}}$
-sites

and

where the vertical arrows are the morphisms of
![]() $\widehat {\mathrm {v\!+\!g}}$
-sites taking
$\widehat {\mathrm {v\!+\!g}}$
-sites taking
![]() $\widehat {U}(K)$
to
$\widehat {U}(K)$
to
![]() $\widehat {U}(K')$
.
$\widehat {U}(K')$
.
Note that
![]() $H^{K'}\colon I(K')\times \widehat {X}(K') \to \widehat {X}(K')$
is a continuous pro-definable deformation retraction with image an iso-definable subset
$H^{K'}\colon I(K')\times \widehat {X}(K') \to \widehat {X}(K')$
is a continuous pro-definable deformation retraction with image an iso-definable subset
![]() ${\mathfrak X}(K')$
of
${\mathfrak X}(K')$
of
![]() $\widehat {X}(K')$
and
$\widehat {X}(K')$
and
![]() $h^{K'}\colon {\mathfrak X}(K')\to \mathcal {X}(K')$
is a pro-definable homeomorphism to a K-definable subset
$h^{K'}\colon {\mathfrak X}(K')\to \mathcal {X}(K')$
is a pro-definable homeomorphism to a K-definable subset
![]() ${\mathcal X}(K')$
of
${\mathcal X}(K')$
of
![]() ${\Gamma ^k_{\infty } }(K')$
. Furthermore, if X is a
${\Gamma ^k_{\infty } }(K')$
. Furthermore, if X is a
![]() $\mathrm {v\!+\!g}$
-locally closed definable subset, then
$\mathrm {v\!+\!g}$
-locally closed definable subset, then
![]() $X(K')$
is also. Similar remarks hold for K in place of
$X(K')$
is also. Similar remarks hold for K in place of
![]() $K'$
.
$K'$
.
Theorem 6.32. Let V be a variety over K. Let
![]() $K'$
be an elementary extension of K. If
$K'$
be an elementary extension of K. If
![]() $X\subseteq V\times {\Gamma ^m_{\infty } }$
is a
$X\subseteq V\times {\Gamma ^m_{\infty } }$
is a
![]() $\mathrm {v\!+\!g}$
-locally closed K-definable subset, then for every
$\mathrm {v\!+\!g}$
-locally closed K-definable subset, then for every
![]() ${\mathcal {F}}\in \mathrm {Mod}(A_{X(K)_{\mathrm {v\!+\!g}}})$
, we have an isomorphism
${\mathcal {F}}\in \mathrm {Mod}(A_{X(K)_{\mathrm {v\!+\!g}}})$
, we have an isomorphism
Proof. First let us prove that for every
![]() $\mathrm {v\!+\!g}$
-locally closed K-definable subset
$\mathrm {v\!+\!g}$
-locally closed K-definable subset
![]() $X\subseteq V\times {\Gamma ^m_{\infty } }$
, we have an isomorphism
$X\subseteq V\times {\Gamma ^m_{\infty } }$
, we have an isomorphism
The variety V is a finite union of open quasi-projective subvarieties
![]() $V_1, \ldots , V_n$
, and the result follows by induction on
$V_1, \ldots , V_n$
, and the result follows by induction on
![]() $n.$
In the case
$n.$
In the case
![]() $n=1$
, the variety V is quasi-projective, and the result follows from the observations above, Remark 6.30 and Theorem 6.22 taken in K and in
$n=1$
, the variety V is quasi-projective, and the result follows from the observations above, Remark 6.30 and Theorem 6.22 taken in K and in
![]() $K'$
.
$K'$
.
The inductive step is obtained from the following commutative diagram with the Mayer-Vietoris sequences as in the proof of Theorem 6.31 taken in K and in
![]() $K'$
, the inductive hypothesis and the five lemmas:
$K'$
, the inductive hypothesis and the five lemmas:

By Lemma 6.26, let P be a definably compact
![]() $\mathrm {v\!+\!g}$
-closed subset such that
$\mathrm {v\!+\!g}$
-closed subset such that
![]() $X\subseteq P$
is a
$X\subseteq P$
is a
![]() $\mathrm {v\!+\!g}$
-open subset. Note that P is defined over K. It follows from the above that for every
$\mathrm {v\!+\!g}$
-open subset. Note that P is defined over K. It follows from the above that for every
![]() $\mathrm {v\!+\!g}$
-closed subset Z of P, defined over K, we have
$\mathrm {v\!+\!g}$
-closed subset Z of P, defined over K, we have
With this setup, the rest of the proof is exactly the same as that of Theorem 6.22 using Corollary 3.27, Remark 5.23 instead of Remark 4.11 and Lemma 6.21.
Remark 6.33. Note that for the cohomologies
![]() $H^*(X;L_X)$
and
$H^*(X;L_X)$
and
![]() $H^*(X;{\mathcal {F}})$
without supports, we could also get finiteness and invariance results, respectively, if we knew the corresponding results in
$H^*(X;{\mathcal {F}})$
without supports, we could also get finiteness and invariance results, respectively, if we knew the corresponding results in
![]() ${\mathbf {\Gamma }_{\infty } }$
. Indeed, by the isomorphism
${\mathbf {\Gamma }_{\infty } }$
. Indeed, by the isomorphism
![]() $H^*(X;L_X)\simeq H^*(\mathcal {X};L_{\mathcal {X}})$
of Remark 6.30, in the quasi-projective case, we would get the finiteness and invariance results for any definable subset
$H^*(X;L_X)\simeq H^*(\mathcal {X};L_{\mathcal {X}})$
of Remark 6.30, in the quasi-projective case, we would get the finiteness and invariance results for any definable subset
![]() $X\subseteq V\times {\Gamma ^m_{\infty } }$
. For the general case, X would have to be assumed
$X\subseteq V\times {\Gamma ^m_{\infty } }$
. For the general case, X would have to be assumed
![]() $\mathrm {v\!+\!g}$
-normal (in order to use Corollary 3.27), and the result would follow by exactly the same arguments as above.
$\mathrm {v\!+\!g}$
-normal (in order to use Corollary 3.27), and the result would follow by exactly the same arguments as above.
6.4 Vanishing of cohomology
Below are a couple of quick remarks about vanishing of cohomology in our setting.
By the isomorphisms of Remark 6.30 and Theorem 6.20, we immediately obtain:
Theorem 6.34. Let V be a quasi-projective variety. If
![]() $X\subseteq V\times {\Gamma ^m_{\infty } }$
is a
$X\subseteq V\times {\Gamma ^m_{\infty } }$
is a
![]() $\mathrm {v\!+\!g}$
-locally closed subset, then
$\mathrm {v\!+\!g}$
-locally closed subset, then
![]() $H^p_c(X;L_X)=0$
for all
$H^p_c(X;L_X)=0$
for all
![]() $p> \dim {\mathcal X}$
. In particular,
$p> \dim {\mathcal X}$
. In particular,
![]() $H^p_c(X;L_X)=0$
for all
$H^p_c(X;L_X)=0$
for all
![]() $p> \dim {X}$
.
$p> \dim {X}$
.
![]() $\Box $
$\Box $
When there is a good notion of dimension (recall Remark 6.5), we can obtain the following results.
Theorem 6.35. Let X be a definable subset of a variety V. If X is
![]() $\mathrm {v\!+\!g}$
-normal, then
$\mathrm {v\!+\!g}$
-normal, then
![]() $H^p(X;{\mathcal {F}})=0$
for every
$H^p(X;{\mathcal {F}})=0$
for every
![]() $p>\dim (\overline {X}^{\mathrm {Zar}})$
and every
$p>\dim (\overline {X}^{\mathrm {Zar}})$
and every
![]() ${\mathcal {F}}\in \mathrm {Mod} (A_{X_{\mathrm {v\!+\!g}}})$
, where
${\mathcal {F}}\in \mathrm {Mod} (A_{X_{\mathrm {v\!+\!g}}})$
, where
![]() $\overline {X}^{\mathrm {Zar}}$
denotes the Zariski closure of X.
$\overline {X}^{\mathrm {Zar}}$
denotes the Zariski closure of X.
Proof. Going to
![]() $\widetilde {\widehat {X}}$
, we obtain a normal spectral space, and the result follows from [Reference Coste and Roy15, Corollary 6] since
$\widetilde {\widehat {X}}$
, we obtain a normal spectral space, and the result follows from [Reference Coste and Roy15, Corollary 6] since
![]() $\dim _{\mathrm {Krull}}(\widetilde {\widehat {X}})$
: that is, the maximal length of a chain of proper specialisations of points in
$\dim _{\mathrm {Krull}}(\widetilde {\widehat {X}})$
: that is, the maximal length of a chain of proper specialisations of points in
![]() $\widetilde {\widehat {X}}$
is bounded by
$\widetilde {\widehat {X}}$
is bounded by
![]() $\dim (\overline {X}^{\mathrm {Zar}})$
by Corollary 6.4.
$\dim (\overline {X}^{\mathrm {Zar}})$
by Corollary 6.4.
Based on Propositions 3.24, 3.26 and 3.31 together with Theorem 6.35, the proof of the following result is classical. Compare with [Reference Edmundo and Prelli25, Theorem 3.12] in the o-minimal case, with [Reference Delfs17, Corollary 9.4] in the locally semi-algebraic case or with [Reference Bredon14, Chapter II, 16.2 and 16.4] in the topological case.
Theorem 6.36. Let V be a variety. If X is a
![]() $\mathrm {v\!+\!g}$
-locally closed subset of V, then
$\mathrm {v\!+\!g}$
-locally closed subset of V, then
![]() $H^p_c(X;{\mathcal {F}})=0$
for every
$H^p_c(X;{\mathcal {F}})=0$
for every
![]() $p>\dim (\overline {X}^{\mathrm {Zar}})$
and every
$p>\dim (\overline {X}^{\mathrm {Zar}})$
and every
![]() ${\mathcal {F}}\in \mathrm {Mod} (A_{X_{\mathrm {v\!+\!g}}})$
.
${\mathcal {F}}\in \mathrm {Mod} (A_{X_{\mathrm {v\!+\!g}}})$
.
Proof. We work in
![]() $\widetilde {\widehat {X}}$
and let
$\widetilde {\widehat {X}}$
and let
![]() $n=\dim (\overline {X}^{\mathrm {Zar}})$
. Since the functor
$n=\dim (\overline {X}^{\mathrm {Zar}})$
. Since the functor
![]() $\Gamma _c(X; \bullet )$
is left exact and the full additive subcategory of
$\Gamma _c(X; \bullet )$
is left exact and the full additive subcategory of
![]() $\mathrm {Mod}(A_{\widetilde {\widehat {X}}})$
of c-soft sheaves is
$\mathrm {Mod}(A_{\widetilde {\widehat {X}}})$
of c-soft sheaves is
![]() $\Gamma _c(X; \bullet )$
-injective (Proposition 3.26), by the general result of homological algebra [Reference Kashiwara and Schapira39, Exercise I.19], it is enough to show that if
$\Gamma _c(X; \bullet )$
-injective (Proposition 3.26), by the general result of homological algebra [Reference Kashiwara and Schapira39, Exercise I.19], it is enough to show that if
![]() $0\longrightarrow {\mathcal F}\longrightarrow {\mathcal I}^0\longrightarrow {\mathcal I}^1\longrightarrow \cdots \longrightarrow {\mathcal I}^n\longrightarrow 0$
is an exact sequence of sheaves in
$0\longrightarrow {\mathcal F}\longrightarrow {\mathcal I}^0\longrightarrow {\mathcal I}^1\longrightarrow \cdots \longrightarrow {\mathcal I}^n\longrightarrow 0$
is an exact sequence of sheaves in
![]() $\mathrm {Mod} (A_{\widetilde {\widehat {X}}})$
such that
$\mathrm {Mod} (A_{\widetilde {\widehat {X}}})$
such that
![]() ${\mathcal I}^k$
is c-soft for
${\mathcal I}^k$
is c-soft for
![]() $0\leq k\leq n-1$
, then
$0\leq k\leq n-1$
, then
![]() ${\mathcal I}^n$
is c-soft.
${\mathcal I}^n$
is c-soft.
By Proposition 3.24 (4), it suffices to prove that
![]() ${\mathcal I}^n_{|Z}$
is soft for every constructible subset Z of
${\mathcal I}^n_{|Z}$
is soft for every constructible subset Z of
![]() $\widetilde {\widehat {X}}$
, which is in the normal and constructible family of supports c. Since c is normal, there is a constructible neighbourhood Y of Z in
$\widetilde {\widehat {X}}$
, which is in the normal and constructible family of supports c. Since c is normal, there is a constructible neighbourhood Y of Z in
![]() $\widetilde {\widehat {X}}$
that is in c. If we show that
$\widetilde {\widehat {X}}$
that is in c. If we show that
![]() ${\mathcal I}^n_{|Y}$
is soft, then it will follow that
${\mathcal I}^n_{|Y}$
is soft, then it will follow that
![]() ${\mathcal I}^n_{|Z}$
is soft (Proposition 3.24 (2)).
${\mathcal I}^n_{|Z}$
is soft (Proposition 3.24 (2)).
Let U be an open and constructible subset of Y. By hypothesis and Proposition 3.31, each
![]() $({\mathcal I}^k_{|Y})_U$
is acyclic for
$({\mathcal I}^k_{|Y})_U$
is acyclic for
![]() $0\leq k \leq n-1$
. Let
$0\leq k \leq n-1$
. Let
![]() ${\mathcal Z}^k=\mathrm {ker}(({\mathcal I}^k_{|Y})_U\longrightarrow ({\mathcal I}^{k+1}_{|Y})_U).$
Then the long exact cohomology sequences of the short exact sequences
${\mathcal Z}^k=\mathrm {ker}(({\mathcal I}^k_{|Y})_U\longrightarrow ({\mathcal I}^{k+1}_{|Y})_U).$
Then the long exact cohomology sequences of the short exact sequences
![]() $0\longrightarrow {\mathcal Z}^k\longrightarrow ({\mathcal I}^k_{|Y})_U\longrightarrow {\mathcal Z}^{k+1}\longrightarrow 0$
show that
$0\longrightarrow {\mathcal Z}^k\longrightarrow ({\mathcal I}^k_{|Y})_U\longrightarrow {\mathcal Z}^{k+1}\longrightarrow 0$
show that
Since Y is a normal, constructible open subset of
![]() $\widetilde {\widehat {X}}$
, we have
$\widetilde {\widehat {X}}$
, we have
![]() $H^p(Y;{\mathcal G})=0$
for
$H^p(Y;{\mathcal G})=0$
for
![]() $p>n$
and every sheaf
$p>n$
and every sheaf
![]() ${\mathcal G}$
on Y by Theorem 6.35 applied to an appropriate
${\mathcal G}$
on Y by Theorem 6.35 applied to an appropriate
![]() $\mathrm {v\!+\!g}$
-normal open definable subset of X whose tilde of the hat is Y. Thus
$\mathrm {v\!+\!g}$
-normal open definable subset of X whose tilde of the hat is Y. Thus
![]() $H^1(Y;({\mathcal I}^n_{|Y})_U)=0$
. Since U was an arbitrary open and constructible subset of Y, it follows from Proposition 3.31 that
$H^1(Y;({\mathcal I}^n_{|Y})_U)=0$
. Since U was an arbitrary open and constructible subset of Y, it follows from Proposition 3.31 that
![]() ${\mathcal I}^n_{|Y}$
is soft as required.
${\mathcal I}^n_{|Y}$
is soft as required.
7 Relation with Berkovich spaces
In this section, we relate our results to classical results of Berkovich spaces. Let us first recall the relation – already established in [Reference Hrushovski and Loeser35] – between the stable completion of algebraic varieties and their analytification.
Let
![]() $(F,\mathrm {val})$
be a nonarchimedean valued field of rank 1 (i.e.,
$(F,\mathrm {val})$
be a nonarchimedean valued field of rank 1 (i.e.,
![]() $\mathrm {val} (F)\subseteq \mathbb {R} _{\infty }$
). We allow F to be trivially valued and do not assume it to be complete. Consider
$\mathrm {val} (F)\subseteq \mathbb {R} _{\infty }$
). We allow F to be trivially valued and do not assume it to be complete. Consider
![]() ${\mathbf F}:= (F, \mathbb {R})$
as a substructure of a model of ACVF. Let V be an algebraic variety over F and X be an
${\mathbf F}:= (F, \mathbb {R})$
as a substructure of a model of ACVF. Let V be an algebraic variety over F and X be an
![]() ${\mathbf F}$
-definable subset of V. As in [Reference Hrushovski and Loeser35, Chapter 14], we define
${\mathbf F}$
-definable subset of V. As in [Reference Hrushovski and Loeser35, Chapter 14], we define
![]() $B_{{\mathbf F}}(X)$
, the model-theoretic Berkovich space of X, to be the space of types over
$B_{{\mathbf F}}(X)$
, the model-theoretic Berkovich space of X, to be the space of types over
![]() ${\mathbf F}$
, concentrated on X, which are almost orthogonal to
${\mathbf F}$
, concentrated on X, which are almost orthogonal to
![]() $\mathbb {R}$
. The last condition means that for any
$\mathbb {R}$
. The last condition means that for any
![]() ${\mathbf F}$
-definable map
${\mathbf F}$
-definable map
![]() $h\colon X\to \mathbb {R}_{\infty }$
and for any
$h\colon X\to \mathbb {R}_{\infty }$
and for any
![]() $p\in B_{{\mathbf F}}(X)$
, the push-forward
$p\in B_{{\mathbf F}}(X)$
, the push-forward
![]() $h_*(p)$
is concentrated on a point of
$h_*(p)$
is concentrated on a point of
![]() $\mathbb {R} _{\infty }$
that is denoted by
$\mathbb {R} _{\infty }$
that is denoted by
![]() $h(p)$
. The topology on
$h(p)$
. The topology on
![]() $B_{{\mathbf F}}(X)$
is the topology having as a basis finite unions of finite intersections of sets of the form
$B_{{\mathbf F}}(X)$
is the topology having as a basis finite unions of finite intersections of sets of the form
where U is a Zariski open set of V,
![]() $f\in {\mathcal {O}}_V^{\mathrm {val}}(U)$
and I is an open interval on
$f\in {\mathcal {O}}_V^{\mathrm {val}}(U)$
and I is an open interval on
![]() $\mathbb {R}_{\infty }$
. In addition, the construction is functorial: that is, given a variety
$\mathbb {R}_{\infty }$
. In addition, the construction is functorial: that is, given a variety
![]() $V'$
over F and
$V'$
over F and
![]() ${\mathbf F}$
-definable subset
${\mathbf F}$
-definable subset
![]() $X'$
of
$X'$
of
![]() $V'$
and an
$V'$
and an
![]() ${\mathbf F}$
-definable map
${\mathbf F}$
-definable map
![]() $f\colon X\to X'$
, there is an induced map
$f\colon X\to X'$
, there is an induced map
![]() $B_{{\mathbf F}}(f)\colon B_{{\mathbf F}}(X)\to B_{{\mathbf F}}(X')$
.
$B_{{\mathbf F}}(f)\colon B_{{\mathbf F}}(X)\to B_{{\mathbf F}}(X')$
.
Suppose now that F is complete. As a set, Berkovich’s analytification
![]() $V^{\mathrm {an}}$
of V can be described as pairs
$V^{\mathrm {an}}$
of V can be described as pairs
![]() $(x, u_x)$
with x a point (in the schematic sense) of V and
$(x, u_x)$
with x a point (in the schematic sense) of V and
![]() $u_x\colon F(x)\to \mathbb {R}_{\infty }$
a valuation extending
$u_x\colon F(x)\to \mathbb {R}_{\infty }$
a valuation extending
![]() $\mathrm {val} $
on the residue field
$\mathrm {val} $
on the residue field
![]() $F(x)$
of the stalk at x. The topology on
$F(x)$
of the stalk at x. The topology on
![]() $V^{\mathrm {an}}$
is the coarsest topology such that for every
$V^{\mathrm {an}}$
is the coarsest topology such that for every
![]() $f\in {\mathcal {O}}_V(U)$
, the maps
$f\in {\mathcal {O}}_V(U)$
, the maps
![]() $x\mapsto u_x\circ f_x$
, where
$x\mapsto u_x\circ f_x$
, where
![]() $f_x\in {\mathcal {O}}_{V, x}\simeq F(x)$
are all continuous. By results in [Reference Berkovich8], the topological space
$f_x\in {\mathcal {O}}_{V, x}\simeq F(x)$
are all continuous. By results in [Reference Berkovich8], the topological space
![]() $V^{\mathrm {an}}$
is Hausdorff (recall V is assumed to be separated), locally compact and locally path connected. The induced topology on the subset
$V^{\mathrm {an}}$
is Hausdorff (recall V is assumed to be separated), locally compact and locally path connected. The induced topology on the subset
![]() $V(F)$
coincides with the valuation topology, and if F is algebraically closed, then this subset is dense.
$V(F)$
coincides with the valuation topology, and if F is algebraically closed, then this subset is dense.
As explained in [Reference Hrushovski and Loeser35, Section 14.1], we have:
Fact 7.1. If F is complete, then the model-theoretic Berkovich space
![]() $B_{{\mathbf F}}(V)$
is canonically homeomorphic to
$B_{{\mathbf F}}(V)$
is canonically homeomorphic to
![]() $V^{\mathrm {an}}$
. Moreover, the image of
$V^{\mathrm {an}}$
. Moreover, the image of
![]() $B_{{\mathbf F}}(X)$
in
$B_{{\mathbf F}}(X)$
in
![]() $V^{\mathrm {an}}$
is a semi-algebraic subset in the sense of [Reference Ducros20], and every semi-algebraic subset of
$V^{\mathrm {an}}$
is a semi-algebraic subset in the sense of [Reference Ducros20], and every semi-algebraic subset of
![]() $V^{\mathrm {an}}$
is of this form.
$V^{\mathrm {an}}$
is of this form.
![]() $\Box $
$\Box $
Let us now recall the relation between
![]() $B_{{\mathbf F}}(V)$
and
$B_{{\mathbf F}}(V)$
and
![]() $\widehat {V}$
. Let
$\widehat {V}$
. Let
![]() $F^{max}$
be the unique, up to isomorphism over
$F^{max}$
be the unique, up to isomorphism over
![]() ${\mathbf F}$
, maximally complete algebraically closed field containing F, with value group
${\mathbf F}$
, maximally complete algebraically closed field containing F, with value group
![]() $\mathbb {R}$
and residue field equal to the algebraic closure of the residue field of F. Recall that maximally complete means every family of balls with the finite intersection property has a non-empty intersection. By [Reference Hrushovski and Loeser35, Lemma 14.1.1 and Proposition 14.1.2], we have:
$\mathbb {R}$
and residue field equal to the algebraic closure of the residue field of F. Recall that maximally complete means every family of balls with the finite intersection property has a non-empty intersection. By [Reference Hrushovski and Loeser35, Lemma 14.1.1 and Proposition 14.1.2], we have:
Fact 7.2. There is a continuous surjective closed map
If
![]() $F=F^{max},$
then
$F=F^{max},$
then
![]() $\pi $
is a homeomorphism.
$\pi $
is a homeomorphism.
![]() $\Box $
$\Box $
For the rest of this section, we assume that
![]() $\mathbb {U}$
contains
$\mathbb {U}$
contains
![]() ${\mathbf F}$
and consider only small elementary substructures of
${\mathbf F}$
and consider only small elementary substructures of
![]() $\mathbb {U}$
containing
$\mathbb {U}$
containing
![]() ${\mathbf F}$
.
${\mathbf F}$
.
Remark 7.3. Let X be an
![]() ${\mathbf F}$
-definable subset, and let K and
${\mathbf F}$
-definable subset, and let K and
![]() $K'$
be elementary substructures of
$K'$
be elementary substructures of
![]() $\mathbb {U}$
containing
$\mathbb {U}$
containing
![]() ${\mathbf F}$
. Observe that one can express (over
${\mathbf F}$
. Observe that one can express (over
![]() ${\mathbf F}$
) the fact that
${\mathbf F}$
) the fact that
![]() $X(K)$
is covered by two disjoint
$X(K)$
is covered by two disjoint
![]() $\mathrm {v\!+\!g}$
-open subsets. Therefore, if two such disjoint
$\mathrm {v\!+\!g}$
-open subsets. Therefore, if two such disjoint
![]() $\mathrm {v\!+\!g}$
-open subsets exist in K, they exist in any elementary extension of K containing
$\mathrm {v\!+\!g}$
-open subsets exist in K, they exist in any elementary extension of K containing
![]() ${\mathbf F}$
. By Fact 5.11, this shows that
${\mathbf F}$
. By Fact 5.11, this shows that
![]() $\widehat {X}(K)$
is definably connected if and only if
$\widehat {X}(K)$
is definably connected if and only if
![]() $\widehat {V}(K')$
is definably connected in
$\widehat {V}(K')$
is definably connected in
![]() $K'$
.
$K'$
.
Proposition 7.4. Let X be an
![]() ${\mathbf F}$
-definable subset of an algebraic variety V over F. Then the following are equivalent:
${\mathbf F}$
-definable subset of an algebraic variety V over F. Then the following are equivalent:
-
(1)
 $\widehat {X}$
is definably connected.
$\widehat {X}$
is definably connected. -
(2)
 $\widehat {X}(F^{max})$
is connected.
$\widehat {X}(F^{max})$
is connected.
In addition, if
![]() $\widehat {X}(F^{max})$
is connected, so is
$\widehat {X}(F^{max})$
is connected, so is
![]() $B_{\mathbf {F}}(X)$
. In particular, when F is complete, if
$B_{\mathbf {F}}(X)$
. In particular, when F is complete, if
![]() $\widehat {V}(F^{max})$
is connected, then
$\widehat {V}(F^{max})$
is connected, then
![]() $V^{\mathrm {an}}$
is connected.
$V^{\mathrm {an}}$
is connected.
Proof. By Remark 7.3, (1) above is equivalent to
![]() $\widehat {X}(F^{max})$
being definably connected. Suppose first that V is quasi-projective. By the main theorem of Hrushovski and Loeser [Reference Hrushovski and Loeser35, Theorem 11.1.1], there is a pro-definable deformation retraction of
$\widehat {X}(F^{max})$
being definably connected. Suppose first that V is quasi-projective. By the main theorem of Hrushovski and Loeser [Reference Hrushovski and Loeser35, Theorem 11.1.1], there is a pro-definable deformation retraction of
![]() $\widehat {X}(F^{max})$
to a definable subset
$\widehat {X}(F^{max})$
to a definable subset
![]() ${\mathcal X}$
of
${\mathcal X}$
of
![]() $\mathbb {R}_{\infty }^n$
. Hence,
$\mathbb {R}_{\infty }^n$
. Hence,
![]() $\widehat {X}(F^{max})$
is definably connected (respectively, connected) if and only if
$\widehat {X}(F^{max})$
is definably connected (respectively, connected) if and only if
![]() ${\mathcal X}$
is definably connected (respectively, connected). But
${\mathcal X}$
is definably connected (respectively, connected). But
![]() ${\mathcal X}$
is definably connected if and only if it is connected (the proof in o-minimal expansions of
${\mathcal X}$
is definably connected if and only if it is connected (the proof in o-minimal expansions of
![]() $(\mathbb {R}, <)$
given in [Reference van den Dries53, Chapter III, (2.18) and (2.19) Exercise 7] uses only cell decomposition and works in
$(\mathbb {R}, <)$
given in [Reference van den Dries53, Chapter III, (2.18) and (2.19) Exercise 7] uses only cell decomposition and works in
![]() $\mathbb {R}_{\infty }$
).
$\mathbb {R}_{\infty }$
).
If V is not quasi-projective, consider an open immersion
![]() $V\rightarrow W$
, where W is a complete variety and V is Zariski dense. By Chow’s lemma, there is an epimorphism
$V\rightarrow W$
, where W is a complete variety and V is Zariski dense. By Chow’s lemma, there is an epimorphism
![]() $f\colon W'\to W$
, where
$f\colon W'\to W$
, where
![]() $W'$
is a projective variety. Consider the quasi-projective variety
$W'$
is a projective variety. Consider the quasi-projective variety
![]() $V'=f^{-1}(V)$
, and let
$V'=f^{-1}(V)$
, and let
![]() $X'=f^{-1}(X) \subseteq V'$
. By Lemma 5.21,
$X'=f^{-1}(X) \subseteq V'$
. By Lemma 5.21,
![]() $\widehat {X'}(F^{max})$
has finitely many definably connected components, say
$\widehat {X'}(F^{max})$
has finitely many definably connected components, say
![]() $C^{\prime }_1, \ldots , C^{\prime }_k$
, which by the above are also the finitely many connected components of the topological space
$C^{\prime }_1, \ldots , C^{\prime }_k$
, which by the above are also the finitely many connected components of the topological space
![]() $\widehat {X'}(F^{max})$
. The image
$\widehat {X'}(F^{max})$
. The image
![]() $C_i$
of each connected component
$C_i$
of each connected component
![]() $C^{\prime }_i$
of
$C^{\prime }_i$
of
![]() $\widehat {X'}(F^{max})$
under the restriction of
$\widehat {X'}(F^{max})$
under the restriction of
![]() $f_|$
is a connected subset of
$f_|$
is a connected subset of
![]() $\widehat {X}(F^{max})$
. Note that these connected subsets of
$\widehat {X}(F^{max})$
. Note that these connected subsets of
![]() $\widehat {X}(F^{max})$
are also definably connected subsets.
$\widehat {X}(F^{max})$
are also definably connected subsets.
Now we follow the idea in the proof of [Reference van den Dries53, Chapter III, (2.18)], as above in
![]() $\mathbb {R} _{\infty }$
with cells for the
$\mathbb {R} _{\infty }$
with cells for the
![]() $C_i$
s, to show that some union of the
$C_i$
s, to show that some union of the
![]() $C_i$
s is both a definably connected component and a connected component of
$C_i$
s is both a definably connected component and a connected component of
![]() $\widehat {X}(F^{max})$
. From there, it follows that
$\widehat {X}(F^{max})$
. From there, it follows that
![]() $\widehat {X}(F^{max})$
is definably connected if and only if it is connected. Let us construct inductively a sequence
$\widehat {X}(F^{max})$
is definably connected if and only if it is connected. Let us construct inductively a sequence
![]() $i_1,\ldots , i_j,\ldots $
such that for each j,
$i_1,\ldots , i_j,\ldots $
such that for each j,
![]() $\bigcup _{l\leq j}C_{i_l}$
is both definably connected and connected. Set
$\bigcup _{l\leq j}C_{i_l}$
is both definably connected and connected. Set
![]() $i_1=1$
, and if
$i_1=1$
, and if
![]() $i_1, \ldots , i_q$
are given, let
$i_1, \ldots , i_q$
are given, let
![]() $i_{q+1}=\min \{i: i\notin \{i_1, \ldots , i_q\} \,\,\textrm {and}\,\, C_i\cap (\bigcup _{l\leq q}C_{i_l})\neq \emptyset \}$
. Let p be the maximal length of such a sequence. We claim that
$i_{q+1}=\min \{i: i\notin \{i_1, \ldots , i_q\} \,\,\textrm {and}\,\, C_i\cap (\bigcup _{l\leq q}C_{i_l})\neq \emptyset \}$
. Let p be the maximal length of such a sequence. We claim that
![]() $C:=\bigcup _{j=1}^pC_{i_j}$
is both a definably connected component and a connected component of
$C:=\bigcup _{j=1}^pC_{i_j}$
is both a definably connected component and a connected component of
![]() $\widehat {X}(F^{max})$
.
$\widehat {X}(F^{max})$
.
To see the claim, it is enough to show that if
![]() $Y\subseteq \widehat {X}(F^{max})$
is a definably connected (respectively, connected) subset such that
$Y\subseteq \widehat {X}(F^{max})$
is a definably connected (respectively, connected) subset such that
![]() $Y\cap C\neq \emptyset $
, then
$Y\cap C\neq \emptyset $
, then
![]() $Y\subseteq C$
. Indeed, if this holds, taking Y a definably connected (respectively, connected) open neighbourhood of a point of C (respectively, a point of the complement of C), we see that C is open (respectively, closed). Now let
$Y\subseteq C$
. Indeed, if this holds, taking Y a definably connected (respectively, connected) open neighbourhood of a point of C (respectively, a point of the complement of C), we see that C is open (respectively, closed). Now let
![]() $I=\{i:C_i\cap Y\neq \emptyset \}$
and
$I=\{i:C_i\cap Y\neq \emptyset \}$
and
![]() $C_Y=\bigcup _{i\in I} C_i$
. Since the
$C_Y=\bigcup _{i\in I} C_i$
. Since the
![]() $C_i$
s cover
$C_i$
s cover
![]() $\widehat {X}(F^{max})$
, we have
$\widehat {X}(F^{max})$
, we have
![]() $Y\subseteq C_Y$
. So
$Y\subseteq C_Y$
. So
![]() $C_Y$
is definably connected (respectively, connected), being of the form
$C_Y$
is definably connected (respectively, connected), being of the form
![]() $Y\cup \bigcup _{i\in I}C_i$
. Since
$Y\cup \bigcup _{i\in I}C_i$
. Since
![]() $\emptyset \neq C\cap Y\subseteq C\cap C_Y$
, it follows that
$\emptyset \neq C\cap Y\subseteq C\cap C_Y$
, it follows that
![]() $C\cup C_Y$
is definably connected (respectively, connected). By maximality of C, we have
$C\cup C_Y$
is definably connected (respectively, connected). By maximality of C, we have
![]() $C\cup C_Y=C$
, so
$C\cup C_Y=C$
, so
![]() $Y\subseteq C$
as required.
$Y\subseteq C$
as required.
The last statement of the Proposition follows from Fact 7.2.
Remark 7.5. In general, the connectedness of
![]() $B_{\mathbf {F}}(X)$
does not imply that
$B_{\mathbf {F}}(X)$
does not imply that
![]() $\widehat {X}(F^{max})$
is connected. Take F to be
$\widehat {X}(F^{max})$
is connected. Take F to be
![]() $\mathbb {R}$
with the trivial valuation, and let X be defined by
$\mathbb {R}$
with the trivial valuation, and let X be defined by
![]() $x^2+x+1$
. The space
$x^2+x+1$
. The space
![]() $B_{\mathbf {F}}(X)$
is connected, consisting of a single point that corresponds to the Galois orbit of the two 3rd roots of unity. In contrast,
$B_{\mathbf {F}}(X)$
is connected, consisting of a single point that corresponds to the Galois orbit of the two 3rd roots of unity. In contrast,
![]() $\widehat {X}(F^{max})$
consists of two isolated points and is therefore not connected.
$\widehat {X}(F^{max})$
consists of two isolated points and is therefore not connected.
As an application, we recover a result of Ducros [Reference Ducros20] about the number of connected components of semi-algebraic subsets of
![]() $V^{\mathrm {an}}$
. Let
$V^{\mathrm {an}}$
. Let
![]() $\rho $
denote the homeomorphism from
$\rho $
denote the homeomorphism from
![]() $B_{\mathbf F}(V)$
to
$B_{\mathbf F}(V)$
to
![]() $V^{\mathrm {an}}$
.
$V^{\mathrm {an}}$
.
Theorem 7.6 (Ducros [Reference Ducros20]).
Suppose F is complete. Let V be a variety over F, and let Y be a semi-algebraic subset of
![]() $V^{\mathrm {an}}$
. Then Y has finitely many connected components.
$V^{\mathrm {an}}$
. Then Y has finitely many connected components.
Proof. Since Y is a semi-algebraic subset of
![]() $V^{\mathrm {an}}$
, there is an
$V^{\mathrm {an}}$
, there is an
![]() ${\mathbf F}$
-definable subset X of V such that
${\mathbf F}$
-definable subset X of V such that
![]() $Y=\rho (B_{\mathbf F}(X))$
. By Lemma 5.21, Proposition 7.4 and Fact 7.2,
$Y=\rho (B_{\mathbf F}(X))$
. By Lemma 5.21, Proposition 7.4 and Fact 7.2,
![]() $\widehat {X}(F^{max})$
has finitely many connected components. Now the image under
$\widehat {X}(F^{max})$
has finitely many connected components. Now the image under
![]() $\pi $
(as defined in Fact 7.2) of a connected component of
$\pi $
(as defined in Fact 7.2) of a connected component of
![]() $\widehat {X}(F^{max})$
lies in a connected component of
$\widehat {X}(F^{max})$
lies in a connected component of
![]() $B_{\mathbf F}(X)$
. Since
$B_{\mathbf F}(X)$
. Since
![]() $\pi $
is surjective, this shows the result.
$\pi $
is surjective, this shows the result.
Also note that if F is algebraically closed, then each connected component of Y is also a semi-algebraically connected component. Indeed, by Lemmas 5.19 and 5.21,
![]() $\widehat {X}(F^{max})$
has finitely many definably connected components, each of which is of the form
$\widehat {X}(F^{max})$
has finitely many definably connected components, each of which is of the form
![]() $\widehat {U_i}(F^{max})$
for some
$\widehat {U_i}(F^{max})$
for some
![]() $\mathrm {v\!+\!g}$
-clopen subsets
$\mathrm {v\!+\!g}$
-clopen subsets
![]() $U_i$
(
$U_i$
(
![]() $i=1,\ldots , k$
) of X. By Proposition 7.4, each
$i=1,\ldots , k$
) of X. By Proposition 7.4, each
![]() $\widehat {U_i}(F^{max})$
is also a connected component of
$\widehat {U_i}(F^{max})$
is also a connected component of
![]() $\widehat {X}(F^{max})$
. Since
$\widehat {X}(F^{max})$
. Since
![]() $\pi :\widehat {X}(F^{max})\to B_F(X)$
(as defined in Fact 7.2) is continuous, surjective and closed and
$\pi :\widehat {X}(F^{max})\to B_F(X)$
(as defined in Fact 7.2) is continuous, surjective and closed and
![]() $\pi (\widehat {U_i}(F^{max}))=B_F(U_i)$
, each
$\pi (\widehat {U_i}(F^{max}))=B_F(U_i)$
, each
![]() $B_F(U_i)$
is a closed connected subset of
$B_F(U_i)$
is a closed connected subset of
![]() $B_F(X)$
. Let
$B_F(X)$
. Let
![]() $I_1,\ldots , I_q$
be a finite partition of
$I_1,\ldots , I_q$
be a finite partition of
![]() $\{1,\ldots , k\}$
such that for each
$\{1,\ldots , k\}$
such that for each
![]() $j\leq q$
,
$j\leq q$
,
![]() $\bigcup _{l\in I_j}B_F(U_l)$
is connected and
$\bigcup _{l\in I_j}B_F(U_l)$
is connected and
![]() $I_j$
is maximal with this property. Then as in the last part of the proof of Proposition 7.4, each
$I_j$
is maximal with this property. Then as in the last part of the proof of Proposition 7.4, each
![]() $\bigcup _{l\in I_j}B_F(U_l)=B_F(\bigcup _{l\in I_j}U_l)$
is a connected component of
$\bigcup _{l\in I_j}B_F(U_l)=B_F(\bigcup _{l\in I_j}U_l)$
is a connected component of
![]() $\widehat {X}(F^{max})$
with
$\widehat {X}(F^{max})$
with
![]() $V_j=\bigcup _{l\in I_j}U_l$
a
$V_j=\bigcup _{l\in I_j}U_l$
a
![]() $\mathrm {v\!+\!g}$
-clopen subset of X. Since F is a model of ACVF, by Remark 7.3, each
$\mathrm {v\!+\!g}$
-clopen subset of X. Since F is a model of ACVF, by Remark 7.3, each
![]() $V_j$
is
$V_j$
is
![]() ${\mathbf F}$
-definable.
${\mathbf F}$
-definable.
Fact 7.7 ([Reference Hrushovski and Loeser35, Proposition 14.1.2]).
Let X be an
![]() ${\mathbf F}$
-definable subset of an algebraic variety V over F. Then the following are equivalent:
${\mathbf F}$
-definable subset of an algebraic variety V over F. Then the following are equivalent:
-
•
 $\widehat {X}$
is definably compact.
$\widehat {X}$
is definably compact. -
•
 $\widehat {X}(F^{max})$
is compact.
$\widehat {X}(F^{max})$
is compact. -
•
 $B_{{\mathbf F}}(X)$
is compact.
$B_{{\mathbf F}}(X)$
is compact.
In particular, when F is complete,
![]() $\widehat {V}$
is definably compact if and only if
$\widehat {V}$
is definably compact if and only if
![]() $V^{\mathrm {an}}$
is compact.
$V^{\mathrm {an}}$
is compact.
![]() $\Box $
$\Box $
The proof of the previous fact in [Reference Hrushovski and Loeser35] does not seem to include the proof that
![]() $B_{\mathbf {{F}}}(X)$
is Hausdorff. For the reader’s convenience, we include an argument.
$B_{\mathbf {{F}}}(X)$
is Hausdorff. For the reader’s convenience, we include an argument.
Lemma 7.8. Let X be an
![]() ${\mathbf F}$
-definable subset of an algebraic variety V over F. Then
${\mathbf F}$
-definable subset of an algebraic variety V over F. Then
![]() $B_{\mathbf F}(X)$
is a Hausdorff topological space.
$B_{\mathbf F}(X)$
is a Hausdorff topological space.
Proof. Note that it suffices to show that when
![]() $X=V$
is a complete variety over F,
$X=V$
is a complete variety over F,
![]() $B_{\mathbf F}(V)$
is Hausdorff. Indeed, by Nagata’s theorem, there is an open immersion
$B_{\mathbf F}(V)$
is Hausdorff. Indeed, by Nagata’s theorem, there is an open immersion
![]() $V\to V'$
, where
$V\to V'$
, where
![]() $V'$
is a complete variety. Since
$V'$
is a complete variety. Since
![]() $B_{\mathbf F}(X)$
is a subspace of
$B_{\mathbf F}(X)$
is a subspace of
![]() $B_{\mathbf F}(V')$
, it is also Hausdorff.
$B_{\mathbf F}(V')$
, it is also Hausdorff.
We first show that points in
![]() $B_{\mathbf F}(V)$
are closed. Note that for each affine open subset
$B_{\mathbf F}(V)$
are closed. Note that for each affine open subset
![]() $W\subseteq V$
,
$W\subseteq V$
,
![]() $B_{\mathbf F}(W)$
is an open subspace of
$B_{\mathbf F}(W)$
is an open subspace of
![]() $B_{\mathbf F}(V)$
. Hence it suffices to show that points in
$B_{\mathbf F}(V)$
. Hence it suffices to show that points in
![]() $B_{\mathbf F}(W)$
are closed for affine W. Actually, this is true since
$B_{\mathbf F}(W)$
are closed for affine W. Actually, this is true since
![]() $B_{\mathbf F}(W)$
is even Hausdorff. Let
$B_{\mathbf F}(W)$
is even Hausdorff. Let
![]() $p,q$
be two distinct points in
$p,q$
be two distinct points in
![]() $B_{\mathbf F}(W)$
: by quantifier elimination in ACVF, there is a regular function f on W such that
$B_{\mathbf F}(W)$
: by quantifier elimination in ACVF, there is a regular function f on W such that
![]() $\mathrm {val} \circ f_*(p)=r_1\neq \mathrm {val} \circ f_*(q)=r_2$
for some
$\mathrm {val} \circ f_*(p)=r_1\neq \mathrm {val} \circ f_*(q)=r_2$
for some
![]() $r_1,r_2 \in \mathbb {R}_{\infty }$
. Then take two disjoint open subsets
$r_1,r_2 \in \mathbb {R}_{\infty }$
. Then take two disjoint open subsets
![]() $r_1\in U_1$
and
$r_1\in U_1$
and
![]() $r_2\in U_2$
. Their inverse image under
$r_2\in U_2$
. Their inverse image under
![]() $\mathrm {val} \circ f$
will be two disjoint opens in
$\mathrm {val} \circ f$
will be two disjoint opens in
![]() $B_{\mathbf F}(W)$
separating
$B_{\mathbf F}(W)$
separating
![]() $p,q$
.
$p,q$
.
Suppose now that V is a complete variety. By Remark 5.23,
![]() $\widehat {V}$
is definably compact (and Hausdorff by [Reference Hrushovski and Loeser35, Proposition 3.7.8]) so, by Fact 7.7,
$\widehat {V}$
is definably compact (and Hausdorff by [Reference Hrushovski and Loeser35, Proposition 3.7.8]) so, by Fact 7.7,
![]() $B_F(V)$
is quasi-compact. Consider the restriction map
$B_F(V)$
is quasi-compact. Consider the restriction map
![]() $\pi :\widehat {V}(F^{max})\to B_{\mathbf F}(V)$
; note that the map is closed. On the other hand, given
$\pi :\widehat {V}(F^{max})\to B_{\mathbf F}(V)$
; note that the map is closed. On the other hand, given
![]() $p_1,p_2 \in B_{\mathbf F}(V)$
, the fibres
$p_1,p_2 \in B_{\mathbf F}(V)$
, the fibres
![]() $\pi ^{-1}(p_1), \pi ^{-1}(p_2)$
are two disjoint compact subsets of
$\pi ^{-1}(p_1), \pi ^{-1}(p_2)$
are two disjoint compact subsets of
![]() $\widehat {V}(F^{max})$
and hence can be separated by open subsets
$\widehat {V}(F^{max})$
and hence can be separated by open subsets
![]() $U_1$
and
$U_1$
and
![]() $U_2$
; then
$U_2$
; then
![]() $p_1\in B_{\mathbf F}(V)\backslash \pi (\widehat {V}(F^{max})\backslash U_1)$
and
$p_1\in B_{\mathbf F}(V)\backslash \pi (\widehat {V}(F^{max})\backslash U_1)$
and
![]() $p_2 \in B_{\mathbf F}(V)\backslash \pi (\widehat {V}(F^{max})\backslash U_2)$
are two disjoint open subsets of
$p_2 \in B_{\mathbf F}(V)\backslash \pi (\widehat {V}(F^{max})\backslash U_2)$
are two disjoint open subsets of
![]() $B_{\mathbf F}(V)$
by the fact that
$B_{\mathbf F}(V)$
by the fact that
![]() $\pi $
is closed.
$\pi $
is closed.
Recall that in general,
![]() $\widehat {X}$
may fail to be a locally compact space (Remark 5.12). However, since
$\widehat {X}$
may fail to be a locally compact space (Remark 5.12). However, since
![]() $F^{max}=(F^{max})^{max}$
, by Fact 7.2,
$F^{max}=(F^{max})^{max}$
, by Fact 7.2,
![]() $\widehat {X}(F^{max})$
is homeomorphic to
$\widehat {X}(F^{max})$
is homeomorphic to
![]() $B_{F^{max}}(X)$
; and by the next result,
$B_{F^{max}}(X)$
; and by the next result,
![]() $\widehat {X}(F^{max})$
is a locally compact topological space when X is an
$\widehat {X}(F^{max})$
is a locally compact topological space when X is an
![]() ${\mathbf F}$
-definable
${\mathbf F}$
-definable
![]() $\mathrm {v\!+\!g}$
-locally closed subset of an algebraic variety V over F.
$\mathrm {v\!+\!g}$
-locally closed subset of an algebraic variety V over F.
Lemma 7.9. If X is an
![]() ${\mathbf F}$
-definable
${\mathbf F}$
-definable
![]() $\mathrm {v\!+\!g}$
-locally closed subset of an algebraic variety V over F, then
$\mathrm {v\!+\!g}$
-locally closed subset of an algebraic variety V over F, then
![]() $B_{\mathbf F}(X)$
is a locally closed subset of
$B_{\mathbf F}(X)$
is a locally closed subset of
![]() $B_{\mathbf F}(V)$
. In particular,
$B_{\mathbf F}(V)$
. In particular,
![]() $B_{\mathbf F}(X)$
is a locally compact topological space.
$B_{\mathbf F}(X)$
is a locally compact topological space.
Proof. Let U be an
![]() ${\mathbf F}$
-definable
${\mathbf F}$
-definable
![]() $\mathrm {v\!+\!g}$
-open subset of V, and let Y be an
$\mathrm {v\!+\!g}$
-open subset of V, and let Y be an
![]() ${\mathbf F}$
-definable
${\mathbf F}$
-definable
![]() $\mathrm {v\!+\!g}$
-closed subset of V such that
$\mathrm {v\!+\!g}$
-closed subset of V such that
![]() $X=Y\cap U$
. Then
$X=Y\cap U$
. Then
![]() $\widehat {Y}(F^{max})$
is a closed subset of
$\widehat {Y}(F^{max})$
is a closed subset of
![]() $\widehat {V}(F^{max})$
. By Fact 7.2,
$\widehat {V}(F^{max})$
. By Fact 7.2,
![]() $\pi (\widehat {Y}(F^{max}))=B_{\mathbf F}(Y)$
, and
$\pi (\widehat {Y}(F^{max}))=B_{\mathbf F}(Y)$
, and
![]() $B_{{\mathbf F}}(Y)$
is a closed subset of
$B_{{\mathbf F}}(Y)$
is a closed subset of
![]() $B_{\mathbf F}(V)$
since
$B_{\mathbf F}(V)$
since
![]() $\pi $
is a closed map.
$\pi $
is a closed map.
On the other hand, since
![]() $V\setminus U$
is an
$V\setminus U$
is an
![]() ${\mathbf F}$
-definable
${\mathbf F}$
-definable
![]() $\mathrm {v\!+\!g}$
-closed subset of V, by the above and the fact that
$\mathrm {v\!+\!g}$
-closed subset of V, by the above and the fact that
![]() $B_{\mathbf F}(V)\setminus B_{\mathbf F}(U)=B_{\mathbf F}(V\setminus U)$
,
$B_{\mathbf F}(V)\setminus B_{\mathbf F}(U)=B_{\mathbf F}(V\setminus U)$
,
![]() $B_{\mathbf F}(U)$
is an open subset of
$B_{\mathbf F}(U)$
is an open subset of
![]() $B_{\mathbf F}(V).$
Therefore,
$B_{\mathbf F}(V).$
Therefore,
![]() $B_{\mathbf F}(X)=B_{\mathbf F}(U)\cap B_{\mathbf F}(Y)$
is a locally closed subset of
$B_{\mathbf F}(X)=B_{\mathbf F}(U)\cap B_{\mathbf F}(Y)$
is a locally closed subset of
![]() $B_{\mathbf F}(V)$
.
$B_{\mathbf F}(V)$
.
By Nagata’s theorem, there is an open immersion
![]() $V\to V'$
, where
$V\to V'$
, where
![]() $V'$
is a complete variety (over F). Since
$V'$
is a complete variety (over F). Since
![]() $V'$
is complete,
$V'$
is complete,
![]() $\widehat {V'}$
is definably compact (Remark 5.23), so, by Fact 7.7,
$\widehat {V'}$
is definably compact (Remark 5.23), so, by Fact 7.7,
![]() $B_{\mathbf F}(V')$
is compact. Thus the result follows since (the homeomorphic image of)
$B_{\mathbf F}(V')$
is compact. Thus the result follows since (the homeomorphic image of)
![]() $B_{\mathbf F}(X)$
is also locally closed in
$B_{\mathbf F}(X)$
is also locally closed in
![]() $B_{\mathbf F}(V')$
.
$B_{\mathbf F}(V')$
.
Remark 7.10. Let V be an algebraic variety over F. Then
![]() $B_{\mathbf F}(V)$
is paracompact. Since V is a scheme of finite type, we may assume V is affine. Furthermore, since
$B_{\mathbf F}(V)$
is paracompact. Since V is a scheme of finite type, we may assume V is affine. Furthermore, since
![]() $B_{\mathbf F}(V)$
is locally compact by Lemma 7.9, it suffices to say it is
$B_{\mathbf F}(V)$
is locally compact by Lemma 7.9, it suffices to say it is
![]() $\sigma $
-compact (see [Reference Bredon14, Page 21]). Now
$\sigma $
-compact (see [Reference Bredon14, Page 21]). Now
![]() $B_{\mathbf F}(V)$
is covered by the sets
$B_{\mathbf F}(V)$
is covered by the sets
![]() $B_{\mathbf F}(X)\subseteq U$
, where X is a closed ball with radius in
$B_{\mathbf F}(X)\subseteq U$
, where X is a closed ball with radius in
![]() $\mathbb {Q}$
. Each such set is compact by Fact 7.7.
$\mathbb {Q}$
. Each such set is compact by Fact 7.7.
Fact 7.11. Let V be a quasi-projective variety over F and X an
![]() ${\mathbf F}$
-definable subset. Then there is a strong deformation retraction
${\mathbf F}$
-definable subset. Then there is a strong deformation retraction
![]() ${\mathbf I}\times B_{\mathbf F}(X)\to B_{\mathbf F}(X)$
with image a subset
${\mathbf I}\times B_{\mathbf F}(X)\to B_{\mathbf F}(X)$
with image a subset
![]() $\mathbf {\mathfrak {X}}$
homeomorphic to a semi-algebraic subset
$\mathbf {\mathfrak {X}}$
homeomorphic to a semi-algebraic subset
![]() $\mathbf {\mathcal {X}}$
of some
$\mathbf {\mathcal {X}}$
of some
![]() $\mathbb {R} ^k$
. This deformation retraction is induced by a strong deformation retraction
$\mathbb {R} ^k$
. This deformation retraction is induced by a strong deformation retraction
![]() $H:I\times \widehat {X}\to \widehat {X}$
(of [Reference Hrushovski and Loeser35, Theorem 11.1.1]) in the sense that there is a commutative diagram
$H:I\times \widehat {X}\to \widehat {X}$
(of [Reference Hrushovski and Loeser35, Theorem 11.1.1]) in the sense that there is a commutative diagram

of continuous maps, where
![]() $i:I(F^{max})=\widehat {I}(F^{max})\to {\mathbf I}=I({\mathbf F})=I(\mathbb {R} _{\infty })$
is the canonical identification. See [Reference Hrushovski and Loeser35, Corollary 14.1.6, Proposition 14.1.3 and Theorem 14.2.1].
$i:I(F^{max})=\widehat {I}(F^{max})\to {\mathbf I}=I({\mathbf F})=I(\mathbb {R} _{\infty })$
is the canonical identification. See [Reference Hrushovski and Loeser35, Corollary 14.1.6, Proposition 14.1.3 and Theorem 14.2.1].
If
![]() $F\leq F"$
is a field extension, then we have a commutative diagram of strong deformation retractions
$F\leq F"$
is a field extension, then we have a commutative diagram of strong deformation retractions

where the vertical arrows are the canonical restrictions. Furthermore, there is a finite Galois extension
![]() $F\leq F'$
such that:
$F\leq F'$
such that:
-
(1) If
 $F'\leq F"$
, then the image
$F'\leq F"$
, then the image
 $\mathbf {\mathfrak {X}}"$
of
$\mathbf {\mathfrak {X}}"$
of
 ${\mathbf I}\times B_{{\mathbf F} "}(X)\to B_{{\mathbf F} "}(X)$
is homeomorphic to the image
${\mathbf I}\times B_{{\mathbf F} "}(X)\to B_{{\mathbf F} "}(X)$
is homeomorphic to the image
 $\mathbf {\mathfrak {X}}'$
of
$\mathbf {\mathfrak {X}}'$
of
 ${\mathbf I}\times B_{{\mathbf F} '}(X)\to B_{{\mathbf F} '}(X)$
.
${\mathbf I}\times B_{{\mathbf F} '}(X)\to B_{{\mathbf F} '}(X)$
. -
(2) The image
 $\mathbf {\mathfrak {X}}$
of
$\mathbf {\mathfrak {X}}$
of
 ${\mathbf I}\times B_{{\mathbf F} }(X)\to B_{{\mathbf F} }(X)$
is homeomorphic to
${\mathbf I}\times B_{{\mathbf F} }(X)\to B_{{\mathbf F} }(X)$
is homeomorphic to
 $\mathbf {\mathfrak {X}}'/\mathrm {Gal}(F'/F)$
.
$\mathbf {\mathfrak {X}}'/\mathrm {Gal}(F'/F)$
.
See [Reference Hrushovski and Loeser35, Theorem 14.2.3 and the discussion at the beginning of Section 14.2].
![]() $\Box $
$\Box $
An immediate consequence of this fact is the following results about cohomology:
Theorem 7.12. If X is an
![]() ${\mathbf F}$
-definable subset of a quasi-projective variety V over F, then:
${\mathbf F}$
-definable subset of a quasi-projective variety V over F, then:
-
(1)
 $H^p(B_{\mathbf F}(X);L_{B_{\mathbf F}(X)})$
is finitely generated for every
$H^p(B_{\mathbf F}(X);L_{B_{\mathbf F}(X)})$
is finitely generated for every
 $p\geq 0$
.
$p\geq 0$
. -
(2) There is a finite Galois extension
 $F\leq F'$
such that for every
$F\leq F'$
such that for every
 $F'\leq F"$
, we have isomorphisms
$F'\leq F"$
, we have isomorphisms  $$ \begin{align*} H^*(B_{{\mathbf F} '}(X); L_{B_{{\mathbf F} '}(X)})\simeq H^*(B_{{\mathbf F} "}(X); L_{B_{{\mathbf F} "}(X)}). \end{align*} $$
$$ \begin{align*} H^*(B_{{\mathbf F} '}(X); L_{B_{{\mathbf F} '}(X)})\simeq H^*(B_{{\mathbf F} "}(X); L_{B_{{\mathbf F} "}(X)}). \end{align*} $$
Proof. The result follows from Fact 7.11, the homotopy axiom in topology ([Reference Bredon14, Chapter II, 11.8]) and the fact that a semi-algebraic subset of
![]() $\mathbb {R} ^k$
is homeomorphic to a finite simplicial complex.
$\mathbb {R} ^k$
is homeomorphic to a finite simplicial complex.
Note that if
![]() $B_{{\mathbf F}}(X)$
is paracompact (see Remark 7.10), then these results can be extended to an arbitrary algebraic variety V over F using the topological analogue of Corollary 3.27 ([Reference Bredon14, Chapter II, 10.2]) and the corresponding Mayer-Vietoris sequence [Reference Bredon14, Chapter II, (27)] as in the proof of Theorem 6.31 and Theorem 6.32, respectively.
$B_{{\mathbf F}}(X)$
is paracompact (see Remark 7.10), then these results can be extended to an arbitrary algebraic variety V over F using the topological analogue of Corollary 3.27 ([Reference Bredon14, Chapter II, 10.2]) and the corresponding Mayer-Vietoris sequence [Reference Bredon14, Chapter II, (27)] as in the proof of Theorem 6.31 and Theorem 6.32, respectively.
Theorem 7.13. If X is an
![]() ${\mathbf F}$
-definable
${\mathbf F}$
-definable
![]() $\mathrm {v\!+\!g}$
-locally closed subset of an algebraic variety V over F, then:
$\mathrm {v\!+\!g}$
-locally closed subset of an algebraic variety V over F, then:
-
(1)
 $H^p_c(B_{\mathbf F}(X);L_{B_{\mathbf F}(X)})$
is finitely generated for every
$H^p_c(B_{\mathbf F}(X);L_{B_{\mathbf F}(X)})$
is finitely generated for every
 $p\geq 0$
.
$p\geq 0$
. -
(2) There is a finite Galois extension
 $F\leq F'$
such that for every
$F\leq F'$
such that for every
 $F'\leq F"$
, we have isomorphisms
$F'\leq F"$
, we have isomorphisms  $$ \begin{align*} H^*_c(B_{{\mathbf F} '}(X); L_{B_{{\mathbf F} '}(X)})\simeq H^*_c(B_{{\mathbf F} "}(X); L_{B_{{\mathbf F} "}(X)}). \end{align*} $$
$$ \begin{align*} H^*_c(B_{{\mathbf F} '}(X); L_{B_{{\mathbf F} '}(X)})\simeq H^*_c(B_{{\mathbf F} "}(X); L_{B_{{\mathbf F} "}(X)}). \end{align*} $$
Proof. Suppose first that V is a quasi-projective variety over F. Note that since X is an
![]() ${\mathbf F}$
-definable
${\mathbf F}$
-definable
![]() $\mathrm {v\!+\!g}$
-locally closed subset,
$\mathrm {v\!+\!g}$
-locally closed subset,
![]() $\mathbf {\mathcal {X}}$
is locally closed. The proof of this is similar to that of Lemma 6.27 using
$\mathbf {\mathcal {X}}$
is locally closed. The proof of this is similar to that of Lemma 6.27 using
![]() $B_{{\mathbf F}}(X)$
instead of
$B_{{\mathbf F}}(X)$
instead of
![]() $\widehat {X}$
and Fact 7.7 instead of [Reference Hrushovski and Loeser35, Prposition 4.2.9]. In this case, the result follows from the homotopy axiom in topology ([Reference Bredon14, Chapter II, 11.8]) and the fact that a semi-algebraic subset of
$\widehat {X}$
and Fact 7.7 instead of [Reference Hrushovski and Loeser35, Prposition 4.2.9]. In this case, the result follows from the homotopy axiom in topology ([Reference Bredon14, Chapter II, 11.8]) and the fact that a semi-algebraic subset of
![]() $\mathbb {R} ^k$
is homeomorphic to a finite simplicial complex.
$\mathbb {R} ^k$
is homeomorphic to a finite simplicial complex.
In the general case, since the family of compact supports is paracompactifying, the results are obtained using the topological analogue of Corollary 3.27 ([Reference Bredon14, Chapter II, 10.2]) and the corresponding Mayer-Vietoris sequence [Reference Bredon14, Chapter II, (27)] as in the proof of Theorem 6.31 and Theorem 6.32, respectively.
Let K be a model of ACVF extending
![]() ${\mathbf F}$
. Below, when we write
${\mathbf F}$
. Below, when we write
![]() $\widehat {X}(K)$
, we mean
$\widehat {X}(K)$
, we mean
![]() $\widehat {X}(K)$
equipped with the
$\widehat {X}(K)$
equipped with the
![]() $\widehat {\mathrm {v\!+\!g}}$
-site; and when we write
$\widehat {\mathrm {v\!+\!g}}$
-site; and when we write
![]() $\widehat {X}(K)_{\mathrm {top}}$
, we mean the underlying topological space. Observe that since we have a homeomorphism between
$\widehat {X}(K)_{\mathrm {top}}$
, we mean the underlying topological space. Observe that since we have a homeomorphism between
![]() $\widetilde {X(K)}$
and
$\widetilde {X(K)}$
and
![]() $\widetilde {\widehat {X}(K)}$
induced by the isomorphism of sites (Remark 3.8), the natural inclusion
$\widetilde {\widehat {X}(K)}$
induced by the isomorphism of sites (Remark 3.8), the natural inclusion
![]() $\widehat {X}(K)\to \widetilde {X(K)}$
induces a natural inclusion
$\widehat {X}(K)\to \widetilde {X(K)}$
induces a natural inclusion
![]() $i:\widehat {X}(K)\to \widetilde {\widehat {X}(K)}$
and
$i:\widehat {X}(K)\to \widetilde {\widehat {X}(K)}$
and
![]() $\widehat {X}(K)$
with the induced topology is
$\widehat {X}(K)$
with the induced topology is
![]() $\widehat {X}(K)_{\mathrm {top}}$
.
$\widehat {X}(K)_{\mathrm {top}}$
.
Given
![]() ${\mathcal {F}} \in \mathrm {Mod}(A_{\widehat {X}(K)_{\widehat {\mathrm {v\!+\!g}}}})$
, we let
${\mathcal {F}} \in \mathrm {Mod}(A_{\widehat {X}(K)_{\widehat {\mathrm {v\!+\!g}}}})$
, we let
![]() ${\mathcal {F}} _{\mathrm {top}}\in \mathrm {Mod}(A_{\widehat {X}(K)_{\mathrm {top}}})$
be the sheaf induced by the natural morphism of sites
${\mathcal {F}} _{\mathrm {top}}\in \mathrm {Mod}(A_{\widehat {X}(K)_{\mathrm {top}}})$
be the sheaf induced by the natural morphism of sites
![]() $\widehat {X}(K)_{\mathrm {top}} \to \widehat {X}(K)_{\widehat {\mathrm {v\!+\!g}}}$
. Note that this is the same as
$\widehat {X}(K)_{\mathrm {top}} \to \widehat {X}(K)_{\widehat {\mathrm {v\!+\!g}}}$
. Note that this is the same as
![]() $\widetilde {{\mathcal {F}}}_{|\widehat {X}(K)_{\mathrm {top}}}$
.
$\widetilde {{\mathcal {F}}}_{|\widehat {X}(K)_{\mathrm {top}}}$
.
As observed above, when X is an
![]() ${\mathbf F}$
-definable
${\mathbf F}$
-definable
![]() $\mathrm {v\!+\!g}$
-locally closed subset of an algebraic variety V over F, then
$\mathrm {v\!+\!g}$
-locally closed subset of an algebraic variety V over F, then
![]() $\widehat {X}(F^{max})_{\mathrm {top}}$
is a locally compact topological space. Below, we use c to denote either the family of compact supports in
$\widehat {X}(F^{max})_{\mathrm {top}}$
is a locally compact topological space. Below, we use c to denote either the family of compact supports in
![]() $\widehat {X}(K)_{\mathrm {top}}$
, as usual, or the family of definably compact supports in
$\widehat {X}(K)_{\mathrm {top}}$
, as usual, or the family of definably compact supports in
![]() $\widehat {X}(K)$
as before.
$\widehat {X}(K)$
as before.
Remark 7.14. If
![]() $D\in \widetilde {c}$
is constructible, then the following hold: (1)
$D\in \widetilde {c}$
is constructible, then the following hold: (1)
![]() $D\cap \widehat {X}(F^{max})_{\mathrm {top}}$
is a quasi-compact subset of
$D\cap \widehat {X}(F^{max})_{\mathrm {top}}$
is a quasi-compact subset of
![]() $\widetilde {\widehat {X}(F^{max})}$
; (2)
$\widetilde {\widehat {X}(F^{max})}$
; (2)
![]() $D\cap \widehat {X}(F^{max})_{\mathrm {top}}$
has a fundamental system of normal and constructible locally closed neighbourhoods in
$D\cap \widehat {X}(F^{max})_{\mathrm {top}}$
has a fundamental system of normal and constructible locally closed neighbourhoods in
![]() $\widetilde {\widehat {X}(F^{max})}$
; and (3)
$\widetilde {\widehat {X}(F^{max})}$
; and (3)
![]() $D\cap \widehat {X}(F^{max})_{\mathrm {top}}$
is a compact subset of
$D\cap \widehat {X}(F^{max})_{\mathrm {top}}$
is a compact subset of
![]() $\widehat {X}(F^{max})_{\mathrm {top}}$
.
$\widehat {X}(F^{max})_{\mathrm {top}}$
.
Indeed, there is
![]() $C\in c$
(in
$C\in c$
(in
![]() $\widehat {X}(F^{max})$
) such that
$\widehat {X}(F^{max})$
) such that
![]() $D=\widetilde {C}$
, and hence
$D=\widetilde {C}$
, and hence
![]() $D\cap \widehat {X}(F^{max})_{\mathrm {top}}=\widetilde {C}\cap X=C$
. Since C is a definably compact subset of
$D\cap \widehat {X}(F^{max})_{\mathrm {top}}=\widetilde {C}\cap X=C$
. Since C is a definably compact subset of
![]() $\widehat {X}(F^{max})$
, it is a compact subset of
$\widehat {X}(F^{max})$
, it is a compact subset of
![]() $\widehat {X}(F^{max})_{\mathrm {top}}$
(Fact 7.7). Hence C is a quasi-compact subset of
$\widehat {X}(F^{max})_{\mathrm {top}}$
(Fact 7.7). Hence C is a quasi-compact subset of
![]() $\widetilde {\widehat {X}(F^{max})}$
. Finally, since c (in
$\widetilde {\widehat {X}(F^{max})}$
. Finally, since c (in
![]() $\widehat {X}(F^{max})$
) is a definably normal family of supports on
$\widehat {X}(F^{max})$
) is a definably normal family of supports on
![]() $\widehat {X}(F^{max})$
, it follows that C has a fundamental system of normal and constructible locally closed neighbourhoods in
$\widehat {X}(F^{max})$
, it follows that C has a fundamental system of normal and constructible locally closed neighbourhoods in
![]() $\widetilde {\widehat {X}(F^{max})}$
.
$\widetilde {\widehat {X}(F^{max})}$
.
The above verifies the assumptions of Corollary 3.28 for the space
![]() $\widetilde {\widehat {X}(F^{max})}$
and the subspace
$\widetilde {\widehat {X}(F^{max})}$
and the subspace
![]() $\widehat {X}(F^{max})_{\mathrm {top}}$
. Therefore, for every
$\widehat {X}(F^{max})_{\mathrm {top}}$
. Therefore, for every
![]() ${\mathcal {F}} \in \mathrm {Mod}(A_{\widehat {X}(F^{max})_{\widehat {\mathrm {v\!+\!g}}}})$
, we have an isomorphism
${\mathcal {F}} \in \mathrm {Mod}(A_{\widehat {X}(F^{max})_{\widehat {\mathrm {v\!+\!g}}}})$
, we have an isomorphism
Also note that if X is
![]() $\mathrm {v\!+\!g}$
-normal, then considering the family of
$\mathrm {v\!+\!g}$
-normal, then considering the family of
![]() $\mathrm {v\!+\!g}$
-supports given by the
$\mathrm {v\!+\!g}$
-supports given by the
![]() $\mathrm {v\!+\!g}$
-closed subsets, we get a family of
$\mathrm {v\!+\!g}$
-closed subsets, we get a family of
![]() $\mathrm {v\!+\!g}$
-normal supports on X, and, as above, we verify the assumptions of Corollary 3.28 for the space
$\mathrm {v\!+\!g}$
-normal supports on X, and, as above, we verify the assumptions of Corollary 3.28 for the space
![]() $\widetilde {\widehat {X}(F^{max})}$
and the subspace
$\widetilde {\widehat {X}(F^{max})}$
and the subspace
![]() $\widehat {X}(F^{max})_{\mathrm {top}}$
. Hence for every
$\widehat {X}(F^{max})_{\mathrm {top}}$
. Hence for every
![]() ${\mathcal {F}} \in \mathrm {Mod}(A_{\widehat {X}(F^{max})_{\widehat {\mathrm {v\!+\!g}}}})$
, we have an isomorphism
${\mathcal {F}} \in \mathrm {Mod}(A_{\widehat {X}(F^{max})_{\widehat {\mathrm {v\!+\!g}}}})$
, we have an isomorphism
In the o-minimal context,
![]() $\mathbb {R}$
plays the analogous role of
$\mathbb {R}$
plays the analogous role of
![]() $F^{max}$
in Remark 7.14, and in a similar way, we have:
$F^{max}$
in Remark 7.14, and in a similar way, we have:
Remark 7.15. Let
![]() ${\mathbf {\Gamma }}=(\mathbb {R}, < , +, \ldots )$
be an o-minimal expansion of
${\mathbf {\Gamma }}=(\mathbb {R}, < , +, \ldots )$
be an o-minimal expansion of
![]() $(\mathbb {R}, <, + )$
, and let
$(\mathbb {R}, <, + )$
, and let
![]() $X\subseteq \mathbb {R}^m_{\infty }$
be a definably locally closed subset. Let
$X\subseteq \mathbb {R}^m_{\infty }$
be a definably locally closed subset. Let
![]() $X_{\mathrm {top}}$
be X equipped with the topology generated by the open definable subsets. Then
$X_{\mathrm {top}}$
be X equipped with the topology generated by the open definable subsets. Then
![]() $X_{\mathrm {top}}$
is a locally closed subset, in particular a locally compact topological space. Also note that if we consider the natural inclusion
$X_{\mathrm {top}}$
is a locally closed subset, in particular a locally compact topological space. Also note that if we consider the natural inclusion
![]() $i:X\to \widetilde {X}$
, where
$i:X\to \widetilde {X}$
, where
![]() $\widetilde {X}=\widetilde {X}_{\mathrm {def}}$
is the o-minimal spectrum of X, then X with the induced topology is
$\widetilde {X}=\widetilde {X}_{\mathrm {def}}$
is the o-minimal spectrum of X, then X with the induced topology is
![]() $X_{\mathrm {top}}$
.
$X_{\mathrm {top}}$
.
Given
![]() ${\mathcal {F}} \in \mathrm {Mod}(A_{X_{\mathrm {def}}})$
, let
${\mathcal {F}} \in \mathrm {Mod}(A_{X_{\mathrm {def}}})$
, let
![]() ${\mathcal {F}} _{\mathrm {top}}\in \mathrm {Mod}(A_{X_{\mathrm {top}}})$
denote the sheaf induced by the natural morphism of sites
${\mathcal {F}} _{\mathrm {top}}\in \mathrm {Mod}(A_{X_{\mathrm {top}}})$
denote the sheaf induced by the natural morphism of sites
![]() $X_{\mathrm {top}} \to X_{\mathrm {def}}$
. Note that this is the same as
$X_{\mathrm {top}} \to X_{\mathrm {def}}$
. Note that this is the same as
![]() $\widetilde {{\mathcal {F}}}_{|X_{\mathrm {top}}}$
. Also let c denote either the family of compact supports on
$\widetilde {{\mathcal {F}}}_{|X_{\mathrm {top}}}$
. Also let c denote either the family of compact supports on
![]() $X_{\mathrm {top}}$
, as usual, or the family of definably compact supports on X as before. Using Remark 4.11 instead of Fact 7.7, we verify the assumptions of Corollary 3.28 for
$X_{\mathrm {top}}$
, as usual, or the family of definably compact supports on X as before. Using Remark 4.11 instead of Fact 7.7, we verify the assumptions of Corollary 3.28 for
![]() $\widetilde {X}$
and the subspace
$\widetilde {X}$
and the subspace
![]() $X_{\mathrm {top}}$
exactly in the same way as in Remark 7.14. Therefore for every
$X_{\mathrm {top}}$
exactly in the same way as in Remark 7.14. Therefore for every
![]() ${\mathcal {F}}\in \mathrm {Mod}(A_{X_{\mathrm {def}}})$
, we have an isomorphism
${\mathcal {F}}\in \mathrm {Mod}(A_{X_{\mathrm {def}}})$
, we have an isomorphism
Similary, as above, if X is definably normal, then for every
![]() ${\mathcal {F}}\in \mathrm {Mod}(A_{X_{\mathrm {def}}})$
, we have an isomorphism
${\mathcal {F}}\in \mathrm {Mod}(A_{X_{\mathrm {def}}})$
, we have an isomorphism
The topological cohomology of the model-theoretic Berkovich spaces and the
![]() $\mathrm {v\!+\!g}$
-cohomology of their corresponding stable completions are related by the following results:
$\mathrm {v\!+\!g}$
-cohomology of their corresponding stable completions are related by the following results:
Theorem 7.16. Let X be an
![]() ${\mathbf F}$
-definable
${\mathbf F}$
-definable
![]() $\mathrm {v\!+\!g}$
-locally closed subset of an algebraic variety V over F, and let
$\mathrm {v\!+\!g}$
-locally closed subset of an algebraic variety V over F, and let
![]() ${\mathcal {F}}\in \mathrm {Mod}(A_{\widehat {X}(F^{max})_{\widehat {\mathrm {v\!+\!g}}}})$
. Then we have a spectral sequence
${\mathcal {F}}\in \mathrm {Mod}(A_{\widehat {X}(F^{max})_{\widehat {\mathrm {v\!+\!g}}}})$
. Then we have a spectral sequence
which, when
![]() $F=F^{max}$
, induces isomorphisms
$F=F^{max}$
, induces isomorphisms
Proof. Considering the continuous map
![]() $\pi \colon \widehat {X}(F^{max})_{\mathrm {top}} \to B_{\mathbf F}(X)$
of locally compact topological spaces (Fact 7.2 and Lemma 7.9), we have the corresponding Leray spectral sequence ([Reference Bredon14, Chapter IV, 6.1])
$\pi \colon \widehat {X}(F^{max})_{\mathrm {top}} \to B_{\mathbf F}(X)$
of locally compact topological spaces (Fact 7.2 and Lemma 7.9), we have the corresponding Leray spectral sequence ([Reference Bredon14, Chapter IV, 6.1])
and, by Remark 7.14, we have an isomorphism
On the other hand, when
![]() $F=F^{max}$
, we get isomorphisms
$F=F^{max}$
, we get isomorphisms
since
![]() $\pi $
is a homeomorphism (Fact 7.2).
$\pi $
is a homeomorphism (Fact 7.2).
Combining Theorems 7.16 and 7.13, we have:
Corollary 7.17. Let X be an
![]() ${\mathbf F}$
-definable
${\mathbf F}$
-definable
![]() $\mathrm {v\!+\!g}$
-locally closed subset of an algebraic variety V over F. Then there is a finite Galois extension
$\mathrm {v\!+\!g}$
-locally closed subset of an algebraic variety V over F. Then there is a finite Galois extension
![]() $F\leq F'$
such that we have an isomorphism
$F\leq F'$
such that we have an isomorphism
In particular, when F is complete, we have an isomorphism
Proof. By Theorem 7.13, we have
Since
![]() $F^{\prime max}=F^{max}$
and
$F^{\prime max}=F^{max}$
and
![]() $F^{max}=(F^{max})^{max}$
, by Theorem 7.18, we have
$F^{max}=(F^{max})^{max}$
, by Theorem 7.18, we have
Similarly, using the second part of Remark 7.14 and the Leray spectral sequence ([Reference Bredon14, Chapter IV, 6.1]), we have:
Theorem 7.18. Let X be an
![]() ${\mathbf F}$
-definable
${\mathbf F}$
-definable
![]() $\mathrm {v\!+\!g}$
-normal subset of an algebraic variety V over F, and let
$\mathrm {v\!+\!g}$
-normal subset of an algebraic variety V over F, and let
![]() ${\mathcal {F}}\in \mathrm {Mod}(A_{\widehat {X}(F^{max})_{\widehat {\mathrm {v\!+\!g}}}})$
. Then we have a spectral sequence
${\mathcal {F}}\in \mathrm {Mod}(A_{\widehat {X}(F^{max})_{\widehat {\mathrm {v\!+\!g}}}})$
. Then we have a spectral sequence
which, when
![]() $F=F^{max}$
, induces isomorphisms
$F=F^{max}$
, induces isomorphisms
□
Combining this with Theorem 7.12, we obtain:
Corollary 7.19. Let X be an
![]() ${\mathbf F}$
-definable
${\mathbf F}$
-definable
![]() $\mathrm {v\!+\!g}$
-normal subset of a quasi-projective variety V over F. Then there is a finite Galois extension
$\mathrm {v\!+\!g}$
-normal subset of a quasi-projective variety V over F. Then there is a finite Galois extension
![]() $F\leq F'$
such that we have an isomorphism
$F\leq F'$
such that we have an isomorphism
In particular, when F is complete, we have an isomorphism
□
We conclude the paper with a couple of remarks.
Let X be an
![]() ${\mathbf F}$
-definable subset of an algebraic variety V over F. If
${\mathbf F}$
-definable subset of an algebraic variety V over F. If
![]() $F\leq F"\leq F^{max}$
is a field extension, then the natural restriction
$F\leq F"\leq F^{max}$
is a field extension, then the natural restriction
![]() $\pi _{F",F}: B_{{\mathbf F} "}(X)\to B_{{\mathbf F}}(X)$
is a proper map. Indeed, let
$\pi _{F",F}: B_{{\mathbf F} "}(X)\to B_{{\mathbf F}}(X)$
is a proper map. Indeed, let
![]() $V'$
be a complete variety over F such that V is an open subset. Then
$V'$
be a complete variety over F such that V is an open subset. Then
![]() $\pi _{F",F}: B_{{\mathbf F} "}(V')\to B_{\mathbf F}(V')$
is proper (by Fact 7.7), and we have a commutative diagram
$\pi _{F",F}: B_{{\mathbf F} "}(V')\to B_{\mathbf F}(V')$
is proper (by Fact 7.7), and we have a commutative diagram

of surjective restrictions such that
![]() $\pi ^{-1}(B_{\mathbf F}(X))=\pi ^{-1}(B_{{\mathbf F} "}(X))=\widehat {X}(F^{max}) $
([Reference Hrushovski and Loeser35, Proposition 14.1.2]). If
$\pi ^{-1}(B_{\mathbf F}(X))=\pi ^{-1}(B_{{\mathbf F} "}(X))=\widehat {X}(F^{max}) $
([Reference Hrushovski and Loeser35, Proposition 14.1.2]). If
![]() $C\subseteq B_{{\mathbf F}}(X)$
is compact, then it is a compact subset of
$C\subseteq B_{{\mathbf F}}(X)$
is compact, then it is a compact subset of
![]() $B_{\mathbf F}(V')$
, so
$B_{\mathbf F}(V')$
, so
![]() $\pi _{F",F}^{-1}(C)$
is a compact subset of
$\pi _{F",F}^{-1}(C)$
is a compact subset of
![]() $B_{{\mathbf F} "}(V')$
and
$B_{{\mathbf F} "}(V')$
and
![]() $\pi ^{-1}(\pi _{F",F}(C))$
is a compact subset of
$\pi ^{-1}(\pi _{F",F}(C))$
is a compact subset of
![]() $\widehat {X}(F^{max})$
. Therefore,
$\widehat {X}(F^{max})$
. Therefore,
![]() $\pi (\pi ^{-1}(\pi _{F",F}^{-1}(C)))=\pi _{F",F}^{-1}(C)$
is a compact subset of
$\pi (\pi ^{-1}(\pi _{F",F}^{-1}(C)))=\pi _{F",F}^{-1}(C)$
is a compact subset of
![]() $B_{{\mathbf F} "}(X)$
since
$B_{{\mathbf F} "}(X)$
since
![]() $\pi :\widehat {X}(F^{max})\to B_{{\mathbf F} "}(X)$
is surjective. It follows that:
$\pi :\widehat {X}(F^{max})\to B_{{\mathbf F} "}(X)$
is surjective. It follows that:
Remark 7.20. If X is an
![]() ${\mathbf F}$
-definable
${\mathbf F}$
-definable
![]() $\mathrm {v\!+\!g}$
-locally closed subset of an algebraic variety V over F and
$\mathrm {v\!+\!g}$
-locally closed subset of an algebraic variety V over F and
![]() ${\mathcal {F}} \in \mathrm {Mod} (A_{B_{{\mathbf F}}(X)})$
, then we have an isomorphism
${\mathcal {F}} \in \mathrm {Mod} (A_{B_{{\mathbf F}}(X)})$
, then we have an isomorphism
where the limit is taken over all finite Galois extensions
![]() $F\leq F"$
contained in
$F\leq F"$
contained in
![]() $F^{\mathrm {alg}}$
,
$F^{\mathrm {alg}}$
,
![]() ${\mathcal {F}} _{F^{\mathrm {alg}}}=\pi _{F^{\mathrm {alg}}, F}^{-1}{\mathcal {F}}$
and
${\mathcal {F}} _{F^{\mathrm {alg}}}=\pi _{F^{\mathrm {alg}}, F}^{-1}{\mathcal {F}}$
and
![]() ${\mathcal {F}} _{F"}=\pi _{F",F}^{-1}{\mathcal {F}}$
.
${\mathcal {F}} _{F"}=\pi _{F",F}^{-1}{\mathcal {F}}$
.
Indeed, since
![]() $B_{{\mathbf F} ^{\mathrm {alg}}}(X)$
and
$B_{{\mathbf F} ^{\mathrm {alg}}}(X)$
and
![]() $\underset {F"/F}{\underleftarrow {\lim }}B_{{\mathbf F} "}(X)$
are homeomorphic, the result follows from [Reference Bredon14, Chapter II, 14.5].
$\underset {F"/F}{\underleftarrow {\lim }}B_{{\mathbf F} "}(X)$
are homeomorphic, the result follows from [Reference Bredon14, Chapter II, 14.5].
Now let
![]() $G=\mathrm {Aut}(F^{\mathrm {alg}}/F^h)$
be the absolute Galois group of the Henselisation
$G=\mathrm {Aut}(F^{\mathrm {alg}}/F^h)$
be the absolute Galois group of the Henselisation
![]() $F^h$
of F. Recall that this is the group of valued field automorphisms of
$F^h$
of F. Recall that this is the group of valued field automorphisms of
![]() $F^{\mathrm {alg}}$
over F. As observed in [Reference Hrushovski and Loeser35, page 205], G acts continuously on
$F^{\mathrm {alg}}$
over F. As observed in [Reference Hrushovski and Loeser35, page 205], G acts continuously on
![]() $B_{{\mathbf F} ^{\mathrm {alg}}}(V)$
and
$B_{{\mathbf F} ^{\mathrm {alg}}}(V)$
and
![]() $B_{\mathbf F}(V)=B_{{\mathbf F} ^{\mathrm {alg}}}(V)/G$
. Therefore, since this action leaves
$B_{\mathbf F}(V)=B_{{\mathbf F} ^{\mathrm {alg}}}(V)/G$
. Therefore, since this action leaves
![]() $B_{{\mathbf F} ^{\mathrm { alg}}}(X)$
invariant, G acts continuously on
$B_{{\mathbf F} ^{\mathrm { alg}}}(X)$
invariant, G acts continuously on
![]() $B_{{\mathbf F} ^{\mathrm {alg}}}(X)$
and
$B_{{\mathbf F} ^{\mathrm {alg}}}(X)$
and
![]() $B_{\mathbf F}(X)=B_{{\mathbf F} ^{\mathrm {alg}}}(X)/G$
.
$B_{\mathbf F}(X)=B_{{\mathbf F} ^{\mathrm {alg}}}(X)/G$
.
Since
![]() $G=\underset {F"/F^h}{\underleftarrow {\lim }}\mathrm {Gal}(F"/F^h)$
, where the limit is taken over all finite Galois extensions
$G=\underset {F"/F^h}{\underleftarrow {\lim }}\mathrm {Gal}(F"/F^h)$
, where the limit is taken over all finite Galois extensions
![]() $F^h\leq F"$
contained in
$F^h\leq F"$
contained in
![]() $F^{\mathrm {alg}}$
, then when
$F^{\mathrm {alg}}$
, then when
![]() $F=F^h$
(i.e., it is Henselian), the isomorphism of Remark 7.20 is an isomorphism of G-modules. However, unlike the étale cohomology, we do not have the Cartan-Leray spectral sequence relating the cohomologies of
$F=F^h$
(i.e., it is Henselian), the isomorphism of Remark 7.20 is an isomorphism of G-modules. However, unlike the étale cohomology, we do not have the Cartan-Leray spectral sequence relating the cohomologies of
![]() $B_{{\mathbf F}}(X)$
and
$B_{{\mathbf F}}(X)$
and
![]() $B_{{\mathbf F}^{\mathrm { alg}}}(X)$
through the absolute Galois group
$B_{{\mathbf F}^{\mathrm { alg}}}(X)$
through the absolute Galois group
![]() $G=\mathrm {Gal}(F^{\mathrm {alg}}/F^h)$
. Indeed, in this case, G does not act freely and properly on
$G=\mathrm {Gal}(F^{\mathrm {alg}}/F^h)$
. Indeed, in this case, G does not act freely and properly on
![]() $B_{{\mathbf F}^{\mathrm {alg}}}(X)$
.
$B_{{\mathbf F}^{\mathrm {alg}}}(X)$
.
Regarding the vanishing of cohomology, we have:
Remark 7.21. Let X be an
![]() ${\mathbf F}$
-definable subset of a quasi-projective variety V over F. Since the finite simplicial complex
${\mathbf F}$
-definable subset of a quasi-projective variety V over F. Since the finite simplicial complex
![]() ${\mathcal X}$
of Fact 7.11 to can be assumed to have dimension less or equal to
${\mathcal X}$
of Fact 7.11 to can be assumed to have dimension less or equal to
![]() $\dim (\overline {X}^{\mathrm {Zar}})$
, then by the homotopy axiom in topology ([Reference Bredon14, Chapter II, 11.8]), we have:
$\dim (\overline {X}^{\mathrm {Zar}})$
, then by the homotopy axiom in topology ([Reference Bredon14, Chapter II, 11.8]), we have:
and, similarly, when X is a
![]() $\mathrm {v\!+\!g}$
-locally closed subset, we have
$\mathrm {v\!+\!g}$
-locally closed subset, we have
It is worthwhile to point out that the first of these vanishing results was also observed in the paper [Reference Basu and Patel4], where it plays a crucial role.
8 Some tameness results in families
In [Reference Hrushovski and Loeser35] Hrushovski and Loeser show finiteness of homotopy (even homeomorphism) types of uniform families of (model-theoretic) Berkovich spaces (see [Reference Hrushovski and Loeser35, Theorems 14.3.1 and 14.4.4]). In higher ranks, one has to replace the topological homotopy (respectively, homeomorphism) type by the definable homotopy (respectively, homeomorphism) type. As observed by Hrushovski and Loeser at the beginning [Reference Hrushovski and Loeser35, Section 14.3], in higher ranks, we no longer have such finiteness results. In fact, one can have a uniform family of triangles in
![]() ${\Gamma } ^2$
, corresponding to skeleta of a uniform family of elliptic curves, without finitely many definable homotopy (equivalently definable homeomorphism) types.
${\Gamma } ^2$
, corresponding to skeleta of a uniform family of elliptic curves, without finitely many definable homotopy (equivalently definable homeomorphism) types.
Taking advantage of the invariance results for our cohomology theories with definably compact supports, we can prove the finiteness of cohomological complexity in uniform families. Namely:
Theorem 8.1. Let K be an algebraically closed, nontrivially valued nonarchimedean field. Let V and
![]() $V'$
be algebraic varieties over K. Let
$V'$
be algebraic varieties over K. Let
![]() $W\subseteq V'\times {\Gamma ^k_{\infty } }$
be a K-definable subset, and let
$W\subseteq V'\times {\Gamma ^k_{\infty } }$
be a K-definable subset, and let
![]() $Z\subseteq V\times W$
be a
$Z\subseteq V\times W$
be a
![]() $\mathrm {v\!+\!g}$
-locally closed K-definable subset. For
$\mathrm {v\!+\!g}$
-locally closed K-definable subset. For
![]() $w\in W$
, let
$w\in W$
, let
![]() $Z_w=\{v\in V: (v,w)\in Z\}$
. Then as w runs through W, there are finitely many possibilities for the
$Z_w=\{v\in V: (v,w)\in Z\}$
. Then as w runs through W, there are finitely many possibilities for the
![]() $\widehat {\mathrm {v\!+\!g}}$
-cohomology
$\widehat {\mathrm {v\!+\!g}}$
-cohomology
with definably compact supports.
Proof. First, notice that it is enough to prove the result assuming that V is a quasi-projective variety. In fact, in general, if V is a variety, then V is a finite union of open quasi-projective subvarieties
![]() $V_1, \ldots , V_n$
, and the result follows by induction on n using the Mayer-Vietoris sequence as in the proof of Theorem 6.31.
$V_1, \ldots , V_n$
, and the result follows by induction on n using the Mayer-Vietoris sequence as in the proof of Theorem 6.31.
By the uniform version of the main theorem of Hrushovski and Loeser ([Reference Hrushovski and Loeser35, Proposition 11.7.1]), there is a uniformly pro-definable family
![]() $H_{w}:I\times \widehat {Z_{w}}\to \widehat {Z_{w}}$
, a definable subset
$H_{w}:I\times \widehat {Z_{w}}\to \widehat {Z_{w}}$
, a definable subset
![]() ${\mathcal Z}_{w}\subseteq {\Gamma }_{\infty }^{\dim V}$
, an iso-definable subset
${\mathcal Z}_{w}\subseteq {\Gamma }_{\infty }^{\dim V}$
, an iso-definable subset
![]() ${\mathfrak Z}_{w}$
of
${\mathfrak Z}_{w}$
of
![]() $\widehat {Z}_{w}$
and
$\widehat {Z}_{w}$
and
![]() $h_{w}:{\mathfrak Z}_{w}\to {\mathcal Z}_{w}$
, pro-definable uniformly in w, such that for each w,
$h_{w}:{\mathfrak Z}_{w}\to {\mathcal Z}_{w}$
, pro-definable uniformly in w, such that for each w,
![]() $H_{w}$
is a deformation retraction of
$H_{w}$
is a deformation retraction of
![]() $\widehat {Z}_{w}$
onto
$\widehat {Z}_{w}$
onto
![]() ${\mathfrak Z}_{w}$
, and
${\mathfrak Z}_{w}$
, and
![]() $h_{w}$
is a pro-definable homeomorphism.
$h_{w}$
is a pro-definable homeomorphism.
By stable embeddedness of
![]() ${\Gamma _{\infty } }$
(see, for example, [Reference Hrushovski and Loeser35, Proposition 2.7.1]) and elimination of imaginaries in
${\Gamma _{\infty } }$
(see, for example, [Reference Hrushovski and Loeser35, Proposition 2.7.1]) and elimination of imaginaries in
![]() ${\Gamma _{\infty } }$
, there is a K-definable subset
${\Gamma _{\infty } }$
, there is a K-definable subset
![]() $D\subseteq \Gamma _{\infty }^{m'}$
(for some
$D\subseteq \Gamma _{\infty }^{m'}$
(for some
![]() $m'$
), a K-definable surjection
$m'$
), a K-definable surjection
![]() $\tau \colon W\to D$
and a K-definable family
$\tau \colon W\to D$
and a K-definable family
![]() $\mathcal {Z}^{\prime }_{\gamma }$
with
$\mathcal {Z}^{\prime }_{\gamma }$
with
![]() $\gamma $
ranging over D, such that for every
$\gamma $
ranging over D, such that for every
![]() $w\in W$
,
$w\in W$
,
Let
![]() $K'$
be a sufficiently saturated elementary extension of K such that its value group
$K'$
be a sufficiently saturated elementary extension of K such that its value group
![]() ${\Gamma }(K')$
expands to a model
${\Gamma }(K')$
expands to a model
![]() ${\mathbf {\Gamma }} "$
of real closed fields. Then we have a commutative diagram of morphisms of
${\mathbf {\Gamma }} "$
of real closed fields. Then we have a commutative diagram of morphisms of
![]() $\widehat {\mathrm {v\!+\!g}}$
-sites
$\widehat {\mathrm {v\!+\!g}}$
-sites

and

uniformly in w, with
![]() $H_{w}^{K'}$
a pro-definable deformation retraction and
$H_{w}^{K'}$
a pro-definable deformation retraction and
![]() $h_{w}^{K'}$
a pro-definable homeomorphism and where the vertical arrows are the morphisms of
$h_{w}^{K'}$
a pro-definable homeomorphism and where the vertical arrows are the morphisms of
![]() $\widehat {\mathrm {v\!+\!g}}$
-sites taking
$\widehat {\mathrm {v\!+\!g}}$
-sites taking
![]() $\widehat {U}(K)$
to
$\widehat {U}(K)$
to
![]() $\widehat {U}(K')$
.
$\widehat {U}(K')$
.
Note that since Z is
![]() $\mathrm {v\!+\!g}$
-locally closed, each
$\mathrm {v\!+\!g}$
-locally closed, each
![]() $Z_{w}$
is also a
$Z_{w}$
is also a
![]() $\mathrm {v\!+\!g}$
-locally closed subset. By Lemma 6.27, each
$\mathrm {v\!+\!g}$
-locally closed subset. By Lemma 6.27, each
![]() $\mathcal {Z}_w$
is a definably locally closed subset. It follows that we take
$\mathcal {Z}_w$
is a definably locally closed subset. It follows that we take
![]() $\widehat {\mathrm {v\!+\!g}}$
-cohomologies with definably compact supports and obtain the following commutative diagram of isomorphisms
$\widehat {\mathrm {v\!+\!g}}$
-cohomologies with definably compact supports and obtain the following commutative diagram of isomorphisms

where
![]() $\gamma =\tau (w)$
, the vertical isomorphisms are given by the invariance results (Theorems 6.32 and 6.22) and the horizontal isomorphisms are induced by the pro-definable deformation retractions (Remark 6.30).
$\gamma =\tau (w)$
, the vertical isomorphisms are given by the invariance results (Theorems 6.32 and 6.22) and the horizontal isomorphisms are induced by the pro-definable deformation retractions (Remark 6.30).
By the definable trivialisation theorem in the real closed field
![]() ${\mathbf {\Gamma }} "$
([Reference van den Dries53, Chapter 9]), there is a partition of
${\mathbf {\Gamma }} "$
([Reference van den Dries53, Chapter 9]), there is a partition of
![]() $D({\Gamma } ")$
by finitely many
$D({\Gamma } ")$
by finitely many
![]() ${\mathbf {\Gamma }}"$
-definable subsets
${\mathbf {\Gamma }}"$
-definable subsets
![]() $D_1,\ldots , D_r$
such that for every
$D_1,\ldots , D_r$
such that for every
![]() $1\leq i\leq r$
and for all
$1\leq i\leq r$
and for all
![]() $\gamma , \gamma '\in D_i$
, we have that
$\gamma , \gamma '\in D_i$
, we have that
![]() ${\mathcal Z}_{\gamma }$
is
${\mathcal Z}_{\gamma }$
is
![]() ${\mathbf {\Gamma }} "$
-definably homeomorphic to
${\mathbf {\Gamma }} "$
-definably homeomorphic to
![]() $\mathcal {Z}_{\gamma '}$
. In particular, we have
$\mathcal {Z}_{\gamma '}$
. In particular, we have
for all
![]() $\gamma , \gamma '\in D_i$
and for every
$\gamma , \gamma '\in D_i$
and for every
![]() $1\leq i\leq r$
, and the result follows.
$1\leq i\leq r$
, and the result follows.
While Theorem 8.1 above can be see as a higher-rank analogue of [Reference Hrushovski and Loeser35, Theorem 14.3.1] concerning finiteness of homotopy types in uniform families in the rank-one case, the next result is the analogue of [Reference Hrushovski and Loeser35, Theorem 14.4.4].
Corollary 8.2. Let K be an algebraically closed nontrivially valued nonarchimedean field. Let V be an algebraic variety over K. Let
![]() $X\subseteq V$
be a
$X\subseteq V$
be a
![]() $\mathrm {v\!+\!g}$
-locally closed definable subset, and let
$\mathrm {v\!+\!g}$
-locally closed definable subset, and let
![]() $G\colon X\to {\Gamma _{\infty } }$
be a K-definable map. Then there is a finite partition of
$G\colon X\to {\Gamma _{\infty } }$
be a K-definable map. Then there is a finite partition of
![]() ${\Gamma _{\infty } }$
into intervals such that the fibres of
${\Gamma _{\infty } }$
into intervals such that the fibres of
![]() $\widehat {G}: \widehat {X}\to {\Gamma _{\infty } }$
over each interval have canonically isomorphic
$\widehat {G}: \widehat {X}\to {\Gamma _{\infty } }$
over each interval have canonically isomorphic
![]() $\widehat {\mathrm {v\!+\!g}}$
-cohomology groups with definably compact supports.
$\widehat {\mathrm {v\!+\!g}}$
-cohomology groups with definably compact supports.
Proof. Let
![]() $Z\subseteq V\times {\Gamma _{\infty } }$
be the graph of
$Z\subseteq V\times {\Gamma _{\infty } }$
be the graph of
![]() $G:X\to {\Gamma _{\infty } }$
. Then for each
$G:X\to {\Gamma _{\infty } }$
. Then for each
![]() $w\in {\Gamma _{\infty } }$
, we have
$w\in {\Gamma _{\infty } }$
, we have
![]() $Z_w=G^{-1}(w)$
and
$Z_w=G^{-1}(w)$
and
![]() $\widehat {Z}_w=\widehat {G}^{-1}(w)$
. Note that the W and D of the proof of Theorem 8.1 are both equal to
$\widehat {Z}_w=\widehat {G}^{-1}(w)$
. Note that the W and D of the proof of Theorem 8.1 are both equal to
![]() ${\Gamma _{\infty } }$
here; in particular,
${\Gamma _{\infty } }$
here; in particular,
![]() $\tau $
is the identity. So that proof gives us that, by the definable trivialisation theorem in the real closed field
$\tau $
is the identity. So that proof gives us that, by the definable trivialisation theorem in the real closed field
![]() ${\Gamma } "$
([Reference van den Dries53, Chapter 9]), there is a partition of
${\Gamma } "$
([Reference van den Dries53, Chapter 9]), there is a partition of
![]() ${\Gamma }_{\infty } "$
by finitely many
${\Gamma }_{\infty } "$
by finitely many
![]() ${\mathbf {\Gamma }}"$
-definable subsets
${\mathbf {\Gamma }}"$
-definable subsets
![]() $D_1,\ldots , D_r$
such that for every
$D_1,\ldots , D_r$
such that for every
![]() $1\leq i\leq r$
and for all
$1\leq i\leq r$
and for all
![]() $\gamma , \gamma '\in D_i$
, we have that
$\gamma , \gamma '\in D_i$
, we have that
![]() ${\mathcal Z}_{\gamma }$
is
${\mathcal Z}_{\gamma }$
is
![]() ${\mathbf {\Gamma }} "$
-definably homeomorphic to
${\mathbf {\Gamma }} "$
-definably homeomorphic to
![]() $\mathcal {Z}_{\gamma '}$
. In particular, we have
$\mathcal {Z}_{\gamma '}$
. In particular, we have
for all
![]() $\gamma , \gamma '\in D_i$
and every
$\gamma , \gamma '\in D_i$
and every
![]() $1\leq i\leq r$
. Now the definable trivialisation theorem ensures that we can take the
$1\leq i\leq r$
. Now the definable trivialisation theorem ensures that we can take the
![]() $D_i$
s to be
$D_i$
s to be
![]() ${\mathbf {\Gamma }} "$
-definable with parameters in
${\mathbf {\Gamma }} "$
-definable with parameters in
![]() ${\Gamma _{\infty } }$
; hence, by o-minimality, they are intervals in
${\Gamma _{\infty } }$
; hence, by o-minimality, they are intervals in
![]() ${\Gamma }_{\infty }"$
with end points in
${\Gamma }_{\infty }"$
with end points in
![]() ${\Gamma _{\infty } }$
. To conclude, take the intervals
${\Gamma _{\infty } }$
. To conclude, take the intervals
![]() $D_1({\Gamma _{\infty } }), \ldots , D_r({\Gamma _{\infty } })$
partitioning
$D_1({\Gamma _{\infty } }), \ldots , D_r({\Gamma _{\infty } })$
partitioning
![]() ${\Gamma _{\infty } }$
.
${\Gamma _{\infty } }$
.
Given a definable set
![]() $X\subseteq V\times {\Gamma ^n_{\infty } }$
, let
$X\subseteq V\times {\Gamma ^n_{\infty } }$
, let
![]() $\pi _0^{\mathrm {def}}$
be the functor taking
$\pi _0^{\mathrm {def}}$
be the functor taking
![]() $\widehat {X}$
into its set of definably connected components. Note that by Lemma 5.21,
$\widehat {X}$
into its set of definably connected components. Note that by Lemma 5.21,
![]() $\pi _0^{\mathrm {def}}(\widehat {X})$
is a finite set. Moreover,
$\pi _0^{\mathrm {def}}(\widehat {X})$
is a finite set. Moreover,
![]() $\pi _0^{\mathrm {def}}$
is invariant under elementary extensions of K (Lemma 5.19) and in
$\pi _0^{\mathrm {def}}$
is invariant under elementary extensions of K (Lemma 5.19) and in
![]() ${\mathbf {\Gamma }_{\infty } }$
is also invariant under o-minimal expansions. Since
${\mathbf {\Gamma }_{\infty } }$
is also invariant under o-minimal expansions. Since
![]() $\pi _0^{\mathrm {def}}$
is furthermore invariant under pro-definable deformation retractions, using the same transfer arguments as above, we can prove the following higher-rank analogue of results by A. Abbes and T. Saito ([Reference Abbes and Saito1, Theorem 5.1]) and by J. Poineau ([Reference Poineau48, Théorème 2]).
$\pi _0^{\mathrm {def}}$
is furthermore invariant under pro-definable deformation retractions, using the same transfer arguments as above, we can prove the following higher-rank analogue of results by A. Abbes and T. Saito ([Reference Abbes and Saito1, Theorem 5.1]) and by J. Poineau ([Reference Poineau48, Théorème 2]).
Corollary 8.3. Let K be an algebraically closed, nontrivially valued nonarchimedean field. Let V be an algebraic variety over K. Let
![]() $X\subseteq V$
be a K-definable subset, and let
$X\subseteq V$
be a K-definable subset, and let
![]() $G\colon X\to {\Gamma _{\infty } }$
be a K-definable map. Then there is a finite partition of
$G\colon X\to {\Gamma _{\infty } }$
be a K-definable map. Then there is a finite partition of
![]() ${\Gamma _{\infty } }$
into intervals such that over each interval I, for any
${\Gamma _{\infty } }$
into intervals such that over each interval I, for any
![]() $\epsilon ', \epsilon \in I$
, we have a canonical bijection between
$\epsilon ', \epsilon \in I$
, we have a canonical bijection between
![]() $\pi _0^{\mathrm {def}}(\widehat {G}^{-1}(\epsilon '))$
and
$\pi _0^{\mathrm {def}}(\widehat {G}^{-1}(\epsilon '))$
and
![]() $\pi _0^{\mathrm {def}}(\widehat {G}^{-1}(\epsilon ))$
.
$\pi _0^{\mathrm {def}}(\widehat {G}^{-1}(\epsilon ))$
.
We end with some remarks containing open questions that will be considered in the sequel to this paper:
Remark 8.4. One can ask if there is also a higher-rank analogue of local contractability ([Reference Hrushovski and Loeser35, Theorem 14.4.1]): for example, definable local contractibility or local acyclicity with respect to
![]() $\mathrm {v\!+\!g}$
-cohomology groups. Following the proof in [Reference Hrushovski and Loeser35], this question reduces to the corresponding question in
$\mathrm {v\!+\!g}$
-cohomology groups. Following the proof in [Reference Hrushovski and Loeser35], this question reduces to the corresponding question in
![]() ${\mathbf {\Gamma }_{\infty } }$
. See [Reference Eleftheriou29] for such results in
${\mathbf {\Gamma }_{\infty } }$
. See [Reference Eleftheriou29] for such results in
![]() ${\mathbf {\Gamma }}$
.
${\mathbf {\Gamma }}$
.
Remark 8.5. An issue that was not settled here is that of finiteness and invariance for the
![]() $\widehat {\mathrm {v\!+\!g}}$
-cohomology without supports. By Remark 6.30, that reduces to knowing if we have such results for o-minimal cohomology without supports in
$\widehat {\mathrm {v\!+\!g}}$
-cohomology without supports. By Remark 6.30, that reduces to knowing if we have such results for o-minimal cohomology without supports in
![]() ${\mathbf {\Gamma }_{\infty } }$
. Such a result would also give us the finiteness of cohomological complexity as above but without supports.
${\mathbf {\Gamma }_{\infty } }$
. Such a result would also give us the finiteness of cohomological complexity as above but without supports.
Moreover, we could also obtain in higher ranks uniform sharp bounds on
![]() $\widehat {\mathrm {v\!+\!g}}$
-Betti numbers as in a result obtained by S. Basu and D. Patel ([Reference Basu and Patel4, Theorem 2]) in the case where the valued field has rank one, using the usual topological (singular) Betti numbers. Using the strategy above, such a result could be obtained by reduction of the problem to o-minimal expansions of real closed fields and then using the analogue result in that setting proved earlier by Basu ([Reference Basu3, Theorem 2.2]).
$\widehat {\mathrm {v\!+\!g}}$
-Betti numbers as in a result obtained by S. Basu and D. Patel ([Reference Basu and Patel4, Theorem 2]) in the case where the valued field has rank one, using the usual topological (singular) Betti numbers. Using the strategy above, such a result could be obtained by reduction of the problem to o-minimal expansions of real closed fields and then using the analogue result in that setting proved earlier by Basu ([Reference Basu3, Theorem 2.2]).
Acknowledgements
We wish to thank P. Eleftheriou and L. Prelli for interesting discussions on the results presented in Section 4. We would also like to thank A. Ducros, E. Hrushovski and F. Loeser for interesting discussions.
Competing Interests
The authors have no conflicts of interest to declare.
Funding statement
P. Cubides Kovacsics was partially supported by the ERC project TOSSIBERG (Grant Agreement 637027) and individual research grant Archimedische und nicht-archimedische Stratifizierungen höherer Ordnung, funded by the DFG. M. Edmundo was supported by National Funding from FCT - Fundação para a Ciência e a Tecnologia, under the projects UIDB/04561/2020 and UIDP/04561/2020. J. Ye was partially supported by NSF research grant DMS1500671 and François Loeser’s Institut Universitaire de France grant.