No CrossRef data available.
Article contents
Maranda’s theorem for pure-injective modules and duality
Published online by Cambridge University Press: 17 March 2022
Abstract
Let R be a discrete valuation domain with field of fractions Q and maximal ideal generated by 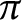 $\pi $. Let
$\pi $. Let 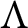 $\Lambda $ be an R-order such that
$\Lambda $ be an R-order such that 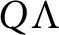 $Q\Lambda $ is a separable Q-algebra. Maranda showed that there exists
$Q\Lambda $ is a separable Q-algebra. Maranda showed that there exists 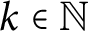 $k\in \mathbb {N}$ such that for all
$k\in \mathbb {N}$ such that for all 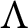 $\Lambda $-lattices L and M, if
$\Lambda $-lattices L and M, if 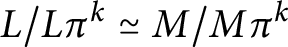 $L/L\pi ^k\simeq M/M\pi ^k$, then
$L/L\pi ^k\simeq M/M\pi ^k$, then 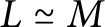 $L\simeq M$. Moreover, if R is complete and L is an indecomposable
$L\simeq M$. Moreover, if R is complete and L is an indecomposable 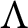 $\Lambda $-lattice, then
$\Lambda $-lattice, then 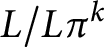 $L/L\pi ^k$ is also indecomposable. We extend Maranda’s theorem to the class of R-reduced R-torsion-free pure-injective
$L/L\pi ^k$ is also indecomposable. We extend Maranda’s theorem to the class of R-reduced R-torsion-free pure-injective 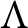 $\Lambda $-modules.
$\Lambda $-modules.
As an application of this extension, we show that if 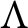 $\Lambda $ is an order over a Dedekind domain R with field of fractions Q such that
$\Lambda $ is an order over a Dedekind domain R with field of fractions Q such that 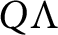 $Q\Lambda $ is separable, then the lattice of open subsets of the R-torsion-free part of the right Ziegler spectrum of
$Q\Lambda $ is separable, then the lattice of open subsets of the R-torsion-free part of the right Ziegler spectrum of 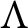 $\Lambda $ is isomorphic to the lattice of open subsets of the R-torsion-free part of the left Ziegler spectrum of
$\Lambda $ is isomorphic to the lattice of open subsets of the R-torsion-free part of the left Ziegler spectrum of 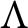 $\Lambda $.
$\Lambda $.
Furthermore, with k as in Maranda’s theorem, we show that if M is R-torsion-free and 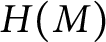 $H(M)$ is the pure-injective hull of M, then
$H(M)$ is the pure-injective hull of M, then 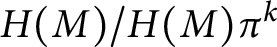 $H(M)/H(M)\pi ^k$ is the pure-injective hull of
$H(M)/H(M)\pi ^k$ is the pure-injective hull of 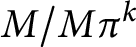 $M/M\pi ^k$. We use this result to give a characterization of R-torsion-free pure-injective
$M/M\pi ^k$. We use this result to give a characterization of R-torsion-free pure-injective 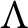 $\Lambda $-modules and describe the pure-injective hulls of certain R-torsion-free
$\Lambda $-modules and describe the pure-injective hulls of certain R-torsion-free 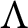 $\Lambda $-modules.
$\Lambda $-modules.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
Footnotes
The majority of this work was completed while the author was employed by the University of Camerino.


