Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-01-25T22:57:50.797Z Has data issue: false hasContentIssue false
  • English
  • Français

A FIRST-ORDER FRAMEWORK FOR INQUISITIVE MODAL LOGIC

Part of: Model theory General logic

Published online by Cambridge University Press:  31 August 2021

SILKE MEISSNER  and
MARTIN OTTO
SILKE MEISSNER
Affiliation:
DEPARTMENT FOR MATHEMATICAL LOGIC AND FOUNDATIONAL RESEARCH WESTFÄLISCHE WILHELMS-UNIVERSITÄT MÜNSTER EINSTEINSTRASSE 62, 48149MÜNSTER, GERMANYE-mail:silke.meissner@wwu.de
MARTIN OTTO
Affiliation:
DEPARTMENT OF MATHEMATICS TECHNISCHE UNIVERSITÄT DARMSTADT SCHLOSSGARTENSTRASSE 7, 64289DARMSTADT, GERMANYE-mail:otto@mathematik.tu-darmstadt.de
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a natural standard translation of inquisitive modal logic 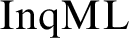$\mathrm{InqML}$ into first-order logic over the natural two-sorted relational representations of the intended models, which captures the built-in higher-order features of $\mathrm{InqML}$ . This translation is based on a graded notion of flatness that ties the inherent second-order, team-semantic features of $\mathrm{InqML}$ over information states to subsets or tuples of bounded size. A natural notion of pseudo-models, which relaxes the non-elementary constraints on the intended models, gives rise to an elementary, purely model-theoretic proof of the compactness property for $\mathrm{InqML}$ . 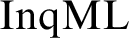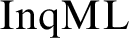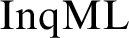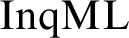Moreover, we prove a Hennessy-Milner theorem for $\mathrm{InqML}$ , which crucially uses 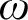$\omega $ -saturated pseudo-models and the new standard translation. As corollaries we also obtain van Benthem style characterisation theorems.

Keywords

inquisitive modal logicmodel theorystandard translationbisimulationweak models

MSC classification

Primary: 03B45: Modal logic (including the logic of norms)
Secondary: 03B42: Logics of knowledge and belief (including belief change) 03C80: Logic with extra quantifiers and operators 03C98: Applications of model theory 03B70: Logic in computer science
Type
Research Article
Information
The Review of Symbolic Logic , Volume 15 , Issue 2 , June 2022 , pp. 311 - 333
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Blackburn, P., de Rijke, M., & Venema, Y. (2001). Modal Logic. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Ciardelli, I. (2016). Questions in Logic. Ph.D. Thesis, Institute for Logic, Language and Computation.Google Scholar
Ciardelli, I., & Grilletti, G. (2017). An Ehrenfeucht–Fraïssé game for inquisitive first-order logic. In Silva, A., Staton, S., Sutton, P., and Umbach, C., editors. Twelfth International Tbilisi Symposium on Language, Logic and Computation (TbiLLC 2017). Berlin: Springer, pp. 166–186.Google Scholar
Ciardelli, I., & Otto, M. (2017). Bisimulation in inquisitive modal logic. In Lang, J., editor. Proceedings of Sixteenth Conference on Theoretical Aspects of Rationality and Knowledge (TARK’17), pp. 151–166.CrossRefGoogle Scholar
Ciardelli, I., & Otto, M. (2020). Inquisitive bisimulation. The Journal of Symbolic Logic, 86, 77–109. doi:10.1017/jsl.2020.77. Extended journal version of [4], part 1.CrossRefGoogle Scholar
Ciardelli, I., & Roelofsen, F. (2011). Inquisitive logic. Journal of Philosophical Logic, 40(1), 55–94.CrossRefGoogle Scholar
Goranko, V., & Otto, M. (2006). Model theory of modal logic. In Blackburn, P., Wolter, F., and van Benthem, J., editors. Handbook of Modal Logic. Amsterdam: Elsevier, pp. 255–325.Google Scholar
Grilletti, G. (2018). Notes on InqBQ. Private communication.Google Scholar
Grilletti, G. (2019). Disjunction and existence properties in inquisitive first-order logic. Studia Logica, 107(6), 1199–1234. doi:10.1007/s11225-018-9835-3.CrossRefGoogle Scholar
Hansen, H., Kupke, C., & Pacuit, E. (2009). Neighbourhood structures: Bisimilarity and basic model theory. Logical Methods in Computer Science, 5, 1–38.CrossRefGoogle Scholar
Hodges, W. (1993). Model Theory. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Hodges, W. (1997). Compositional semantics for a language of imperfect information. Logic Journal of the IGPL, 5, 539–563.CrossRefGoogle Scholar
Kontinen, J. (2010). Coherence and Complexity in Fragments of Dependence Logic. Ph.D. Thesis, Institute for Logic, Language and Computation.Google Scholar
Meissner, S. (2018). On the Model Theory of Inquisitive Modal Logic. Bachelor’s Thesis, Department of Mathematics, Technical University of Darmstadt.Google Scholar
Pacuit, E. (2017). Neighbourhood Semantics for Modal Logic. New York: Springer.CrossRefGoogle Scholar
Väänänen, J. (2007). Dependence Logic: A New Approach to Independence Friendly Logic. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Ziegler, M. (1985). Topological model theory. In Barwise, J., and Feferman, S., editors. Model-Theoretic Logics. New York: Springer, pp. 557–577.Google Scholar