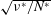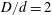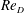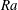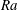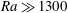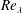Contents
JFM Papers
Velocity distributions, dispersion and stretching in three-dimensional porous media
-
- Published online by Cambridge University Press:
- 23 March 2020, A16
-
- Article
- Export citation
Shear-induced instabilities of flows through submerged vegetation
-
- Published online by Cambridge University Press:
- 23 March 2020, A17
-
- Article
- Export citation
Bidensity particle-laden exchange flows in a vertical duct
-
- Published online by Cambridge University Press:
- 23 March 2020, A18
-
- Article
- Export citation
Direct numerical simulation of turbulence in a salt-stratified fluid
-
- Published online by Cambridge University Press:
- 23 March 2020, A19
-
- Article
- Export citation
The mechanics of cilium beating: quantifying the relationship between metachronal wavelength and fluid flow rate
-
- Published online by Cambridge University Press:
- 23 March 2020, A20
-
- Article
- Export citation
Second-order curved shock theory
-
- Published online by Cambridge University Press:
- 27 March 2020, A21
-
- Article
- Export citation
Linear damped interfacial wave theory for an orbitally shaken upright circular cylinder
-
- Published online by Cambridge University Press:
- 24 March 2020, A22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Large-amplitude membrane flutter in inviscid flow
-
- Published online by Cambridge University Press:
- 26 March 2020, A23
-
- Article
- Export citation
Vortex dislocation mechanisms in the near wake of a step cylinder
-
- Published online by Cambridge University Press:
- 27 March 2020, A24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Effects of pore scale on the macroscopic properties of natural convection in porous media
-
- Published online by Cambridge University Press:
- 27 March 2020, A25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Scaling of the turbulent energy dissipation correlation function
-
- Published online by Cambridge University Press:
- 27 March 2020, A26
-
- Article
- Export citation
Viscoplastic drop impact on thin films
-
- Published online by Cambridge University Press:
- 27 March 2020, A27
-
- Article
- Export citation
Erratum
Rotating planar gravity currents at moderate Rossby numbers: fully resolved simulations and shallow-water modelling – ERRATUM
-
- Published online by Cambridge University Press:
- 18 March 2020, E1
-
- Article
-
- You have access
- HTML
- Export citation
Corrigendum
Interface-resolved simulations of small inertial particles in turbulent channel flow – CORRIGENDUM
-
- Published online by Cambridge University Press:
- 25 March 2020, E2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Front Cover (OFC, IFC) and matter
FLM volume 891 Cover and Front matter
-
- Published online by Cambridge University Press:
- 30 March 2020, p. f1
-
- Article
-
- You have access
- Export citation