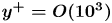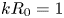Contents
JFM Papers
Mechanism of detonation stabilization in a supersonic model combustor
-
- Published online by Cambridge University Press:
- 18 January 2021, A40
-
- Article
- Export citation
Nonlinear limiting dynamics of a shrinking interface in a Hele-Shaw cell
-
- Published online by Cambridge University Press:
- 18 January 2021, A41
-
- Article
- Export citation
Turbulence in forced stratified shear flows
-
- Published online by Cambridge University Press:
- 18 January 2021, A42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analytical results for the propulsion performance of a flexible foil with prescribed pitching and heaving motions and passive small deflection
-
- Published online by Cambridge University Press:
- 18 January 2021, A43
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Capillary trapping in a vertically heterogeneous porous layer
-
- Published online by Cambridge University Press:
- 19 January 2021, A44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The late start of the mean velocity overlap log law at
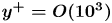 $\boldsymbol {y^+={O}(10^3)}$ – a generic feature of turbulent wall layers in ducts
$\boldsymbol {y^+={O}(10^3)}$ – a generic feature of turbulent wall layers in ducts
-
- Published online by Cambridge University Press:
- 20 January 2021, A45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rayleigh–Plateau instability of anisotropic interfaces. Part 1. An analytical and numerical study of fluid interfaces
-
- Published online by Cambridge University Press:
- 21 January 2021, A46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rayleigh–Plateau instability of anisotropic interfaces. Part 2. Limited instability of elastic interfaces
-
- Published online by Cambridge University Press:
- 22 January 2021, A47
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Scale interactions in velocity and pressure within a turbulent boundary layer developing over a staggered-cube array
-
- Published online by Cambridge University Press:
- 21 January 2021, A48
-
- Article
- Export citation
Upstream-propagating waves induced by steady current over a rippled bottom: theory and experimental observation
-
- Published online by Cambridge University Press:
- 21 January 2021, A49
-
- Article
- Export citation
Kinetic equations in a third-generation spectral wave model
-
- Published online by Cambridge University Press:
- 22 January 2021, A50
-
- Article
- Export citation
On the origins of steady streaming in precessing fluids
-
- Published online by Cambridge University Press:
- 21 January 2021, A51
-
- Article
- Export citation
Direct numerical simulation of magneto-Archimedes separation of spherical particles
-
- Published online by Cambridge University Press:
- 22 January 2021, A52
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hydrodynamic-driven morphogenesis of karst draperies: spatio-temporal analysis of the two-dimensional impulse response
-
- Published online by Cambridge University Press:
- 22 January 2021, A53
-
- Article
- Export citation
Book Review
Think Before You Compute: A Prelude to Computational Fluid Dynamics (Cambridge Texts in Applied Mathematics). By E.J. Hinch. Cambridge University Press, 2020. ISBN: 978-1-108-85529-7.
-
- Published online by Cambridge University Press:
- 13 January 2021, E1
-
- Article
- Export citation
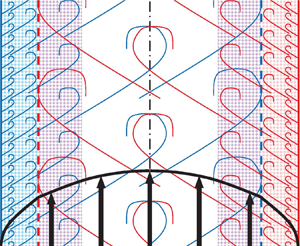
Front Cover (OFC, IFC) and matter
FLM volume 910 Cover and Front matter
-
- Published online by Cambridge University Press:
- 26 January 2021, p. f1
-
- Article
-
- You have access
- Export citation