Article contents
Mechanism of detonation stabilization in a supersonic model combustor
Published online by Cambridge University Press: 18 January 2021
Abstract
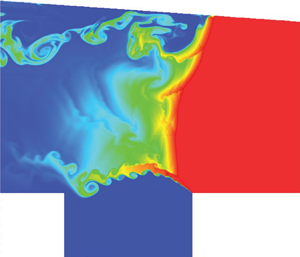
The present work studies numerically the quasi-steady propagation of a hydrogen/oxygen detonation in a supersonic model combustor consisting of a cavity and an expanding wall. The two-dimensional reactive compressible Navier–Stokes equations with a one-step and two-species reaction model are solved using a hybrid sixth-order weighted essentially non-oscillatory-centred difference scheme combined with a structured adaptive mesh refinement technique. The results show that, after the shutdown of the hot jet, the detonation wave is successfully stabilized quasi-steadily in the supersonic model combustor together with periodic fluctuations of the detonation front. The formation of the quasi-steady propagation of detonation in the model combustor is mainly due to the combined effects of (i) pressure oscillations generated in the cavity, which facilitate the detonation propagation, and (ii) lateral mass divergence brought by the expanding wall, which can lead to detonation attenuation, and an unburned jet associated with large-scale vortices resulting from a Prandtl–Meyer expansion fan. This expansion fan is generated because of the expanding wall, which can contribute to the detonation stabilization. It is found that, for an incoming velocity lower than the Chapman–Jouguet value, a quasi-steady propagation of the detonation wave cannot be achieved. However, for incoming velocity higher than the Chapman–Jouguet value, a stabilization can be realized. This is effectively due to the formation of a periodic process, including four stages of forward propagation, detonation attenuation, backward propagation and detonation bifurcation, indicating the influence of the supersonic model combustor on the overall process.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
- 10
- Cited by


