Article contents
Hydrodynamic-driven morphogenesis of karst draperies: spatio-temporal analysis of the two-dimensional impulse response
Published online by Cambridge University Press: 22 January 2021
Abstract
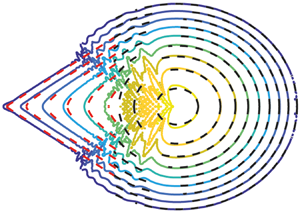
We study the role of hydrodynamic instabilities in the morphogenesis of some typical karst draperies structures encountered in limestone caves. The problem is tackled using the long wave approximation for the fluid film that flows under an inclined substrate, in the presence of substrate variations that grow according to a deposition law. We numerically study the linear and nonlinear evolution of a localized initial perturbation both in the fluid film and on the substrate, i.e. the Green function. A novel approach for the spatio-temporal analysis of two-dimensional signals resulting from linear simulations is introduced, based on the concepts of the Riesz transform and the monogenic signal, the multidimensional complex continuation of a real signal. This method allows for a deeper understanding of the pattern formation. The linear evolution of an initial localized perturbation in the presence of deposition is studied. The deposition linearly selects substrate structures aligned along the streamwise direction, as the spatio-temporal response is advected away. Furthermore, the growth of the initial defect produces a quasi-steady region also characterized by streamwise structures both on the substrate and the fluid film, which is in good agreement with the Green function for a steady defect on the substrate, in the absence of deposition.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
A correction has been issued for this article:
- 11
- Cited by
Linked content
Please note a has been issued for this article.


