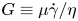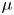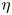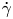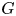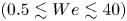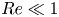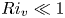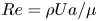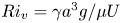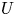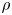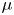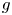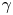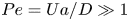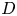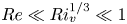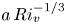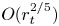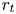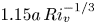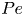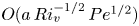Graphical abstract from L'Estimé, M., Duchemin, L., Reyssat, É. & Bico, J. 2022 Fingering instability in adhesion fronts. J. Fluid Mech. 949, A46. doi:10.1017/jfm.2022.789.
Contents
JFM Papers
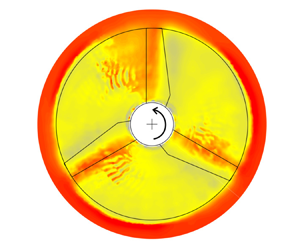
Electro-vortex flows in a cylindrical cell under axial magnetic field
-
- Published online by Cambridge University Press:
- 28 September 2022, A20
-
- Article
- Export citation
Modelling and analysis of an endothermic reacting counter-current flow
-
- Published online by Cambridge University Press:
- 29 September 2022, A21
-
- Article
- Export citation
Shape dynamics and rheology of dilute suspensions of elastic and viscoelastic particles
-
- Published online by Cambridge University Press:
- 29 September 2022, A22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bridging-droplet transfer from solid to porous surfaces
-
- Published online by Cambridge University Press:
- 29 September 2022, A23
-
- Article
- Export citation
On the relationship between turbine thrust and near-wake velocity and vorticity
-
- Published online by Cambridge University Press:
- 29 September 2022, A24
-
- Article
- Export citation
Learned turbulence modelling with differentiable fluid solvers: physics-based loss functions and optimisation horizons
-
- Published online by Cambridge University Press:
- 29 September 2022, A25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ensemble Kalman method for learning turbulence models from indirect observation data
-
- Published online by Cambridge University Press:
- 29 September 2022, A26
-
- Article
-
- You have access
- HTML
- Export citation
On the fate of a drop jumping over a gap
-
- Published online by Cambridge University Press:
- 29 September 2022, A27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The role of vibrations for reducing the resistance in the relative movement of parallel plates
-
- Published online by Cambridge University Press:
- 29 September 2022, A28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Motion of a sphere in a viscous density stratified fluid
-
- Published online by Cambridge University Press:
- 29 September 2022, A29
-
- Article
- Export citation
Scale-to-scale turbulence modification by small settling particles
-
- Published online by Cambridge University Press:
- 29 September 2022, A30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Phase-resolved ocean wave forecast with simultaneous current estimation through data assimilation
-
- Published online by Cambridge University Press:
- 30 September 2022, A31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Role of surfactant-induced Marangoni stresses in retracting liquid sheets
-
- Published online by Cambridge University Press:
- 30 September 2022, A32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Vortex structures in the wake of a marine propeller operating close to a free surface
-
- Published online by Cambridge University Press:
- 30 September 2022, A33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shear flow over a surface containing a groove covered by an incompressible surfactant phase
-
- Published online by Cambridge University Press:
- 30 September 2022, A34
-
- Article
- Export citation
Linear impulse response in three-dimensional oscillatory boundary layers formed by periodic modulation of a rotating disk
-
- Published online by Cambridge University Press:
- 30 September 2022, A35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Caustics in turbulent aerosols: an excitable system approach
-
- Published online by Cambridge University Press:
- 30 September 2022, A36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transitional hypersonic flow over slender cone/flare geometries
-
- Published online by Cambridge University Press:
- 30 September 2022, A37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Gravity-driven coatings on curved substrates: a differential geometry approach
-
- Published online by Cambridge University Press:
- 03 October 2022, A38
-
- Article
- Export citation
Flow–structure interaction of a starting jet through a flexible circular nozzle
-
- Published online by Cambridge University Press:
- 10 October 2022, A39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation