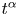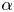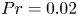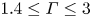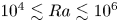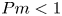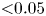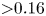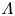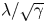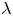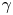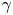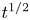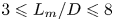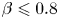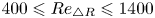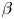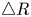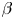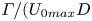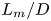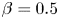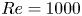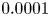Graphical abstract from L'Estimé, M., Duchemin, L., Reyssat, É. & Bico, J. 2022 Fingering instability in adhesion fronts. J. Fluid Mech. 949, A46. doi:10.1017/jfm.2022.789.
Contents
JFM Papers
Lubricated axisymmetric gravity currents of power-law fluids
-
- Published online by Cambridge University Press:
- 03 October 2022, A40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Interactions between upstream-propagating guided jet waves and shear-layer instability waves near the nozzle of subsonic and nearly ideally expanded supersonic free jets with laminar boundary layers
-
- Published online by Cambridge University Press:
- 03 October 2022, A41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Oscillations of the large-scale circulation in experimental liquid metal convection at aspect ratios 1.4–3
-
- Published online by Cambridge University Press:
- 06 October 2022, A42
-
- Article
- Export citation
Non-ideal instabilities in sinusoidal shear flows with a streamwise magnetic field
-
- Published online by Cambridge University Press:
- 06 October 2022, A43
-
- Article
- Export citation
Stability of non-isothermal Poiseuille flow in a fluid overlying an anisotropic and inhomogeneous porous domain
-
- Published online by Cambridge University Press:
- 10 October 2022, A44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Attenuation of turbulence in a periodic cube by finite-size spherical solid particles
-
- Published online by Cambridge University Press:
- 06 October 2022, A45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
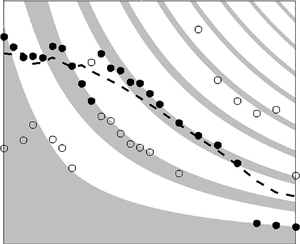
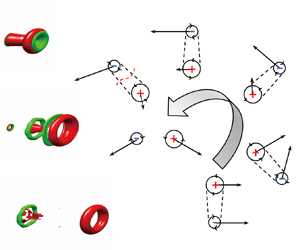
Fingering instability in adhesion fronts
-
- Published online by Cambridge University Press:
- 06 October 2022, A46
-
- Article
- Export citation
The formation process of annular starting jets
-
- Published online by Cambridge University Press:
- 06 October 2022, A47
-
- Article
- Export citation
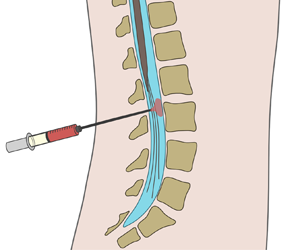
Buoyancy-modulated Lagrangian drift in wavy-walled vertical channels as a model problem to understand drug dispersion in the spinal canal
-
- Published online by Cambridge University Press:
- 06 October 2022, A48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Direct numerical simulation of elastic turbulence in the Taylor–Couette flow: transition pathway and mechanistic insight
-
- Published online by Cambridge University Press:
- 06 October 2022, A49
-
- Article
- Export citation
A Hamiltonian Dysthe equation for deep-water gravity waves with constant vorticity
-
- Published online by Cambridge University Press:
- 07 October 2022, A50
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The influence of temporal heating modulation on non-isothermal floating droplet dynamics
-
- Published online by Cambridge University Press:
- 07 October 2022, A51
-
- Article
- Export citation
Corrigendum
The inertial orientation dynamics of anisotropic particles in planar linear flows – CORRIGENDUM
-
- Published online by Cambridge University Press:
- 07 October 2022, E1
-
- Article
-
- You have access
- HTML
- Export citation
Front Cover (OFC, IFC) and matter
FLM volume 949 Cover and Front matter
-
- Published online by Cambridge University Press:
- 11 October 2022, pp. f1-f2
-
- Article
-
- You have access
- Export citation