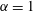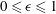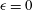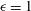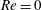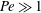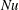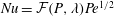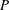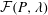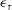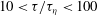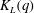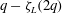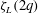Most cited
This page lists all time most cited articles for this title. Please use the publication date filters on the left if you would like to restrict this list to recently published content, for example to articles published in the last three years. The number of times each article was cited is displayed to the right of its title and can be clicked to access a list of all titles this article has been cited by.
- Cited by 10
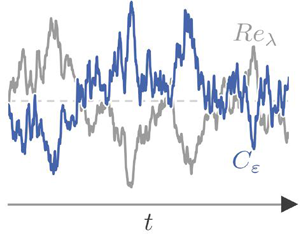
Scalings of turbulence dissipation in space and time for turbulent channel flow
-
- Published online by Cambridge University Press:
- 11 August 2022, A41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 10
The enhancement of viscous fingering with bidisperse particle suspension
-
- Published online by Cambridge University Press:
- 07 December 2018, pp. 487-509
-
- Article
- Export citation
- Cited by 10
Divergent Richtmyer–Meshkov instability on a heavy gas layer
-
- Published online by Cambridge University Press:
- 24 March 2023, A37
-
- Article
- Export citation
- Cited by 10
Binary collision dynamics of equal-sized nanodroplets
-
- Published online by Cambridge University Press:
- 11 January 2024, A25
-
- Article
- Export citation
- Cited by 10
Energy harvesting using an inverted piezohydroelastic flag with resistor–inductor–capacitor circuit
-
- Published online by Cambridge University Press:
- 28 November 2023, A49
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 10
Plunging breakers. Part 2. Droplet generation
-
- Published online by Cambridge University Press:
- 25 July 2023, A36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 10
Superconfined falling liquid films: linear versus nonlinear dynamics
-
- Published online by Cambridge University Press:
- 25 May 2021, R2
-
- Article
- Export citation
- Cited by 10
Wall-pressure fluctuations in an axisymmetric boundary layer under strong adverse pressure gradient
-
- Published online by Cambridge University Press:
- 05 April 2023, A28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
- Cited by 10
The structure of the Stewartson layers in a gas centrifuge. Part 2. Insulated side wall
-
- Published online by Cambridge University Press:
- 12 April 2006, pp. 443-457
-
- Article
- Export citation
- Cited by 10
Asymptotic solutions in non-equilibrium nozzle flow
-
- Published online by Cambridge University Press:
- 28 March 2006, pp. 243-272
-
- Article
- Export citation
- Cited by 10
Hydrodynamic stability of the boundary layer on a continuous moving surface
-
- Published online by Cambridge University Press:
- 28 March 2006, pp. 145-161
-
- Article
- Export citation
- Cited by 10
Swirling flow through a convergent funnel
-
- Published online by Cambridge University Press:
- 28 March 2006, pp. 575-593
-
- Article
- Export citation
- Cited by 10
Heat or mass transport from drops in shearing flows. Part 1. The open-streamline regime
-
- Published online by Cambridge University Press:
- 06 July 2018, pp. 439-483
-
- Article
- Export citation
- Cited by 10
Lagrangian cascade in three-dimensional homogeneous and isotropic turbulence
-
- Published online by Cambridge University Press:
- 12 February 2014, R2
-
- Article
- Export citation
- Cited by 10
Influence of pitch rate on freely translating perching airfoils
-
- Published online by Cambridge University Press:
- 20 June 2019, pp. 49-71
-
- Article
- Export citation
- Cited by 10
Two-dimensional flows with zero net momentum: evolution of vortex quadrupoles and oscillating-grid turbulence
-
- Published online by Cambridge University Press:
- 26 April 2006, pp. 21-44
-
- Article
- Export citation
- Cited by 10
Development of flow field when a symmetrical underexpanded sonic jet impinges on a flat plate
-
- Published online by Cambridge University Press:
- 20 April 2006, pp. 299-313
-
- Article
- Export citation
- Cited by 10
Chaotic mode competition in the shape oscillations of pulsating bubbles
-
- Published online by Cambridge University Press:
- 26 April 2006, pp. 257-276
-
- Article
- Export citation
- Cited by 10
Pressure-wave propagation through a separated gas-liquid layer in a duct
-
- Published online by Cambridge University Press:
- 29 March 2006, pp. 721-731
-
- Article
- Export citation
- Cited by 10
On the secondary instability in inclined air layers
-
- Published online by Cambridge University Press:
- 19 April 2006, pp. 481-492
-
- Article
- Export citation