Hostname: page-component-7dd5485656-bvgqh Total loading time: 0 Render date: 2025-10-31T03:50:18.186Z Has data issue: false hasContentIssue false
  • English
  • Français

Lagrangian cascade in three-dimensional homogeneous and isotropic turbulence

Published online by Cambridge University Press:  12 February 2014

Yongxiang Huang  and
François G. Schmitt
Yongxiang Huang*
Affiliation:
Shanghai Institute of Applied Mathematics and Mechanics, and Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai University, Shanghai 200072, PR China
François G. Schmitt
Affiliation:
Université Lille Nord de France, F-59000 Lille, France USTL, LOG, F-62930 Wimereux, France CNRS, UMR 8187, F-62930 Wimereux, France
*
†Email address for correspondence: yongxianghuang@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

In this work, the scaling statistics of the dissipation along Lagrangian trajectories are investigated by using fluid tracer particles obtained from a high-resolution direct numerical simulation with 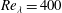$\mathit{Re}_{\lambda }=400$. Both the energy dissipation rate $\epsilon $ and the local time-averaged 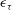$\epsilon _{\tau }$ agree rather well with the lognormal distribution hypothesis. Several statistics are then examined. It is found that the autocorrelation function 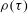$\rho (\tau )$ of 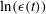$\ln (\epsilon (t))$ and variance 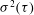$\sigma ^2(\tau )$ of 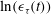$\ln (\epsilon _{\tau }(t))$ obey a log-law with scaling exponent 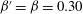$\beta '=\beta =0.30$ compatible with the intermittency parameter 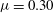$\mu =0.30$. The 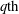$q{\rm th}$-order moment of 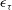$\epsilon _{\tau }$ has a clear power law on the inertial range 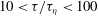$10<\tau /\tau _{\eta }<100$. The measured scaling exponent 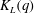$K_L(q)$ agrees remarkably with 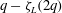$q-\zeta _L(2q)$ where 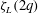$\zeta _L(2q)$ is the scaling exponent estimated using the Hilbert methodology. All of these results suggest that the dissipation along Lagrangian trajectories could be modelled by a multiplicative cascade.

JFM classification

Turbulent Flows: Homogeneous turbulence Turbulent Flows: Intermittency Turbulent Flows: Isotropic turbulence

Information

Type
Rapids
Information
Journal of Fluid Mechanics , Volume 741 , 25 February 2014 , R2
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Arneodo, A., Bacry, E., Manneville, S. & Muzy, J. F. 1998 Analysis of random cascades using space-scale correlation functions. Phys. Rev. Lett. 80 (4), 708–711.Google Scholar
Benzi, R., Biferale, L., Calzavarini, E., Lohse, D. & Toschi, F. 2009 Velocity-gradient statistics along particle trajectories in turbulent flows: the refined similarity hypothesis in the Lagrangian frame. Phys. Rev. E 80 (6), 066318.Google Scholar
Biferale, L., Boffetta, G., Celani, A., Devenish, B. J., Lanotte, A. & Toschi, F. 2004 Multifractal statistics of Lagrangian velocity and acceleration in turbulence. Phys. Rev. Lett. 93 (6), 064502.CrossRefGoogle ScholarPubMed
Borgas, M. S. 1993 The multifractal Lagrangian nature of turbulence. Phil. Trans. R. Soc. A 342 (1665), 379–411.Google Scholar
Chen, S. Y., Sreenivasan, K. R., Nelkin, M & Cao, N. Z. 1997 Refined similarity hypothesis for transverse structure functions in fluid turbulence. Phys. Rev. Lett. 79 (12), 2253–2256.Google Scholar
Chevillard, L. & Meneveau, C. 2006 Lagrangian dynamics and statistical geometric structure of turbulence. Phys. Rev. Lett. 97 (17), 174501.CrossRefGoogle ScholarPubMed
Chevillard, L., Roux, S. G., Lévêque, E., Mordant, N., Pinton, J.-F. & Arnéodo, A. 2003 Lagrangian velocity statistics in turbulent flows: effects of dissipation. Phys. Rev. Lett. 91 (21), 214502.Google Scholar
Falkovich, G., Xu, H. T., Pumir, A., Bodenschatz, E., Biferale, L., Boffetta, G., Lanotte, A. S. & Toschi, F. 2012 On Lagrangian single-particle statistics. Phys. Fluids 24 (4), 055102.Google Scholar
Frisch, U. 1995 Turbulence: The Legacy of AN Kolmogorov. Cambridge University Press.CrossRefGoogle Scholar
Homann, H., Schulz, D. L. & Grauer, R. 2011 Conditional Eulerian and Lagrangian velocity increment statistics of fully developed turbulent flow. Phys. Fluids 23, 055102.Google Scholar
Huang, Y. X., Biferale, L., Calzavarini, E., Sun, C. & Toschi, F. 2013 Lagrangian single particle turbulent statistics through the Hilbert–Huang transforms. Phys. Rev. E 87, 041003(R).Google Scholar
Huang, Y. X., Schmitt, F. G., Lu, Z. M., Fougairolles, P., Gagne, Y. & Liu, Y. L. 2010 Second-order structure function in fully developed turbulence. Phys. Rev. E 82 (2), 026319.Google Scholar
Kahane, J. P. 1985 Sur le chaos multiplicatif. Ann. Sci. Math. Que. 9 (2), 105–150.Google Scholar
Kholmyansky, M. & Tsinober, A. 2009 On an alternative explanation of anomalous scaling and how well-defined is the concept of inertial range. Phys. Lett. A 373 (27), 2364–2367.Google Scholar
Kolmogorov, A. N. 1941 Local structure of turbulence in an incompressible fluid at very high Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 301.Google Scholar
Kolmogorov, A. N. 1962 A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 13, 82–85.CrossRefGoogle Scholar
Meneveau, C. 2011 Lagrangian dynamics and models of the velocity gradient tensor in turbulent flows. Annu. Rev. Fluid Mech. 43, 219–245.Google Scholar
Mordant, N., Delour, J., Léveque, E., Arnéodo, A. & Pinton, J.-F. 2002 Long time correlations in Lagrangian dynamics: a key to intermittency in turbulence. Phys. Rev. Lett. 89 (25), 254502.Google Scholar
Pope, S. B. 1990 Lagrangian microscales in turbulence. Phil. Trans. R. Soc. A 333 (1631), 309–319.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Pope, S. B. & Chen, Y. L. 1990 The velocity-dissipation probability density function model for turbulent flows. Phys. Fluids 2, 1437–1449.Google Scholar
Praskovsky, A., Praskovskaya, E. & Horst, T. 1997 Further experimental support for the Kolmogorov refined similarity hypothesis. Phys. Fluids 9 (9), 2465–2467.Google Scholar
Sawford, B. L. & Yeung, P. K. 2011 Kolmogorov similarity scaling for one-particle Lagrangian statistics. Phys. Fluids 23, 091704.Google Scholar
Schmitt, F. G. 2003 A causal multifractal stochastic equation and its statistical properties. Eur. Phys. J. B 34 (1), 85–98.Google Scholar
Sreenivasan, K. R. & Antonia, R. A. 1997 The phenomenology of small-scale turbulence. Annu. Rev. Fluid Mech. 29, 435–472.Google Scholar
Stolovitzky, G., Kailasnath, P. & Sreenivasan, K. R. 1992 Kolmogorov’s refined similarity hypotheses. Phys. Rev. Lett. 69 (8), 1178–1181.Google Scholar
Stolovitzky, G. & Sreenivasan, K. R. 1994 Kolmogorov’s refined similarity hypotheses for turbulence and general stochastic processes. Rev. Mod. Phys. 66 (1), 229–240.Google Scholar
Toschi, F. & Bodenschatz, E. 2009 Lagrangian properties of particles in turbulence. Annu. Rev. Fluid Mech. 41, 375–404.Google Scholar
Tsinober, A. 2009 An Informal Conceptual Introduction to Turbulence. Springer.CrossRefGoogle Scholar
Xu, H. T., Bourgoin, M., Ouellette, N. T. & Bodenschatz, E. 2006a High order Lagrangian velocity statistics in turbulence. Phys. Rev. Lett. 96 (2), 024503.Google Scholar
Xu, H. T., Ouellette, N. T. & Bodenschatz, E. 2006b Multifractal dimension of Lagrangian turbulence. Phys. Rev. Lett. 96 (11), 114503.Google Scholar
Yeung, P. K. 2002 Lagrangian investigations of turbulence. Annu. Rev. Fluid Mech. 34 (1), 115–142.Google Scholar
Yu, H. D. & Meneveau, C. 2010 Lagrangian refined Kolmogorov similarity hypothesis for gradient time evolution and correlation in turbulent flows. Phys. Rev. Lett. 104 (8), 084502.Google Scholar