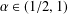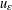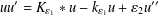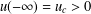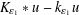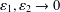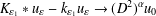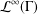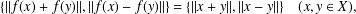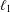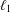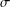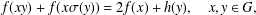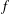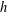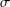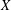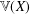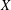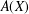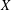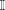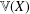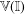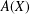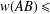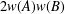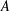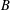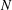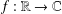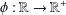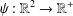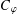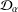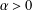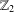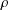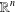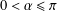Contents
Research Article
EXISTENCE OF TRAVELLING WAVES IN THE FRACTIONAL BURGERS EQUATION
- Part of:
-
- Published online by Cambridge University Press:
- 20 December 2017, pp. 102-109
-
- Article
-
- You have access
- Export citation
WIGNER’S THEOREM IN
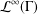 ${\mathcal{L}}^{\infty }(\unicode[STIX]{x1D6E4})$ -TYPE SPACES
${\mathcal{L}}^{\infty }(\unicode[STIX]{x1D6E4})$ -TYPE SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 04 December 2017, pp. 279-284
-
- Article
-
- You have access
- Export citation
NONEXPANSIVE BIJECTIONS TO THE UNIT BALL OF THE
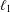 $\ell _{1}$ -SUM OF STRICTLY CONVEX BANACH SPACES
$\ell _{1}$ -SUM OF STRICTLY CONVEX BANACH SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 20 February 2018, pp. 285-292
-
- Article
-
- You have access
- Export citation
ON THE HYPERSTABILITY OF A PEXIDERISED
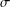 $\unicode[STIX]{x1D70E}$ -QUADRATIC FUNCTIONAL EQUATION ON SEMIGROUPS
$\unicode[STIX]{x1D70E}$ -QUADRATIC FUNCTIONAL EQUATION ON SEMIGROUPS
-
- Published online by Cambridge University Press:
- 07 March 2018, pp. 459-470
-
- Article
-
- You have access
- Export citation
SUBSPACES OF THE FREE TOPOLOGICAL VECTOR SPACE ON THE UNIT INTERVAL
- Part of:
-
- Published online by Cambridge University Press:
- 07 August 2017, pp. 110-118
-
- Article
-
- You have access
- Export citation
IMPROVED INEQUALITIES FOR THE NUMERICAL RADIUS: WHEN INVERSE COMMUTES WITH THE NORM
- Part of:
-
- Published online by Cambridge University Press:
- 02 February 2018, pp. 293-296
-
- Article
-
- You have access
- Export citation
WEAK HAAGERUP PROPERTY OF
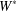 $W^{\ast }$ -CROSSED PRODUCTS
$W^{\ast }$ -CROSSED PRODUCTS
- Part of:
-
- Published online by Cambridge University Press:
- 31 August 2017, pp. 119-126
-
- Article
-
- You have access
- Export citation
STABILITY OF AN EXPONENTIAL-MONOMIAL FUNCTIONAL EQUATION
-
- Published online by Cambridge University Press:
- 28 March 2018, pp. 471-479
-
- Article
-
- You have access
- Export citation
THE HARDY AND HEISENBERG INEQUALITIES IN MORREY SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2018, pp. 480-491
-
- Article
-
- You have access
- Export citation
THE ESSENTIAL NORMS OF COMPOSITION OPERATORS ON WEIGHTED DIRICHLET SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 31 January 2018, pp. 297-307
-
- Article
-
- You have access
- Export citation
ON GRADED
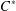 $C^{\ast }$ -ALGEBRAS
$C^{\ast }$ -ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 04 October 2017, pp. 127-132
-
- Article
-
- You have access
- Export citation
A REMARK ON THE TRACIAL ROKHLIN PROPERTY
- Part of:
-
- Published online by Cambridge University Press:
- 07 March 2018, pp. 492-498
-
- Article
-
- You have access
- Export citation
PRODUCTS OF ROTATIONS BY A GIVEN ANGLE IN THE ORTHOGONAL GROUP
- Part of:
-
- Published online by Cambridge University Press:
- 02 November 2017, pp. 308-312
-
- Article
-
- You have access
- Export citation
ALMOST INVARIANT HALF-SPACES FOR OPERATORS ON HILBERT SPACE
- Part of:
-
- Published online by Cambridge University Press:
- 31 August 2017, pp. 133-140
-
- Article
-
- You have access
- Export citation
DEFORMING A CONVEX DOMAIN INTO A DISK BY KLAIN’S CYCLIC REARRANGEMENT
- Part of:
-
- Published online by Cambridge University Press:
- 20 February 2018, pp. 313-319
-
- Article
-
- You have access
- Export citation
FRACTIONAL INTEGRAL OPERATORS ON
 $\unicode[STIX]{x1D6FC}$ -MODULATION SPACES IN THE FULL RANGE
$\unicode[STIX]{x1D6FC}$ -MODULATION SPACES IN THE FULL RANGE
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2018, pp. 499-512
-
- Article
-
- You have access
- Export citation
MAPPING PROPERTIES OF A SCALE INVARIANT CASSINIAN METRIC AND A GROMOV HYPERBOLIC METRIC
- Part of:
-
- Published online by Cambridge University Press:
- 18 August 2017, pp. 141-152
-
- Article
-
- You have access
- Export citation
LYAPUNOV EXPONENTS ON METRIC SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 04 October 2017, pp. 153-162
-
- Article
-
- You have access
- Export citation
CONTINUITY ON GENERALISED TOPOLOGICAL SPACES VIA HEREDITARY CLASSES
- Part of:
-
- Published online by Cambridge University Press:
- 21 February 2018, pp. 320-330
-
- Article
-
- You have access
- Export citation
A SIMPLE PROOF OF THE STRONG LAW OF LARGE NUMBERS WITH RATES
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2018, pp. 513-517
-
- Article
-
- You have access
- Export citation