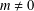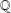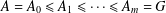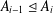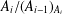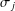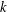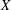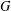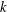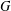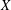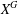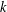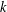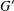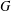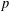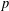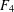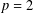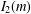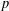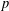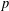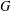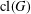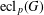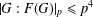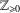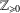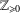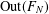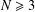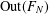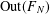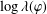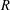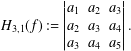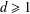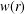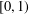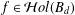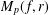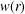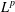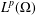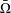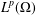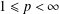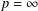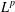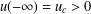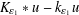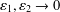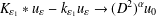Contents
Research Article
AN INFINITE FAMILY OF NINTH DEGREE DIHEDRAL POLYNOMIALS
- Part of:
-
- Published online by Cambridge University Press:
- 14 August 2017, pp. 47-53
-
- Article
-
- You have access
- Export citation
A GENERALISATION OF FINITE PT-GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 07 March 2018, pp. 396-405
-
- Article
-
- You have access
- Export citation
ON A THEOREM OF KANG AND LIU ON FACTORISED GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 08 November 2017, pp. 54-56
-
- Article
-
- You have access
- Export citation
GROUPS OF FINITE NORMAL LENGTH
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2018, pp. 229-239
-
- Article
-
- You have access
- Export citation
CLASSIFICATION OF REFLECTION SUBGROUPS MINIMALLY CONTAINING
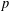 $p$ -SYLOW SUBGROUPS
$p$ -SYLOW SUBGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 04 October 2017, pp. 57-68
-
- Article
-
- You have access
- Export citation
ON
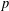 $p$ -PARTS OF CONJUGACY CLASS SIZES OF FINITE GROUPS
$p$ -PARTS OF CONJUGACY CLASS SIZES OF FINITE GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2018, pp. 406-411
-
- Article
-
- You have access
- Export citation
REALISABLE SETS OF CATENARY DEGREES OF NUMERICAL MONOIDS
- Part of:
-
- Published online by Cambridge University Press:
- 04 December 2017, pp. 240-245
-
- Article
-
- You have access
- Export citation
COUNTING CONJUGACY CLASSES IN
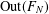 $\text{Out}(F_{N})$
$\text{Out}(F_{N})$
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2018, pp. 412-421
-
- Article
-
- You have access
- Export citation
ON FUNCTIONS ATTRACTING POSITIVE ENTROPY
- Part of:
-
- Published online by Cambridge University Press:
- 04 October 2017, pp. 69-79
-
- Article
-
- You have access
- Export citation
DENSITY, SMITAL PROPERTY AND QUASICONTINUITY
- Part of:
-
- Published online by Cambridge University Press:
- 04 December 2017, pp. 246-252
-
- Article
-
- You have access
- Export citation
TOEPLITZ DETERMINANTS WHOSE ELEMENTS ARE THE COEFFICIENTS OF ANALYTIC AND UNIVALENT FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2018, pp. 253-264
-
- Article
-
- You have access
- Export citation
LEE MONOIDS ARE NONFINITELY BASED WHILE THE SETS OF THEIR ISOTERMS ARE FINITELY BASED
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2018, pp. 422-434
-
- Article
-
- You have access
- Export citation
LANDAU’S THEOREM FOR SOLUTIONS OF THE
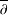 $\overline{\unicode[STIX]{x2202}}$ -EQUATION IN DIRICHLET-TYPE SPACES
$\overline{\unicode[STIX]{x2202}}$ -EQUATION IN DIRICHLET-TYPE SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 28 September 2017, pp. 80-87
-
- Article
-
- You have access
- Export citation
THE SHARP BOUND FOR THE HANKEL DETERMINANT OF THE THIRD KIND FOR CONVEX FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 04 April 2018, pp. 435-445
-
- Article
-
- You have access
- Export citation
INTEGRAL MEANS OF HOLOMORPHIC FUNCTIONS AS GENERIC LOG-CONVEX WEIGHTS
- Part of:
-
- Published online by Cambridge University Press:
- 07 August 2017, pp. 88-93
-
- Article
-
- You have access
- Export citation
AN ENTIRE FUNCTION SHARING TWO VALUES WITH ITS LINEAR DIFFERENTIAL POLYNOMIAL
- Part of:
-
- Published online by Cambridge University Press:
- 04 October 2017, pp. 265-273
-
- Article
-
- You have access
- Export citation
APPLICATIONS OF AN INTERSECTION FORMULA TO DUAL CONES
- Part of:
-
- Published online by Cambridge University Press:
- 17 October 2017, pp. 94-101
-
- Article
-
- You have access
- Export citation
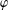 $\unicode[STIX]{x1D711}$ -CONTRACTIBILITY AND
$\unicode[STIX]{x1D711}$ -CONTRACTIBILITY AND 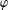 $\unicode[STIX]{x1D711}$ -CONNES AMENABILITY COINCIDE WITH SOME OLDER NOTIONS
$\unicode[STIX]{x1D711}$ -CONNES AMENABILITY COINCIDE WITH SOME OLDER NOTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 30 January 2018, pp. 274-278
-
- Article
-
- You have access
- Export citation
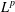 $L^{p}$ -APPROXIMATION OF HOLOMORPHIC FUNCTIONS ON A CLASS OF CONVEX DOMAINS
$L^{p}$ -APPROXIMATION OF HOLOMORPHIC FUNCTIONS ON A CLASS OF CONVEX DOMAINS
- Part of:
-
- Published online by Cambridge University Press:
- 23 April 2018, pp. 446-452
-
- Article
-
- You have access
- Export citation
EXISTENCE OF TRAVELLING WAVES IN THE FRACTIONAL BURGERS EQUATION
- Part of:
-
- Published online by Cambridge University Press:
- 20 December 2017, pp. 102-109
-
- Article
-
- You have access
- Export citation