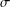 $\unicode[STIX]{x1D70E}$-QUADRATIC FUNCTIONAL EQUATION ON SEMIGROUPS
$\unicode[STIX]{x1D70E}$-QUADRATIC FUNCTIONAL EQUATION ON SEMIGROUPSPublished online by Cambridge University Press: 07 March 2018
Motivated by the notion of Ulam stability, we investigate some inequalities connected with the functional equation 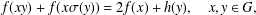 $$\begin{eqnarray}f(xy)+f(x\unicode[STIX]{x1D70E}(y))=2f(x)+h(y),\quad x,y\in G,\end{eqnarray}$$
$$\begin{eqnarray}f(xy)+f(x\unicode[STIX]{x1D70E}(y))=2f(x)+h(y),\quad x,y\in G,\end{eqnarray}$$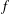 $f$ and
$f$ and 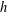 $h$ mapping a semigroup
$h$ mapping a semigroup 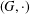 $(G,\cdot )$ into a commutative semigroup
$(G,\cdot )$ into a commutative semigroup 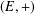 $(E,+)$, where the map
$(E,+)$, where the map 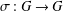 $\unicode[STIX]{x1D70E}:G\rightarrow G$ is an endomorphism of
$\unicode[STIX]{x1D70E}:G\rightarrow G$ is an endomorphism of 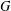 $G$ with
$G$ with 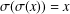 $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D70E}(x))=x$ for all
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D70E}(x))=x$ for all 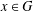 $x\in G$. We derive from these results some characterisations of inner product spaces. We also obtain a description of solutions to the equation and hyperstability results for the
$x\in G$. We derive from these results some characterisations of inner product spaces. We also obtain a description of solutions to the equation and hyperstability results for the 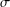 $\unicode[STIX]{x1D70E}$-quadratic and
$\unicode[STIX]{x1D70E}$-quadratic and 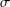 $\unicode[STIX]{x1D70E}$-Drygas equations.
$\unicode[STIX]{x1D70E}$-Drygas equations.