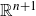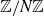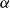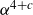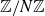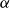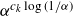Refine search
Actions for selected content:
237327 results in Physics and Astronomy
Foreword
-
- Book:
- Phase Transitions
- Published online:
- 01 May 2025
- Print publication:
- 15 May 2025, pp xi-xii
-
- Chapter
- Export citation
How a self-propelled fin gains hydrodynamic advantages behind a circular cylinder with vortex-induced vibrations
-
- Journal:
- Journal of Fluid Mechanics / Volume 1011 / 25 May 2025
- Published online by Cambridge University Press:
- 15 May 2025, A26
-
- Article
- Export citation
Pressure and vorticity scaling in anguilliform and carangiform swimming
-
- Journal:
- Journal of Fluid Mechanics / Volume 1010 / 10 May 2025
- Published online by Cambridge University Press:
- 15 May 2025, A28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modelling the evolution of Richtmyer–Meshkov mixing width during shock compression phases
-
- Journal:
- Journal of Fluid Mechanics / Volume 1011 / 25 May 2025
- Published online by Cambridge University Press:
- 15 May 2025, A39
-
- Article
- Export citation
Restricted projections to lines in
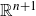 $\mathbb{R}^{n+1}$
$\mathbb{R}^{n+1}$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 15 May 2025, pp. 105-143
- Print publication:
- July 2025
-
- Article
- Export citation
Forced convection in two-phase core-annular flows
-
- Journal:
- Journal of Fluid Mechanics / Volume 1011 / 25 May 2025
- Published online by Cambridge University Press:
- 15 May 2025, A41
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamic plugging of a plane-strain hydraulic fracture driven by slurry flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 1010 / 10 May 2025
- Published online by Cambridge University Press:
- 15 May 2025, A23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Materials Index
-
- Book:
- Phase Transitions
- Published online:
- 01 May 2025
- Print publication:
- 15 May 2025, pp 389-390
-
- Chapter
- Export citation
FUV to FIR SED modelling of NGC 205
-
- Journal:
- Publications of the Astronomical Society of Australia / Volume 42 / 2025
- Published online by Cambridge University Press:
- 15 May 2025, e043
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Appendix - Landau theory and symmetry
-
- Book:
- Phase Transitions
- Published online:
- 01 May 2025
- Print publication:
- 15 May 2025, pp 353-369
-
- Chapter
- Export citation
Frontmatter
-
- Book:
- Phase Transitions
- Published online:
- 01 May 2025
- Print publication:
- 15 May 2025, pp i-iv
-
- Chapter
- Export citation
Contents
-
- Book:
- Phase Transitions
- Published online:
- 01 May 2025
- Print publication:
- 15 May 2025, pp vii-x
-
- Chapter
- Export citation
Part II - Applications
-
- Book:
- Phase Transitions
- Published online:
- 01 May 2025
- Print publication:
- 15 May 2025, pp 101-102
-
- Chapter
- Export citation
4 - Coupling of ferroic degrees of freedom: multiferroics
- from Part II - Applications
-
- Book:
- Phase Transitions
- Published online:
- 01 May 2025
- Print publication:
- 15 May 2025, pp 151-174
-
- Chapter
- Export citation
Uniform sets with few progressions via colourings
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 15 May 2025, pp. 79-103
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
8 - Non-equilibrium phase transitions
- from Part II - Applications
-
- Book:
- Phase Transitions
- Published online:
- 01 May 2025
- Print publication:
- 15 May 2025, pp 272-299
-
- Chapter
- Export citation
General Index
-
- Book:
- Phase Transitions
- Published online:
- 01 May 2025
- Print publication:
- 15 May 2025, pp 391-396
-
- Chapter
- Export citation
Statistical analysis of vertical velocity and buoyancy in convective boundary layers
-
- Journal:
- Journal of Fluid Mechanics / Volume 1011 / 25 May 2025
- Published online by Cambridge University Press:
- 15 May 2025, A40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Self-excited instability and transition to turbulence in laminar separation bubbles induced by surface waviness
-
- Journal:
- Journal of Fluid Mechanics / Volume 1011 / 25 May 2025
- Published online by Cambridge University Press:
- 15 May 2025, A27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
7 - Glassy phenomena in materials with disorder
- from Part II - Applications
-
- Book:
- Phase Transitions
- Published online:
- 01 May 2025
- Print publication:
- 15 May 2025, pp 238-271
-
- Chapter
- Export citation