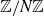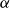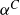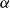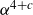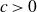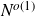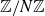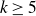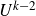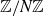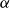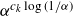1. Introduction
A basic and central fact in additive combinatorics is that the density 3-term arithmetic progressions (3-APs) in a Fourier uniform subset of
$\mathbb{Z}/N\mathbb{Z}$
of density
$\alpha$
is close to
$\alpha^3$
(the random estimate). This fact plays a key role in the proof of Roth’s theorem on the existence of 3-APs in dense subsets of the integers [
Reference Roth8
]. Also important is that Fourier uniformity does not control 4-AP counts—a now-standard construction gives Fourier-uniform sets of density
$\alpha + o(1)$
and 4-AP density much higher than the random estimate of
$\alpha^4$
:
$\{n \in \mathbb{Z}/N\mathbb{Z} : 0 \le n^2 \pmod N \lt \alpha N\}$
. This construction was given by Gowers [
Reference T. Gowers5
] in his groundbreaking work giving a new proof of Szemerédi’s theorem that led to the development of higher order Fourier analysis. On the other hand, is there a Fourier uniform set with very few 4-APs? This is the question that we study in this paper. Interestingly, the above construction does not easily suggest any modifications with too few 4-APs.
1·1. Fourier uniform sets with few 4-APs
We say that
$A \subset \mathbb{Z}/N\mathbb{Z}$
is
$\varepsilon$
-Fourier uniform if
$\lvert\widehat{1_A}(r)\rvert \le \varepsilon$
for all
$r \ne 0$
. Here the Fourier transform is defined as, for
$f \colon \mathbb{Z}/N\mathbb{Z} \to \mathbb{C}$
and
$r \in \mathbb{Z}/N\mathbb{Z}$
,
\[\widehat{f} (r) \;:\!=\; \mathbb{E}_{n \in \mathbb{Z}/N\mathbb{Z}} f(n) e^{-2\pi i rn/N}.\]
In a finite abelian group G (typically
$\mathbb{Z}/N\mathbb{Z}$
for us), for any
$k \ge 3$
and functions
$f_1, \ldots, f_k \colon G \to \mathbb{C}$
, define
\[\Lambda_k(f_1, \ldots, f_k) \;:\!=\; \mathbb{E}_{n, d} f_1(n) f_2(n+d) \cdots f_k(n+(k-1)d).\]
Also
\[\Lambda_k(f) \;:\!=\; \Lambda_k(f, f, \ldots, f) = \mathbb{E}_{n, d} f(n) f(n+d) \cdots f(n+(k-1)d).\]
Given
$A \subset \mathbb{Z}/N\mathbb{Z}$
, we call
$\Lambda_k(1_A)$
the k-AP density of A. It is the number of k-APs in A divided by
$N^2$
, where we count each k-AP twice (forward and backward) and each trivial k-AP (with common difference zero) once.
Gowers initially conjectured that a Fourier uniform subset of
$\mathbb{Z}/N\mathbb{Z}$
of density
$\alpha$
should have 4-AP density at least
$\alpha^4 +o(1)$
.
Conjecture 1·1 (Gowers [
Reference T. Gowers5
, conjecture 4·1]). For every
$\varepsilon \gt 0$
, there exist
$\eta \gt 0$
so that any
$\eta$
-Fourier uniform
$A \subset \mathbb{Z}/N\mathbb{Z}$
with
$\left\lvert A\right\rvert \ge \alpha N$
has
$\Lambda_4(1_A) \ge \alpha^4 - \varepsilon$
.
Gowers subsequently disproved his conjecture by constructing a counterexample with 4-AP density less than
$\alpha^{4+c}$
for some absolute constant
$c \gt 0$
.
Theorem 1·2 (Gowers [
Reference Gowers4
, theorem 6]). There exists some constant
$c \gt 0$
and sets
$A_N \subset \mathbb{Z}/N\mathbb{Z}$
so that
$\left\lvert A_N\right\rvert/N \ge 1/2 + o(1)$
,
$A_N$
is o(1)-Fourier uniform, and
$\Lambda_4(1_{A_N}) \le 2^{-4} - c$
.
It will be convenient to introduce the following definition.
Definition 1·3 (Minimum 4-AP density in a Fourier uniform set). For any
$0 \lt \alpha \lt 1$
, let
$\rho_4(\alpha)$
be the largest real number so that for any
$\varepsilon \gt 0$
there exist
$\eta \gt 0 $
and
$N_0$
so that every
$\eta$
-Fourier uniform
$A \subset \mathbb{Z}/N\mathbb{Z}$
with
$N \ge N_0$
and
$\left\lvert A\right\rvert \ge (\alpha-\varepsilon) N$
has
$\Lambda_4(1_A) \ge \rho_4(\alpha) - \varepsilon$
.
Gowers’ construction [
Reference Gowers4
] shows that
$\rho_4(1/2)\leq 2^{-4}-2^{-30} \lt (1/2)^{4+c}$
for
$c\approx2\times 10^{-8}$
. Via a tensor power trick, this implies
$\rho_4(\alpha) \lt \alpha^{4+c}$
for all sufficiently small
$\alpha$
. Wolf [
Reference Wolf10
] modified this construction to obtain
$\rho_4(1/2)\leq 2^{-4}-({2\times 36})/({9(5\times 18)^22^{12}}) \lt (1/2)^{4+c}$
for
$c\approx5\times 10^{-6}$
. Again this implies that
$\rho_4(\alpha) \lt \alpha^{4+c}$
for all sufficiently small
$\alpha$
. In Corollary 1·9 below of our main results, we improve these bounds to
$\rho_4(\alpha) \lt \alpha^{4.4}$
for all sufficiently small
$\alpha \gt 0$
.
Ruzsa [
Reference Croot and Lev3
, problem 3·2] asked whether
$\rho_4(\alpha)$
goes to zero faster than any polynomial in
$\alpha$
. We believe that the answer should be yes, and we state it as a conjecture. One reason to believe this conjecture is that it would be consistent with the intuition that Fourier uniformity does not control 4-AP counts.
Conjecture 1·4 (Ruzsa’s question). For every
$C \gt 0$
, one has
$\rho_4(\alpha) \lt \alpha^C$
for all sufficiently small
$\alpha$
.
Remark 1.5. Current upper bounds [
Reference Green and Tao6
] on the maximum size of a 4-AP-free subset of [N] (i.e., Szemerédi’s theorem for 4-APs) imply
$\rho_4(\alpha) \ge \exp(-\alpha^{-\Omega(1)})$
, even if we forget the uniformity requirement in the definition of
$\rho_4$
. We do not know any better lower bounds. Conversely, each lower bound on
$\rho_4(\alpha)$
, together with the standard density increment proof strategy of Roth’s theorem, would imply some upper bound on Szemerédi’s theorem for 4-APs.
We pose a conjecture in arithmetic Ramsey theory and show that it would imply Conjecture 1·4. Here a 4-AP
$n, n+d, n+2d, n+3d$
with
$d \ne 0$
is said to be symmetrically coloured if n and
$n+3d$
have the same colour, and
$n+d$
and
$n+2d$
have the same colour.
Conjecture 1·6 (Avoiding symmetrically coloured 4-APs). For all N, there exists an
$N^{o(1)}$
-colouring of [N] without symmetrically coloured 4-APs.
We were unable to resolve Conjecture 1·6 despite some effort. Here is why we think Conjecture 1·6 might be hard. In a colouring of [N] without symmetrically coloured 4-APs, each colour class must be 4-AP-free. Essentially all known constructions of large 4-AP-free sets are related to the famous Behrend construction [ Reference Behrend1 ], coming from high-dimensional convex bodies. However, it seems difficult to avoid symmetrically coloured 4-APs by using Behrend-like sets as colour classes.
We prove the following quantitative version of Theorem 1·7.
Theorem 1·8. Suppose there exists an r-colouring of
$\mathbb{Z}/N\mathbb{Z}$
avoiding symmetrically coloured 4-APs. Then there exists a constant C (depending on r, N), such that for all
$0 \lt \alpha \lt 1/2$
,
\[ {}\rho_4(\alpha) \le C \alpha^{3 + (1/2) \log_r N}.\]
Here is a 3-colouring of
$\mathbb Z/22\mathbb Z$
that avoids symmetrically coloured 4-APs (found by computer search):
\[1333221232131211333233.\]
This implies the following bound, improving earlier bounds by Gowers [ Reference Gowers4 ] and Wolf [ Reference Wolf10 ].
Corollary 1·9.
$\rho_4(\alpha) = O(\alpha^{3+(1/2)\log_3 22}) = O(\alpha^{4.406})$
.
Here is a family of constructions of Fourier uniform sets in
$\mathbb{Z}/N\mathbb{Z}$
. Fix some Jordan measurable
$S \subset [0,1)^2$
(here S being Jordan measurable is the same as saying that the boundary of S has zero measure, i.e.,
$1_S$
is Riemann integrable) such that the intersection of S with every vertical line with x-coordinate in [0,1) has measure
$\alpha$
. Set
$A_N \subset \mathbb{Z}/N\mathbb{Z}$
to be
\[A_N = \{ n \in \mathbb{Z}/N\mathbb{Z} \colon (n/N \bmod 1, n^2/N \bmod 1) \in S\}.\]
As we will see in Section 2,
$A_N$
is o(1)-Fourier uniform. This construction is quite broad and natural from the perspective of quadratic Fourier analysis. For example, Gowers’ construction [
Reference Gowers4
] is a special case. We will show that Conjecture 1·4, when restricted to constructions of subsets of
$\mathbb{Z}/N\mathbb{Z}$
of this form, is actually equivalent to Conjecture 1·6. We will make the statement of this converse precise in Section 2.
1·2.
$U^{k-2}$
-uniform sets with few k-APs
It is now a standard fact that the Gowers uniformity norms [
Reference T. Gowers5
] control longer APs: a
$U^{k-1}$
-uniform set has k-AP density close to random. So a natural extension of Ruzsa’s 4-AP question is whether there are
$U^{k-2}$
-uniform set with few k-APs.
Recall that for a function
$f\colon G\to\mathbb C$
on a finite abelian group G, the kth Gowers uniformity norm is defined by
\[\|f\|_{U^k}^{2^k}=\mathbb E_{n,h_1,\ldots,h_k\in G}\partial_{h_1}\partial_{h_2}\cdots\partial_{h_k}f(n),\]
where
$\partial_hf(n)=f(n)\overline{f(n-h)}$
. We say that a sequence of sets
$A_N \subset \mathbb Z/N\mathbb Z$
is
$U^k$
-uniform if
$\left\lVert1_{A_N} - \left\lvert A_N\right\rvert/N\right\rVert_{U^k} = o(1)$
. It is a standard fact that Fourier uniformity is equivalent to
$U^2$
uniformity.
Gowers made the following generalisation of Conjecture 1·4 to all even APs.
Conjecture 1·10 (Gowers [
Reference T. Gowers5
, conjecture 4·2]). For every even
$k\ge 4$
and
$\varepsilon \gt 0$
, there exist
$\eta \gt 0$
so that if
$A \subset \mathbb{Z}/N\mathbb{Z}$
satisfies
$\left\lVert1_A - \alpha\right\rVert_{U^{k-2}} \le \eta$
where
$\alpha = \left\lvert A\right\rvert/N$
, then
$\Lambda_k(1_A) \ge \alpha^k - \varepsilon$
.
As mentioned above, this conjecture has been disproved for
$k=4$
. In light of this, it is reasonable to believe that it is false for all
$k\ge 4$
. Furthermore, we conjecture (precise statement to follow) that for each
$k \ge 4$
, there exist
$U^{k-2}$
-uniform sets with density
$\alpha$
and k-AP density less than
$\alpha^C$
, for arbitrarily large C. We prove our conjecture for oddFootnote
1
k, and reduce the conjecture for each even
$k \ge 4$
to a conjecture about avoiding symmetrically coloured k-APs.
Definition 1·11 (Minimum k-AP density in a
$U^{k-2}$
-uniform set.) For any integer
$k \ge 4$
and
$0 \lt \alpha \lt 1$
, let
$\rho_k(\alpha)$
be the largest real number so that for any
$\varepsilon \gt 0$
, there exist
$\eta \gt 0$
and
$N_0$
so that if
$N \ge N_0$
and
$A \subset \mathbb{Z}/N\mathbb{Z}$
satisfies
$\left\lVert1_A - \alpha\right\rVert_{U^{k-2}} \le \eta$
, then
$\Lambda_k(1_A) \ge \rho_k(\alpha) - \varepsilon$
.
Conjecture 1·12 (Ruzsa’s question extended to k-APs). Let
$k \ge 4$
. For every
$C \gt 0$
,
$\rho_k(\alpha) \lt \alpha^C$
for all sufficiently small
$\alpha$
.
We prove Conjecture 1·12 for odd k.
Theorem 1·13 (Odd k). For every odd integer
$k \ge 5$
there is some constant
$c_k \gt 0$
such that
$\rho_k(\alpha) \lt \alpha^{c_k \log(1/\alpha)}$
for all
$0 \lt \alpha \lt 1/2$
.
Ruzsa [
Reference Bergelson, Host and Kra2
] constructed Fourier-uniform sets with density
$\alpha$
and 5-AP density
$\alpha^{c\log(1/\alpha)}$
. The above result is stronger, even for
$k=5$
, since the provided sets are
$U^{k-2}$
-uniform.
For even
$k\geq 4$
, a symmetrically coloured k-AP is some
$n, n+d, \cdots, n+(k-1)d$
with
$d \ne 0$
and where
$n + (i-1)d$
and
$n + (k-i)d$
have the same colour for all
$i = 1, \ldots, k/2$
.
Conjecture 1·14 (Avoiding symmetrically coloured k-APs). Let
$k \ge 4$
be even. For all N, there exists an
$N^{o(1)}$
-colouring of [N] avoiding symmetrically coloured k-APs.
Choosing the colouring uniformly at random, an application of the Lovász local lemma implies that there is an
$O(N^{2/k})$
-colouring of [N] avoiding symmetrically coloured k-APs. On the other hand, any such colouring must also avoid monochromatic k-APs and thus must use at least
$\Omega({\exp}(({\log}\log N)^{c_k}))$
colours, by Leng–Sah–Sawhney’s bound on van der Waerden’s theorem [
Reference Leng, Sah and Sawhney7
]. These are the best bounds that we know of for general k.
Also note that the
$k=4$
case (i.e., Conjecture 1·6) implies Conjecture 1·14 for all k, since each symmetrically coloured k-AP contains a symmetrically coloured 4-AP.
1·3. General patterns
Our results also generalise from k-APs to the setting of arbitrary one-dimensional k-point patterns. The proofs are mostly similar to the k-AP case, though there are some additional technical difficulties.
Definition 1·16. Let
$\mathbf{a} = (a_1, \ldots, a_k)$
have increasing integer coordinates
$a_1 \lt a_2 \lt \cdots \lt a_k$
. We define an
$\mathbf{a}$
-AP to be sequence of the form
$n + a_1 d, \ldots, n + a_k d$
for some n, d, and we say that this
$\mathbf{a}$
-AP is non-trivial if
$d \ne 0$
.
In a finite abelian group G, given functions
$f_1, \ldots, f_k \colon G \to \mathbb{C}$
, define
\[\Lambda_{\mathbf{a}}(f_1, \ldots, f_k) \;:\!=\; \mathbb{E}_{n, d} f_1(n+a_1d) f_2(n+a_2d) \cdots f_k(n+a_kd).\]
Then a k-AP is the same as an
$\mathbf{a}$
-AP with
$\mathbf{a} = (0, 1, \ldots, k-1)$
and
$\Lambda_k$
agrees with
$\Lambda_{\mathbf{a}}$
in this case.
Definition 1·17. (Minimum
$\mathbf{a}$
-AP density in a
$U^{k-2}$
-uniform set). Let
$\mathbf{a} = (a_1, \ldots, a_k)$
have increasing integer coordinates. For
$0 \lt \alpha \lt 1$
, let
$\rho_\mathbf{a}(\alpha)$
be the largest real number so that for any
$\varepsilon \gt 0$
there exist
$\eta \gt 0$
and
$N_0$
so that if
$N \ge N_0$
and
$A \subset \mathbb{Z}/N\mathbb{Z}$
satisfies
$\left\lVert1_A - \alpha\right\rVert_{U^{k-2}} \le \eta$
, then
$\Lambda_\mathbf{a}(1_A) \ge \rho_k(\alpha) - \varepsilon$
.
Conjecture 1·18. (Ruzsa’s question extended to
$\mathbf{a}$
-APs). Let
$k \ge 4$
and
$\mathbf{a} = (a_1, \ldots, a_k)$
have increasing integer coordinates. Then for every
$C \gt 0$
, one has
$\rho_\mathbf{a}(\alpha) \lt \alpha^C$
for all sufficiently small
$\alpha \gt 0$
.
Definition 1·19. We say that
$\mathbf{a} = (a_1, \ldots, a_k)$
is symmetric if k is even and
$a_1 + a_k = a_2 + a_{k-1} = a_3 + a_{k-2} = \cdots$
.
When
$k=4$
and
$\mathbf{a}$
is a symmetric, an
$\mathbf{a}$
-AP corresponds to what is sometimes referred to as a “parallelogram pattern.” We prove Conjecture 1·18 in all cases except when k is even and
$\mathbf{a}$
is symmetric. (Although k being even is already part of the definition of
$\mathbf{a}$
being symmetric, we still remind the reader of the parity of k for emphasis.)
Theorem 1·20.
Let
$\mathbf{a} = (a_1, \ldots, a_k)$
have increasing integer coordinates and
$k \ge 4$
. Suppose either k is odd or
$\mathbf{a}$
is not symmetric. Then there exists a constant
$c \gt 0$
(depending on
$\mathbf{a}$
only) such that
$\rho_\mathbf{a}(\alpha) \lt \alpha^{c \log(1/\alpha)}$
for all
$0 \lt \alpha \lt 1/2$
.
When k is even and
$\mathbf{a}$
is symmetric, our results are analogous to those for k-APs with k even, except that instead of finding an
$N^{o(1)}$
-colouring of [N] avoiding symmetrically coloured k-APs, we need an
$N^{o(1)}$
-colouring of [N] avoiding symmetrically coloured
$\mathbf{a}$
-APs. Here a symmetrically coloured
$\mathbf{a}$
-AP is some
$n + a_1 d, \ldots, n + a_k d$
where
$n+a_id$
and
$n+a_{k-i+1}d$
have the same colour for each
$i =1, \ldots, k/2$
.
Conjecture 1·21 (Avoiding symmmetrically coloured
$\mathbf{a}$
-APs). Let
$k \ge 4$
be even. Let
$\mathbf{a} = (a_1, \ldots, a_k)$
be symmetric with increasing integer coordinates. Then there exists an
$N^{o(1)}$
-colouring of [N] without symmetrically coloured
$\mathbf{a}$
-APs.
Note that Conjecture 1·21 for
$k=4$
implies the conjecture for all even
$k \ge 4$
. Here is our most general reduction result.
2. Constructing uniform sets
As is standard in additive combinatorics, there is no often substantive difference between considering subsets
$A\subseteq \mathbb{Z}/N\mathbb{Z}$
versus functions
$f \colon \mathbb Z/N\mathbb Z\to [0,1]$
for large N, as f can be turned into A via sampling, and all relevant quantities concentrate accordingly, such as
$\Lambda_k(1_A) \approx \Lambda_k(f)$
. We will primarily work with functions from now on.
Let
$\mathbb{T} \;:\!=\; \mathbb{R}/\mathbb{Z}$
be the circle. We say that a Riemann integrable function F on
$\mathbb{T}^2$
has constant first marginal
$\alpha$
if
$\int_\mathbb{T} F(x,y)\,\text dy$
is the constant
$\alpha$
for almost every x. Starting with some fixed Riemann integrable
$F \colon \mathbb{T} \to [0,1]$
, consider
$f_N \colon \mathbb{Z}/N\mathbb{Z} \to [0,1]$
defined by
\begin{equation} f_N(n) = F(n/N \bmod 1, n^{k-2}/N \bmod 1).\end{equation}
This can then be turned into a subset
$A_N \subset \mathbb Z/N\mathbb Z$
by sampling if one wishes. We can deduce the following asymptotics using standard Weyl polynomial equidistribution arguments (see Appendix A for proof sketches). They tell us that our sequence is
$U^{k-2}$
-uniform and has k-AP density approaching
$\widetilde \Lambda_k(F)$
defined below. This gives a broad and natural class of constructions for Ruzsa’s question and its extensions.Footnote
2
Proposition 2·1 (4-AP special case). Given a Riemann integrable
$F \colon \mathbb{T}^2 \to [0,1]$
, define
$f_N$
as in (2·1). If F has constant first marginal
$\alpha$
, then, as
$N \to \infty$
,
\[\left\lVert f_N - \alpha\right\rVert_{U^2} \to 0\]
and
\[\Lambda_4(f_N)\to\mathbb{E}_{\substack{x_1, x_2, x_3, x_4, y_1, y_2, y_4, y_4 \in \mathbb{T}: \\ x_2 - x_1 = x_3 - x_2 = x_4 - x_3 \\ \text{ and } y_1 - 3y_2 + 3y_3 - y_4=0}}F(x_1, y_1)F(x_2, y_2)F(x_3, y_3)F(x_4, y_4).\]
Proposition 2·2.
For
$k\geq 4$
, given a Riemann integrable
$F \colon \mathbb{T}^2 \to [0,1]$
, define
$f_N$
as in (2·1). If F has constant first marginal
$\alpha$
, then, as
$N \to \infty$
,
\[\left\lVert f_N - \alpha\right\rVert_{U^{k-2}} \to 0\]
and
\[\Lambda_k(f_N) \to \widetilde\Lambda_k(F),\]
where
\[\widetilde\Lambda_k(F) \;:\!=\; \mathbb{E}_{(x_1, \ldots, x_k, y_1, \ldots, y_k) \in V} F(x_1, y_1) \cdots F(x_k, y_k),\]
where V is the subset of
$\mathbb{T}^{2k}$
defined by all points
$(x_1, \ldots, x_k, y_1, \ldots, y_k)$
satisfying
\[x_2 - x_1 = \cdots = x_k - x_{k-1}\]
and
\[\sum_{i=0}^{k-1} (\!-\!1)^i\binom{k-1}{i} y_i = 0.\]
The following definition captures the minimum possible k-AP density that can be obtained via such constructions.
Definition 2·3. Let
$\widetilde \rho_k(\alpha)$
denote the infimum of
$\widetilde\Lambda_k(F)$
ranging over all Riemann integrable
$F \colon \mathbb{T}^2 \to [0,1]$
with constant first marginal
$\alpha$
.
Proposition 2·4.
$\rho_k(\alpha) \le \widetilde\rho_k(\alpha)$
for all k and
$\alpha$
.
Conjecture 2·5 (Ruzsa’s question restricted to above constructions). Let
$k \ge 4$
. For every
$C \gt 0$
,
$\widetilde\rho_k(\alpha) \lt \alpha^C$
for all sufficiently small
$\alpha$
.
Note that
$\widetilde\rho_k$
is monotonic, since if
$\alpha \lt \alpha'$
and
$F\colon\mathbb{T}^2\to[0,1]$
has constant first marginal
$\alpha'$
, we see that
$({\alpha}/{\alpha'})F$
has constant first marginal
$\alpha$
and satisfies
$\widetilde\Lambda_k(({\alpha}/{\alpha'})F)=({\alpha^k}/{\alpha'^k})\widetilde\Lambda_k(F)\ge \widetilde\Lambda_k(F)$
.
Now we state our main results in terms of
$\widetilde\rho_k$
.
Theorem 2·6 (Odd k). Let
$k \ge 5$
be odd. There is some constant
$c_k \gt 0$
so that for all
$0 \lt \alpha \lt 1/2$
,
\[ {}\widetilde\rho_k(\alpha) \le \alpha^{c_k \log(1/\alpha)}. {}\]
Theorem 2·7 (
$k=4$
). Suppose there exists an r-colouring of
$\mathbb{Z}/N\mathbb{Z}$
avoiding symmetrically coloured 4-APs. There exists a constant C (depending on r, N), such that for all
$0 \lt \alpha \lt 1$
,
\[ {}\widetilde\rho_k(\alpha) \le C \alpha^{3 + (1/2) \log_r N}.\]
Theorem 2·8 (Even k). Let
$k \ge 4$
be even. Suppose there exists an r-colouring of
$\mathbb{Z}/N\mathbb{Z}$
avoiding symmetrically coloured k-APs. For every
$\varepsilon \gt 0$
, there exists a constant C (depending on
$k, r, N,\varepsilon$
), such that for all
$0 \lt \alpha \lt 1$
,
\[ {}\widetilde\rho_k(\alpha) \le C \alpha^{k-1 + (\!\log_r N)/(k-1) - \varepsilon}.\]
For even
$k \ge 6$
, our quantitative bounds are slightly weaker than for
$k=4$
(the main bottleneck is that we do not know a generalisation of Lemma 3·6 to larger k).
Together with Proposition 2·4, Theorems 2·6 to 2·8 imply Theorems 1·8, 1·13 and 1·15. (The deduction of Theorem 1·15 follows from the observation that if there exists an
$N^{\varepsilon}$
-colouring of [N] avoiding symmetrically coloured k-APs, taking k copies of this colouring gives a
$kN^{\varepsilon}$
-colouring of
$\mathbb Z/kN\mathbb Z$
that avoids symmetrically coloured k-APs.) We prove Theorem 2·6 in Section 4 and Theorems 2·7 and 2·8 in Section 5. The constructions in these sections need some building blocks that we collect in Section 3.
We also prove the following converse to Theorem 2·8. We show that given a function
$F\colon\mathbb{T}^2\to[0,1]$
with constant first marginal and
$\widetilde\Lambda_k(F)$
small, one can extract a colouring of
$\mathbb Z/N\mathbb Z$
with few colours that avoids symmetrically coloured k-APs. See Section 6 for proof.
Theorem 2·9 (Even k converse). Let
$k\geq 4$
be even. Suppose there exist
$C, \alpha_0 \gt 0$
such that such that
$\widetilde\rho_k(\alpha)\le \alpha^C$
for all
$0 \lt \alpha \lt \alpha_0$
. Then for every
$\gamma \gt 1/(C/(2k) - 3k/4)$
, for all sufficiently large N, there exists an
$\left\lceil N^\gamma \right\rceil$
-colouring of
$\mathbb Z/N\mathbb Z$
avoiding symmetrically coloured k-APs.
Recall that Conjecture 1·14 says that there exist
$N^{o(1)}$
-colourings of [N] avoiding symmetrically coloured k-APs. Theorems 2·8 and 2·9 together imply the following equivalence of conjectures.
3. Some building blocks
In our constructions we will need colourings that avoid various configurations. We start by recording a fairly standard fact that a colouring based on Behrend sets avoids many small configurations.
Definition 3·1. A k-pattern is a triple
$(n_1,n_2,n_3)$
, not all equal, satisfying
$a n_1 + b n_2 = (a+b) n_3$
for some positive integers a,b and
$a + b \le k-1$
.
Lemma 3·2.
For every k there is some C so that for every N, there is an r-colouring of
$\mathbb Z/N\mathbb Z$
with
$r \le e^{C \sqrt{\log N}}$
and without monochromatic k-patterns.
To see this, note that a standard extension of Behrend’s construction creates a k-pattern-free subset
$S\subset\mathbb Z/N\mathbb Z$
of size at least
$Ne^{-C\sqrt{\log N}}$
(see, e.g., [
Reference Ruzsa9
, theorem 2·3]). Taking
$2\log N e^{C\sqrt{\log N}}\leq e^{C'\sqrt{\log N}}$
random translates of S covers
$\mathbb Z/N\mathbb Z$
with positive probability, producing a colouring where each colour class is k-pattern-free.
To apply Proposition 2·2 we will need to construct a function F where we have control over
$\widetilde\Lambda_k(F)$
. Recall that
$\widetilde\Lambda_k(F)$
is defined to be the expected value of
$F(x_1,y_1)\cdots F(x_k,y_k)$
over k-tuples of points in
$\mathbb{T}$
where the x-coordinates form a k-AP and the y-coordinates satisfy
\[\text{''the}\ k\text{-binomial equation'':} \qquad\sum_{i=1}^k (\!-\!1)^i \binom{k-1}{i-1} y_i = 0.\]
Following Ruzsa [
Reference Ruzsa9
], we say that a solution
$(n_1,\ldots,n_k)$
to the equation
$\sum_{i=1}^ka_in_i=0$
is trivial if
$\sum_{i:n_i=n}a_i=0$
for all n. For example, the trivial solutions to the 4-binomial equation
$n_1-3n_2+3n_3-n_4=0$
are exactly the solutions satisfying
$n_1=n_4$
and
$n_2=n_3$
.
Lemma 3·3 (Ruzsa [
Reference Ruzsa9
, theorem 2·1]). For every sequence
$a_1, \ldots, a_k$
of nonzero integers with
$a_1 + \cdots + a_k = 0$
, there is some constant
$C = C(a_1, \ldots, a_k)$
so that whenever
$N \gt Cr^{k-1}$
, there is an r-element subset of
$\mathbb{Z}/N\mathbb{Z}$
without non-trivial solutions to
$a_1 n_1 + \cdots + a_k n_k = 0$
.
This proof follows by simply constructing the desired set greedily.
Definition 3·4. For each even
$k \ge 4$
, let
$\beta_k$
be the smallest real number such that the following is true: the largest subset of [N] avoiding non-trivial solutions to the k-binomial equation has size at least
$N^{1/\beta_k - o(1)}$
, where
$o(1) \to 0$
as
$N \to \infty$
.
It follows from Lemma 3·3 that
$\beta_k\leq k-1$
. Though we will not use this fact, it follows from a simple double-counting argument that for each even
$k\geq 4$
we have
$\beta_k\geq k/2$
. We conjecture that
$\beta_k = k/2$
for all even
$k\geq 4$
, though we are only able to prove this in the case of
$k=4$
. This is the reason that Theorem 2·7 is quantitatively stronger than Theorem 2·8.
Remark 3·5.
$(n_1,n_2,\ldots,n_{k/2},n_{k/2},\ldots,n_1)$
is a trivial solution to the k-binomial equation for each even k and each choice of
$n_1,\ldots,n_{k/2}$
. However, not all trivial solutions are of this form. For example, for
$k=14$
the equality
$\binom{13}3+\binom{13}7=\binom{13}4+\binom{13}8$
holds, so
$(a,a,a,b,b,a,a,b,b,a,a,a,a,a)$
is also a trivial solution to the 14-binomial equation.
Lemma 3·6.
For every integer r and
$N \gt Cr^2$
, there exists a set
$S\subseteq\mathbb Z/N\mathbb Z$
of size r, such that if
$a, b, c, d\in S$
satisfies
$a-3b+3c-d=0$
, then
$a=d$
and
$b=c$
.
Proof. Let S consist of the first r positive integers whose base-9 expansion uses only 0,1,2. Suppose
$a + 3c = d + 3b$
for some
$a,b,c,d \in S$
. By comparing both sides in base-3, we find that
$a=d$
and
$b=c$
. The largest element of S is at most
$9r^2$
, so viewing S as a subset of
$\mathbb Z/N\mathbb Z$
for any
$N \gt 36r^2$
has the desired property.
4. Constructing a subset of the 2-torus
To prove Theorems 2·6 to 2·8 we will need to construct an appropriate function
$F\colon\mathbb T^2\to[0,1]$
. We start by constructing a colouring of
$\mathbb Z/N\mathbb Z$
that avoids patterns corresponding to non-trivial solutions of the k-binomial equation.
If
$n_1,\ldots, n_k$
is a trivial solution to the k-binomial equation, then one of the following holds:
-
(i) k is even and
$n_i= n_{k+1-i}$
for all
$i = 1, \ldots, k/2$
; or -
(ii) there is some
$I \subset [k]$
with
$\left\lvert I\right\rvert \ge 3$
and
$\sum_{i \in I} (\!-\!1)^i \binom{k-1}{i-1} = 0$
and
$\{n_{j_i}\}_{i \in I}$
are all equal.
(The converse might not hold since (ii) only considers one of the zero-sum subsets of coefficients.) In light of this we make the following definition.
Definition 4·1 (k-binomial pattern). In a colouring
$\phi \colon G \to [r]$
we say that
$n,n+d,\ldots,n+(k-1)d$
with
$d\neq 0$
is a k-binomial pattern if either of the following holds:
-
(a) k is even and
$\phi(n + id) = \phi(n + (k-1-i)d)$
for each
$i = 1, \ldots, k/2$
; or -
(b) there is some
$I \subset [k]$
with
$\left\lvert I\right\rvert \ge 3$
and
$\sum_{i \in I} (\!-\!1)^i \binom{k-1}{i-1} = 0$
such that
$\{n+(i-1)d\}_ {i \in I}$
, are assigned the same colour under
$\phi$
.
Lemma 4·2 (General construction for k-APs). Let
$k \ge 4$
be an integer. For any
$r\geq 1$
and
$\varepsilon \gt 0$
, suppose there exist:
-
(i) a Jordan measurable r-colouring of
$\mathbb{T}$
such that and
\[\Pr_{x,y\in\mathbb{T}}(x,x+y,\ldots,x+(k-1)y\text{ forms a}\ k\text{-binomial pattern})\leq\varepsilon; \]
-
(ii) an r-element subset of
$\mathbb{Z}/m\mathbb{Z}$
avoiding non-trivial solutions to the k-binomial equation.
Then there is some Jordan measurable
$A \subset \mathbb{T}^2$
such that
$1_A$
has constant first marginal
$1/(2^km)$
and
$\widetilde \Lambda_k(1_A) \leq \varepsilon m^{-k+1}$
.
Proof. Let
$\Phi \colon \mathbb{T} \to [r]$
be an r-colouring with low k-binomial pattern density. Let
$S \subset \mathbb{Z}/m\mathbb{Z}$
be an r-element subset avoiding non-trivial solutions to the k-binomial equation and let
$s_1, \ldots, s_{r}$
be the elements of S.
Define
\[J_j = \left[\frac{s_j}{m}, \frac{s_j}{m} + \frac{1}{2^km}\right) \subset \mathbb{T}, \quad \text{for each } j = 1, \ldots, r.\]
Then set
\[A = \{(x,y)\in\mathbb{T}^2: y\in J_{\Phi(x)}\}.\]
Each vertical slice of A is an interval of length
$1/(2^km)$
with vertical shift determined by the colouring
$\Phi$
and the set S. Thus A has constant first marginal
$1/(2^km)$
.
It remains to show that
$\widetilde \Lambda_k(1_A) \leq \varepsilon m^{-k+1}$
. Suppose
$(x_1, y_1), \ldots, (x_k, y_k) \in A$
where
$x_1, \ldots, x_k$
is a k-AP in
$\mathbb{T}$
and
$\sum_{i=1}^k (\!-\!1)^i \binom{k-1}{i-1} y_i = 0$
in
$\mathbb{T}$
. Then
\[\frac{s_{\Phi(x_i)}}{m} \le y_i \lt \frac{s_{\Phi(x_i)}}{m} + \frac{1}{2^km}, \quad \text{ for each } i = 1, \ldots, k.\]
Since
$\sum_{i=1}^k (\!-\!1)^i \binom{k-1}{i-1} y_i = 0$
in
$\mathbb{T}$
, this implies that
\[\sum_{i=1}^k (\!-\!1)^i \binom{k-1}{i-1}\frac{s_{\Phi(x_i)}}{m}\]
lies within less than
$\frac{1}{2^k m} \sum_{i=1}^k \binom{k-1}{i-1} = \tfrac1{2m}$
of an integer. Thus
\begin{equation*}\sum_{i=1}^k (\!-\!1)^i \binom{k-1}{i-1} s_{\Phi(x_i)} \equiv 0 \pmod m.\end{equation*}
Since S has no non-trivial solutions to the k-binomial equation, the above must be a trivial solution. By the definition of a trivial solution, one of the following must be true:
-
(i) k is even and
$\Phi(x_i) = \Phi(x_{k+1-i})$
for all
$i = 1, \ldots, k/2$
; -
(ii) there is some
$I \subset [k]$
with
$\left\lvert I\right\rvert \ge 3$
and
$\sum_{i \in I} (\!-\!1)^i \binom{k-1}{i-1} = 0$
and
$\{x_i\}_{i \in I}$
, are assigned the same colour under
$\Phi$
.
In other words
$x_1,\ldots,x_k$
must form a k-binomial pattern in
$\Phi$
. By hypothesis, this occurs with probability at most
$\varepsilon$
. Once the
$x_i$
’s are chosen, each
$y_i$
lies in an interval of length
$1/(2^km)$
, subject to a single linear equation
$\sum_{i=1}^k (\!-\!1)^i \binom{k-1}{i-1} y_i=0$
. It follows that
$\widetilde \Lambda_k(1_A) \leq \varepsilon (2^km)^{-k+1}$
, as desired.
To apply Lemma 4·2, it will be convenient to have the following result that turns an r-colouring of [N] without k-binomial patterns into a
$k^2r$
-colouring of
$\mathbb{T}$
with few k-binomial patterns.
Lemma 4·3.
For
$k\geq 4$
, let
$\phi$
be an r-colouring of [N] that avoids monochromatic k-patterns and if k is even also avoids nontrivial symmetrically coloured k-APs. Then there exists a Jordan measurable
$k^2r$
-colouring
$\Phi\colon \mathbb{T}\to[k^2r]$
such that
\[\Pr_{x,y\in\mathbb{T}}(x,x+y,\ldots,x+(k-1)y\text{ forms a}\ k\text{-binomial pattern in }\Phi)\lesssim_k \frac1N.\]
Furthermore, if
$k=4$
, the hypothesis that
$\phi$
avoids monochromatic k-patterns can be dropped.
Proof. We cut
$\mathbb{T}$
into k intervals and colour each with k interlaced copies of
$\phi$
; each of the
$k^2$
copies of
$\phi$
uses a disjoint set of colours. More precisely, partition
$\mathbb{T}$
into
$k^2N$
equal-length intervals
$\{I_{a,b,c}\}_{a,c\in[k];b\in[N]}$
where
\[I_{a,b,c} = \left[ \frac{(a-1)kN+(b-1)k+c-1}{k^2N}, \frac{(a-1)kN+(b-1)k+c}{k^2N} \right) \subset \mathbb{T}.\]
Then define
$\Phi\colon\mathbb{T}\to[k^2r]$
by
$\Phi(x)=((a-1)k+c-1)r+\phi(b)$
for a,b,c such that
$x\in I_{a,b,c}$
. Suppose that
$x_1,\ldots,x_k$
forms a k-binomial pattern in
$\Phi$
. Say
$x_i\in I_{a_i,b_i,c_i}$
. By definition, one of the following holds:
-
(i) k is even and
$\Phi(x_i) = \Phi(x_{k+1-i})$
for all
$i = 1, \ldots, k/2$
; -
(ii) there is some
$I \subset [k]$
with
$\left\lvert I\right\rvert \ge 3$
and
$\sum_{i \in I} (\!-\!1)^i \binom{k-1}{i-1} = 0$
and
$\{x_i\}_{i \in I}$
, are assigned the same colour under
$\Phi$
.
Let us analyse the two cases separately. In both cases, we want to deduce that
$(a_1,b_1,c_1)$
,
$\ldots$
,
$(a_k,b_k,c_k)$
cannot all be distinct.
Suppose (i) holds. Since
$\Phi(x_{i}) = \Phi(x_{k+1-i})$
, we see that
$a_i=a_{k+1-i}$
and
$c_i=c_{k+1-i}$
. Recall that
\[x_i \in I_{a_i,b_i,c_i} = \frac{(a_i-1)N+(b_i-1)}{kN} +\left[\frac{c_i-1}{k^2N},\frac{c_i}{k^2N}\right).\]
For
$i=k/2$
, this implies that the common difference
$x_{k/2+1}-x_{k/2}=d/kN+\delta$
for some
$d\in\{-(N-1),\ldots,N-1\}$
and
$\delta\in(-1/k^2N,1/k^2N)$
. Without loss of generality, suppose that
$\delta\in[0,1/k^2N)$
.
This implies that the smallest
$i \gt k/2+1$
with
$c_i\neq c_{k/2}$
(if it exists) satisfies
$c_i\equiv c_{k/2}+1 \pmod k$
. Similarly, the largest
$i \lt k/2$
with
$c_i \neq c_{k/2}$
satisfies
$c_i \equiv c_{k/2} - 1 \pmod k$
. However, since we assumed that
$c_i= c_{k+1-i}$
for all i, this implies that actually
$c_1=c_2=\cdots=c_k$
.
Since
$|x_{k/2+1}-x_{k/2}| \lt 1/k$
, the same argument shows that
$a_1=a_2=\cdots=a_k$
. Therefore
$b_1,\ldots, b_k$
form a symmetrically coloured k-AP in
$\phi$
. Using the fact that
$\phi$
has no nontrivial symmetrically coloured k-APs, we find that
$b_1 = \cdots = b_k$
.
Now suppose (ii) holds. Since
$\Phi(x_i)$
are equal for all
$i\in I$
, we must have some
$a,c\in[k]$
such that
$a_i=a$
and
$c_i=c$
for all
$i\in I$
. Now we wish to show that three of
$b_1,\ldots,b_k$
form a monochromatic k-pattern in
$\phi$
.
Take
$i_1{ \lt }i_2{ \lt }i_3\in I$
. Since
$x_1,\ldots,x_k$
form a k-AP in
$\mathbb{T}$
we know that
\[(i_3-i_2)(x_{i_2}-x_{i_1})\equiv (i_2-{i_1})(x_{i_3}-x_{i_2})\pmod 1.\]
Using the fact that
\[x_i\in I_{a,b_i,c}=\frac{(a-1)kN+c}{k^2N}+\left[\frac{(b_i-1)k-1}{k^2N},\frac{(b_i-1)k}{k^2N}\right)\]
for all
$i\in I$
, we conclude that
\[\left[(i_3-i_2)\frac{b_{i_2}-b_{i_1}}{kN}+\left(\frac{i_2-i_3}{k^2N},\frac{i_3-i_2}{k^2N}\right)\right]\cap \left[(i_2-i_1)\frac{b_{i_3}-b_{i_2}}{kN}+\left(\frac{i_1-i_2}{k^2N},\frac{i_2-i_1}{k^2N}\right)\right]\neq\emptyset.\]
Since
$i_3-i_1 \lt k$
, this further implies that
\[(i_3-i_2)(b_{i_2}-b_{i_1})\equiv(i_2-i_1)(b_{i_3}-b_{i_2})\pmod{kN}.\]
Finally, since
$|b_{i_2}-b_{i_1}|,|b_{i_3}-b_{i_2}| \lt N$
and
$|i_3-i_2|+|i_2-i_1| \lt k$
, this gives
\[(i_3-i_2)(b_{i_2}-b_{i_1})=(i_2-i_1)(b_{i_3}-b_{i_2}).\]
This implies that either
$b_{i_1},b_{i_2},b_{i_3}$
are a monochromatic k-pattern in
$\phi$
or are all equal. Since the former cannot occur, we conclude that
$b_{i_1}=b_{i_2}=b_{i_3}$
.
In either case we have shown that if
$x_1,\ldots,x_k$
forms a k-binomial pattern in
$\Phi$
then there exist at least two distinct indices
$i\neq i'\in [k]$
such that
$(a_i,b_i,c_i)=(a_{i'},b_{i'},c_{i'})$
, i.e., such that
$x_i,x_{i'}$
lie in the same interval of length
$1/k^2N$
. There are at most
$k^2$
choices for i,i’, and then
$x_{i'}$
lies in the same interval as
$x_i$
with probability
$1/k^2N$
. Finally, once
$x_i,x_{i'}$
are fixed, there are at most k choices for the whole sequence
$x_1,\ldots, x_k$
. Therefore we see that the k-binomial pattern density in
$\Phi$
is at most
$k/N$
, as desired.
Finally if
$k=4$
, note that if (ii) holds, then
$I=\{1,2,3,4\}$
since it corresponds to a subset of
$\{-1,3,-3,1\}$
which sums to 0. Thus case (ii) when
$k=4$
corresponds to a monochromatic 4-AP in
$\Phi$
which was already ruled out by case (i). This completes the proof.
Theorem 2·6 for odd length APs then follows.
Proof of Theorem 2·6. We will apply Lemma 4·2 to prove the claim.
By Lemma 3·2 there is a colouring
$\phi\colon [N] \to [r]$
that avoids monochromatic k-patterns where
$N=r^{\Theta_k(\!\log r)}$
. Since k is odd,
$\phi$
satisfies the hypothesis of Lemma 4·3 and thus there is a
$k^2r$
-colouring
$\Phi\colon\mathbb{T}\to[k^2r]$
with k-binomial pattern density
$\lesssim_k 1/N$
.
Next, by Lemma 3·3, there exists a
$k^2r$
-element subset S of
$\mathbb Z/m\mathbb Z$
avoiding non-trivial solutions to the k-binomial equation, where
$m=\Theta_k(r^{k-1})$
.
Applying Lemma 4·2 to
$\Phi$
and S yields
$1_A\subset \mathbb{T}^2$
with constant first marginal
$1/(2^km)$
and
$\widetilde \Lambda_k(1_A) \lesssim_k m^{-\Theta_k(\!\log m)}$
. By definition
$\widetilde \rho_k(1/(2^km)) \lesssim_k m^{-\Theta_k(\!\log m)}$
. By the monotonicity of
$\widetilde\rho_k$
this implies the desired bound on
$\widetilde\rho_k(\alpha)$
.
5. Even length APs: from colouring to uniform sets
Lemma 5·1 (Tensor power construction). Suppose there exists an r-colouring of
$\mathbb{Z}/N\mathbb{Z}$
avoiding symmetrically coloured k-APs. Then for every positive integer
$\ell$
, there exists an
$r^\ell$
-colouring of
$\mathbb{Z}/N^\ell\mathbb{Z}$
avoiding symmetrically coloured k-APs.
Proof. The idea is to write an element of
$\mathbb{Z}/N^\ell \mathbb{Z}$
in its base N expansion, and then colour each digit separately. More precisely, given
$\phi \colon \mathbb{Z}/N\mathbb{Z} \to [r]$
avoiding symmetrically coloured k-APs, define the colouring
$\psi \colon \mathbb{Z}/N^\ell \mathbb{Z} \to [r]^\ell$
as follows. Every element of
$\mathbb{Z}/N^\ell\mathbb{Z}$
can be written uniquely as
$n = n_0 + n_1 N + \cdots + n_{\ell -1}N^{\ell - 1}$
with
$n_0, \ldots, n_{\ell -1} \in \left\{ 0, 1, \ldots, N-1 \right\}$
. Set
$\psi(x) = (\phi(n_0), \ldots, \phi(n_{\ell -1}))$
. Then
$\psi$
has no symmetrically coloured k-APs. Indeed, suppose
$a_1,\ldots,a_k \in \mathbb{Z}/N^\ell \mathbb{Z}$
is a non-trivial k-AP. Let i to be the index of the least significant base-N digit where
$a_1,\ldots,a_k$
are not all equal. By considering mod
$N^{i+1}$
, the ith digits
$a_{1,i},\ldots,a_{k,i}$
form a non-trivial k-AP in
$\mathbb{Z}/N\mathbb{Z}$
, and thus they are not symmetrically coloured under
$\phi$
. Hence
$a_1,\ldots,a_k$
is not symmetrically coloured under
$\psi$
.
Proof of Theorem 2·7. Suppose there exists an r-colouring of
$\mathbb{Z}/N\mathbb{Z}$
avoiding symmetrically coloured 4-APs. Let
$0 \lt \alpha \lt 1/2$
. By Lemma 5·1, for every positive integer
$\ell$
, there is an
$r^\ell$
-colouring of
$\mathbb{Z}/N^\ell\mathbb{Z}$
that avoids symmetrically coloured 4-APs. By Lemma 4·3, there is a
$16r^\ell$
-colouring of
$\mathbb{T}$
whose density of 4-binomial patterns (i.e., symmetrically coloured 4-APs) is
$\lesssim N^{-\ell}$
. By Lemma 3·6, for some
$m = O(r^{2\ell})$
, there is a
$16r^{\ell}$
-element subset of
$\mathbb Z/m\mathbb Z$
that avoids solutions to the 4-binomial equation. By Lemma 4·2, we obtain
$A \subset \mathbb{T}^2$
with constant first marginal
$1/(16m) \gt rsim r^{-2\ell}$
and
$\widetilde \Lambda_4(1_A) \lesssim N^{-\ell}r^{-6\ell}$
. Thus we can choose
$\ell = (1/2)\log_r(1/\alpha) - O_{r}(1)$
so that the marginals are
$1/(16m) \ge \alpha$
, and we have
\[\widetilde \Lambda_4(1_A) \lesssim N^{-\ell}r^{-6\ell} \lesssim_{N,r} \alpha^{3+(1/2)\log_r N}.\]
This completes the proof by the monotonicity of
$\widetilde\rho_4$
.
Proof of Theorem 2·8. We will apply Lemma 4·2 to prove the claim.
First, we show that there exists a colouring
$\phi\colon [N^\ell] \to [u]$
that avoids monchromatic k-patterns and symmetrically coloured k-APs where
$u=r^\ell e^{O(\sqrt {\ell \log N})}$
. Let
$\psi\colon \mathbb Z/N\mathbb Z \to [r]$
be the r-colouring of
$\mathbb Z/N\mathbb Z$
avoiding symmetrically coloured k-APs. By Lemma 5·1, for any
$\ell \ge 1$
, there exists an
$r^\ell$
-colouring
$\psi_\ell$
of
$\mathbb Z/N^\ell\mathbb Z$
avoiding symmetrically coloured k-APs. We also apply Lemma 3·2 to obtain
$\chi \colon \mathbb Z/N^\ell\mathbb Z\to [e^{O(\sqrt {\ell \log N})}]$
avoiding monochromatic k-patterns. Defining
$\phi$
to be the product colouring of
$\psi_\ell$
and
$\chi$
gives the desired properties.
Then by Lemma 4·3, there is a
$k^2u$
-colouring
$\Phi$
of
$\mathbb{T}$
with k-binomial pattern density
$\lesssim_k N^{-\ell}$
.
Next, by definition of
$\beta_k$
, there exists a
$k^2u$
-element subset S of
$\mathbb Z/m\mathbb Z$
avoiding non-trivial solutions to the k-binomial equation, where
$m=(k^2u)^{1/\beta_k+o_{\ell\to \infty}(1)}$
.
Applying Lemma 4·2 to
$\Phi$
and S yields
$1_A\subset \mathbb{T}^2$
with constant first marginal
\[1/(2^km) \gt rsim_k r^{-\ell/\beta_k+o_{\ell\to\infty}(1)}e^{-O(\sqrt{\ell\log N})}\]
and
\[\widetilde \Lambda_k(1_A) \lesssim_k m^{-k+1}N^{-\ell}\lesssim_k u^{-(k-1)/\beta_k+o_{\ell\to\infty}(1)}N^{-\ell}=r^{-\ell(k-1)/\beta_k+o_{\ell\to\infty}(1)}N^{-(1+o_{\ell\to\infty}(1))\ell}.\]
Taking
$\ell=\beta_k\log_r(1/\alpha)-O_{k,r,N}(1)$
gives
$1/(2^km)\geq\alpha$
for all sufficiently small
$\alpha \gt 0$
and
\[\tilde\Lambda_k(1_A)\lesssim_{N,k,r}\alpha^{(k-1+\log_rN)/\beta_k-o_{\alpha\to0}(1)}.\]
Combining this with the monotonicity of
$\widetilde\rho_k$
and the bound
$\beta_k\leq k-1$
gives the desired result.
6. Extracting a colouring
In this section we prove Theorem 2·9, the converse to our main theorem. We do this via a randomised procedure that extracts a colourings from a function. More precisely, suppose that we are given a function
$F \colon \mathbb{T}^2 \to [0,1]$
with constant first marginal
$\alpha$
and small
$\widetilde \Lambda_k(F)$
. For an appropriate choice of r,N we construct an r-colouring of
$\mathbb Z/N\mathbb Z$
that avoids symmetrically coloured k-APs.
The main idea is as follows. We select
$y_1,y_2,\ldots,y_r\in\mathbb{T}$
at random. We convert F to a partial colouring of
$\mathbb{T}$
by giving x the colour i if i is the smallest integer such that
$F(x,y_i)$
is at least some threshold. We then convert this partial colouring of
$\mathbb{T}$
into a partial colouring of [N] by randomly embedding an N-AP into
$\mathbb{T}$
. We will prove that, assuming r, N are chosen appropriately, with positive probability this partial colouring is actually a full colouring and avoids symmetrically coloured k-APs.
Theorem 2·9 follows immediately from the next lemma.
Lemma 6·1.
For
$k \ge 4$
even there exists
$c_k \gt 0$
such that the following holds. Suppose
$F \colon \mathbb{T}^2 \to [0,1]$
has constant first marginal
$\alpha \in (0,1)$
and
$\widetilde\Lambda_k (F) = \eta$
. Then whenever
\[r \ge (\alpha k)^{-1}\log(1/\eta)\quad\text{and}\quad N \le c_k \eta^{-\frac{1}{2k}} \alpha^{\frac{3k}{4}} (\!\log(1/\eta))^{-\frac{k}{4}},\]
there is an r-colouring of [N] that avoids symmetrically coloured k-APs.
Proof. Pick
$x_0, x_1, y_1, \ldots, y_r \in \mathbb{T}$
independently and uniformly at random. We define
$\phi \colon [N] \to [r]$
by setting
$\phi(i)$
to be the least j such that
$F(x_0 + ix_1, y_j) \ge \alpha/2$
, and leaving
$\phi(i)$
undefined if no such j exists. By Markov’s inequality,
$\mathbb{P}_{x_0,x_1,y_j}(F(x_0+ix_1,y_j) \lt \alpha/2)\leq 1-\alpha/2$
for each choice of i,j. Since the
$y_j$
are independent, by taking a union bound of the choices of i,
\[\mathbb{P}(\phi(i)\ \text{is undefined for some}\ i)\le N \left( 1 - \alpha/2 \right)^r \le N e^{-r \alpha/2} \lt \frac12,\]
provided that
$c_k$
is sufficiently small.
Next, let us upper bound the probability that there exists a symmetrically coloured k-AP. We have
\begin{align*}\eta = \widetilde \Lambda_k(F)&= \mathbb{E}_{\substack{w_0,w_1, z_1, \ldots, z_k: \\ \sum_{i=1}^j(\!-\!1)^i \binom{k-1}{i-1} z_i}= 0} \prod_{i=1}^k F(w_0 + iw_1, z_i)\\&\ge\mathbb{E}_{\substack{w_0,w_1, z_1, \ldots, z_k: \\ \sum_{i=1}^j(\!-\!1)^i \binom{k-1}{i-1} z_i}= 0} \prod_{i=1}^k F(w_0 + iw_1, z_i)F(w_0 + (k+1-i) w_1, z_i)\\&=\mathbb{E}_{w_0, w_1, z} \left( \mathbb{E}_{\substack{z_1, \ldots, z_{k/2}: \\ \sum_{i=1}^{k/2} (\!-\!1)^i \binom{k-1}{i-1} z_i= z}} \prod_{i=1}^{k/2} F(w_0 + iw_1, z_i)F(w_0 + (k+1-i) w_1, z_i) \right)^2\\&\ge\left( \mathbb{E}_{w_0, w_1, z} \mathbb{E}_{\substack{z_1, \ldots, z_{k/2}: \\ \sum_{i=1}^{k/2} (\!-\!1)^i \binom{k-1}{i-1} z_i= z}} \prod_{i=1}^{k/2} F(w_0 + iw_1, z_i)F(w_0 + (k+1-i) w_1, z_i) \right)^2\\&=\left( \mathbb{E}_{w_0, w_1, z_1, \ldots, z_{k/2}} \prod_{i=1}^{k/2} F(w_0 + iw_1, z_i)F(w_0 + (k+1-i) w_1, z_i) \right)^2.\end{align*}
In the second line we used the trivial bound
$F\leq 1$
to insert the
$F(w_0+(k+1-i)w_1,z_i)$
terms.
Given a non-trivial k-AP
$a_1, \ldots, a_k \in [N]$
and a map
$\psi \colon [k] \to [r]$
that is symmetric in the sense of
$\psi(i) = \psi(k+1-i)$
for all
$i \le k/2$
, we have
\begin{align*}&\mathbb{P}_\phi (\phi(a_i) = \psi(i) \text{ for all } i\in[k])\\&\le\mathbb{P}_{x_0, x_1, y_1, \ldots, y_r}\left( F(x_0 + a_i x_1, y_{\psi(i)}) \ge \frac{\alpha}{2}\text{ for all } i\in[k] \right)\\&\le\left( \frac{2}{\alpha} \right)^k \mathbb{E}_{x_0, x_1, y_1, \ldots, y_r} \prod_{i=1}^k F(x_0 + a_i x_1, y_{\psi(i)})\\&\le\left( \frac{2}{\alpha} \right)^k \left( \mathbb{E}_{x_0, x_1} \left( \mathbb{E}_{y_1, \ldots, y_r} \prod_{i=1}^k F(x_0 + a_i x_1, y_{\psi(i)}) \right)^{k/2} \right)^{2/k}\\&=\left( \frac{2}{\alpha} \right)^k \left( \mathbb{E}_{x_0, x_1} \left( \mathbb{E}_{y_1, \ldots, y_r} \prod_{i=1}^{k/2} F(x_0 + a_i x_1, y_{\psi(i)})F(x_0 + a_{k+1-i} x_1, y_{\psi(i)}) \right)^{k/2} \right)^{2/k}\\&\le\left( \frac{2}{\alpha} \right)^k\left( \mathbb{E}_{x_0, x_1, z_1, \ldots, z_{k/2}}\prod_{i=1}^{k/2}F(x_0 + a_i x_1, z_i)F(x_0 + a_{k+1-i} x_1, z_{k+1-i}) \right)^{2/k}\\&\le \left( \frac{2}{\alpha} \right)^k \eta^{1/k}.\end{align*}
Here the third line follows by Markov’s inequality and the fourth by Hölder’s inequality. To see the sixth line we expand the
$(k/2)$
th power and again use the trivial bound of
$F\leq 1$
to drop all but
$k/2$
of the terms in each product. The last line follows from the previous calculation after the change of variables
$w_0=x_0+ax_1$
and
$w_1=dx_1$
where the k-AP
$a_1,\ldots,a_k$
is given by
$a_i=a+id$
.
There are at most
$N^2$
choices for the k-AP
$a_1, \ldots, a_k \in [N]$
and at most
$r^{k/2}$
choices for
$\psi$
, so by a union bound we have
\[\mathbb{P}(\phi \text{ contains a symmetrically coloured}\ \textit{k}\text{-AP})\le N^2 r^{k/2} \left( \frac{2}{\alpha} \right)^k \eta^{1/k} \lt \frac12.\]
The last inequality follows for
$r=\lceil(\alpha k)^{-1}\log(1/\eta)\rceil$
and
$c_k$
sufficiently small. It follows that with positive probability,
$\phi$
is an r-colouring of [N] avoiding symmetrically coloured k-APs.
7. General patterns
In this section, we prove Theorem 1·20 and Theorem 1·22. While the main proof strategy is the same as before, there are some additional technical challenges that we need to address.
Definition 7·1. Let
$\mathbf{a} = (a_1, \ldots, a_k)$
have increasing integer coordinates. The
$\mathbf{a}$
-coefficients
$c(\mathbf{a})=(c_1, \ldots, c_k)$
are defined as
$c_i = \prod_{j\ne i} (a_i - a_j)$
for
$1\le i\le k$
. Define the
$\mathbf{a}$
-binomial equation in variables
$n_1,\ldots,n_k$
to be
\[\sum_{i=1}^kn_i/c_i=0.\]
Note that for
$\mathbf{a}=(0,1,\ldots,k-1)$
we have
$c_i=(\!-\!1)^{k-i}(i-1)!(k-i)!$
so in this case the
$\mathbf{a}$
-binomial equation agrees with the k-binomial equation (up to a constant multiplicative factor of
$(\!-\!1)^k(k-1)!$
). The reason the k-binomial equation appears for k-APs is because the
$(k-2)$
nd power of a k-AP satisfies the k-binomial equation. More precisely we have the equality of polynomials
\begin{equation}\sum_{i=1}^k(\!-\!1)^i\binom{k-1}{i-1} (x+(i-1)y)^{k-2}=0.\end{equation}
We first show that this property extends to the
$\mathbf{a}$
-binomial equation for all
$\mathbf{a}$
.
Lemma 7·2.
Let
$\mathbf{a} = (a_1, \ldots, a_n)$
have increasing integer coordinates. Say
$c(\mathbf{a})=(c_1, \ldots, c_n)$
are the corresponding
$\mathbf{a}$
-coefficients. Then we have the equality of polynomials
$\sum_{i=1}^n (x+a_iy)^{n-2}/c_i=0$
.
Proof. We first show that
$\sum_{i=1}^n a_i^t/c_i=0$
holds for any
$0\le t\le n-2$
. Since the
$a_i$
are distinct, it suffices to show that
$\prod_{1\leq j{ \lt }k\leq n}(a_j-a_k)\sum_{i=1}^n a_i^t/c_i=0$
. Expanding, this reduces to showing that
\begin{equation*}f_t\;:\!=\;\sum_{i=1}^n (\!-\!1)^ia_i^t\prod_{\genfrac{}{}{0pt}{}{1\leq j{ \lt }k\leq n}{j,k\neq i}}(a_j-a_k)=0\qquad\text{for all }0\leq t\leq n-2.\end{equation*}
It is easy to check that
$f_t(a_1,\ldots,a_\ell,a_{\ell+1},\ldots,a_n)=-f_t(a_1,\ldots,a_{\ell+1},a_\ell,\ldots,a_n)$
for all
$\ell$
. This implies that
$f_t$
is an alternating polynomial. Since every alternating polynomial is a multiple of the Vandermonde polynomial
$V(a_1,\ldots,a_n)=\prod_{1\leq i \lt j\leq n}(a_i-a_j)$
and
$\deg f_t=\binom{n-1}2+t \lt \binom n2=\deg V$
, we conclude that
$f_t= 0$
for
$t\leq n-2$
.
Therefore
$\sum_{i=1}^n a_i^t/c_i=0$
holds for each
$0\le t\le n-2$
, so every coefficient of the polynomial
$\sum_{i=1}^n (x+a_iy)^{n-2}/c_i$
is 0, as desired.
We then have the following analogue of Proposition 2·2.
Proposition 7·3.
Given a Riemann integrable
$F \colon \mathbb{T}^2 \to [0,1]$
, define
$f_N \colon \mathbb{Z}/N\mathbb{Z} \to [0,1]$
by
$f_N(n) = F(n/N,n^{k-2}/N)$
. If F has constant first marginal
$\alpha$
, then, as
$N \to \infty$
,
\[\left\lVert f_N - \alpha\right\rVert_{U^{k-2}} \to 0\]
and
\[\Lambda_\mathbf{a}(f_N) \to \widetilde\Lambda_\mathbf{a}(F),\]
where
\[\widetilde\Lambda_\mathbf{a}(F) \;:\!=\; \mathbb{E}_{(x_1, \ldots, x_k, y_1, \ldots, y_k) \in V} F(x_1, y_1) \cdots F(x_k, y_k)\]
where V is the subset of
$\mathbb{T}^{2k}$
defined by all points
$(x_1, \ldots, x_k, y_1, \ldots, y_k)$
where
$x_1,\ldots,x_k$
is an
$\mathbf{a}$
-AP and
$y_1,\ldots,y_k$
satisfies the
$\mathbf{a}$
-binomial equation.
This proof is identical to that of Proposition 2·2 other than an application of Lemma 7·2 instead of (7·1).
We now want to adapt Definition 4·1 and Lemma 4·2 to this setting. To do so we will need to understand trivial solutions to the
$\mathbf{a}$
-binomial equation.
Definition 7·4. Let
$\mathbf{a} = (a_1, \ldots, a_k)$
have increasing integer coordinates and let
$c(\mathbf{a})=(c_1, \ldots, c_k)$
be the corresponding
$\mathbf{a}$
-coefficients. When k is even, a pairing of
$\mathbf{a}$
is a map
$f\colon[k]\to[k]$
which partitions [k] into pairs (i.e.,
$f(f(i))=i$
for all i and
$f(i)\neq i$
) where
$c_i=-c_{f(i)}$
for all
$i\in[k]$
.
Now it follows from the definition that if
$n_1,\ldots,n_k$
is a trivial solution to the
$\mathbf{a}$
-binomial equation, then at least one of the following holds:
-
(i) k is even and there exists a pairing f of
$\mathbf{a}$
such that
$n_i=n_{f(i)}$
for all
$i\in[k]$
; or -
(ii) there is some
$I\subset [k]$
with
$|I|\geq 3$
and
$\sum_{i\in I}c_i^{-1}=0$
and
$\{n_i\}_{i\in I}$
are all equal to each other.
In light of this observation we make the following definition.
Definition 7·5 (
$\mathbf{a}$
-binomial pattern). Let
$\mathbf{a} = (a_1, \ldots, a_k)$
have increasing integer coordinates and let
$c(\mathbf{a})=(c_1, \ldots, c_k)$
be the corresponding
$\mathbf{a}$
-coefficients. For a colouring
$\phi \colon G \to [r]$
, we say
$n+a_1d, n+a_2d, \ldots, n+a_kd$
with
$d\neq 0$
is an
$\mathbf{a}$
-binomial pattern if either of the following holds:
-
(a) k is even and there is some pairing f of
$\mathbf{a}$
such that
$\phi(n + a_id) = \phi(n + a_{f(i)}d)$
for each
$i\in[k]$
; or -
(b) there is some
$I \subset [k]$
with
$\left\lvert I\right\rvert \ge 3$
and
$\sum_{i \in I} c_i^{-1} = 0$
such that
$\{n+a_id\}_{i \in I}$
, are assigned the same colour under
$\phi$
.
Remark 7·6. If
$\mathbf{a}$
is symmetric (recall that this means that k is even and
$a_1+a_k=a_2+a_{k-1}=a_3+a_{k-2}=\cdots$
) then clearly
$f(i)=k-i+1$
is a pairing. (We call this pairing the symmetric pairing.) However this is not the only possibility. For example,
$\mathbf{a}=(1,2,10,16,17,20)$
is not symmetric, but
$c(\mathbf{a})=(-41040, 30240, -30240, 5040, -5040, 41040)$
, so
$\mathbf{a}$
has a pairing. Furthermore, consider the symmetric
$\mathbf{a}=(1,2,3,6,7,8)$
. Here
$c(\mathbf{a})=(-420, 120, -120, 120, -120, 420)$
, showing that symmetric
$\mathbf{a}$
can have pairings other than the symmetric one.
Lemma 7·7 (General construction for
$\mathbf{a}$
-AP). Let
$\mathbf{a} = (a_1, \ldots, a_k)$
have increasing integer coordinates. There is a constant
$C_\mathbf{a}$
depending on
$\mathbf{a}$
such that the following holds. For any
$r\geq 1$
and
$\varepsilon \gt 0$
, suppose there exist:
-
(i) a Jordan measurable r-colouring
$\Phi\colon\mathbb{T}\to[r]$
with and
\[\Pr_{x,y\in\mathbb{T}}(x+a_1y,\ldots,x+a_ky\text{ forms an $\mathbf{a}$-binomial pattern})\leq\varepsilon;\]
-
(ii) an r-element subset of
$\mathbb{Z}/m\mathbb{Z}$
avoiding non-trivial solutions to the
$\mathbf{a}$
-binomial equation.
Then there is some Jordan measurable
$A \subset \mathbb{T}^2$
such that
$1_A$
has constant first marginal
$1/(C_\mathbf{a} m)$
and
$\widetilde \Lambda_{\mathbf{a}}(1_A) \leq\varepsilon m^{-k+1}$
.
This lemma follows from the same proof as Lemma 4·2.
We will use Lemma 7·7 to prove Theorems 1·20 and 1·22. To do this we need a colouring that avoids
$\mathbf{a}$
-binomial patterns and a set that avoids non-trivial solutions to the
$\mathbf{a}$
-binomial equation. The latter is produced by Lemma 3·3. The former is harder to produce for
$\mathbf{a}$
-APs than for k-APs. This is due to the presence of non-symmetric pairings. In the next lemmas we show how to produce efficient colourings that avoid all non-symmetric pairings first in
$\mathbb Z/N\mathbb Z$
and then in
$\mathbb{T}$
.
To provide the colouring, we first define a simple colouring of
$\mathbb Z/m\mathbb Z$
that helps to handle wrap-around issues.
Definition 7·8. For an abelian group G and
$p\in G$
, a k-AP with jumps of size p is a sequence
$n_1, \ldots, n_k\in G$
such that there exists
$d\in G$
(the common difference) such that
$n_{i+1}-n_i \in \{d,d+p\}$
for all
$1\le i{ \lt }k$
.
The following lemma is useful for showing that certain APs with jumps are genuine APs.
Lemma 7·9.
Let a,k,p be positive integers, with
$k\leq a$
and p relatively prime to
$a!$
. Let
$G=\mathbb Z$
or
$G=\mathbb Z/m\mathbb Z$
for some m a multiple of
$a!$
. Suppose that
$n_1, \ldots, n_k\in G$
is a k-AP with jumps of size p. If
$n_1\equiv n_k \pmod{a!}$
, then
$n_1, \ldots, n_k$
is a k-AP. Furthermore if there exists
$1 \lt k' \lt k'' \lt k$
, such that
$n_1\equiv n_{k''} \pmod{a!}$
and
$n_{k'}\equiv n_k\pmod{a!}$
, then
$n_1, \ldots, n_k$
is a k-AP.
Proof. Let
$d\in G$
be the common difference. Let
$0\leq c{ \lt }k$
be the number of
$1\leq i{ \lt }k$
such that
$n_{i+1}-n_i= d+p$
. Then
$n_k-n_1=d(k-1)+cp$
.
For the first statement, we have that
$d(k-1)+cp=n_k-n_1\equiv 0 \pmod{a!}$
. Since
$k-1$
is a divisor of
$a!$
we have
$(k-1)\mid (n_k-n_1)$
implying that
$(k-1)\mid cp$
. As p is relatively prime to
$k-1$
, we conclude that either
$c=k-1$
or
$c=0$
, implying that
$n_1, \ldots, n_k$
is an arithmetic progression with common difference
$d+p$
or d. This proves the first result.
For the second statement, we have by the first statement that
$n_1,\ldots, n_{k''}$
is an AP and
$n_{k'},\ldots, n_k$
is an AP. Since
$k' \lt k''$
, this implies that
$n_1,\ldots, n_k$
is a k-AP, as desired.
We will construct the desired colouring using an intricate Behrend-style colouring that avoids the following types of patterns.
Definition 7·10. Let
$\mathbf{a}=(a_1,a_2,a_3,a_4)$
have increasing integer coordinates. In a colouring
$\phi$
, an
$\mathbf{a}$
-ABAB pattern is an
$\mathbf{a}$
-AP
$(n+a_1d,n+a_2d,n+a_3d,n+a_4d)$
such that
$\phi(n+a_1 d)=\phi(n+a_3 d)$
and
$\phi(n+a_2 d)=\phi(n+a_4d)$
. Similarly, an asymmetric
$\mathbf{a}$
-ABBA pattern is an
$\mathbf{a}$
-AP such that
$\phi(n+a_1 d)=\phi(n+a_4 d)$
and
$\phi(n+a_2 d)=\phi(n+a_3d)$
and such that
$\mathbf{a}$
satisfies
$a_1+a_4\neq a_2+a_3$
.
Lemma 7·11.
For all a, there is a constant C such that the following holds. For every
$r\ge 2$
, there exists some
$N=\Theta(r^{C\log r})$
such that there is an r-colouring of
$\mathbb Z/N\mathbb Z$
that avoids
$\mathbf{a}$
-ABAB patterns and asymmetric
$\mathbf{a}$
-ABBA patterns for every
$\mathbf{a}=(a_1,a_2,a_3,a_4)$
with
$0{ \lt }a_1{ \lt }a_2{ \lt }a_3{ \lt }a_4\leq a$
.
Proof. We will pick some appropriate integers M,m where M is relatively prime to
$a!$
. First consider the colouring
$\Psi\colon\{0,1,\ldots,M-1\}^m\to [mM^2]$
defined by
$\Psi(n_1,\ldots,n_m)=n_1^2+\cdots+n_m^2+1$
. First we claim that
$\Psi$
avoids
$\mathbf{a}$
-ABAB patterns and asymmetric
$\mathbf{a}$
-ABBA patterns, for all
$0{ \lt }a_1{ \lt }a_2{ \lt }a_3{ \lt }a_4\leq a$
. To see this, note that for a given
$n, d\in \mathbb Z^m$
, on the line
$n+id$
, the colouring function
$\Psi(n+id)=f_{n,d}(i)$
is a non-trivial quadratic function of i. If
$(n+a_1d,n+a_2d,n+a_3d,n+a_4d)$
is an
$\mathbf{a}$
-ABAB pattern then
$f_{n,d}(a_1)=f_{n,d}(a_3)$
, so the axis of symmetry of the quadratic
$f_{n,d}$
is at
$(a_1+a_3)/2$
. However, as
$f_{n,d}(a_2)=f_{n,d}(a_4)$
, the axis of symmetric would have to be at
$(a_2+a_4)/2 \gt (a_1+a_3)/2$
, contradiction. Similarly, an asymmetric
$\mathbf{a}$
-ABBA pattern is not possible since the axis of symmetry would have to be at
$(a_1+a_4)/2\neq(a_2+a_3)/2$
.
Write
$N=M^m$
and identify
$\mathbb Z/N\mathbb Z$
with
$\{0,1,\ldots,M-1\}^m$
by considering the base M expansion of an element
$0\leq n{ \lt }N$
. Thus we can view
$\Psi$
as a colouring
$\Psi\colon\mathbb Z/N\mathbb Z\to[mM^2]$
.
We will define another colouring
$\chi \colon \{0,1,\ldots,M-1\}^m\to\{0,1,\ldots,a!-1\}^m$
that reduces the coordinates
$\bmod{\,a!}$
. Namely define
$\chi(n_1,\ldots,n_m)=(n_1\mod {a!},\ldots,n_m\mod {a!})$
. Finally define
$\psi\colon\mathbb Z/N\mathbb Z\to[mM^2]\times\{0,1,\ldots,a!-1\}^m$
to be the product of
$\Psi$
and
$\chi$
. We show that
$\psi$
has the desired properties.
To prove this we claim the following. Let
$(n+a_1d,n+a_2d,n+a_3d,n+a_4d)$
be an
$\mathbf{a}$
-AP in
$\mathbb Z/N\mathbb Z$
. If it is an
$\mathbf{a}$
-ABAB pattern or an
$\mathbf{a}$
-ABBA pattern with respect to
$\chi$
, then it is also an
$\mathbf{a}$
-AP when viewed as a subset of
$\{0,1,\ldots,M-1\}^m$
.
This claim follows by verification digit by digit. Suppose that
$(n+a_1d,n+a_2d,n+a_3d,n+a_4d)$
is an
$\mathbf{a}$
-ABAB pattern or an
$\mathbf{a}$
-ABBA pattern with respect to
$\chi$
. Let
$0\leq m_i{ \lt }M$
be the least significant digit in the base M expansion of
$n+id$
. We see that
$m_{a_1}, m_{a_1+1}, \ldots, m_{a_4}$
is an AP with jumps of size M in
$\mathbb Z$
.
Suppose that
$(n+a_1d,n+a_2d,n+a_3d,n+a_4d)$
is an
$\mathbf{a}$
-ABBA pattern. By the definition of
$\chi$
, we know that
$m_{a_1}\equiv m_{a_4}\pmod{a!}$
. By Lemma 7·9,
$m_{a_1}, m_{a_1+1}, \ldots, m_{a_4}$
is a genuine AP. Hence
$m_{a_1},m_{a_2},m_{a_3},m_{a_4}$
form an
$\mathbf{a}$
-AP viewed as elements of
$\{0,1,\ldots,M-1\}$
. Then we can ignore the last digit and induct, since
$((n+a_id)-m_{a_i})/M$
for
$1\le i\le 4$
is an
$\mathbf{a}$
-ABBA pattern in
$\{0,1,\ldots,N/M-1\}$
with respect to
$\chi$
.
Similarly, suppose
$(n+a_1d,n+a_2d,n+a_3d,n+a_4d)$
is an
$\mathbf{a}$
-ABAB pattern. By definition of
$\chi$
,
$m_{a_1}\equiv m_{a_3}\pmod{a!}$
and
$m_{a_2}\equiv m_{a_4}\pmod{a!}$
so by Lemma 7·9,
$m_{a_1}, m_{a_1+1}, \ldots, m_{a_4}$
is an AP. In conclusion,
$m_{a_1}, m_{a_2},m_{a_3},m_{a_4}$
still form an
$\mathbf{a}$
-AP viewed as elements of
$\{0,1,\ldots,M-1\}$
so we can induct as in the previous case.
This completes the proof of the claim.
Thus we have showed that for any
$\mathbf{a}=(a_1,a_2,a_3,a_4)$
with
$a_1{ \lt }a_2{ \lt }a_3{ \lt }a_4\leq a$
any
$\mathbf{a}$
-ABAB pattern or asymmetric
$\mathbf{a}$
-ABBA pattern in the colouring
$\psi$
of
$\mathbb Z/N\mathbb Z$
is actually such a pattern when viewed as a subset of
$\{0,\ldots,M-1\}^m$
. However we chose
$\Psi$
in a way that no such pattern exists.
Picking
$M=\Theta(r^c)$
relatively prime to
$a!$
and
$m=c'\log r$
for appropriate c,c’ gives an r-colouring of
$\mathbb Z/N\mathbb Z$
with
$N\geq r^{\Omega(\!\log r)}$
, as desired.
The reason we study ABAB patterns and asymmetric ABBA patterns is the following lemma which shows that they are ubiquitous in pairings of longer
$\mathbf{a}$
-APs.
Lemma 7·12.
In any pairing f of
$\mathbf{a}$
one of the following holds:
-
(i) there exists
$1\leq i_1{ \lt }i_2{ \lt }i_3{ \lt }i_4\leq k$
with
$f(i_1)=i_3$
and
$f(i_2)=i_4$
; or
-
(ii) there exists
$1\leq i_1{ \lt }i_2{ \lt }i_3{ \lt }i_4\leq k$
with
$f(i_1)=i_4$
and
$f(i_2)=i_3$
and
$a_{i_1}+a_{i_4}\ne a_{i_2}+a_{i_3}$
; or
-
(iii)
$\mathbf{a}$
is symmetric and f is the symmetric pairing
$f(i)=k+1-i$
.
Proof. If there exists some
$2\le i \lt f(1)$
with
$f(i) \gt f(1)$
, then the tuple (1, i, f(1), f(i)) shows we are in case (1).
Now assume that no such i exists. If for any
$2\le i \lt f(1)$
, we have
$a_i+a_{f(i)}\ne a_1+a_{f(1)}$
, then
$(1, \min(i, f(i)), \max(i, f(i)), f(1))$
shows we are in case (2).
Next assume that for all
$2\le i \lt f(1)$
,
$a_i+a_{f(i)}= a_1+a_{f(1)}$
. From this we see that
$|a_1-a_i| | a_1 - a_{f(i)}| = |a_{f(1)} - a_i| | a_{f(1)} - a_{f(i)}|$
for any
$2\le i \lt f(1)$
. For
$i \gt f(1)$
, we have
$|a_1-a_i| \gt |a_{f(1)} - a_i|$
. Thus
\begin{align*}|c_1|&=\prod_{\{i,f(i)\}:i{ \lt }f(1)}|a_1-a_i||a_1-a_{f(i)}|\prod_{i{ \gt }f(1)}|a_1-a_i|\\&\geq\prod_{\{i,f(i)\}:i{ \lt }f(1)}|a_{f(1)}-a_i||a_{f(1)}-a_{f(i)}|\prod_{i{ \gt }f(1)}|a_{f(1)}-a_i|=|c_{f(1)}|.\end{align*}
Note that the inequality is strict unless the product over
$i \gt f(1)$
is empty. Since we know
$|c_1|=|c_{f(1)}|$
this implies that the product is indeed empty, so
$f(1)=k$
.
Thus if we are not in case (1) or (2), we have
$f(1)=k$
and
$a_1+a_k=a_i+a_{f(i)}$
for all
$i\in[k]$
. Thus
$\mathbf{a}$
is symmetric and we see that
$a_{f(1)} \gt a_{f(2)} \gt a_{f(3)} \gt \cdots$
implying that
$f(i)=k+i-1$
for all i, so we are in case (3).
Lemma 7·13.
Let
$\mathbf{a}=(a_1,\ldots,a_k)$
have increasing integer coordinates. There is a constant
$C_\mathbf{a}$
so that the following holds. If k is odd or k is even and
$\mathbf{a}$
is asymmetric, then for every r sufficiently large there exist
$N=\Theta(r^{C_{\mathbf{a}}\log r})$
and an r-colouring
$\Phi$
of
$\mathbb{T}$
such that
\begin{equation}\Pr_{x,y\in\mathbb{T}}(x+a_1y,\ldots,x+a_ky\text{ forms an $\mathbf{a}$-binomial pattern in }\Phi)\lesssim_{\mathbf{a}}\frac1N.\end{equation}
Furthermore, if k is even and
$\mathbf{a}$
is symmetric, if there exists a t-colouring of
$\mathbb Z/N\mathbb Z$
that avoids symmetrically coloured
$\mathbf{a}$
-APs, then there exists an rt-colouring
$\Phi$
of
$\mathbb{T}$
that also satisfies (7·2).
Proof. Without loss of generality, let us assume that
$a_1 \gt 0$
. (This is allowed since all the definitions are invariant under the translation
$(a_1,\ldots,a_k)\leadsto(1,a_2-a_1+1,\ldots,a_k-a_1+1)$
.) Let
$N=\Theta(r^{C_{\mathbf{a}}\log r})$
be an appropriately chosen parameter. We first construct a colouring
$\phi$
of
$\mathbb Z/N\mathbb Z$
that has a stronger property than avoiding
$\mathbf{a}$
-binomial patterns.
By Lemma 3·2, there exists a colouring
$\psi\colon\mathbb Z/N\mathbb Z\to[\!\left\lfloor r^{1/2} \right\rfloor\!]$
that avoids monochromatic
$a_k$
-patterns. When k is odd, let
$\phi=\psi$
, which already avoids
$\mathbf{a}$
-binomial patterns.
When k is even by Lemma 7·11 there is a colouring
$\chi\colon\mathbb Z/N\mathbb Z\to[\!\left\lfloor r^{1/2} \right\rfloor\!]$
that avoids
$(a_{i_1},a_{i_2},a_{i_3},a_{i_4})$
-ABAB patterns for all
$1\leq i_1{ \lt }i_2{ \lt }i_3{ \lt }i_4\leq k$
and also avoids
$(a_{i_1},a_{i_2},a_{i_3},a_{i_4})$
-ABBA patterns for all
$1\leq i_1{ \lt }i_2{ \lt }i_3{ \lt }i_4\leq k$
with
$a_{i_1}+a_{i_4}\neq a_{i_2}+a_{i_3}$
. When k is even and
$\mathbf{a}$
is asymmetric, let
$\phi$
be the product colouring of
$\psi$
and
$\chi$
.
Finally if k is even and
$\mathbf{a}$
is symmetric, let
$\omega\colon\mathbb Z/N\mathbb Z\to[t]$
be the hypothesised colouring that avoids symmetrically coloured
$\mathbf{a}$
-APs. Then let
$\phi$
be the product colouring of
$\psi$
,
$\chi$
, and
$\omega$
.
In each case we have a u-colouring
$\phi\colon \mathbb Z/N\mathbb Z\to[u]$
. By Lemma 7·12, we see that
$\phi$
avoids
$\mathbf{a}$
-binomial patterns. In particular, if k is even and
$\mathbf{a}$
is asymmetric we cannot be in case (3), so we see that
$\phi$
avoids
$\mathbf{a}$
-binomial patterns. Similarly, if k is even and
$\mathbf{a}$
is symmetric, by definition
$\phi$
avoids symmetrically coloured
$\mathbf{a}$
-APs and thus avoids all
$\mathbf{a}$
-binomial patterns.
Now set
$m=(a_k-a_1+1)!$
and define
$\Phi\colon\mathbb{T}\to[mu]$
by interlacing m copies of
$\phi$
, each using disjoint sets of colours. More precisely,
\[\Phi(x)=\phi(\!\left\lfloor Nx \right\rfloor\!)+u(\!\lfloor mNx\rfloor\pmod m).\]
To analyse
$\Phi$
, suppose that
$x+a_1y,\ldots,x+a_ky\in\mathbb{T}$
is an
$\mathbf{a}$
-binomial pattern in
$\Phi$
. Define
$n_i\in \mathbb Z/mN\mathbb Z$
so that
$n_i\equiv \left\lfloor mN(x+iy) \right\rfloor$
and define
$m_i\in[m]$
by
$m_i\equiv \left\lfloor mN(x+iy) \right\rfloor\pmod m$
. Then by definition we have
$\Phi(x+a_iy)=\Phi(x+a_jy)$
if and only if
$m_i=m_j$
and
$\phi(\!\left\lfloor n_i/m \right\rfloor\!)=\phi(\!\left\lfloor n_j/m \right\rfloor\!)$
. We wish to show that for any such
$\mathbf{a}$
-binomial pattern, there must be two distinct indices
$i\neq i'\in[k]$
such that
$n_i=n_{i'}$
.
We know that
$n_{i+1}-n_i\in\{\left\lfloor mNy \right\rfloor,\left\lceil mNy \right\rceil\}$
for each i, so the
$n_i$
form an AP with jumps of size 1. Suppose we have the second type of
$\mathbf{a}$
-binomial pattern; that is, there is some
$\ell\geq 3$
and
$I=\{i_1{ \lt }i_2{ \lt }\cdots{ \lt }i_\ell\}\subset[k]$
such that
$\{x+a_iy\}_{i\in I}$
are assigned the same colour under
$\Phi$
. This implies that
$m_{a_{i_1}}=m_{a_{i_2}}=\cdots=m_{a_{i_\ell}}$
, in particular, that
$n_{a_{i_1}}\equiv n_{a_{i_\ell}}\pmod m$
. Recalling that we chose
$m=(a_k-a_1+1)!$
, we see that Lemma 7·9 implies that
$n_{a_{i_1}},n_{{a_{i_1}}+1},\ldots, n_{a_{i_\ell}}$
is an AP. Pick
$n,d\in \mathbb Z/mN\mathbb Z$
so that
$n+id\equiv n_i\pmod{mN}$
for all
${a_{i_1}}\leq i\leq {a_{i_\ell}}$
. We see that
$(n+a_1d,\ldots,n+{a_k}d)$
is an
$\mathbf{a}$
-binomial pattern in
$\phi$
since
$n+a_jd=n_{a_j}$
for
$i_1\leq j\leq i_\ell$
. By our construction of
$\phi$
, this can only occur if
$n_{a_{i_1}}=n_{{a_{i_1}}+1}=\cdots=n_{a_{i_\ell}}$
.
Similarly, suppose we have the first type of
$\mathbf{a}$
-binomial pattern; that is, there is a pairing f of
$\mathbf{a}$
such that
$\Phi(x+a_iy)=\Phi(x+a_{f(i)}y)$
for all
$i\in[k]$
. We apply Lemma 7·12 to analyse the structure of f.
In case (1), we have
$1\leq i_1{ \lt }i_2{ \lt }i_3{ \lt }i_4\leq k$
with
$f(i_1)=i_3$
and
$f(i_2)=i_4$
. By an identical application of Lemma 7·9 we find that
$n_{a_{i_1}},n_{a_{i_1}+1},\ldots,n_{a_{i_4}}$
is an AP. Therefore
$n_{a_{i_1}},n_{a_{i_2}},n_{a_{i_3}},n_{a_{i_4}}$
form an
$(a_{i_1},a_{i_2},a_{i_3},a_{i_4})$
-ABAB pattern in
$\phi$
. By our construction of
$\phi$
, this can only occur if
$n_{a_{i_1}}=n_{a_{i_1}+1}=\cdots=n_{a_{i_4}}$
.
In case (2), we similarly find that
$n_{a_{i_1}},n_{a_{i_2}},n_{a_{i_3}},n_{a_{i_4}}$
form an asymmetric
$(a_{i_1},a_{i_2},a_{i_3},a_{i_4})$
-ABBA pattern in
$\phi$
and thus get the same conclusion.
Finally in case (3), by the fact that
$f(1)=k$
, we see by Lemma 7·9, that
$n_{a_1},n_{a_1+1},\ldots,n_{a_k}$
is an AP and thus
$n_{a_1},n_{a_2},\ldots,n_{a_k}$
forms a symmetrically coloured
$\mathbf{a}$
-AP in
$\phi$
, again getting the desired conclusion.
Therefore we have shown that if
$x+a_1y,\ldots,x+a_ky\in\mathbb{T}$
form an
$\mathbf{a}$
-binomial pattern in
$\Phi$
, at least two of the terms say
$x+a_iy,x+a_{i'}y$
must lie in the same interval of length
$1/(mN)$
. The probability of this occurring is
$\lesssim_{\mathbf{a}} 1/N$
since there are
$O_k(1)$
choices for i,i’, a
$1/mN$
probability for
$x+a_{i'}y$
to lie in the same interval as
$x+a_iy$
, and
$O_\mathbf{a}(1)$
choices for x,y once
$x+a_iy, x+a_{i'}y$
are fixed. This proves the desired property of
$\Phi$
.
Now Theorems 1·20 and 1·22 follow from the same proofs as Theorems 1·13 and 1·15, using Lemma 7·7 in the place of Lemma 4·2 and using Lemma 7·13 as the colouring input.
Acknowledgements
We thank Zach Hunter for helpful discussions about Lemma 5·1 and colourings without symmetrically coloured 4-APs. We thank Josef Greilhuber for helpful discussions around the constructions in Remark 7·6.
Appendix A. Equidistribution and convergence
Here we prove Proposition 2·2, showing that the various linear form statistics on
$f_N(n) = F(n/N \bmod 1, n^{k-2}/N \bmod 1)$
converge to the associated linear form statistics on F as
$N \to \infty$
. As this is a standard exercise on Weyl equidistribution, we will be somewhat sketchy here.
By a standard square differencing and degree reduction (analogous to Gauss sums), we have the following result, whose proof we omit. Here we use the standard notation
$e(x) = e^{2\pi i x}$
for
$x \in \mathbb{R}$
.
Lemma A.1 (Complete Weyl sums). Let
$P(x_1, \ldots, x_s)$
be a fixed non-constant polynomial with integer coefficients. Then, as
$N \to \infty$
,
\[\frac{1}{N^s} \sum_{n_1, \ldots, n_s =1}^N e\left( \frac{P(n_1, \ldots, n_s)}{N} \right) \to 0.\]
Let us first illustrate the proof of
$\Lambda_k(f_N) \to \widetilde\Lambda_k(F)$
. We consider a multilinear generalisation. Suppose we have smooth
$F_1, \ldots, F_k \colon \mathbb{T}^2 \to [0,1]$
. For each
$j = 1, \ldots, k$
and N, define
$f_{i,N} \colon \mathbb{Z}/N\mathbb{Z} \to [0,1]$
by
$f_{i, N}(n) \;:\!=\; F_i(n/N, n^{k-2}/N)$
. We will show that
\begin{equation}\Lambda_k(f_{1,N}, \ldots, f_{k, N}) \to \widetilde \Lambda_k(F_1, \ldots, F_k), \quad \text{as } N \to \infty\end{equation}
where
$\widetilde\Lambda_k(F_1,\ldots,F_k)$
is the natural multilinear generalisation of
$\widetilde\Lambda_k$
defined by
\[\widetilde\Lambda_k(F_1,\ldots,F_k) \;:\!=\; \mathbb{E}_{(x_1, \ldots, x_k, y_1, \ldots, y_k) \in V} F_1(x_1, y_1) \cdots F_k(x_k, y_k)\]
where V is the subset of
$\mathbb{T}^{2k}$
defined by all points
$(x_1, \ldots, x_k, y_1, \ldots, y_k)$
satisfying
\[x_2 - x_1 = \cdots = x_k - x_{k-1}\]
and
\[\sum_{i=0}^{k-1} (\!-\!1)^i\binom{k-1}{i} y_i = 0.\]
To prove Proposition 2·2, it suffices to prove it assuming that
$F_j$
is smooth, since we can approximate each
$F_j$
from above and below by smooth [0, 1]-valued functions with arbitrary small
$L^1$
approximation error.
Consider the Fourier series expansion
\[F_j(x,y) = \sum_{r,s \in \mathbb{Z}} \widehat{F_{j}}(r,s) e(rx + sy).\]
Since
$F_j$
is smooth, its Fourier coefficients decay faster than any polynomial, i.e.,
$\lvert\widehat{F_j}(r,s)\rvert \lesssim_A (1 + \left\lvert r\right\rvert + \left\lvert s\right\rvert)^{-A}$
for every
$A \gt 0$
. So, due to absolute convergence, we can check (A·1) term-by-term after expanding using the Fourier series. In other words, it suffices to check (A·1) when each
$F_j$
has the form
$F_j(x,y) = e(r_jx + s_jy)$
for some
$r_j, s_j \in \mathbb{Z}$
. In this case, we have
\begin{align*}\text{LHS of } (\text{A}{\cdot}1)&= \mathbb{E}_{n_0, n_1 \in \mathbb{Z}/N\mathbb{Z}} \prod_{j=1}^k f_{j,N}(n_0 + jn_1)\\&= \mathbb{E}_{n_0, n_1 \in \mathbb{Z}/N\mathbb{Z}} \prod_{j=1}^k F_j\left( \frac{n_0 + jn_1}{N}, \frac{(n_0 + jn_1)^{k-2}}{N} \right)\\&=\mathbb{E}_{n_0, n_1 \in \mathbb{Z}/N\mathbb{Z}}e\left( \frac{P(n_0, n_1)}{N} \right)\end{align*}
where
\[P(n_0, n_1) = \sum_{j=1}^k \left( r_j(n_0 + jn_1) + s_j(n_0 + jn_1)^{k-2} \right).\]
If P is the zero polynomial, then the LHS of (A·1) is one. Otherwise, by Lemma A·1, the LHS of (A·1) converges to zero as
$N \to \infty$
.
Note that P is the zero polynomial if and only if
$\sum_{j=1}^k r_j=\sum_{j=1}^k jr_j=0$
and
\begin{equation}\sum_{j=1}^k s_jj^t=0 \text{ for each }0\leq t\leq k-2.\end{equation}
It is not hard to see that
$s_j = (\!-\!1)^j \binom{k-1}{j-1}\lambda$
satisfies the system (A·2) for each
$\lambda\in\mathbb R$
. (See Lemma 7·2 for the proof of a more general identity.) Furthermore these are the only solutions to (A·2) since the matrix
$(j^t)_{j\in[k], 0\leq t\leq k-2}$
is the Vandermonde matrix which is full rank.
On the other hand,
\begin{align*}\text{RHS of } (\text{A}{\cdot}1)&= \mathbb{E}_{x_0, x_1, y_1, \ldots, y_k \in \mathbb{T} \colon \sum_{j=1}^k (\!-\!1)^j \binom{k-1}{j-1} y_j = 0} \prod_{j=1}^k F(x_0 + jx_1, y_j)\\&= \mathbb{E}_{x_0, x_1, y_1, \ldots, y_k \in \mathbb{T} \colon \sum_{j=1}^k (\!-\!1)^j \binom{k-1}{j-1} y_j = 0}\prod_{j=1}^k e(r_j(x_0 + jx_1) + s_jy_j),\end{align*}
which is equal to one if
\[\sum_{j=1}^k \left( r_j(x_0+jx_1)+s_jy_j \right) = 0 \text{ for all } x_0, x_1, y_1, \ldots, y_k \in \mathbb{T} \text{ such that } \sum_{j=1}^k (\!-\!1)^j \binom{k-1}{j-1} y_j = 0 \]
and is equal to zero otherwise. The above is true if and only if there is some
$\lambda \in \mathbb{R}$
such that
\[\sum_{j=1}^k r_j = 0,\quad\sum_{j=1}^k j r_j = 0,\text{ and }s_j = (\!-\!1)^j \binom{k-1}{j-1}\lambda \text{ for each } 1 \le j \le n.\]
This condition is precisely equivalent to P being the zero polynomial, meaning that (A·1) holds when the
$F_1, \ldots, F_k$
are exponential phases. The general result follows from summing the terms of the Fourier series expansion of each
$F_j$
.
The proof for
$\left\lVert f - \alpha\right\rVert_{U^{k-2}}$
is similar but cumbersome to write out. Let us just illustrate the proof in the representative case of
$k = 4$
. It suffices to prove that, given Riemann integrable functions
$F_{00}, F_{01}, F_{10}, F_{00} \colon \mathbb{T}^2 \to [0,1]$
, defining, for each
$j \in \left\{ 00,01,10,11 \right\}$
,
$f_{j,N} \colon \mathbb{Z}/N\mathbb{Z} \to [0,1]$
by
$f_{j,N}(n) = F_{j}(n/N, n^2/N)$
, and letting
$F_j^1$
be the first marginal of
$F_j$
, defined by
$F_j(x)\;:\!=\;\int_\mathbb{T} F(x,y)\,\text dy$
we have, as
$N \to \infty$
,
\begin{multline} \mathbb{E}_{n_0, n_1, n_2 \in \mathbb{Z}/N\mathbb{Z}} f_{00} (n_0) f_{10}(n_0 + n_1) f_{01}(n_0 + n_2) f_{11}(n_0 + n_1 + n_2)\\\to\mathbb{E}_{x_0,x_1,x_2 \in \mathbb{T}} F_{00}^1(x_0) F_{10}^1(x_0+x_1) F_{01}^1(x_0+x_2) F_{11}^1(x_0+x_1+x_2).\end{multline}
As earlier, by approximating with smooth functions, and then considering Fourier series, it suffices to prove this convergence when each
$F_j$
is an exponential phase
$F_j(x,y) = e(r_jx + s_jy)$
, in which case
\begin{align*}\text{LHS of } (\text{A}{\cdot}3) = \mathbb{E}_{n_0, n_1, n_2} e\left( \frac{P_1(n_0, n_1, n_2) + P_2(n_0, n_1, n_2)}{N} \right),\end{align*}
where
\[P_1(n_0, n_1, n_2) = r_{00} n_0 + r_{10}(n_0 + n_1) + r_{01} (n_0 + n_2) + r_{11} (n_0 + n_1 + n_2)\]
and
\[P_2(n_0, n_1, n_2) = s_{00} n_0^2 + s_{10}(n_0 + n_1)^2 + s_{01} (n_0 + n_2)^2 + s_{11} (n_0 + n_1 + n_2)^2\]
Note that
$P_2$
is identically zero if and only if
$s_{00} = s_{10} = s_{01} = s_{11} = 0$
.
If
$(s_{00}, s_{10}, s_{01}, s_{11}) \ne (0,0,0,0)$
, then by Lemma A·1, the LHS of (A·3) converges to zero, but we also have
$F_j^1$
being the zero function whenever
$s_j \ne 0$
. So (A·3) holds in this case.
On the other hand, if
$(s_{00}, s_{10}, s_{01}, s_{11}) = (0,0,0,0)$
, then only linear exponential phases remain, and it is also straightforward to check that (A·3) holds. Basically, the limit is one if
$P_1$
is identically zero, and zero otherwise.
This completes our sketch of the proof of Proposition 2·2. The remaining details are standard and straightforward.
Open access
