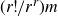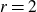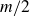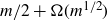Refine search
Actions for selected content:
237328 results in Physics and Astronomy
Rectilinear drift and oscillation of a rotating cylinder placed in flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 1011 / 25 May 2025
- Published online by Cambridge University Press:
- 13 May 2025, A32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Close-contact melting on hydrophobic textured surfaces: confinement and meniscus effects
-
- Journal:
- Journal of Fluid Mechanics / Volume 1010 / 10 May 2025
- Published online by Cambridge University Press:
- 13 May 2025, A46
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pseudo-turbulence induced by settling spheroids in a quiescent fluid
-
- Journal:
- Journal of Fluid Mechanics / Volume 1011 / 25 May 2025
- Published online by Cambridge University Press:
- 13 May 2025, A22
-
- Article
- Export citation
Coupled inflow vapour velocity and surface wettability effect on condensation heat transfer characteristics: a volume-of-fluid method study
-
- Journal:
- Journal of Fluid Mechanics / Volume 1011 / 25 May 2025
- Published online by Cambridge University Press:
- 13 May 2025, A13
-
- Article
- Export citation
The implications of a fluid yield stress
-
- Journal:
- Journal of Fluid Mechanics / Volume 1011 / 25 May 2025
- Published online by Cambridge University Press:
- 13 May 2025, P1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Almost sure upper bound for a model problem for multiplicative chaos in number theory
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 13 May 2025, pp. 29-44
- Print publication:
- July 2025
-
- Article
- Export citation
Spanwise wall forcing can reduce turbulent heat transfer more than drag
-
- Journal:
- Journal of Fluid Mechanics / Volume 1010 / 10 May 2025
- Published online by Cambridge University Press:
- 13 May 2025, A59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamic equilibrium of electrochemical bubbles growing on micro-electrodes
-
- Journal:
- Journal of Fluid Mechanics / Volume 1011 / 25 May 2025
- Published online by Cambridge University Press:
- 13 May 2025, A23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Experimental study of velocity statistics in wall-bounded turbulent emulsions
-
- Journal:
- Journal of Fluid Mechanics / Volume 1011 / 25 May 2025
- Published online by Cambridge University Press:
- 13 May 2025, A14
-
- Article
- Export citation
Resonant standing internal waves in a basin filled with two liquids separated by a pycnocline
-
- Journal:
- Journal of Fluid Mechanics / Volume 1011 / 25 May 2025
- Published online by Cambridge University Press:
- 13 May 2025, A16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Drift of a semi-permeable vesicle through an osmotic gradient: anomalous velocity amplification due to a proximate wall
-
- Journal:
- Journal of Fluid Mechanics / Volume 1011 / 25 May 2025
- Published online by Cambridge University Press:
- 13 May 2025, A18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic coefficients of the attached-eddy model derived from an adiabatic atmosphere
-
- Journal:
- Journal of Fluid Mechanics / Volume 1011 / 25 May 2025
- Published online by Cambridge University Press:
- 13 May 2025, A29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On inhomogeneous Poissonian pair correlations
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 13 May 2025, pp. 17-27
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Orbifold Euler characteristics for compactified universal Jacobians over
 $\overline{\mathcal{M}}_{g,\,n}$
$\overline{\mathcal{M}}_{g,\,n}$
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 13 May 2025, pp. 1-16
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Near-wall effect on vortex dynamics in the flow around a rectangular cylinder
-
- Journal:
- Journal of Fluid Mechanics / Volume 1011 / 25 May 2025
- Published online by Cambridge University Press:
- 13 May 2025, A21
-
- Article
- Export citation
Mathematically established chaos and forecast of statistics with recurrent patterns in Taylor–Couette flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 1011 / 25 May 2025
- Published online by Cambridge University Press:
- 13 May 2025, R2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Transient motion of a swimming sheet in the inertial regime
-
- Journal:
- Journal of Fluid Mechanics / Volume 1011 / 25 May 2025
- Published online by Cambridge University Press:
- 13 May 2025, A2
-
- Article
- Export citation
Large cuts in hypergraphs via energy
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 13 May 2025, pp. 45-61
- Print publication:
- July 2025
-
- Article
- Export citation
Transition between rotation- and buoyancy-dominated regimes in rotating convection: the effect of boundary conditions
-
- Journal:
- Journal of Fluid Mechanics / Volume 1011 / 25 May 2025
- Published online by Cambridge University Press:
- 13 May 2025, A7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Collisions of elliptic vortex rings upon flat walls
-
- Journal:
- Journal of Fluid Mechanics / Volume 1011 / 25 May 2025
- Published online by Cambridge University Press:
- 13 May 2025, A19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation