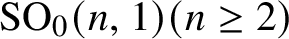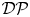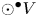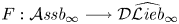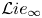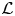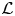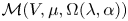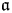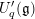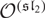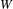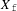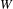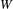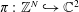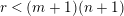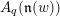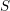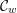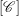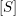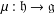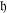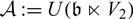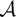Refine listing
Actions for selected content:
264 results in 17Bxx
Vanishing of cohomology and parameter rigidity of actions of solvable Lie groups, II
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 03 November 2020, pp. 3023-3059
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- Export citation
Classification of universal formality maps for quantizations of Lie bialgebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 10 / October 2020
- Published online by Cambridge University Press:
- 27 November 2020, pp. 2111-2148
- Print publication:
- October 2020
-
- Article
- Export citation
A class of simple non-weight modules over the virasoro algebra
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 07 August 2020, pp. 956-970
-
- Article
- Export citation
GENERALISED QUANTUM DETERMINANTAL RINGS ARE MAXIMAL ORDERS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 04 August 2020, pp. 515-525
- Print publication:
- September 2021
-
- Article
- Export citation
Codimension growth for weak polynomial identities, and non-integrality of the PI exponent
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 4 / November 2020
- Published online by Cambridge University Press:
- 20 July 2020, pp. 929-949
-
- Article
- Export citation
SHIFTED COISOTROPIC CORRESPONDENCES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 03 July 2020, pp. 785-849
- Print publication:
- May 2022
-
- Article
- Export citation
CLOSED IDEALS AND LIE IDEALS OF MINIMAL TENSOR PRODUCT OF CERTAIN C*-ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 03 July 2020, pp. 414-425
- Print publication:
- May 2021
-
- Article
- Export citation
Explicit symmetric DGLA models of 3-cells
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 01 July 2020, pp. 368-382
- Print publication:
- June 2021
-
- Article
- Export citation
HIGHER DEFORMATIONS OF LIE ALGEBRA REPRESENTATIONS II
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 244 / December 2021
- Published online by Cambridge University Press:
- 02 June 2020, pp. 232-255
- Print publication:
- December 2021
-
- Article
- Export citation
On the structure of Kac–Moody algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 20 May 2020, pp. 1124-1152
- Print publication:
- August 2021
-
- Article
- Export citation
Monoidal categorification and quantum affine algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 5 / May 2020
- Published online by Cambridge University Press:
- 27 April 2020, pp. 1039-1077
- Print publication:
- May 2020
-
- Article
- Export citation
BGG CATEGORY FOR THE QUANTUM SCHRÖDINGER ALGEBRA
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 20 April 2020, pp. 266-279
- Print publication:
- May 2021
-
- Article
- Export citation
Projective objects and the modified trace in factorisable finite tensor categories
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 26 March 2020, pp. 770-821
- Print publication:
- April 2020
-
- Article
- Export citation
THE
 $q$-SCHUR ALGEBRAS AND
$q$-SCHUR ALGEBRAS AND  $q$-SCHUR DUALITIES OF FINITE TYPE
$q$-SCHUR DUALITIES OF FINITE TYPE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 19 February 2020, pp. 129-160
- Print publication:
- January 2022
-
- Article
- Export citation
Classification of Simple Cuspidal Modules Over a Lattice Lie Algebra of Witt Type
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 13 January 2020, pp. 417-440
- Print publication:
- April 2021
-
- Article
- Export citation
THE SECOND FUNDAMENTAL THEOREM OF INVARIANT THEORY FOR THE ORTHOSYMPLECTIC SUPERGROUP
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 242 / June 2021
- Published online by Cambridge University Press:
- 04 December 2019, pp. 52-76
- Print publication:
- June 2021
-
- Article
- Export citation
Quantum Langlands duality of representations of
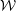 ${\mathcal{W}}$-algebras
${\mathcal{W}}$-algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 12 / December 2019
- Published online by Cambridge University Press:
- 04 October 2019, pp. 2235-2262
- Print publication:
- December 2019
-
- Article
- Export citation
Laurent phenomenon and simple modules of quiver Hecke algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 12 / December 2019
- Published online by Cambridge University Press:
- 04 October 2019, pp. 2263-2295
- Print publication:
- December 2019
-
- Article
- Export citation
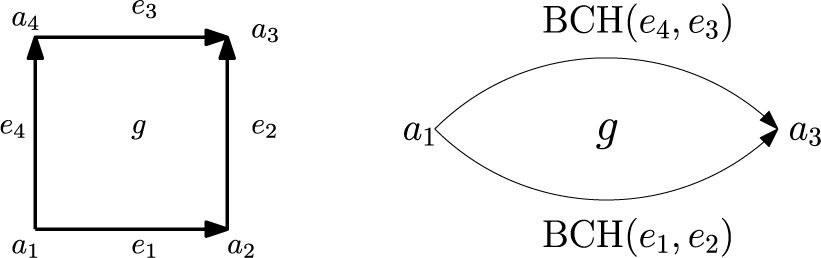
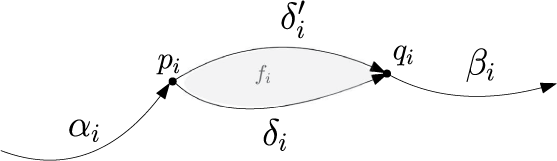
ON 2-HOLONOMY
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 04 September 2019, pp. 145-174
- Print publication:
- April 2021
-
- Article
- Export citation
THE PRIME IDEALS AND SIMPLE MODULES OF THE UNIVERSAL ENVELOPING ALGEBRA U(𝔟⋉V2)
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 62 / Issue S1 / December 2020
- Published online by Cambridge University Press:
- 29 July 2019, pp. S77-S98
- Print publication:
- December 2020
-
- Article
- Export citation