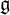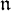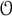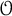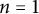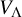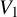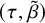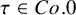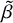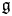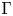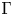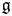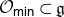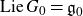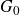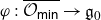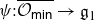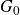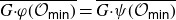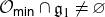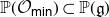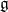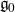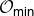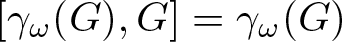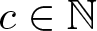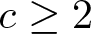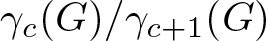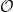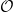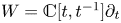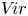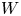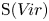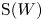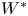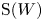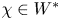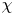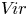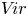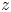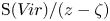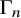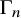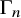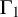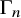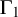Refine listing
Actions for selected content:
264 results in 17Bxx
Classification of simple smooth modules over the Heisenberg–Virasoro algebra
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 17 January 2024, pp. 1321-1365
- Print publication:
- August 2025
-
- Article
- Export citation
Virasoro Constraints for Toric Bundles
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 01 January 2024, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COEFFICIENT QUIVERS,
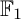 ${\mathbb {F}}_1$-REPRESENTATIONS, AND EULER CHARACTERISTICS OF QUIVER GRASSMANNIANS
${\mathbb {F}}_1$-REPRESENTATIONS, AND EULER CHARACTERISTICS OF QUIVER GRASSMANNIANS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 255 / September 2024
- Published online by Cambridge University Press:
- 13 December 2023, pp. 561-617
- Print publication:
- September 2024
-
- Article
- Export citation
Irreducible modules of modular Lie superalgebras and super version of the first Kac–Weisfeiler conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 554-573
- Print publication:
- September 2024
-
- Article
- Export citation
On the representability of actions of Leibniz algebras and Poisson algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 22 November 2023, pp. 998-1021
-
- Article
- Export citation
Webs of type P
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 27 October 2023, pp. 1917-1966
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Prime representations in the Hernandez–Leclerc category: classical decompositions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 27 October 2023, pp. 1987-2018
- Print publication:
- December 2024
-
- Article
- Export citation
The Frobenius semiradical, generic stabilizers, and Poisson center for nilradicals
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 6 / December 2024
- Published online by Cambridge University Press:
- 27 October 2023, pp. 2019-2048
- Print publication:
- December 2024
-
- Article
- Export citation
Category
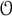 $\mathcal {O}$ for truncated current Lie algebras
$\mathcal {O}$ for truncated current Lie algebras
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 19 October 2023, pp. 1795-1821
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A lattice theoretical interpretation of generalized deep holes of the Leech lattice vertex operator algebra
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 27 September 2023, e86
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Conformal blocks for Galois covers of algebraic curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 29 August 2023, pp. 2191-2259
- Print publication:
- October 2023
-
- Article
- Export citation
Projections of the minimal nilpotent orbit in a simple Lie algebra and secant varieties
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 13 July 2023, pp. 595-624
- Print publication:
- November 2023
-
- Article
- Export citation
Baumslag–Solitar groups and residual nilpotence
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 16 June 2023, pp. 532-547
-
- Article
- Export citation
Cohomology in singular blocks of parabolic category
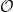 $\mathcal{O}$
$\mathcal{O}$
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 555-568
- Print publication:
- September 2023
-
- Article
- Export citation
Comparison of quantizations of symmetric spaces: cyclotomic Knizhnik–Zamolodchikov equations and Letzter–Kolb coideals
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 02 May 2023, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE QUANTUM ISOMERIC SUPERCATEGORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 25 April 2023, pp. 1077-1124
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Poisson spectrum of the symmetric algebra of the Virasoro algebra
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 5 / May 2023
- Published online by Cambridge University Press:
- 18 April 2023, pp. 933-984
- Print publication:
- May 2023
-
- Article
- Export citation
On the primality of totally ordered q-factorization graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 20 March 2023, pp. 594-637
- Print publication:
- April 2024
-
- Article
- Export citation
Classification of simple Harish–Chandra modules over the Ovsienko–Roger superalgebra
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 14 March 2023, pp. 483-493
- Print publication:
- April 2024
-
- Article
- Export citation
Euler continuants in noncommutative quasi-Poisson geometry
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 October 2022, e88
-
- Article
-
- You have access
- Open access
- HTML
- Export citation







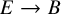
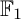
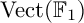
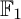
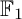
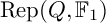
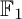
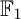
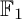
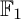
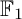
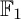
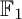
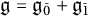
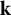
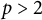
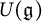
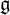
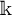
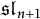
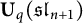
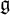
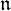
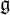
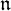
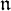
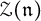 of the symmetric algebra
of the symmetric algebra 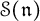 ,
, 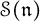 as
as 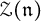 -module, and
-module, and