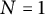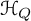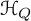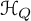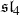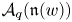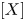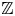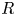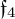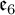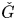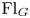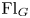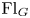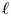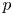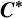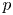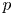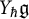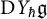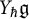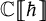Refine listing
Actions for selected content:
264 results in 17Bxx
PRESENTING INFINITESIMAL q-SCHUR ALGEBRAS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 257 / March 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 134-155
- Print publication:
- March 2025
-
- Article
- Export citation
Biderivations of Lie algebras
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 440-450
- Print publication:
- June 2025
-
- Article
- Export citation
Simple weight modules over the
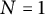 $N=1$ Heisenberg–Virasoro superalgebra
$N=1$ Heisenberg–Virasoro superalgebra
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 16 December 2024, pp. 198-212
- Print publication:
- March 2025
-
- Article
- Export citation
On split quasi-hereditary covers and Ringel duality
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 December 2024, e105
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The spin Brauer category
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 14 November 2024, e98
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN EXAMPLE OF THE JANTZEN FILTRATION OF A D-MODULE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 11 November 2024, pp. 265-296
- Print publication:
- June 2025
-
- Article
- Export citation
Singularities of nilpotent Slodowy slices and collapsing levels of W-algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 November 2024, e95
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
REDUCED QUIVER QUANTUM TOROIDAL ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 07 November 2024, pp. 341-369
- Print publication:
- March 2025
-
- Article
- Export citation
DT INVARIANTS FROM VERTEX ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 20 September 2024, pp. 291-339
- Print publication:
- January 2025
-
- Article
- Export citation
Graded extensions of Verma modules
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 2 / September 2024
- Published online by Cambridge University Press:
- 08 November 2024, pp. 285-311
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Laurent family of simple modules over quiver Hecke algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 September 2024, pp. 1916-1940
- Print publication:
- August 2024
-
- Article
- Export citation
EXCEPTIONAL SIMPLE REAL LIE ALGEBRAS
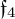 $\mathfrak {f}_4$ AND
$\mathfrak {f}_4$ AND 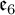 $\mathfrak {e}_6$ VIA CONTACTIFICATIONS
$\mathfrak {e}_6$ VIA CONTACTIFICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 03 July 2024, pp. 157-201
- Print publication:
- January 2025
-
- Article
- Export citation
A classification of automorphic Lie algebras on complex tori
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 28 May 2024, pp. 947-989
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Twisted Whittaker category on affine flags and the category of representations of the mixed quantum group
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 13 May 2024, pp. 1349-1417
- Print publication:
- June 2024
-
- Article
- Export citation
On Donkin's tilting module conjecture II: counterexamples
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 02 May 2024, pp. 1167-1193
- Print publication:
- June 2024
-
- Article
- Export citation
SPHERICAL REPRESENTATIONS FOR
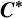 $\boldsymbol C^{\boldsymbol {*}}$-FLOWS III: WEIGHT-EXTENDED BRANCHING GRAPHS
$\boldsymbol C^{\boldsymbol {*}}$-FLOWS III: WEIGHT-EXTENDED BRANCHING GRAPHS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 15 April 2024, pp. 239-272
- Print publication:
- October 2024
-
- Article
- Export citation
Whittaker categories of quasi-reductive lie superalgebras and quantum symmetric pairs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 02 April 2024, e37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Skew group categories, algebras associated to Cartan matrices and folding of root lattices
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 April 2024, pp. 1-45
-
- Article
- Export citation
The restricted quantum double of the Yangian
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 16 February 2024, pp. 770-841
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shi arrangements and low elements in affine Coxeter groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 12 February 2024, pp. 683-713
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 be a commutative ring containing a primitive
be a commutative ring containing a primitive 


 over
over  form an ascending chain of subalgebras of the
form an ascending chain of subalgebras of the  , which are useful in studying representations of the Frobenius kernel of the associated quantum linear group. Let
, which are useful in studying representations of the Frobenius kernel of the associated quantum linear group. Let  be the quantized enveloping algebra of
be the quantized enveloping algebra of 
 . There is a natural surjective algebra homomorphism
. There is a natural surjective algebra homomorphism 
 to
to  . The map
. The map 

 to
to  , where
, where  is a certain Hopf subalgebra of
is a certain Hopf subalgebra of  , which is closely related to Frobenius–Lusztig kernels of
, which is closely related to Frobenius–Lusztig kernels of  . We give the extra defining relations needed to define the infinitesimal
. We give the extra defining relations needed to define the infinitesimal  as a quotient of
as a quotient of  . The map
. The map 
 , where
, where  is the modified quantum algebra associated with
is the modified quantum algebra associated with  . We also give a generating set for the kernel of
. We also give a generating set for the kernel of 
 -modules over a field of characteristic
-modules over a field of characteristic