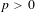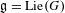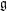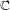Refine listing
Actions for selected content:
264 results in 17Bxx
THE HALL ALGEBRAS OF SURFACES I
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 3 / May 2020
- Published online by Cambridge University Press:
- 22 October 2018, pp. 971-1028
- Print publication:
- May 2020
-
- Article
- Export citation
NILPOTENT SUBSPACES AND NILPOTENT ORBITS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 106 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 30 May 2018, pp. 104-126
- Print publication:
- February 2019
-
- Article
-
- You have access
- Export citation
COHOMOLOGY OF FILIFORM LIE ALGEBRAS OVER FIELDS OF CHARACTERISTIC TWO
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 December 2017, pp. 168-170
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation
ROUQUIER’S CONJECTURE AND DIAGRAMMATIC ALGEBRA
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 16 November 2017, e27
-
- Article
-
- You have access
- Open access
- Export citation
MULTIPLICATIVELY CLOSED MARKOV MODELS MUST FORM LIE ALGEBRAS
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 59 / Issue 2 / October 2017
- Published online by Cambridge University Press:
- 23 October 2017, pp. 240-246
-
- Article
-
- You have access
- Export citation
A NEW FAMILY OF POISSON ALGEBRAS AND THEIR DEFORMATIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 233 / March 2019
- Published online by Cambridge University Press:
- 25 September 2017, pp. 32-86
- Print publication:
- March 2019
-
- Article
-
- You have access
- HTML
- Export citation
Maximal finite abelian subgroups of E 8
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 5 / October 2017
- Published online by Cambridge University Press:
- 29 June 2017, pp. 993-1008
- Print publication:
- October 2017
-
- Article
- Export citation
Higher symmetries of powers of the Laplacian and rings of differential operators
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 08 March 2017, pp. 678-716
- Print publication:
- April 2017
-
- Article
- Export citation
Homomorphisms between standard modules over finite-type KLR algebras
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 3 / March 2017
- Published online by Cambridge University Press:
- 01 March 2017, pp. 621-646
- Print publication:
- March 2017
-
- Article
- Export citation
Generalized and degenerate Whittaker models
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 06 February 2017, pp. 223-256
- Print publication:
- February 2017
-
- Article
- Export citation
SEMISIMPLICITY OF HECKE AND (WALLED) BRAUER ALGEBRAS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 103 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 25 October 2016, pp. 1-44
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
Quivers with loops and generalized crystals
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 10 / October 2016
- Published online by Cambridge University Press:
- 20 July 2016, pp. 1999-2040
- Print publication:
- October 2016
-
- Article
- Export citation
W-ALGEBRAS FROM HEISENBERG CATEGORIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 5 / November 2018
- Published online by Cambridge University Press:
- 13 July 2016, pp. 981-1017
- Print publication:
- November 2018
-
- Article
- Export citation
On the minimal modules for exceptional Lie algebras: Jordan blocks and stabilizers
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 1 / 2016
- Published online by Cambridge University Press:
- 01 July 2016, pp. 235-258
-
- Article
-
- You have access
- Export citation
Finite Groups and Lie Rings with an Automorphism of Order 2n
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 2 / May 2017
- Published online by Cambridge University Press:
- 15 June 2016, pp. 391-412
-
- Article
- Export citation
THE GROUP OF AUTOMORPHISMS OF THE LIE ALGEBRA OF DERIVATIONS OF A FIELD OF RATIONAL FUNCTIONS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 513-524
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
ON THE HOMOGENIZED ENVELOPING ALGEBRA OF THE LIE ALGEBRA Sℓ(2,ℂ) II
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 189-219
- Print publication:
- January 2017
-
- Article
-
- You have access
- Export citation
ABELIAN IDEALS IN A COMPLEX SIMPLE LIE ALGEBRA
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 255-264
- Print publication:
- January 2017
-
- Article
-
- You have access
- Export citation
Application of Lie Algebra in Constructing Volume-Preserving Algorithms for Charged Particles Dynamics
- Part of
-
- Journal:
- Communications in Computational Physics / Volume 19 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 17 May 2016, pp. 1397-1408
- Print publication:
- May 2016
-
- Article
- Export citation
RIGID ORBITS AND SHEETS IN REDUCTIVE LIE ALGEBRAS OVER FIELDS OF PRIME CHARACTERISTIC
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 04 April 2016, pp. 583-613
- Print publication:
- June 2018
-
- Article
- Export citation

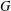
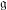
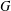
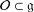
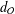
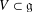
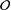
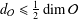
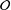
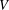
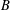
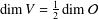
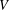
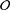
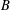
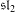
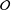
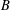

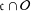

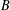

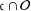

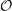
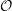
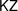
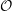
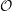
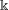

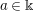
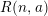
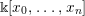
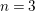

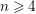
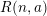
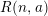
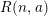
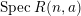
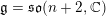
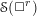

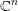
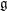
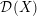
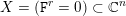

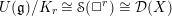
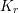

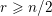
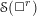
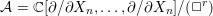
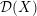
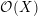
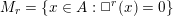
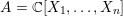
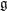
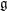
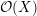
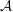
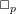
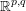
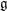
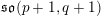
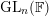

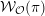
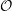
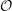
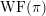
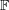
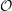
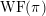
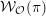
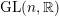
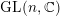

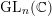
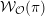
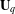
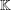
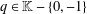
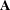
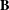
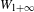
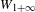
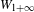
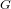
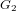
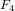
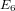
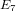

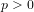

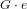
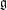

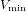
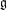
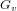
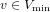
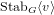
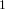
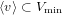
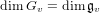
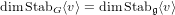
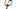 of order 2
of order 2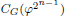 of the involution
of the involution 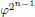 is nilpotent of class
is nilpotent of class 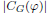 ) be the number of fixed points of
) be the number of fixed points of