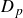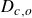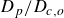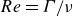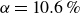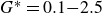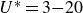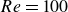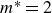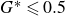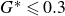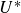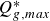Refine search
Actions for selected content:
212053 results in Engineering
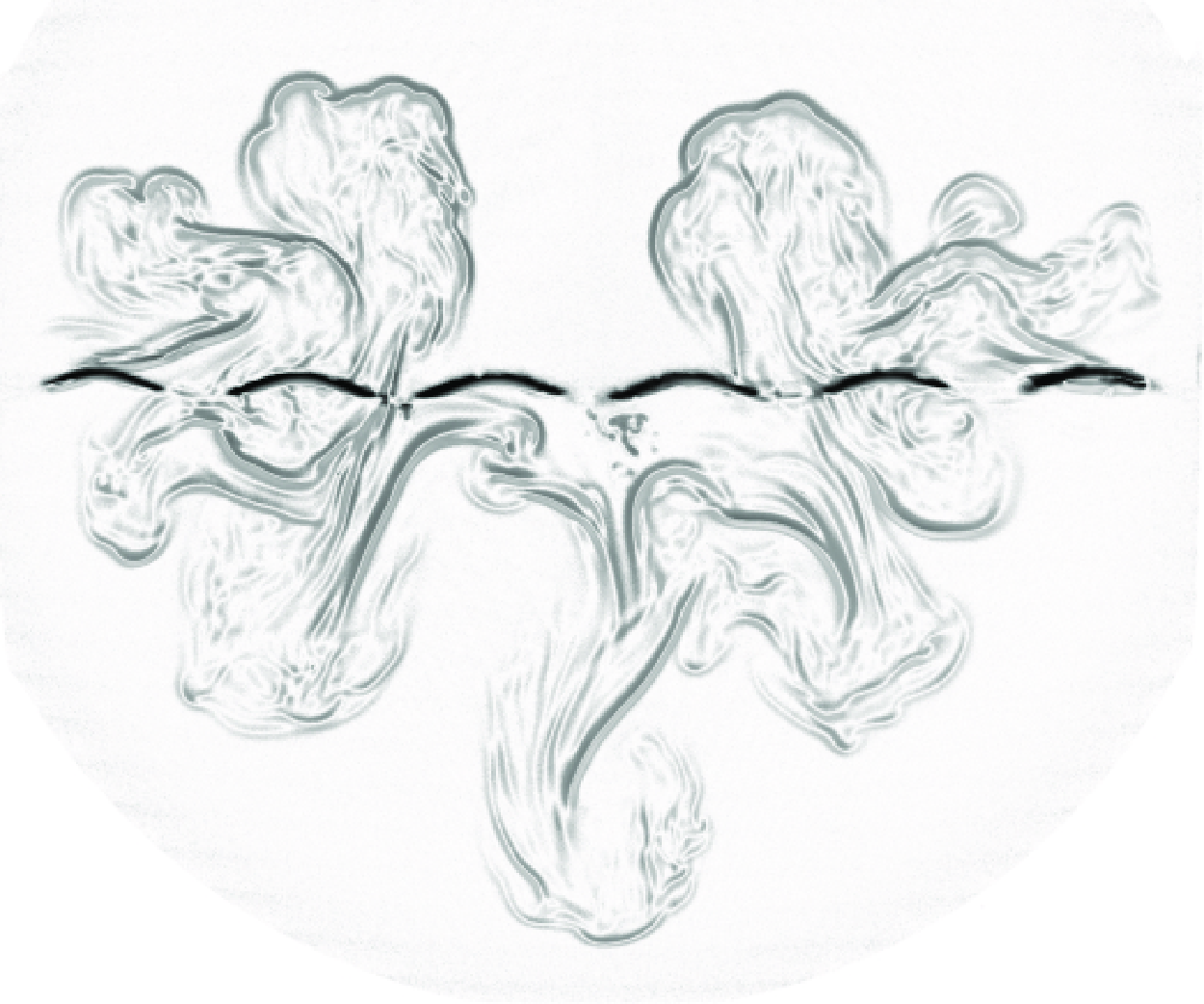
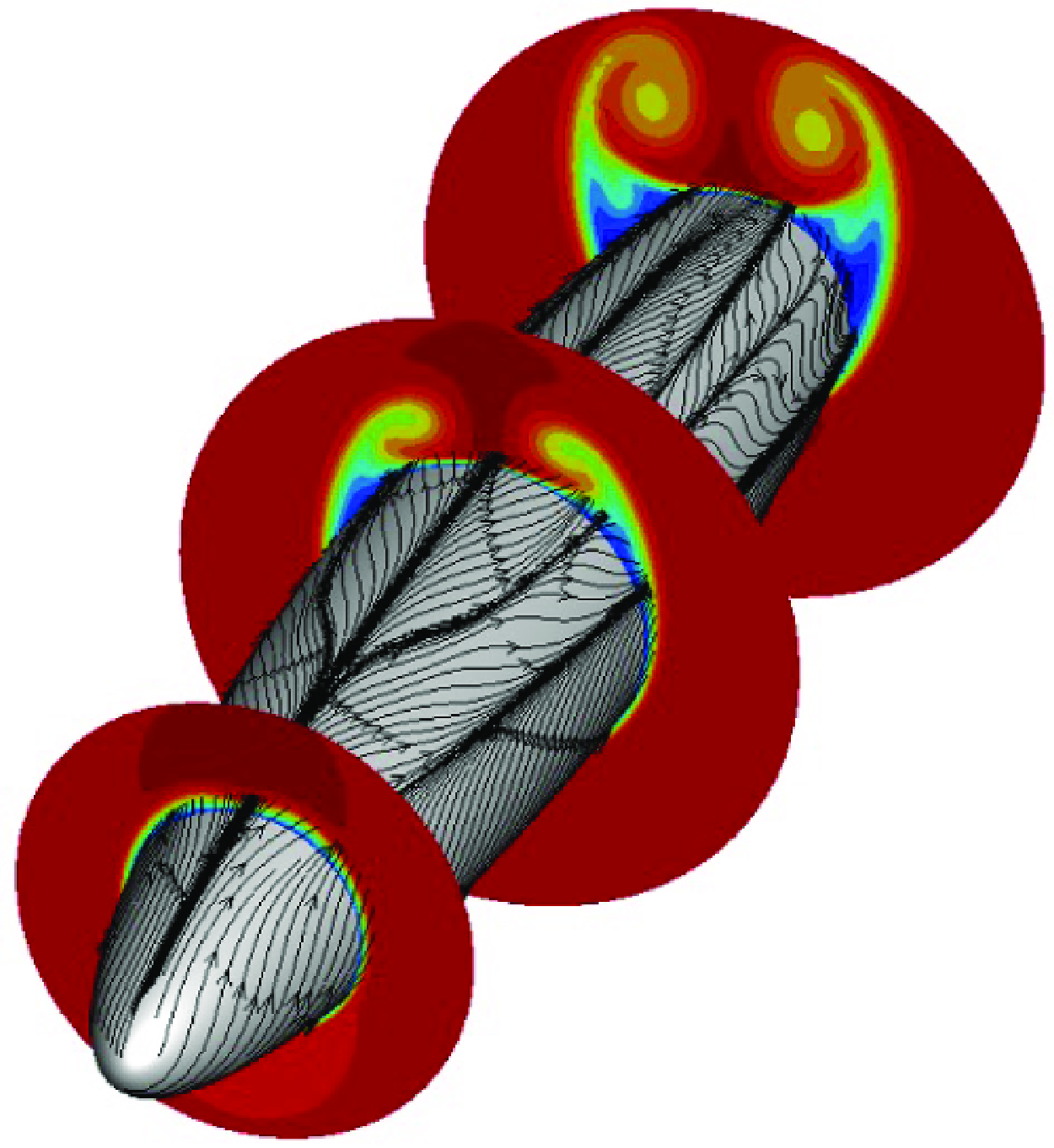
Evolution of a family of vortex rings with zero circulation
-
- Journal:
- Journal of Fluid Mechanics / Volume 1015 / 25 July 2025
- Published online by Cambridge University Press:
- 17 July 2025, A29
-
- Article
- Export citation
Handling of model uncertainties for underdetermined gas path analysis
-
- Journal:
- The Aeronautical Journal / Volume 129 / Issue 1338 / August 2025
- Published online by Cambridge University Press:
- 17 July 2025, pp. 2263-2282
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Beam steering and cross-polarization decoupling enhancement for 4 × 4 microstrip antenna arrays with differential evolution
-
- Journal:
- International Journal of Microwave and Wireless Technologies / Volume 17 / Issue 5 / June 2025
- Published online by Cambridge University Press:
- 17 July 2025, pp. 774-783
-
- Article
- Export citation
1 - Preface
-
- Book:
- Financial Data Science
- Published online:
- 17 December 2025
- Print publication:
- 17 July 2025, pp 1-6
-
- Chapter
- Export citation
Index
-
- Book:
- Financial Data Science
- Published online:
- 17 December 2025
- Print publication:
- 17 July 2025, pp 397-400
-
- Chapter
- Export citation
Thermoviscous localisation of volcanic eruptions is enhanced by variations in fissure width
-
- Journal:
- Journal of Fluid Mechanics / Volume 1015 / 25 July 2025
- Published online by Cambridge University Press:
- 17 July 2025, A18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Interaction of a vortex ring with a buoyant spherical particle: effects of particle size on vorticity dynamics and particle dynamics
-
- Journal:
- Journal of Fluid Mechanics / Volume 1015 / 25 July 2025
- Published online by Cambridge University Press:
- 17 July 2025, A24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Experimental investigation of two-dimensional Rayleigh–Taylor instability with controllable initial conditions
-
- Journal:
- Journal of Fluid Mechanics / Volume 1015 / 25 July 2025
- Published online by Cambridge University Press:
- 17 July 2025, A10
-
- Article
- Export citation
Dedication
-
- Book:
- Financial Data Science
- Published online:
- 17 December 2025
- Print publication:
- 17 July 2025, pp v-vi
-
- Chapter
- Export citation
New insights into the cavitation erosion by bubble collapse at moderate stand-off distances
-
- Journal:
- Journal of Fluid Mechanics / Volume 1015 / 25 July 2025
- Published online by Cambridge University Press:
- 17 July 2025, A33
-
- Article
- Export citation
9 - Neural networks and deep learning
-
- Book:
- Financial Data Science
- Published online:
- 17 December 2025
- Print publication:
- 17 July 2025, pp 215-244
-
- Chapter
- Export citation
7 - Linear classifiers
-
- Book:
- Financial Data Science
- Published online:
- 17 December 2025
- Print publication:
- 17 July 2025, pp 165-192
-
- Chapter
- Export citation
Copyright page
-
- Book:
- Financial Data Science
- Published online:
- 17 December 2025
- Print publication:
- 17 July 2025, pp iv-iv
-
- Chapter
- Export citation

Fundamentals of Electrical Engineering
-
- Published online:
- 16 July 2025
- Print publication:
- 10 November 2016
-
- Textbook
- Export citation
Enstrophy variations in the collapsing process of point vortices
-
- Journal:
- Journal of Fluid Mechanics / Volume 1015 / 25 July 2025
- Published online by Cambridge University Press:
- 16 July 2025, A14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Heat transfer in drop-laden low-Prandtl-number channel turbulence
-
- Journal:
- Journal of Fluid Mechanics / Volume 1015 / 25 July 2025
- Published online by Cambridge University Press:
- 16 July 2025, A19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
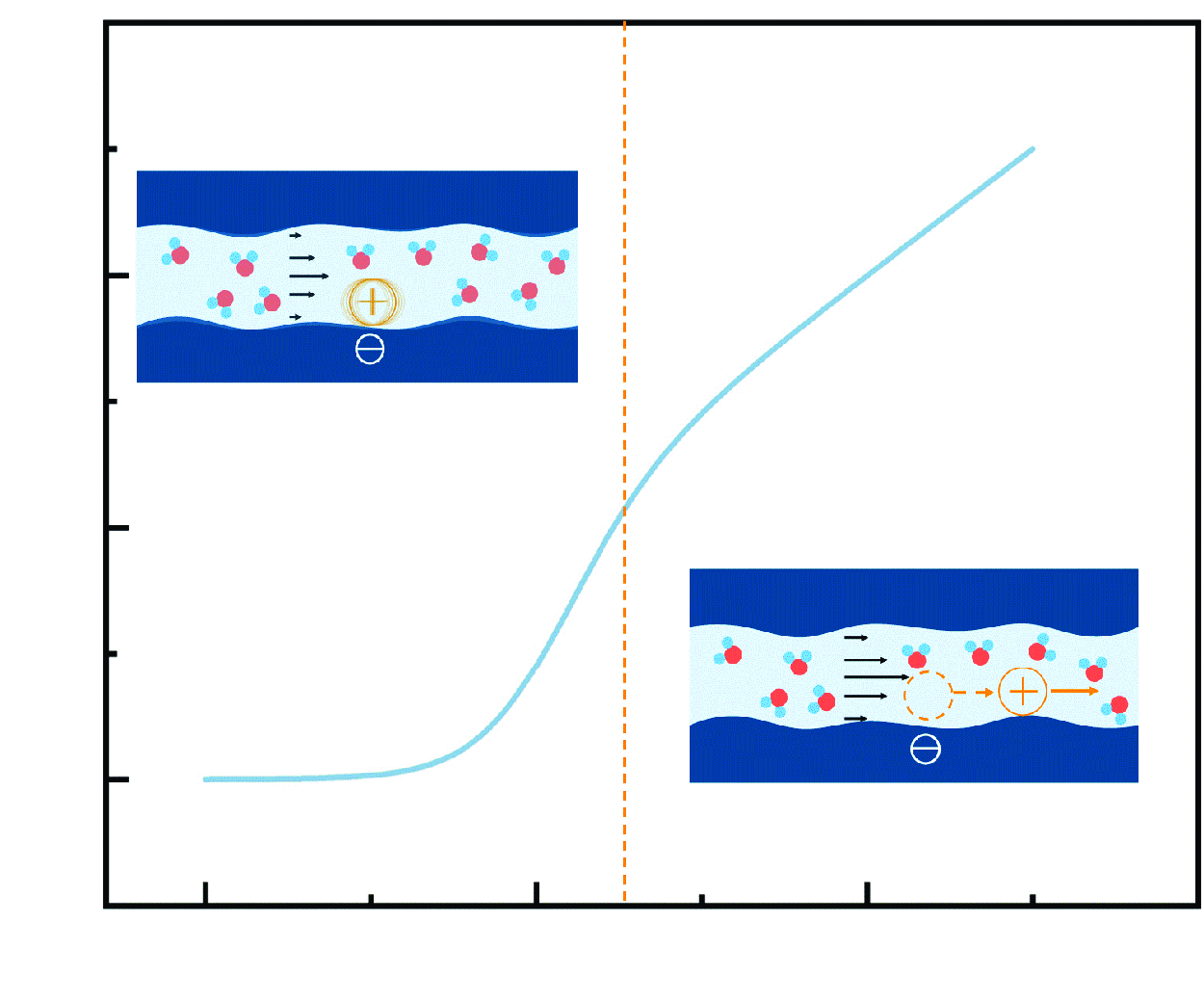
Angstrom-scale ionic streaming when the electrical double-layer concept fails
-
- Journal:
- Journal of Fluid Mechanics / Volume 1015 / 25 July 2025
- Published online by Cambridge University Press:
- 16 July 2025, A13
-
- Article
- Export citation
Vorticity dynamics and drag for flows over a sphere and a prolate spheroid
-
- Journal:
- Journal of Fluid Mechanics / Volume 1015 / 25 July 2025
- Published online by Cambridge University Press:
- 16 July 2025, A9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Interactions of flexural-gravity and interfacial waves in a two-layer fluid with a discontinuous background mean flow
-
- Journal:
- Journal of Fluid Mechanics / Volume 1015 / 25 July 2025
- Published online by Cambridge University Press:
- 16 July 2025, A22
-
- Article
- Export citation
Flow-induced vibration of a cylinder subjected to proximity interference by a downstream-cylinder
-
- Journal:
- Journal of Fluid Mechanics / Volume 1015 / 25 July 2025
- Published online by Cambridge University Press:
- 16 July 2025, A16
-
- Article
- Export citation