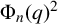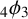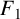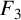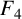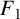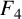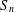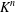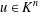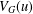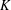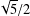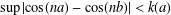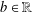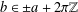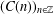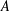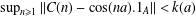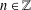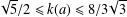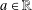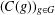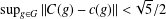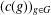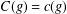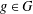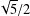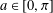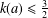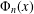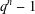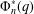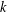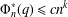Refine search
Actions for selected content:
13 results
CONGRUENCES FOR SUMS OF MACMAHON’S q-CATALAN POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 08 October 2024, pp. 416-427
- Print publication:
- June 2025
-
- Article
- Export citation
A q-SUPERCONGRUENCE ARISING FROM ANDREWS’
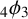 $_4\phi _3$ IDENTITY
$_4\phi _3$ IDENTITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 29 August 2024, pp. 223-227
- Print publication:
- April 2025
-
- Article
- Export citation
NEW CONGRUENCES FOR THE TRUNCATED APPELL SERIES
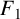 $F_1$
$F_1$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 18 April 2024, pp. 146-153
- Print publication:
- February 2025
-
- Article
- Export citation
ON THE DIVISIBILITY OF SUMS OF q-SUPER CATALAN NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 15 May 2023, pp. 215-224
- Print publication:
- April 2024
-
- Article
- Export citation
A GENERALISATION OF A SUPERCONGRUENCE ON THE TRUNCATED APPELL SERIES
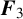 $\boldsymbol F_3$
$\boldsymbol F_3$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 13 July 2022, pp. 296-303
- Print publication:
- April 2023
-
- Article
- Export citation
A FAMILY OF
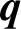 $\boldsymbol {q}$-SUPERCONGRUENCES MODULO THE CUBE OF A CYCLOTOMIC POLYNOMIAL
$\boldsymbol {q}$-SUPERCONGRUENCES MODULO THE CUBE OF A CYCLOTOMIC POLYNOMIAL
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 03 September 2021, pp. 296-302
- Print publication:
- April 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A
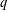 $q$-ANALOGUE OF A DWORK-TYPE SUPERCONGRUENCE
$q$-ANALOGUE OF A DWORK-TYPE SUPERCONGRUENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 17 July 2020, pp. 303-310
- Print publication:
- April 2021
-
- Article
- Export citation
PROOF OF TWO CONJECTURES ON SUPERCONGRUENCES INVOLVING CENTRAL BINOMIAL COEFFICIENTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 13 February 2020, pp. 360-364
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
A
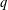 $q$-ANALOGUE OF A HYPERGEOMETRIC CONGRUENCE
$q$-ANALOGUE OF A HYPERGEOMETRIC CONGRUENCE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 294-298
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
ON THE DIMENSION OF PERMUTATION VECTOR SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 03 April 2019, pp. 256-267
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
A ZERO-
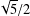 $\!\sqrt{5}/2$ LAW FOR COSINE FAMILIES
$\!\sqrt{5}/2$ LAW FOR COSINE FAMILIES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 17 April 2017, pp. 195-217
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
PRIMITIVE PRIME DIVISORS AND THE
 $\mathbf{n}$ TH CYCLOTOMIC POLYNOMIAL
$\mathbf{n}$ TH CYCLOTOMIC POLYNOMIAL
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 102 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 04 November 2015, pp. 122-135
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
Resultants of Chebyshev Polynomials: the First, Second, Third, and Fourth Kinds
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 2 / 01 June 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 423-431
- Print publication:
- 01 June 2015
-
- Article
-
- You have access
- Export citation