No CrossRef data available.
Article contents
ON THE DIMENSION OF PERMUTATION VECTOR SPACES
Part of:
Finite fields and commutative rings (number-theoretic aspects)
Permutation groups
Basic linear algebra
Published online by Cambridge University Press: 03 April 2019
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let 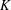 $K$ be a field that admits a cyclic Galois extension of degree
$K$ be a field that admits a cyclic Galois extension of degree 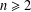 $n\geq 2$. The symmetric group
$n\geq 2$. The symmetric group 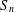 $S_{n}$ acts on
$S_{n}$ acts on 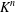 $K^{n}$ by permutation of coordinates. Given a subgroup
$K^{n}$ by permutation of coordinates. Given a subgroup 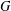 $G$ of
$G$ of 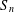 $S_{n}$ and
$S_{n}$ and 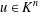 $u\in K^{n}$, let
$u\in K^{n}$, let 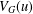 $V_{G}(u)$ be the
$V_{G}(u)$ be the 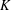 $K$-vector space spanned by the orbit of
$K$-vector space spanned by the orbit of  $u$ under the action of
$u$ under the action of 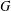 $G$. In this paper we show that, for a special family of groups
$G$. In this paper we show that, for a special family of groups 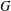 $G$ of affine type, the dimension of
$G$ of affine type, the dimension of 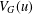 $V_{G}(u)$ can be computed via the greatest common divisor of certain polynomials in
$V_{G}(u)$ can be computed via the greatest common divisor of certain polynomials in 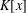 $K[x]$. We present some applications of our results to the cases
$K[x]$. We present some applications of our results to the cases 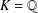 $K=\mathbb{Q}$ and
$K=\mathbb{Q}$ and 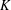 $K$ finite.
$K$ finite.
MSC classification
Primary:
11T06: Polynomials
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 100 , Issue 2 , October 2019 , pp. 256 - 267
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
Footnotes
The author was supported by FAPESP Brazil, grant no. 2018/03038-2.
References
Artin, E., Galois Theory, Notre Dame Mathematical Lectures, 2 (University of Notre Dame, Notre Dame, IN, 1942).Google Scholar
Lidl, R. and Niederreiter, H., Introduction to Finite Fields and Their Applications (Cambridge University Press, New York, 1986).Google Scholar
Pomerance, C., Thompson, L. and Weingartner, A., ‘On integers n for which x
n
- 1 has a divisor of every degree’, Acta Arith.
175 (2016), 225–243.Google Scholar

