No CrossRef data available.
Article contents
A ZERO- 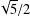 $\!\sqrt{5}/2$ LAW FOR COSINE FAMILIES
$\!\sqrt{5}/2$ LAW FOR COSINE FAMILIES
Published online by Cambridge University Press: 17 April 2017
Abstract
Let 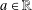 $a\in \mathbb{R}$ , and let
$a\in \mathbb{R}$ , and let 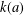 $k(a)$ be the largest constant such that
$k(a)$ be the largest constant such that 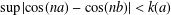 $\sup |\text{cos}(na)-\cos (nb)|<k(a)$ for
$\sup |\text{cos}(na)-\cos (nb)|<k(a)$ for 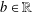 $b\in \mathbb{R}$ implies that
$b\in \mathbb{R}$ implies that 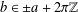 $b\in \pm a+2\unicode[STIX]{x1D70B}\mathbb{Z}$ . We show that if a cosine sequence
$b\in \pm a+2\unicode[STIX]{x1D70B}\mathbb{Z}$ . We show that if a cosine sequence 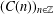 $(C(n))_{n\in \mathbb{Z}}$ with values in a Banach algebra
$(C(n))_{n\in \mathbb{Z}}$ with values in a Banach algebra 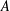 $A$ satisfies
$A$ satisfies 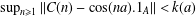 $\sup _{n\geq 1}\Vert C(n)-\cos (na).1_{A}\Vert <k(a)$ , then
$\sup _{n\geq 1}\Vert C(n)-\cos (na).1_{A}\Vert <k(a)$ , then 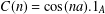 $C(n)=\cos (na).1_{A}$ for
$C(n)=\cos (na).1_{A}$ for 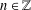 $n\in \mathbb{Z}$ . Since
$n\in \mathbb{Z}$ . Since  $\!\sqrt{5}/2\leq k(a)\leq 8/3\!\sqrt{3}$ for every
$\!\sqrt{5}/2\leq k(a)\leq 8/3\!\sqrt{3}$ for every 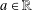 $a\in \mathbb{R}$ , this shows that if some cosine family
$a\in \mathbb{R}$ , this shows that if some cosine family 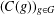 $(C(g))_{g\in G}$ over an abelian group
$(C(g))_{g\in G}$ over an abelian group 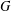 $G$ in a Banach algebra satisfies
$G$ in a Banach algebra satisfies 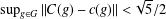 $\sup _{g\in G}\Vert C(g)-c(g)\Vert <\!\sqrt{5}/2$ for some scalar cosine family
$\sup _{g\in G}\Vert C(g)-c(g)\Vert <\!\sqrt{5}/2$ for some scalar cosine family 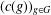 $(c(g))_{g\in G}$ , then
$(c(g))_{g\in G}$ , then  $C(g)=c(g)$ for
$C(g)=c(g)$ for  $g\in G$ , and the constant
$g\in G$ , and the constant 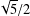 $\!\sqrt{5}/2$ is optimal. We also describe the set of all real numbers
$\!\sqrt{5}/2$ is optimal. We also describe the set of all real numbers 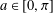 $a\in [0,\unicode[STIX]{x1D70B}]$ satisfying
$a\in [0,\unicode[STIX]{x1D70B}]$ satisfying 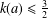 $k(a)\leq \frac{3}{2}$ .
$k(a)\leq \frac{3}{2}$ .
Keywords
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2017 Australian Mathematical Publishing Association Inc.

