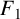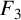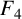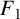Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Wang, Xiaoxia
and
Yu, Wenjie
2025.
More supercongruences for the truncated Appell series $$F_{1}$$ and $$F_{4}$$.
The Ramanujan Journal,
Vol. 68,
Issue. 2,
Wang, Xiaoxia
and
Yu, Wenjie
2026.
Some new supercongruences on the truncated Appell series F3.
Journal of Mathematical Analysis and Applications,
Vol. 556,
Issue. 1,
p.
130107.
He, Haihong
and
Wang, Xiaoxia
2026.
q-supercongruences for truncated q-Appell series.
Advances in Applied Mathematics,
Vol. 172,
Issue. ,
p.
102961.