Refine search
Actions for selected content:
35 results
NONCOMMUTATIVE IWASAWA THEORY OF ABELIAN VARIETIES OVER GLOBAL FUNCTION FIELDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 01 December 2025, pp. 1-35
-
- Article
- Export citation
An asymptotic formula for Tate–Shafarevich groups of CM elliptic curves at supersingular primes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 13 November 2025, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the
 $\mu$-invariant of two-variable
$\mu$-invariant of two-variable  $2$-adic
$2$-adic  $\boldsymbol{L}$-functions
$\boldsymbol{L}$-functions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 325-355
- Print publication:
- September 2025
-
- Article
- Export citation
A bound on the
 $\mu $-invariants of supersingular elliptic curves
$\mu $-invariants of supersingular elliptic curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 07 February 2025, pp. 787-796
- Print publication:
- September 2025
-
- Article
- Export citation
Rarity of pseudo-null Iwasawa modules for p-adic Lie extensions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 10 January 2025, pp. 709-724
- Print publication:
- September 2025
-
- Article
- Export citation
Kato’s main conjecture for potentially ordinary primes
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 26 January 2024, pp. 338-358
- Print publication:
- May 2024
-
- Article
- Export citation
THE DIAGONAL CYCLE EULER SYSTEM FOR
 $\mathrm {GL}_2\times \mathrm {GL}_2$
$\mathrm {GL}_2\times \mathrm {GL}_2$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 13 June 2023, pp. 1591-1653
- Print publication:
- September 2025
-
- Article
- Export citation
REMARKS ON HILBERT’S TENTH PROBLEM AND THE IWASAWA THEORY OF ELLIPTIC CURVES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 30 August 2022, pp. 440-450
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Growth of Fine Selmer Groups in Infinite Towers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 13 March 2020, pp. 921-936
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
Congruences with Eisenstein series and
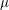 $\unicode[STIX]{x1D707}$-invariants
$\unicode[STIX]{x1D707}$-invariants
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 5 / May 2019
- Published online by Cambridge University Press:
- 10 April 2019, pp. 863-901
- Print publication:
- May 2019
-
- Article
- Export citation
A Generalization of a Theorem of Swan with Applications to Iwasawa Theory
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 72 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 16 November 2018, pp. 656-675
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
A Note on p-adic Rankin–Selberg L-functions
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 3 / 01 September 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 608-621
- Print publication:
- 01 September 2018
-
- Article
-
- You have access
- Export citation
Growth of
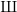 $\unicode[STIX]{x0428}$ in towers for isogenous curves
$\unicode[STIX]{x0428}$ in towers for isogenous curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 11 / November 2015
- Published online by Cambridge University Press:
- 30 June 2015, pp. 1981-2005
- Print publication:
- November 2015
-
- Article
- Export citation
Selmer groups and class groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 3 / March 2015
- Published online by Cambridge University Press:
- 11 November 2014, pp. 416-434
- Print publication:
- March 2015
-
- Article
- Export citation
HIGHER ORDER CONGRUENCES AMONGST HASSE–WEIL
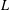 $L$-VALUES
$L$-VALUES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 98 / Issue 1 / February 2015
- Published online by Cambridge University Press:
- 14 October 2014, pp. 1-38
- Print publication:
- February 2015
-
- Article
-
- You have access
- Export citation
Signed-Selmer Groups over the ℤ2p-extension of an Imaginary Quadratic Field
-
- Journal:
- Canadian Journal of Mathematics / Volume 66 / Issue 4 / 01 August 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 826-843
- Print publication:
- 01 August 2014
-
- Article
-
- You have access
- Export citation
On λ-invariants of number fields and étale cohomology
-
- Journal:
- Journal of K-Theory / Volume 12 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 05 July 2013, pp. 167-181
- Print publication:
- August 2013
-
- Article
- Export citation
THE PLUS/MINUS SELMER GROUPS FOR SUPERSINGULAR PRIMES
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 95 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 07 June 2013, pp. 189-200
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
Iwasawa Theory for K2n
-
- Journal:
- Journal of K-Theory / Volume 12 / Issue 1 / August 2013
- Published online by Cambridge University Press:
- 02 May 2013, pp. 115-123
- Print publication:
- August 2013
-
- Article
- Export citation
On the Dihedral Main Conjectures of Iwasawa Theory for Hilbert Modular Eigenforms
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 2 / 01 April 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 403-466
- Print publication:
- 01 April 2013
-
- Article
-
- You have access
- Export citation





















 .
.


































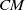

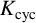
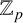
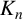
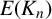
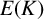
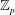

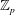
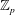
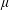

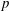
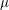
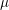
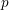
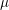
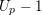
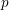
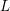
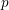
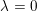








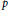

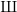
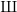
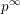
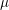
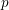
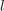
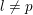
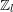
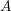
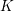
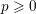
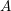
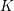
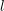
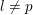
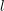
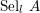
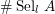
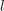
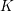
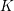
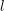
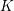
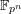
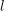
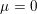
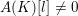
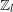
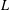
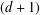
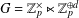
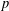
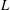
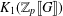
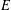
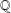
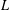
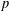









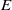
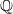
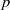
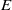
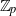
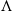
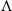

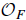
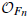 denote its ring of integers. We establish an analogue of the classical Iwasawa theorem for the orders of
denote its ring of integers. We establish an analogue of the classical Iwasawa theorem for the orders of