Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lim, Meng Fai
2022.
On the growth of even K-groups of rings of integers in p-adic Lie extensions.
Israel Journal of Mathematics,
Vol. 249,
Issue. 2,
p.
735.
Lim, Meng Fai
2024.
On pj-rank of Even K-groups of Rings of Integers.
Acta Mathematica Sinica, English Series,
Vol. 40,
Issue. 10,
p.
2481.

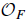
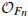 denote its ring of integers. We establish an analogue of the classical Iwasawa theorem for the orders of
denote its ring of integers. We establish an analogue of the classical Iwasawa theorem for the orders of 