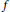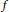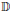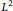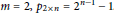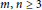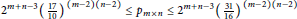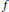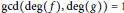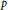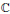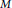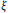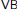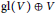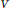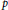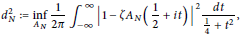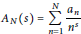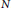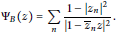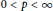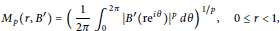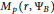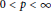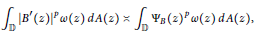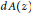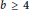Contents
Research Article
Strongly Extreme Points and Approximation Properties
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 449-457
-
- Article
-
- You have access
- Export citation
Global Holomorphic Functions in Several Non-Commuting Variables II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 458-463
-
- Article
-
- You have access
- Export citation
A Short Proof of the Characterization of Model Sets by Almost Automorphy
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 464-472
-
- Article
-
- You have access
- Export citation
A Spectral Identity on Jacobi Polynomials and its Analytic Implications
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 473-482
-
- Article
-
- You have access
- Export citation
Tannakian Duality for Affine Homogeneous Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 483-494
-
- Article
-
- You have access
- Export citation
Poincaré Lemma on Quaternion-like Heisenberg Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 495-508
-
- Article
-
- You have access
- Export citation
Area Integral Means of Analytic Functions in the Unit Disk
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 509-517
-
- Article
-
- You have access
- Export citation
Bounds on Multiple Self-avoiding Polygons
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 518-530
-
- Article
-
- You have access
- Export citation
p-adic Uniformization and the Action of Galois on Certain Affine Correspondences
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 531-542
-
- Article
-
- You have access
- Export citation
Lie Derivatives and Ricci Tensor on Real Hypersurfaces in Complex Two-plane Grassmannians
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 543-552
-
- Article
-
- You have access
- Export citation
Branching Rules for n-fold Covering Groups of SL2 over a Non-Archimedean Local Field
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 553-571
-
- Article
-
- You have access
- Export citation
Normalization of Closed Ekedahl—Oort Strata
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 572-587
-
- Article
-
- You have access
- Export citation
VB-Courant Algebroids, E-Courant Algebroids and Generalized Geometry
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 588-607
-
- Article
-
- You have access
- Export citation
A Note on p-adic Rankin–Selberg L-functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 608-621
-
- Article
-
- You have access
- Export citation
On the Size of an Expression in the Nyman–Beurling-Báez–Duarte Criterion for the Riemann Hypothesis
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 622-627
-
- Article
-
- You have access
- Export citation
Differential-free Characterisation of Smooth Mappings with Controlled Growth
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 628-636
-
- Article
-
- You have access
- Export citation
Uniformization and Steinness
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 637-639
-
- Article
-
- You have access
- Export citation
Remark on Integral Means of Derivatives of Blaschke Products
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 640-649
-
- Article
-
- You have access
- Export citation
Connected Numbers and the Embedded Topology of Plane Curves
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 650-658
-
- Article
-
- You have access
- Export citation
On Deformations of Nodal Hypersurfaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 659-672
-
- Article
-
- You have access
- Export citation