Hostname: page-component-7dd5485656-hw7sx Total loading time: 0 Render date: 2025-10-29T15:57:04.824Z Has data issue: false hasContentIssue false
  • English
  • Français

Uniformization and Steinness

Published online by Cambridge University Press:  20 November 2018

Stefan Nemirovski  and
Rasul Gazimovich Shafikov
Stefan Nemirovski
Affiliation:
Steklov Mathematical Institute, Moscow, Russia and Fakultät für Mathematik, Ruhr-Universität Bochum, Germany, e-mail : stefan@mi.ras.ru
Rasul Gazimovich Shafikov
Affiliation:
Department of Mathematics, The University of Western Ontario, London ON N6A 5B7, e-mail : shafikov@uwo.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is shown that the unit ball in 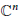${{\mathbb{C}}^{n}}$ is the only complexmanifold that can universally cover both Stein and non-Stein strictly pseudoconvex domains.

Keywords

32T1532Q30Stein manifoldcoveringspherical domain

Information

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 3 , 01 September 2018 , pp. 637 - 639
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Chirka, E. M., Complex analytic sets. Mathematics and its Applications (Soviet Series), 46, Kluwer Academic Publishers, Dordrecht, 1989. http://dx.doi.Org/10.1007/978-94-009-2366-9Google Scholar
[2] Goldman, W. M., Kapovich, M., and Leeb, B., Complex hyperbolic manifolds homotopy equivalent to a Riemann surface. Comm. Anal. Geom. 9(2001), 61–95. http://dx.doi.org/10.4310/CAC.2001.v9.n1.a3Google Scholar
[3] Forstneric, F., A complex surface admitting a strongly plurisubharmonic function but no holomorphic functions. J. Geom. Anal. 25(2015), 329–335. http://dx.doi.org/10.1007/s12220-013-9430-9Google Scholar
[4] Nemirovski, S. and Shafikov, R., Uniformization of strictly pseudoconvex domains. I. Izv. Math. 69(2005), 1189–1202. http://dx.doi.org/10.1070/IM2005v069n06ABEH002295Google Scholar
[5] Nemirovski, S. and Shafikov, R., Uniformization of strictly pseudoconvex domains. II. Izv. Math. 69(2005), 1203–1210. http://dx.doi.org/10.1070/IM2005v069n06ABEH002296Google Scholar
[6] Rosay, J.-P., Sur une caracterisation de la boule parmi les domaines de C” par son groupe d'automorphismes. Ann. Inst. Fourier (Grenoble) 29(1979), ix, 91–97.Google Scholar
[7] Wong, B., Characterization ofthe unit ball in C” by its automorphism group. Invent. Math. 41(1977), 253–257. http://dx.doi.org/10.1007/BF01403050Google Scholar