Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Day, Stuart
and
Taheri, Ali
2018.
Semigroup asymptotics, the Funk-Hecke identity and the Gegenbauer coefficients associated with the spherical Laplacian.
Rocky Mountain Journal of Mathematics,
Vol. 48,
Issue. 3,
Awonusika, Richard Olu
2019.
Maclaurin Heat Coefficients and Associated Zeta Functions on Quaternionic Projective Spaces Pn(H) (n ≥ 1).
Journal of Physics: Conference Series,
Vol. 1366,
Issue. 1,
p.
012055.
Awonusika, Richard Olu
2019.
On spectral identities involving Gegenbauer polynomials.
The Journal of Analysis,
Vol. 27,
Issue. 4,
p.
1123.
Awonusika, Richard Olu
2020.
Generalised heat coefficients and associated spectral zeta functions on complex projective spaces Pn(ℂ).
Complex Variables and Elliptic Equations,
Vol. 65,
Issue. 4,
p.
588.
Awonusika, Richard Olu
2021.
On Jacobi polynomials $${\mathscr {P}}_{k}^{(\alpha ,\beta )}$$ and coefficients $$c_{j}^{\ell }(\alpha ,\beta )$$ $$\left( k\ge 0, \ell =5,6; 1\le j\le \ell ; \alpha ,\beta > -1\right)$$.
The Journal of Analysis,
Vol. 29,
Issue. 3,
p.
649.
Awonusika, Richard Olu
2021.
On Jacobi polynomials and fractional spectral functions on compact symmetric spaces.
The Journal of Analysis,
Vol. 29,
Issue. 3,
p.
987.
Awonusika, Richard Olu
2022.
Maclaurin spectral results on rank one symmetric spaces of noncompact type.
The Journal of Analysis,
Vol. 30,
Issue. 1,
p.
285.
Awonusika, Richard Olu
and
Ariwayo, Afolabi Gabriel
2022.
Descriptions of fractional coefficients of Jacobi polynomial expansions.
The Journal of Analysis,
Vol. 30,
Issue. 4,
p.
1567.
Awonusika, Richard Olu
2024.
Analytical solution of a class of Lane–Emden equations: Adomian decomposition method.
The Journal of Analysis,
Vol. 32,
Issue. 2,
p.
1009.
De Micheli, Enrico
2025.
On the Integral Representation of Jacobi Polynomials.
Mathematics,
Vol. 13,
Issue. 3,
p.
483.
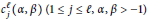 $c_{j}^{\ell }\left( \alpha ,\,\beta\right)\,\left( 1\,\le \,j\,\le \,\ell ,\,\alpha ,\,\beta \,>\,-1 \right)$ are linked to the Maclaurin spectral expansion of the Schwartz kernel of functions of the Laplacian on a compact rank one symmetric space. It is proved that these coefficients can be computed by transforming the even derivatives of the Jacobi polynomials
$c_{j}^{\ell }\left( \alpha ,\,\beta\right)\,\left( 1\,\le \,j\,\le \,\ell ,\,\alpha ,\,\beta \,>\,-1 \right)$ are linked to the Maclaurin spectral expansion of the Schwartz kernel of functions of the Laplacian on a compact rank one symmetric space. It is proved that these coefficients can be computed by transforming the even derivatives of the Jacobi polynomials 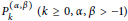 $P_{k}^{\left( \alpha ,\,\beta\right)}\,\left( k\,\ge \,0,\,\alpha ,\,\beta \,>\,-1 \right)$ into a spectral sum associated with the Jacobi operator. The first few coefficients are explicitly computed, and a direct trace interpretation of the Maclaurin coefficients is presented.
$P_{k}^{\left( \alpha ,\,\beta\right)}\,\left( k\,\ge \,0,\,\alpha ,\,\beta \,>\,-1 \right)$ into a spectral sum associated with the Jacobi operator. The first few coefficients are explicitly computed, and a direct trace interpretation of the Maclaurin coefficients is presented.
