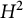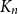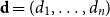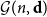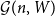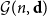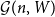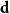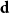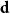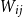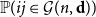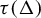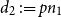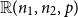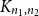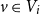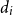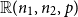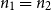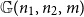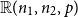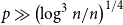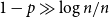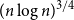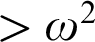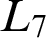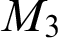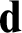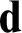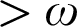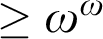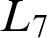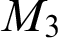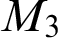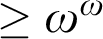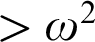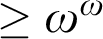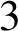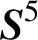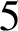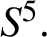Refine search
Actions for selected content:
44 results
4 - Application of Embedding Technology in Recommender Systems
-
- Book:
- Deep Learning Recommender Systems
- Published online:
- 08 May 2025
- Print publication:
- 22 May 2025, pp 117-142
-
- Chapter
- Export citation

Deep Learning Recommender Systems
-
- Published online:
- 08 May 2025
- Print publication:
- 22 May 2025
Hanging Topic Left Dislocations in seemingly embedded contexts: An English–Spanish asymmetry
-
- Journal:
- Journal of Linguistics , First View
- Published online by Cambridge University Press:
- 20 March 2025, pp. 1-12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COUNTABLY COMPACT EXTENSIONS AND CARDINAL CHARACTERISTICS OF THE CONTINUUM
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 13 February 2025, pp. 1-27
-
- Article
- Export citation
5 - Kingman Combinatorics and Shift-Compactness
-
- Book:
- Category and Measure
- Published online:
- 14 January 2025
- Print publication:
- 23 January 2025, pp 78-85
-
- Chapter
- Export citation
Embedding of some classes of operators into strongly continuous semigroups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 219-231
- Print publication:
- March 2025
-
- Article
- Export citation
Tree universality in positional games
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 3 / May 2025
- Published online by Cambridge University Press:
- 13 December 2024, pp. 338-358
-
- Article
- Export citation
Embedding theorems for random graphs with specified degrees
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 34 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 16 October 2024, pp. 115-130
-
- Article
- Export citation
Chapter 16 - Machine learning
- from Part II - Applications, tools, and tasks
-
- Book:
- Working with Network Data
- Published online:
- 06 June 2024
- Print publication:
- 13 June 2024, pp 251-278
-
- Chapter
- Export citation
COMPLETE EMBEDDINGS OF GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 26 January 2024, pp. 136-144
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
4 - The Grammar of Experiential Meaning in Korean: transitivity
-
- Book:
- Korean Grammar
- Published online:
- 16 March 2023
- Print publication:
- 23 March 2023, pp 180-276
-
- Chapter
- Export citation
Factivity and complementizer omission in English embedded gapping
-
- Journal:
- Journal of Linguistics / Volume 59 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 13 December 2022, pp. 389-426
- Print publication:
- April 2023
-
- Article
- Export citation
6 - Equivariant Borel Conjecture
-
- Book:
- Variations on a Theme of Borel
- Published online:
- 24 November 2022
- Print publication:
- 08 December 2022, pp 186-257
-
- Chapter
- Export citation
On images of subshifts under embeddings of symbolic varieties
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 9 / September 2023
- Published online by Cambridge University Press:
- 01 August 2022, pp. 3131-3149
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sandwiching biregular random graphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 06 June 2022, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
5 - Non-finiteness as the Bridge for Process Compression
-
- Book:
- Non-Finiteness
- Published online:
- 21 April 2022
- Print publication:
- 28 April 2022, pp 122-142
-
- Chapter
- Export citation
9 - Cementochronology for Archaeologists: Experiments and Testing for an Optimized Thin-Section Preparation Protocol
- from Part II - Protocols
-
-
- Book:
- Dental Cementum in Anthropology
- Published online:
- 20 January 2022
- Print publication:
- 10 February 2022, pp 173-188
-
- Chapter
- Export citation
10 - Optimizing Preparation Protocols and Microscopy for Cementochronology
- from Part II - Protocols
-
-
- Book:
- Dental Cementum in Anthropology
- Published online:
- 20 January 2022
- Print publication:
- 10 February 2022, pp 189-200
-
- Chapter
- Export citation
Towards Finding a Lattice that Characterizes the
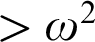 ${>}\ \omega ^2$-Fickle Recursively Enumerable Turing Degrees
${>}\ \omega ^2$-Fickle Recursively Enumerable Turing Degrees
- Part of
-
- Journal:
- Bulletin of Symbolic Logic / Volume 27 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 28 February 2022, p. 528
- Print publication:
- December 2021
-
- Article
-
- You have access
- Export citation
A NOTE ON OPEN BOOK EMBEDDINGS OF
 $3$-MANIFOLDS IN
$3$-MANIFOLDS IN 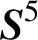 $\boldsymbol {S}^5$
$\boldsymbol {S}^5$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 04 October 2021, pp. 499-506
- Print publication:
- June 2022
-
- Article
- Export citation