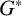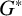1 Introduction
In 1971, Miller and Schupp [Reference Miller and Schupp14] used small cancellation theory to prove that every countable group G can be embedded in a finitely generated group
![]() $G^*$
that is hopfian and complete (asymmetric). They construct
$G^*$
that is hopfian and complete (asymmetric). They construct
![]() $G^*$
as a quotient of a free product
$G^*$
as a quotient of a free product
![]() ${G\ast U(p,q)}$
, where
${G\ast U(p,q)}$
, where
![]() $U(p,q)$
is a free product of finite cyclic groups. In particular, each of the enveloping groups that they construct has torsion. The purpose of this note is to present an alternative construction of
$U(p,q)$
is a free product of finite cyclic groups. In particular, each of the enveloping groups that they construct has torsion. The purpose of this note is to present an alternative construction of
![]() $G^*$
that does not introduce torsion. It also preserves finiteness properties of G.
$G^*$
that does not introduce torsion. It also preserves finiteness properties of G.
Theorem A. Every countable group G can be embedded in a finitely generated group
![]() $G^*$
such that:
$G^*$
such that:
-
(1)
 $G^*$
is hopfian and complete;
$G^*$
is hopfian and complete; -
(2) every finite subgroup of
 $G^*$
is conjugate to a finite subgroup of G;
$G^*$
is conjugate to a finite subgroup of G; -
(3) if G has a finite presentation (respectively, a finite classifying space of dimension
 $d\ge 3$
), then so does
$d\ge 3$
), then so does
 $G^*$
.
$G^*$
.
Our construction of
![]() $G^*$
is more explicit than that of Miller and Schupp. It is nontrivial in that it relies on the existence of asymmetric hyperbolic groups with additional properties, but the basic idea behind it is straightforward: after some gentle preparation, we are able to assume that G is generated by two finitely generated free subgroups
$G^*$
is more explicit than that of Miller and Schupp. It is nontrivial in that it relies on the existence of asymmetric hyperbolic groups with additional properties, but the basic idea behind it is straightforward: after some gentle preparation, we are able to assume that G is generated by two finitely generated free subgroups
![]() $F_1,F_2<G$
; we then rigidify G by attaching certain complete (asymmetric) groups
$F_1,F_2<G$
; we then rigidify G by attaching certain complete (asymmetric) groups
![]() $A_1$
and
$A_1$
and
![]() $A_2$
to it along
$A_2$
to it along
![]() $F_1$
and
$F_1$
and
![]() $F_2$
; the groups
$F_2$
; the groups
![]() $A_i$
are constructed so that any epimorphism
$A_i$
are constructed so that any epimorphism
![]() $\psi $
of the resulting amalgam
$\psi $
of the resulting amalgam
![]() $G^*$
must preserve the decomposition
$G^*$
must preserve the decomposition
![]() ${G^* = A_1\ast _{F_1} G \ast _{F_2} A_2}$
, sending each
${G^* = A_1\ast _{F_1} G \ast _{F_2} A_2}$
, sending each
![]() $A_i$
to itself; by ensuring that the
$A_i$
to itself; by ensuring that the
![]() $A_i$
are hopfian, as well as complete, we force the restrictions
$A_i$
are hopfian, as well as complete, we force the restrictions
![]() $\psi {\vert }_{A_i}$
to be the identity; and since
$\psi {\vert }_{A_i}$
to be the identity; and since
![]() $G^*=\langle {A_1, A_2}\rangle $
, we conclude that
$G^*=\langle {A_1, A_2}\rangle $
, we conclude that
![]() $\psi $
is the identity.
$\psi $
is the identity.
Groups
![]() $A_i$
with the properties that we need can be found among the fundamental groups of closed hyperbolic 3-manifolds obtained by Dehn surgery on the knots shown in Figure 1, as we shall explain.
$A_i$
with the properties that we need can be found among the fundamental groups of closed hyperbolic 3-manifolds obtained by Dehn surgery on the knots shown in Figure 1, as we shall explain.

Figure 1 The knots
![]() $10_{102}, 10_{106}, 10_{107}$
and
$10_{102}, 10_{106}, 10_{107}$
and
![]() $10_{110}$
.
$10_{110}$
.
2 Preliminaries
We remind the reader of some terminology. A group G is termed hopfian if every epimorphism
![]() $G\to G$
is an isomorphism, and cohopfian if every monomorphism
$G\to G$
is an isomorphism, and cohopfian if every monomorphism
![]() ${G\to G}$
is an isomorphism. G is said to be complete (or asymmetric) if it has trivial centre and every automorphism is inner. A subgroup
${G\to G}$
is an isomorphism. G is said to be complete (or asymmetric) if it has trivial centre and every automorphism is inner. A subgroup
![]() $H<G$
is malnormal if
$H<G$
is malnormal if
![]() ${H^g\cap H \neq 1}$
implies
${H^g\cap H \neq 1}$
implies
![]() $g\in H$
. A group G is said to split over a free group if G can be decomposed as an amalgamated free product
$g\in H$
. A group G is said to split over a free group if G can be decomposed as an amalgamated free product
![]() $G=A\ast _F B$
or Higman–Neumann–Neumann (HNN) extension
$G=A\ast _F B$
or Higman–Neumann–Neumann (HNN) extension
![]() $G=B\ast _F$
with F free. A group has Serre’s property
$G=B\ast _F$
with F free. A group has Serre’s property
![]() ${\mathrm {FA}}$
if it fixes a point whenever it acts on a simplicial tree.
${\mathrm {FA}}$
if it fixes a point whenever it acts on a simplicial tree.
We shall assume that the reader is familiar with the rudiments of Bass–Serre theory [Reference Serre18] and the homology of groups.
2.1 The mild preparation of G
A classical construction of B. H. Neumann embeds a countable group G in a finitely generated group
![]() $\widetilde {G}$
by means of HNN extensions and amalgamated free products (see [Reference Lyndon and Schupp12, page 188]). The finite subgroups of
$\widetilde {G}$
by means of HNN extensions and amalgamated free products (see [Reference Lyndon and Schupp12, page 188]). The finite subgroups of
![]() $\widetilde {G}$
are conjugate to subgroups of G; in particular,
$\widetilde {G}$
are conjugate to subgroups of G; in particular,
![]() $\widetilde {G}$
is torsion-free if G is torsion-free. Thus, in our attempts to construct
$\widetilde {G}$
is torsion-free if G is torsion-free. Thus, in our attempts to construct
![]() $G^*$
, there is no loss of generality in assuming that G is finitely generated.
$G^*$
, there is no loss of generality in assuming that G is finitely generated.
Replacing G by
![]() $G\ast \mathbb {Z}$
if necessary, we may also assume that our group has a generating set
$G\ast \mathbb {Z}$
if necessary, we may also assume that our group has a generating set
![]() $\{a_0,a_1,\dots ,a_n\}$
where the
$\{a_0,a_1,\dots ,a_n\}$
where the
![]() $a_i$
each have infinite order: given
$a_i$
each have infinite order: given
![]() ${G=\langle {b_1,\dots ,b_n}\rangle }$
and x generating
${G=\langle {b_1,\dots ,b_n}\rangle }$
and x generating
![]() $\mathbb {Z}$
, define
$\mathbb {Z}$
, define
![]() $a_0=x$
and
$a_0=x$
and
![]() $a_i=xb_i$
. We assume that this modification has been made. The normal-form theorem for free products then yields the following results.
$a_i=xb_i$
. We assume that this modification has been made. The normal-form theorem for free products then yields the following results.
Lemma 2.1. In
![]() $G\ast \langle {s,t}\rangle $
, the subsets
$G\ast \langle {s,t}\rangle $
, the subsets
![]() $\{s,a_0t, \dots , a_n(s^{-n}ts^n)\}$
and
$\{s,a_0t, \dots , a_n(s^{-n}ts^n)\}$
and
![]() $\{s,t,a_0t\}$
generate free subgroups of ranks
$\{s,t,a_0t\}$
generate free subgroups of ranks
![]() $n+2$
and
$n+2$
and
![]() $3$
, respectively.
$3$
, respectively.
Corollary 2.2. Replacing G by
![]() $G\ast \langle {s,t}\rangle $
if necessary, we may assume that
$G\ast \langle {s,t}\rangle $
if necessary, we may assume that
![]() ${G = \langle {F_1,F_2}\rangle }$
, where
${G = \langle {F_1,F_2}\rangle }$
, where
![]() $F_1$
and
$F_1$
and
![]() $F_2$
are finitely generated free groups with noncyclic intersection and the centraliser of
$F_2$
are finitely generated free groups with noncyclic intersection and the centraliser of
![]() $F_1\cap F_2$
in G is trivial.
$F_1\cap F_2$
in G is trivial.
2.2 Asymmetric hyperbolic manifolds
Lemma 2.3. Given integers
![]() $r>0$
and
$r>0$
and
![]() $d\ge 3$
, one can construct a complete, torsion-free, cohopfian (Gromov) hyperbolic group
$d\ge 3$
, one can construct a complete, torsion-free, cohopfian (Gromov) hyperbolic group
![]() $A(d)$
and a malnormal free subgroup
$A(d)$
and a malnormal free subgroup
![]() $L<A(d)$
of rank r such that:
$L<A(d)$
of rank r such that:
-
(1)
 $A(d)$
has a finite classifying space of dimension d;
$A(d)$
has a finite classifying space of dimension d; -
(2)
 $A(d)$
does not split over any free group; and
$A(d)$
does not split over any free group; and -
(3)
 $A(d)/\langle {\!\langle {L}\rangle \!}\rangle $
is infinite.
$A(d)/\langle {\!\langle {L}\rangle \!}\rangle $
is infinite.
Proof. By Mostow rigidity, if M is a closed orientable hyperbolic manifold of dimension
![]() $d\ge 3$
, then
$d\ge 3$
, then
![]() $\pi _1M$
is complete (asymmetric) if and only if M is asymmetric, that is, M has no nontrivial isometries. There exist such manifolds in every dimension
$\pi _1M$
is complete (asymmetric) if and only if M is asymmetric, that is, M has no nontrivial isometries. There exist such manifolds in every dimension
![]() $d\ge 3$
: Kojima [Reference Kojima10] constructed examples in dimension
$d\ge 3$
: Kojima [Reference Kojima10] constructed examples in dimension
![]() $3$
(along with manifolds that have any prescribed finite group of symmetries) and, inspired by arguments of Long and Reid [Reference Long and Reid11], Belolipetsky and Lubotzky [Reference Belilopetsky and Lubotzky1] constructed examples in each dimension
$3$
(along with manifolds that have any prescribed finite group of symmetries) and, inspired by arguments of Long and Reid [Reference Long and Reid11], Belolipetsky and Lubotzky [Reference Belilopetsky and Lubotzky1] constructed examples in each dimension
![]() $d\ge 3$
. Let M be such a d-manifold and let
$d\ge 3$
. Let M be such a d-manifold and let
![]() $A(d)=\pi _1M$
. Note that M is a classifying space for
$A(d)=\pi _1M$
. Note that M is a classifying space for
![]() $A(d)$
.
$A(d)$
.
If
![]() $A(d)$
splits nontrivially as an amalgamated free product, say
$A(d)$
splits nontrivially as an amalgamated free product, say
![]() $A(d)= D\ast _C B$
, then there is a Mayer–Vietoris exact sequence for integral homology groups
$A(d)= D\ast _C B$
, then there is a Mayer–Vietoris exact sequence for integral homology groups
By Poincaré duality,
![]() $H_dM\cong \mathbb {Z}$
and (as
$H_dM\cong \mathbb {Z}$
and (as
![]() $D, B < \pi _1M$
are of infinite index)
$D, B < \pi _1M$
are of infinite index)
![]() $H_dD = H_dB = 0$
. Thus,
$H_dD = H_dB = 0$
. Thus,
![]() $H_{d-1}C$
is infinite. In particular, since
$H_{d-1}C$
is infinite. In particular, since
![]() $d\ge 3$
, the group C cannot be free. A similar argument shows that
$d\ge 3$
, the group C cannot be free. A similar argument shows that
![]() $\pi _1M$
does not split as an HNN extension over a free group either.
$\pi _1M$
does not split as an HNN extension over a free group either.
Any subgroup of infinite index in
![]() $A(d)$
has lower cohomological dimension than
$A(d)$
has lower cohomological dimension than
![]() $A(d)$
, and a subgroup of finite index cannot be isomorphic to
$A(d)$
, and a subgroup of finite index cannot be isomorphic to
![]() $A(d)$
by Mostow rigidity. Thus,
$A(d)$
by Mostow rigidity. Thus,
![]() $A(d)$
is cohopfian.
$A(d)$
is cohopfian.
Every nonelementary hyperbolic group contains proper, normal subgroups of infinite index, and Kapovich [Reference Kapovich8] shows that inside such a subgroup one can find a malnormal free subgroup of rank
![]() $2$
, and inside that one can find a malnormal subgroup of any finite rank.
$2$
, and inside that one can find a malnormal subgroup of any finite rank.
3 The main argument
Given a countable group G, we modify it to arrive in the situation
![]() $G = \langle {F_1,F_2}\rangle $
described in Corollary 2.2. Let
$G = \langle {F_1,F_2}\rangle $
described in Corollary 2.2. Let
![]() $r_i$
be the rank of the free group
$r_i$
be the rank of the free group
![]() $F_i$
and construct groups
$F_i$
and construct groups
![]() $A_i=A(d_i)$
with malnormal free subgroups
$A_i=A(d_i)$
with malnormal free subgroups
![]() $L_i<A_i$
of rank
$L_i<A_i$
of rank
![]() $r_i$
as in Lemma 2.3. We may assume that
$r_i$
as in Lemma 2.3. We may assume that
![]() $A_1$
is not isomorphic to
$A_1$
is not isomorphic to
![]() $A_2$
(Remark 3.2). Let
$A_2$
(Remark 3.2). Let
where the amalgamation identifies
![]() $F_i< G$
with
$F_i< G$
with
![]() $L_i<A_i$
. Note that since
$L_i<A_i$
. Note that since
![]() $G=\langle {F_1,F_2}\rangle $
, we have
$G=\langle {F_1,F_2}\rangle $
, we have
![]() $G^*=\langle {A_1,A_2}\rangle $
.
$G^*=\langle {A_1,A_2}\rangle $
.
Theorem 3.1.
![]() $G^*$
is complete.
$G^*$
is complete.
Proof. The centre of
![]() $G^*$
is trivial because the centre of any amalgamated free product lies in the intersection of the edge groups, and the edge groups in the defining decomposition of
$G^*$
is trivial because the centre of any amalgamated free product lies in the intersection of the edge groups, and the edge groups in the defining decomposition of
![]() $G^*$
are centreless.
$G^*$
are centreless.
Let
![]() $\phi : G^*\to G^*$
be an automorphism; we must argue that
$\phi : G^*\to G^*$
be an automorphism; we must argue that
![]() $\phi $
is inner. As
$\phi $
is inner. As
![]() $A_i$
does not split over a free group, the action of
$A_i$
does not split over a free group, the action of
![]() $\phi (A_i)$
on the Bass–Serre tree of the given splitting of
$\phi (A_i)$
on the Bass–Serre tree of the given splitting of
![]() $G^*$
must fix a vertex. Thus, each of
$G^*$
must fix a vertex. Thus, each of
![]() $\phi (A_1)$
and
$\phi (A_1)$
and
![]() $\phi (A_2)$
is contained in a conjugate of
$\phi (A_2)$
is contained in a conjugate of
![]() $A_1, A_2$
or G.
$A_1, A_2$
or G.
We have chosen the
![]() $A_i$
so that
$A_i$
so that
![]() $Q_i:=A_i/\langle {\!\langle {F_i}\rangle \!}\rangle $
is infinite. Note that
$Q_i:=A_i/\langle {\!\langle {F_i}\rangle \!}\rangle $
is infinite. Note that
![]() $Q_1\cong G^*/\langle {\!\langle {G, A_2}\rangle \!}\rangle $
and
$Q_1\cong G^*/\langle {\!\langle {G, A_2}\rangle \!}\rangle $
and
![]() $Q_2\cong G^*/\langle {\!\langle {G, A_1}\rangle \!}\rangle $
. Thus, a pair of conjugates of
$Q_2\cong G^*/\langle {\!\langle {G, A_1}\rangle \!}\rangle $
. Thus, a pair of conjugates of
![]() $A_1, A_2$
or G can only generate
$A_1, A_2$
or G can only generate
![]() $G^*$
if one of the pair is a conjugate of
$G^*$
if one of the pair is a conjugate of
![]() $A_1$
and the other is a conjugate of
$A_1$
and the other is a conjugate of
![]() $A_2$
. If
$A_2$
. If
![]() $\phi $
maps
$\phi $
maps
![]() $A_1$
into a conjugate of
$A_1$
into a conjugate of
![]() $A_2$
, then
$A_2$
, then
![]() $\phi ^2$
would map
$\phi ^2$
would map
![]() $A_1$
to a conjugate of itself, and since
$A_1$
to a conjugate of itself, and since
![]() $A_1$
is cohopfian, the image would be the whole of this conjugate. This forces
$A_1$
is cohopfian, the image would be the whole of this conjugate. This forces
![]() $\phi (A_1)$
to be equal to the conjugate of
$\phi (A_1)$
to be equal to the conjugate of
![]() $A_2$
containing it, which is impossible since we have chosen
$A_2$
containing it, which is impossible since we have chosen
![]() $A_1$
and
$A_1$
and
![]() $A_2$
to be not isomorphic. We conclude that
$A_2$
to be not isomorphic. We conclude that
![]() $\phi $
maps
$\phi $
maps
![]() $A_i$
isomorphically onto a conjugate of itself for
$A_i$
isomorphically onto a conjugate of itself for
![]() $i=1,2$
.
$i=1,2$
.
Now, since all automorphisms of
![]() $A_1$
are assumed to be inner, we can compose
$A_1$
are assumed to be inner, we can compose
![]() $\phi $
with an inner automorphism of
$\phi $
with an inner automorphism of
![]() $G^*$
to assume that
$G^*$
to assume that
![]() $\phi {\vert }_{A_1}={\mathrm {id}}_{A_1}$
, while
$\phi {\vert }_{A_1}={\mathrm {id}}_{A_1}$
, while
![]() $\phi (A_2)=A_2^\gamma $
for some
$\phi (A_2)=A_2^\gamma $
for some
![]() $\gamma \in G^*$
.
$\gamma \in G^*$
.
Consider the Bass–Serre tree for the splitting
![]() $G^* = A_1\ast _{F_1} G\ast _{F_2} A_2.$
We refer to the vertices as being of type
$G^* = A_1\ast _{F_1} G\ast _{F_2} A_2.$
We refer to the vertices as being of type
![]() $A_1, A_2$
or G, according to whether they are in the
$A_1, A_2$
or G, according to whether they are in the
![]() $G^*$
orbit of the vertices (identity cosets)
$G^*$
orbit of the vertices (identity cosets)
![]() $A_1, A_2$
or G, respectively. Since
$A_1, A_2$
or G, respectively. Since
![]() $F_i<A_i$
is malnormal for
$F_i<A_i$
is malnormal for
![]() $i=1,2$
, no arc of length greater than
$i=1,2$
, no arc of length greater than
![]() $2$
in this tree has nontrivial stabiliser, and any arc of length
$2$
in this tree has nontrivial stabiliser, and any arc of length
![]() $2$
with nontrivial stabiliser must be centred at a vertex of type G. In particular, the subtree fixed by
$2$
with nontrivial stabiliser must be centred at a vertex of type G. In particular, the subtree fixed by
![]() $F_1\cap F_2$
, which contains the vertices
$F_1\cap F_2$
, which contains the vertices
![]() $A_1, G$
and
$A_1, G$
and
![]() $A_2$
, has diameter
$A_2$
, has diameter
![]() $2$
and centroid G. The centraliser of
$2$
and centroid G. The centraliser of
![]() $F_1\cap F_2$
in
$F_1\cap F_2$
in
![]() $G^*$
leaves this subtree and its centroid invariant, and hence is contained in G. But, by construction, the centraliser of
$G^*$
leaves this subtree and its centroid invariant, and hence is contained in G. But, by construction, the centraliser of
![]() $F_1\cap F_2$
in G is trivial, and hence so is its centraliser in
$F_1\cap F_2$
in G is trivial, and hence so is its centraliser in
![]() $G^*$
.
$G^*$
.
As
![]() $\phi (A_2)=A_2^\gamma $
, we have an isomorphism
$\phi (A_2)=A_2^\gamma $
, we have an isomorphism
![]() ${\mathrm {ad}}(\gamma )^{-1}\circ \phi {\vert }_{A_2}:A_2\to A_2$
. As
${\mathrm {ad}}(\gamma )^{-1}\circ \phi {\vert }_{A_2}:A_2\to A_2$
. As
![]() $A_2$
is complete, this isomorphism is conjugation by some
$A_2$
is complete, this isomorphism is conjugation by some
![]() $a\in A_2$
, so
$a\in A_2$
, so
![]() $\phi {\vert }_{A_2}$
is conjugation by
$\phi {\vert }_{A_2}$
is conjugation by
![]() ${\gamma a\in G^*}$
. But
${\gamma a\in G^*}$
. But
![]() $\phi $
restricts to the identity on
$\phi $
restricts to the identity on
![]() ${F_1\cap F_2}<A_2$
, and we know that the centraliser of
${F_1\cap F_2}<A_2$
, and we know that the centraliser of
![]() $F_1\cap F_2$
in
$F_1\cap F_2$
in
![]() $G^*$
is trivial, so
$G^*$
is trivial, so
![]() $\gamma =a^{-1}$
and
$\gamma =a^{-1}$
and
![]() $\phi {\vert }_{A_2}={\mathrm {id}}_{A_2}$
.
$\phi {\vert }_{A_2}={\mathrm {id}}_{A_2}$
.
As
![]() $G^*$
is generated by
$G^*$
is generated by
![]() $A_1\cup A_2$
, we conclude that
$A_1\cup A_2$
, we conclude that
![]() $\phi $
(previously adjusted by a conjugacy to ensure that
$\phi $
(previously adjusted by a conjugacy to ensure that
![]() $\phi _{A_1}={\mathrm {id}}_{A_1}$
) is the identity, and the theorem is proved.
$\phi _{A_1}={\mathrm {id}}_{A_1}$
) is the identity, and the theorem is proved.
Remark 3.2. In the theorem above, we required
![]() $A_1\not \cong A_2$
. An easy way to arrange this is to take
$A_1\not \cong A_2$
. An easy way to arrange this is to take
![]() $A_i=A(d_i)$
from Lemma 2.3 with
$A_i=A(d_i)$
from Lemma 2.3 with
![]() $d_1\neq d_2$
. But one is also free to take both
$d_1\neq d_2$
. But one is also free to take both
![]() $A_i$
to have the same dimension
$A_i$
to have the same dimension
![]() $d\ge 3$
, appealing to [Reference Belilopetsky and Lubotzky1] or Theorem 4.1 below. With this second choice, if G has geometric (or cohomological) dimension D, then
$d\ge 3$
, appealing to [Reference Belilopetsky and Lubotzky1] or Theorem 4.1 below. With this second choice, if G has geometric (or cohomological) dimension D, then
![]() $G^*$
will have geometric (or cohomological) dimension
$G^*$
will have geometric (or cohomological) dimension
![]() $\max \{D, d\}$
.
$\max \{D, d\}$
.
4 Asymmetric hyperbolic 3-manifolds
A closed orientable 3-manifold M is Haken if it is irreducible and contains a closed incompressible surface, that is, a closed surface of positive genus such that the inclusion map
![]() $S\hookrightarrow M$
induces a monomorphism of groups
$S\hookrightarrow M$
induces a monomorphism of groups
![]() $\pi _1S\hookrightarrow \pi _1M$
. If M contains such a surface, then
$\pi _1S\hookrightarrow \pi _1M$
. If M contains such a surface, then
![]() $\pi _1M$
acts without a fixed point on the tree T that is obtained from the universal covering
$\pi _1M$
acts without a fixed point on the tree T that is obtained from the universal covering
![]() $p:\tilde M\to M$
as follows: the vertex set of T is the set of connected components of
$p:\tilde M\to M$
as follows: the vertex set of T is the set of connected components of
![]() $\tilde M \smallsetminus p^{-1}(S)$
; two vertices are connected by an edge if the components that they represent abut along a component of
$\tilde M \smallsetminus p^{-1}(S)$
; two vertices are connected by an edge if the components that they represent abut along a component of
![]() $p^{-1}(S)$
; and the action of
$p^{-1}(S)$
; and the action of
![]() $\pi _1M$
on T is induced by the action of
$\pi _1M$
on T is induced by the action of
![]() $\pi _1M$
on
$\pi _1M$
on
![]() $\tilde M$
by deck transformations.
$\tilde M$
by deck transformations.
In the opposite direction, John Stallings proved that if M is irreducible and
![]() $\pi _1M$
acts without a fixed point on a simplicial tree, then M contains an incompressible surface (see [Reference Stallings19]). In particular, a closed orientable 3-manifold M that is aspherical will be non-Haken if and only if
$\pi _1M$
acts without a fixed point on a simplicial tree, then M contains an incompressible surface (see [Reference Stallings19]). In particular, a closed orientable 3-manifold M that is aspherical will be non-Haken if and only if
![]() $\pi _1M$
has Serre’s property
$\pi _1M$
has Serre’s property
![]() ${\mathrm {FA}}$
.
${\mathrm {FA}}$
.
Our purpose in this section is to explain how well-known facts about hyperbolic 3-manifolds imply the following result, which will be familiar to experts.
Theorem 4.1. There exist infinitely many distinct, closed, asymmetric, hyperbolic
![]() $3$
-manifolds M such that
$3$
-manifolds M such that
![]() $\pi _1M$
has property
$\pi _1M$
has property
![]() ${\mathrm {FA}}$
.
${\mathrm {FA}}$
.
Proof. In the light of the preceding discussion, what we must show is that there are infinitely many distinct hyperbolic 3-manifolds that are asymmetric and non-Haken. The manifolds that we shall describe are obtained by Dehn surgery on the knots shown in Figure 1. These are the only four knots K with at most
![]() $10$
crossings that have the three properties that we are interested in: first, each K is prime and alternating (and nontorus), hence hyperbolic [Reference Menasco13]; second, the knot complement
$10$
crossings that have the three properties that we are interested in: first, each K is prime and alternating (and nontorus), hence hyperbolic [Reference Menasco13]; second, the knot complement
![]() $\mathbb {S}^3\smallsetminus {K}$
has no nontrivial symmetries, so by Mostow rigidity its fundamental group is complete (asymmetric); and third,
$\mathbb {S}^3\smallsetminus {K}$
has no nontrivial symmetries, so by Mostow rigidity its fundamental group is complete (asymmetric); and third,
![]() $\mathbb {S}^3\smallsetminus K$
is small, that is, contains no closed incompressible surface other than the tori parallel to the boundary of a regular neighbourhood of K. The first of these properties is immediately visible in the diagrams, the second is established in the census of Henry and Weeks [Reference Henry and Weeks6] who calculated the symmetry groups of all knots up to 10 crossings (alternatively Kodama and Sakuma [Reference Kodama, Sakuma and Kawauchi9]), and the third is recorded in the census [Reference Burton, Coward, Tillmann, Chan and Klein4] of Burton et al., who calculated all knots with at most 12 crossings that are small.
$\mathbb {S}^3\smallsetminus K$
is small, that is, contains no closed incompressible surface other than the tori parallel to the boundary of a regular neighbourhood of K. The first of these properties is immediately visible in the diagrams, the second is established in the census of Henry and Weeks [Reference Henry and Weeks6] who calculated the symmetry groups of all knots up to 10 crossings (alternatively Kodama and Sakuma [Reference Kodama, Sakuma and Kawauchi9]), and the third is recorded in the census [Reference Burton, Coward, Tillmann, Chan and Klein4] of Burton et al., who calculated all knots with at most 12 crossings that are small.
Thurston’s celebrated Dehn surgery theorem [Reference Thurston20] states that all but finitely many of the closed manifolds obtained by Dehn surgery on these knots will support a hyperbolic metric. And Hatcher’s theorem on boundary slopes [Reference Hatcher5] implies that all but finitely many of these closed manifolds will be non-Haken. Thus, we will be done if we can argue that all but finitely many of these closed hyperbolic manifolds are asymmetric. And this is what Kojima’s arguments show [Reference Kojima10], as we shall now explain.
In Dehn filling, one starts from the manifold
![]() $M_K$
with torus boundary obtained by removing an open tubular neighbourhood of a hyperbolic knot K in
$M_K$
with torus boundary obtained by removing an open tubular neighbourhood of a hyperbolic knot K in
![]() $\mathbb {S}^3$
. A framing of the knot gives an identification
$\mathbb {S}^3$
. A framing of the knot gives an identification
![]() $\mathbb {Z}^2=\pi _1\partial M_k$
. Given a reduced fraction
$\mathbb {Z}^2=\pi _1\partial M_k$
. Given a reduced fraction
![]() $p/q$
, one attaches a thickened 2-disc D to an annular neighbourhood of a simple closed curve on
$p/q$
, one attaches a thickened 2-disc D to an annular neighbourhood of a simple closed curve on
![]() $\partial M_K$
representing the homotopy class
$\partial M_K$
representing the homotopy class
![]() $(p,q)\in \mathbb {Z}^2$
. The boundary of the resulting manifold
$(p,q)\in \mathbb {Z}^2$
. The boundary of the resulting manifold
![]() $M_K\cup D$
is a 2-sphere, which one caps off with a 3-ball to obtain the manifold
$M_K\cup D$
is a 2-sphere, which one caps off with a 3-ball to obtain the manifold
![]() $M_K(p,q)$
. (Note that the union of D and this 3-ball is a solid torus.) For all but finitely many choices of
$M_K(p,q)$
. (Note that the union of D and this 3-ball is a solid torus.) For all but finitely many choices of
![]() $p/q$
, Thurston [Reference Thurston20] provides a hyperbolic metric on
$p/q$
, Thurston [Reference Thurston20] provides a hyperbolic metric on
![]() $M_K(p,q)$
, and by Mostow rigidity this metric is unique. As
$M_K(p,q)$
, and by Mostow rigidity this metric is unique. As
![]() ${\vert }p{\vert }+{\vert }q{\vert }\to \infty $
this metric converges to the complete hyperbolic metric on
${\vert }p{\vert }+{\vert }q{\vert }\to \infty $
this metric converges to the complete hyperbolic metric on
![]() $M_K$
, and when
$M_K$
, and when
![]() ${\vert }p{\vert }+{\vert }q{\vert }$
is sufficiently large, the unique shortest geodesic in
${\vert }p{\vert }+{\vert }q{\vert }$
is sufficiently large, the unique shortest geodesic in
![]() $M_K(p,q)$
is the core of the solid torus added during Dehn filling [Reference Thurston20]. Thus, by restriction, we obtain a homomorphism
$M_K(p,q)$
is the core of the solid torus added during Dehn filling [Reference Thurston20]. Thus, by restriction, we obtain a homomorphism
![]() ${\mathrm {Isom}}(M_K(p,q))\to {\mathrm {Homeo}}(M_K^{\prime })$
, where
${\mathrm {Isom}}(M_K(p,q))\to {\mathrm {Homeo}}(M_K^{\prime })$
, where
![]() $M_K^{\prime }$
is the interior of
$M_K^{\prime }$
is the interior of
![]() $M_K$
. By Mostow rigidity, every homeomorphism of
$M_K$
. By Mostow rigidity, every homeomorphism of
![]() $M_K^{\prime }$
is homotopic to a unique isometry of the complete hyperbolic metric on
$M_K^{\prime }$
is homotopic to a unique isometry of the complete hyperbolic metric on
![]() $M_K^{\prime }$
, so, passing to homotopy classes, we have a homomorphism
$M_K^{\prime }$
, so, passing to homotopy classes, we have a homomorphism
![]() $\rho :{\mathrm {Isom}}(M_K(p,q))\to {\mathrm {Isom}}(M_K^{\prime })$
(where the isometries of
$\rho :{\mathrm {Isom}}(M_K(p,q))\to {\mathrm {Isom}}(M_K^{\prime })$
(where the isometries of
![]() $M_K^{\prime }$
are with respect to its complete hyperbolic metric, not the restriction of the metric on
$M_K^{\prime }$
are with respect to its complete hyperbolic metric, not the restriction of the metric on
![]() $M_K(p,q)$
). Mostow rigidity also tells us that, for any complete, finite-volume hyperbolic
$M_K(p,q)$
). Mostow rigidity also tells us that, for any complete, finite-volume hyperbolic
![]() $3$
-manifold N, the natural map
$3$
-manifold N, the natural map
![]() ${\mathrm {Isom}}(N)\to {\mathrm {Out}}(\pi _1N)$
is an isomorphism. Thus, an isometry
${\mathrm {Isom}}(N)\to {\mathrm {Out}}(\pi _1N)$
is an isomorphism. Thus, an isometry
![]() $\phi $
of
$\phi $
of
![]() $M_K(p,q)$
will lie in the kernel of
$M_K(p,q)$
will lie in the kernel of
![]() $\rho $
only if its restriction to
$\rho $
only if its restriction to
![]() $M_K^{\prime }$
induces an inner automorphism of
$M_K^{\prime }$
induces an inner automorphism of
![]() $\pi _1 M_K$
. But if this is the case, then the map that
$\pi _1 M_K$
. But if this is the case, then the map that
![]() $\phi $
induces on
$\phi $
induces on
![]() $\pi _1M_K(p,q)$
(a quotient of
$\pi _1M_K(p,q)$
(a quotient of
![]() $\pi _1 M_K^{\prime }$
) will also be inner, and therefore
$\pi _1 M_K^{\prime }$
) will also be inner, and therefore
![]() $\phi $
is trivial. Thus,
$\phi $
is trivial. Thus,
![]() ${\rho :{\mathrm {Isom}}(M_K(p,q))\to {\mathrm {Isom}}(M_K^{\prime })}$
is injective. In particular, for K with
${\rho :{\mathrm {Isom}}(M_K(p,q))\to {\mathrm {Isom}}(M_K^{\prime })}$
is injective. In particular, for K with
![]() $\pi _1M_K$
complete, the triviality of
$\pi _1M_K$
complete, the triviality of
![]() ${\mathrm {Isom}}(M_K^{\prime })\cong {\mathrm {Out}}(\pi _1M')$
implies that
${\mathrm {Isom}}(M_K^{\prime })\cong {\mathrm {Out}}(\pi _1M')$
implies that
![]() $ {\mathrm {Out}}(\pi _1M_K(p,q))\cong { \mathrm {Isom}}(M_K(p,q))$
is trivial when
$ {\mathrm {Out}}(\pi _1M_K(p,q))\cong { \mathrm {Isom}}(M_K(p,q))$
is trivial when
![]() ${\vert }p{\vert }+{\vert }q{\vert }$
is sufficiently large.
${\vert }p{\vert }+{\vert }q{\vert }$
is sufficiently large.
We shall also need the following lemma. Note that a finitely generated group with property FA has finite abelianisation.
Lemma 4.2. Let M be a closed hyperbolic
![]() $3$
-manifold. If
$3$
-manifold. If
![]() $H_1M$
is finite, then every nontrivial homomorphism
$H_1M$
is finite, then every nontrivial homomorphism
![]() $f: \pi _1M\to \pi _1M$
is an isomorphism.
$f: \pi _1M\to \pi _1M$
is an isomorphism.
Proof. Scott’s compact core theorem [Reference Scott16] implies that every nontrivial subgroup of infinite index in
![]() $\pi _1M$
has infinite abelianisation, and therefore cannot be the image of f. In more detail, if the finitely generated group
$\pi _1M$
has infinite abelianisation, and therefore cannot be the image of f. In more detail, if the finitely generated group
![]() $G=f(\pi _1M)$
has infinite index, then the corresponding covering space
$G=f(\pi _1M)$
has infinite index, then the corresponding covering space
![]() $M'=\tilde M/G$
of M has a compact submanifold C such that
$M'=\tilde M/G$
of M has a compact submanifold C such that
![]() $C\hookrightarrow M'$
is a homotopy equivalence. A standard argument using Poincaré–Lefschetz duality (‘half lives, half dies’) shows that the rank of
$C\hookrightarrow M'$
is a homotopy equivalence. A standard argument using Poincaré–Lefschetz duality (‘half lives, half dies’) shows that the rank of
![]() $H_1(\partial C)$
is twice the rank of the image of
$H_1(\partial C)$
is twice the rank of the image of
![]() $H_1(\partial C)$
in
$H_1(\partial C)$
in
![]() $H_1M'$
. Since C has at least one component of positive genus, both
$H_1M'$
. Since C has at least one component of positive genus, both
![]() $H_1\partial C$
and
$H_1\partial C$
and
![]() $H_1M'$
are infinite.
$H_1M'$
are infinite.
The lemma now follows from the fact that every epimorphism from
![]() $\pi _1M$
to a subgroup of finite index in itself is an isomorphism (see [Reference Bridson, Hinkkanen and Martin2] or [Reference Sela17]). In more detail, an argument of Hirshon [Reference Hirshon7] shows that if a finitely generated, torsion-free group
$\pi _1M$
to a subgroup of finite index in itself is an isomorphism (see [Reference Bridson, Hinkkanen and Martin2] or [Reference Sela17]). In more detail, an argument of Hirshon [Reference Hirshon7] shows that if a finitely generated, torsion-free group
![]() $\Gamma $
is residually finite, then every homomorphism from
$\Gamma $
is residually finite, then every homomorphism from
![]() $\Gamma $
to a subgroup of finite index in itself is injective, and Mostow rigidity implies that
$\Gamma $
to a subgroup of finite index in itself is injective, and Mostow rigidity implies that
![]() $\pi _1M$
(which is residually finite because it is linear, and torsion-free because M is aspherical) cannot be isomorphic to a subgroup of finite index in itself (because such a subgroup has greater covolume).
$\pi _1M$
(which is residually finite because it is linear, and torsion-free because M is aspherical) cannot be isomorphic to a subgroup of finite index in itself (because such a subgroup has greater covolume).
5 The proof of Theorem A
Towards proving items (2) and (3) of the theorem, first note that the process by which a given finitely generated group G was transformed into the conditioned state described in Corollary 2.2 involved only free products with free groups, so it preserves the finiteness properties in (3), and any finite subgroup of the conditioned group is conjugate to a subgroup of the original G. This last property is also true in the case of a countable group that is first embedded in a finitely generated group using Neumann’s embedding (as we noted in Section 2).
In the main construction, we defined
![]() $G^* = A_1\ast _{F_1} G\ast _{F_2} A_2$
, where the
$G^* = A_1\ast _{F_1} G\ast _{F_2} A_2$
, where the
![]() $A_i$
are torsion-free and the
$A_i$
are torsion-free and the
![]() $F_i$
are finitely generated free groups. Every finite subgroup of an amalgamated free product is conjugate to one of the vertex groups, and amalgamating groups that are finitely presented (respectively, have a finite classifying space of dimension at most d) along finitely generated free groups preserves these properties. Thus, (2) is proved, and (3) will be proved if we can argue that both
$F_i$
are finitely generated free groups. Every finite subgroup of an amalgamated free product is conjugate to one of the vertex groups, and amalgamating groups that are finitely presented (respectively, have a finite classifying space of dimension at most d) along finitely generated free groups preserves these properties. Thus, (2) is proved, and (3) will be proved if we can argue that both
![]() $A_1$
and
$A_1$
and
![]() $A_2$
can be taken to be three-dimensional hyperbolic groups.
$A_2$
can be taken to be three-dimensional hyperbolic groups.
In the light of Theorems 3.1 and 4.1, the following proposition completes the proof of Theorem A.
Proposition 5.1. If the complete groups
![]() $A_1\not \cong A_2$
used in the construction of
$A_1\not \cong A_2$
used in the construction of
![]() $G^*$
are the fundamental groups of hyperbolic
$G^*$
are the fundamental groups of hyperbolic
![]() $3$
-manifolds that have property
$3$
-manifolds that have property
![]() ${\mathrm {FA}}$
, then
${\mathrm {FA}}$
, then
![]() $G^*$
is hopfian.
$G^*$
is hopfian.
Proof. We have
![]() $G^* = A_1\ast _{F_1} G \ast _{F_2} A_2$
. Let
$G^* = A_1\ast _{F_1} G \ast _{F_2} A_2$
. Let
![]() $\phi :G^*\to G^*$
be an epimorphism. The action of
$\phi :G^*\to G^*$
be an epimorphism. The action of
![]() $\phi (A_1)$
on the Bass–Serre tree for
$\phi (A_1)$
on the Bass–Serre tree for
![]() $G^*$
has a fixed point, as
$G^*$
has a fixed point, as
![]() $A_1$
has property FA, so
$A_1$
has property FA, so
![]() $\phi (A_1)$
lies in a conjugate of one of the vertex groups,
$\phi (A_1)$
lies in a conjugate of one of the vertex groups,
![]() $A_1, G, A_2$
. The same argument applies to
$A_1, G, A_2$
. The same argument applies to
![]() $A_2$
.
$A_2$
.
As in the proof of Theorem 3.1, we use the fact that a pair of conjugates of
![]() $A_1, A_2$
or G can only generate
$A_1, A_2$
or G can only generate
![]() $G^*$
if one of the pair is a conjugate of
$G^*$
if one of the pair is a conjugate of
![]() $A_1$
and the other is a conjugate of
$A_1$
and the other is a conjugate of
![]() $A_2$
. From this, and the surjectivity of
$A_2$
. From this, and the surjectivity of
![]() $\phi $
, we deduce that
$\phi $
, we deduce that
![]() $\phi ^2(A_1)$
is a nontrivial subgroup of a conjugate of
$\phi ^2(A_1)$
is a nontrivial subgroup of a conjugate of
![]() $A_1$
and
$A_1$
and
![]() $\phi ^2(A_2)$
is a nontrivial subgroup of a conjugate of
$\phi ^2(A_2)$
is a nontrivial subgroup of a conjugate of
![]() $A_2$
. Lemma 4.2 then forces
$A_2$
. Lemma 4.2 then forces
![]() $\phi ^2{\vert }_{A_1}$
and
$\phi ^2{\vert }_{A_1}$
and
![]() $\phi ^2{\vert }_{A_2}$
to be isomorphisms onto conjugates of
$\phi ^2{\vert }_{A_2}$
to be isomorphisms onto conjugates of
![]() $A_1$
and
$A_1$
and
![]() $A_2$
, respectively. We can then proceed exactly as in the proof of Theorem 3.1 to conclude that
$A_2$
, respectively. We can then proceed exactly as in the proof of Theorem 3.1 to conclude that
![]() $\phi $
is an inner automorphism of
$\phi $
is an inner automorphism of
![]() $G^*$
.
$G^*$
.
Remark 5.2. (1). Let G be a group that has a finite classifying space and contains an element
![]() $\gamma \neq 1$
conjugate to its inverse. Our construction embeds G in a group
$\gamma \neq 1$
conjugate to its inverse. Our construction embeds G in a group
![]() $G^*$
that retains these properties and is complete. This recovers the main theorem of [Reference Bridson and Short3]. To obtain a specific example, one can take
$G^*$
that retains these properties and is complete. This recovers the main theorem of [Reference Bridson and Short3]. To obtain a specific example, one can take
![]() $G=\langle {x,y\mid xyx^{-1}y}\rangle $
.
$G=\langle {x,y\mid xyx^{-1}y}\rangle $
.
(2) A second (less concise and explicit) proof of Theorem A can be obtained by means of a careful application of relative small cancellation theory, following Miller and Schupp’s method in [Reference Miller and Schupp14] but avoiding the use of finite groups. In outline, one constructs a two-generator perfect hyperbolic group B, takes a free product
![]() $(G\times \mathbb {Z}^2)* (B\times \mathbb {Z})$
and then forms the quotient by a set of relators satisfying a strong small cancellation condition [Reference Osin15]. A key point in [Reference Miller and Schupp14] is that automorphisms preserve the different finite orders of elements, while here they preserve the different ranks of centralisers of elements.
$(G\times \mathbb {Z}^2)* (B\times \mathbb {Z})$
and then forms the quotient by a set of relators satisfying a strong small cancellation condition [Reference Osin15]. A key point in [Reference Miller and Schupp14] is that automorphisms preserve the different finite orders of elements, while here they preserve the different ranks of centralisers of elements.