Article contents
The bandwidth theorem for locally dense graphs
Published online by Cambridge University Press: 04 November 2020
Abstract
The bandwidth theorem of Böttcher, Schacht, and Taraz [Proof of the bandwidth conjecture of Bollobás and Komlós, Mathematische Annalen, 2009] gives a condition on the minimum degree of an n-vertex graph G that ensures G contains every r-chromatic graph H on n vertices of bounded degree and of bandwidth 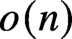 $o(n)$, thereby proving a conjecture of Bollobás and Komlós [The Blow-up Lemma, Combinatorics, Probability, and Computing, 1999]. In this paper, we prove a version of the bandwidth theorem for locally dense graphs. Indeed, we prove that every locally dense n-vertex graph G with
$o(n)$, thereby proving a conjecture of Bollobás and Komlós [The Blow-up Lemma, Combinatorics, Probability, and Computing, 1999]. In this paper, we prove a version of the bandwidth theorem for locally dense graphs. Indeed, we prove that every locally dense n-vertex graph G with 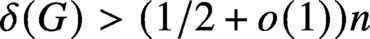 $\delta (G)> (1/2+o(1))n$ contains as a subgraph any given (spanning) H with bounded maximum degree and sublinear bandwidth.
$\delta (G)> (1/2+o(1))n$ contains as a subgraph any given (spanning) H with bounded maximum degree and sublinear bandwidth.
Keywords
MSC classification
Information
- Type
- Discrete Mathematics
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 7
- Cited by


