Hostname: page-component-5b777bbd6c-gcwzt Total loading time: 0 Render date: 2025-06-18T17:17:25.666Z Has data issue: false hasContentIssue false
  • English
  • Français

Tree universality in positional games

Part of: Game theory Graph theory

Published online by Cambridge University Press:  13 December 2024

Grzegorz Adamski Open the ORCID record for Grzegorz Adamski [Opens in a new window] ,
Sylwia Antoniuk Open the ORCID record for Sylwia Antoniuk [Opens in a new window] ,
Małgorzata Bednarska-Bzdȩga Open the ORCID record for Małgorzata Bednarska-Bzdȩga [Opens in a new window] ,
Dennis Clemens Open the ORCID record for Dennis Clemens [Opens in a new window] ,
Fabian Hamann Open the ORCID record for Fabian Hamann [Opens in a new window]  and
Yannick Mogge Open the ORCID record for Yannick Mogge [Opens in a new window]
Grzegorz Adamski
Affiliation:
Department of Discrete Mathematics, Faculty of Mathematics and CS, Adam Mickiewicz University, Poznań, Poland
Sylwia Antoniuk
Affiliation:
Department of Discrete Mathematics, Faculty of Mathematics and CS, Adam Mickiewicz University, Poznań, Poland
Małgorzata Bednarska-Bzdȩga
Affiliation:
Department of Discrete Mathematics, Faculty of Mathematics and CS, Adam Mickiewicz University, Poznań, Poland
Dennis Clemens
Affiliation:
Institute of Mathematics, Hamburg University of Technology, Hamburg, Germany
Fabian Hamann
Affiliation:
Institute of Mathematics, Hamburg University of Technology, Hamburg, Germany
Yannick Mogge*
Affiliation:
Institute of Mathematics, Hamburg University of Technology, Hamburg, Germany
*
Corresponding author: Yannick Mogge; Email: yannick.mogge@tuhh.de
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we consider positional games where the winning sets are edge sets of tree-universal graphs. Specifically, we show that in the unbiased Maker-Breaker game on the edges of the complete graph 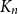$K_n$, Maker has a strategy to claim a graph which contains copies of all spanning trees with maximum degree at most 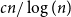$cn/\log (n)$, for a suitable constant $c$ and $n$ being large enough. We also prove an analogous result for Waiter-Client games. Both of our results show that the building player can play at least as good as suggested by the random graph intuition. Moreover, they improve on a special case of earlier results by Johannsen, Krivelevich, and Samotij as well as Han and Yang for Maker-Breaker games.

Keywords

Maker-Breaker gamesWaiter-Client gamestreeembeddinguniversalityexpander

MSC classification

Primary: 91A24: Positional games (pursuit and evasion, etc.)
Secondary: 05C05: Trees
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 34 , Issue 3 , May 2025 , pp. 338 - 358
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

*

The research of the fourth and sixth author is supported by Deutsche Forschungsgemeinschaft (Project CL 903/1-1)

References

Adamski, G., Antoniuk, S., Bednarska-Bzdȩga, M., Clemens, D., Hamann, F. and Mogge, Y. (2024) Creating spanning trees in Waiter-Client games, arXiv preprint arXiv: 2403.18534.Google Scholar
Balogh, J., Martin, R. and Pluhár, A. (2009) The diameter game. Random Struct. Algor. 35(3) 369–389.CrossRefGoogle Scholar
Barkey, J., Clemens, D., Hamann, F., Mikalački, M. and Sgueglia, A. (2023) Multistage positional games. Discrete Math. 346(9) 113478.CrossRefGoogle Scholar
Beck, J. (2008) Combinatorial Games: Tic-Tac-Toe Theory. vol. 114. Cambridge University Press.CrossRefGoogle Scholar
Bednarska-Bzdȩga, M. (2013) On weight function methods in Chooser–Picker games. Theor. Comput. Sci. 475 21–33 Google Scholar
Bednarska-Bzdȩga, M., Hefetz, D., Krivelevich, M. and Łuczak, T. (2016) Manipulative waiters with probabilistic intuition. Comb. Prob. Comp. 25(6) 823–849.CrossRefGoogle Scholar
Chvátal, V. and Erdös, P. (1978) Biased positional games. Ann. Discrete Math. 2 221–229.CrossRefGoogle Scholar
Clemens, D., Ferber, A., Glebov, R., Hefetz, D. and Liebenau, A. (2015) Building spanning trees quickly in Maker-Breaker games. SIAM J. Discrete Math. 29(3) 1683–1705.CrossRefGoogle Scholar
Clemens, D., Ferber, A., Krivelevich, M. and Liebenau, A. (2012) Fast strategies in Maker–Breaker games played on random boards. Comb. Prob. Comp. 21(6) 897–915.CrossRefGoogle Scholar
Clemens, D., Gupta, P., Hamann, F., Haupt, A., Mikalački, M. and Mogge, Y. (2020) Fast strategies in Waiter-Client games. Electron. J. Comb. 27(3) 1–35.Google Scholar
András Csernenszky, C. I. M. and Pluhár, A. (2009) On Chooser-Picker positional games. Discrete Math. 309(16) 5141–5146.CrossRefGoogle Scholar
Dean, O. and Krivelevich, M. (2016) Client-Waiter games on complete and random graphs. Electron. J. Comb. 23(4) 1–31.Google Scholar
Dvořák, V. (2023) Waiter-Client clique-factor game. Discrete Math. 346(1) 113191.CrossRefGoogle Scholar
Erdős, P. and Selfridge, J. L. (1973) On a combinatorial game. J. Comb. Theory, A 14(3) 298–301.CrossRefGoogle Scholar
Ferber, A., Hefetz, D. and Krivelevich, M. (2012) Fast embedding of spanning trees in biased Maker-Breaker games. Eur. J. Combin. 33(6) 1086–1099.CrossRefGoogle Scholar
Gebauer, H. and Szabó, T. (2009) Asymptotic random graph intuition for the biased connectivity game. Random Struct. Algor. 35(4) 431–443.CrossRefGoogle Scholar
Han, J. and Yang, D. (2022) Spanning trees in sparse expanders, arXiv preprint arXiv: 2211.04758.Google Scholar
Haxell, P. E. (2001) Tree embeddings. J. Graph Theor. 36(3) 121–130.3.0.CO;2-U>CrossRefGoogle Scholar
Hefetz, D., Krivelevich, M., Stojaković, M. and Szabó, T. (2009) Fast winning strategies in Maker-Breaker games. J. Comb. Theory, Ser. B 99(1) 39–47.CrossRefGoogle Scholar
Hefetz, D., Krivelevich, M., Stojaković, M. and Szabó, T. (2009) A sharp threshold for the Hamilton cycle Maker-Breaker game. Random Struct. Algor. 34(1) 112–122.CrossRefGoogle Scholar
Hefetz, D., Krivelevich, M., Stojaković, M. and Szabó, T. (2014) Positional Games, vol. 44, Springer.CrossRefGoogle Scholar
Hefetz, D., Krivelevich, M. and Tan, W. E. (2016) Waiter-Client and Client-Waiter planarity, colorability and minor games. Discrete Math. 339(5) 1525–1536.CrossRefGoogle Scholar
Janson, S. Łuczak, T. and Ruciński, A. (2011) Random Graphs. John Wiley & Sons.Google Scholar
Johannsen, D., Krivelevich, M. and Samotij, W. (2013) Expanders are universal for the class of all spanning trees. Comb. Prob. Comp. 22(2) 253–281.CrossRefGoogle Scholar
Krivelevich, M. (2010) Embedding spanning trees in random graphs. SIAM J. Discrete Math. 24(4) 1495–1500.CrossRefGoogle Scholar
Lehman, A. (1964) A solution of the Shannon switching game. J. Soc. Ind. Appl. Math. 12(4) 687–725.CrossRefGoogle Scholar
Liebenau, A. and Nenadov, R. (2022) The threshold bias of the clique-factor game. J. Comb. Theory Ser. B 152 221–247.CrossRefGoogle Scholar
Lu, X. (1991) A matching game. Discrete Math. 94(3) 199–207.CrossRefGoogle Scholar
West, D. B. (2001) Introduction to Graph Theory, vol. 2. Prentice Hall.Google Scholar