We provide two constructions of Gaussian random holomorphic sections of a Hermitian holomorphic line bundle $(L,h_{L})$ on a Hermitian complex manifold $(X,\Theta )$, that are particularly interesting in the case where the space of $\mathcal {L}^2$-holomorphic sections $H^{0}_{(2)}(X,L)$ is infinite dimensional. We first provide a general construction of Gaussian random holomorphic sections of L, which, if $H^{0}_{(2)}(X,L)$ is infinite dimensional, are almost never $\mathcal {L}^2$-integrable on X. The second construction combines the abstract Wiener space theory with the Berezin–Toeplitz quantization and yields a Gaussian ensemble of random $\mathcal {L}^2$-holomorphic sections. Furthermore, we study their random zeros in the context of semiclassical limits, including their distributions, large deviation estimates, local fluctuations and hole probabilities.

We give sufficient conditions for the essential spectrum of the Hermitian square of a class of Hankel operators on the Bergman space of the polydisc to contain intervals. We also compute the spectrum in case the symbol is a monomial.

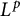We study the $L^p$ regularity of the Bergman projection P over the symmetrized polydisc in $\mathbb C^n$. We give a decomposition of the Bergman projection on the polydisc and obtain an operator equivalent to the Bergman projection over antisymmetric function spaces. Using it, we obtain the $L^p$ irregularity of P for $p=\frac {2n}{n-1}$ which also implies that P is $L^p$ bounded if and only if $p\in (\frac {2n}{n+1},\frac {2n}{n-1})$.

In this paper, we construct a natural probability measure on the space of real branched coverings from a real projective algebraic curve $(X,c_X)$ to the projective line $(\mathbb{C} \mathbb {P}^1,\textit{conj} )$. We prove that the space of degree d real branched coverings having “many” real branched points (for example, more than $\sqrt {d}^{1+\alpha }$, for any $\alpha>0$) has exponentially small measure. In particular, maximal real branched coverings – that is, real branched coverings such that all the branched points are real – are exponentially rare.

We present some fundamental properties of quasi-Reinhardt domains, in connection with Kobayashi hyperbolicity, minimal domains and representative domains. We also study proper holomorphic correspondences between quasi-Reinhardt domains.

We show that the modulus of the Bergman kernel $\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}B(z, \zeta )$ of a general homogeneous Siegel domain of type II is ‘almost constant’ uniformly with respect to $z$ when $\zeta $ varies inside a Bergman ball. The control is expressed in terms of the Bergman distance. This result was proved by A. Korányi for symmetric Siegel domains of type II. Subsequently, R. R. Coifman and R. Rochberg used it to establish an atomic decomposition theorem and an interpolation theorem by functions in Bergman spaces $A^p$ on these domains. The atomic decomposition theorem and the interpolation theorem are extended here to the general homogeneous case using the same tools. We further extend the range of exponents $p$ via functional analysis using recent estimates.

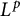
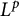
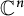
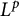
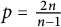
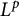
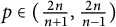
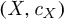
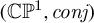
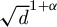
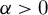
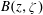
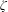
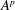
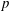
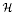It is well known in Kähler geometry that the infinite-dimensional symmetric space of smooth Kähler metrics in a fixed Kähler class on a polarized Kähler manifold is well approximated by finite-dimensional submanifolds 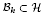of Bergman metrics of height 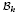k. Then it is natural to ask whether geodesics in can be approximated by Bergman geodesics in . 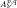For any polarized Kähler manifold, the approximation is in the C0 topology. For some special varieties, one expects better convergence: Song and Zelditch proved the C2 convergence for the torus-invariant metrics over toric varieties. In this article, we show that some C∞ approximation exists as well as a complete asymptotic expansion for principally polarized abelian varieties.

We study the boundedness properties of Rudin–Forelli-type operators associated to tubular domains over symmetric cones. As an application, we give a characterization of the topological dual space of the weighted Bergman space .

In this paper we consider the dynamical system involved by the Ricci operator on the space of Kähler metrics of a Fano manifold. Nadel has defined an iteration scheme given by the Ricci operator and asked whether it has some non-trivial periodic points. First, we prove that no such periodic points can exist. We define the inverse of the Ricci operator and consider the dynamical behaviour of its iterates for a Fano Kähler–Einstein manifold. Then we define a finite-dimensional procedure to give an approximation of Kähler–Einstein metrics using this iterative procedure and apply it on ℂℙ2 blown up in three points.

We prove that the Bergman projection on $L^p(w)$ $(p\neq 2)$, where $w(r)=(1-r^2)^A\textrm{e}^{-B/(1-r^2)^{\alpha}}$, is not bounded.

AMS 2000 Mathematics subject classification: Primary 47B10