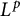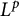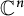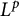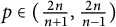1 Introduction
Let
![]() $\Omega $
be a domain in the complex Euclidean space
$\Omega $
be a domain in the complex Euclidean space
![]() $\mathbb C^n$
. Let
$\mathbb C^n$
. Let
![]() $dV$
denote the Lebesgue measure. The Bergman projection
$dV$
denote the Lebesgue measure. The Bergman projection
![]() $P_\Omega $
is the orthogonal projection from
$P_\Omega $
is the orthogonal projection from
![]() $L^2(\Omega )$
onto the Bergman space
$L^2(\Omega )$
onto the Bergman space
![]() $A^2(\Omega )$
, the space of all square-integrable holomorphic functions. Associated with
$A^2(\Omega )$
, the space of all square-integrable holomorphic functions. Associated with
![]() $P_\Omega $
, there is a unique function
$P_\Omega $
, there is a unique function
![]() $K_\Omega $
on
$K_\Omega $
on
![]() $\Omega \times \Omega $
such that for any
$\Omega \times \Omega $
such that for any
![]() $f\in L^2(\Omega )$
:
$f\in L^2(\Omega )$
:
The positive Bergman operator
![]() $P^+_{\Omega }$
is given by
$P^+_{\Omega }$
is given by
By its definition, the Bergman projection is
![]() $L^2$
bounded. An active area of research in several complex variables and harmonic analysis considers the
$L^2$
bounded. An active area of research in several complex variables and harmonic analysis considers the
![]() $L^p$
regularity of
$L^p$
regularity of
![]() $P_\Omega $
for
$P_\Omega $
for
![]() $p\neq 2$
. In particular, people are interested in the connection between the boundary geometry of pseudoconvex domains and the
$p\neq 2$
. In particular, people are interested in the connection between the boundary geometry of pseudoconvex domains and the
![]() $L^p$
behavior of the projection. On a wide class of domains, the Bergman projection is
$L^p$
behavior of the projection. On a wide class of domains, the Bergman projection is
![]() $L^p$
regular for all
$L^p$
regular for all
![]() $1<p<\infty $
(see, for instance, [Reference Barrett and ŞahutoğluBŞ12, Reference Charpentier and DupainCD06, Reference Ehsani and LiebEL08, Reference FeffermanFef74, Reference McNealMcN89, Reference McNealMcN94a, Reference McNealMcN94b, Reference McNeal and SteinMS94, Reference Nagel, Rosay, Stein and WaingerNRSW88, Reference Phong and SteinPS77]). On some other domains, the projection has only a finite range of mapping regularity (see, for example, [Reference Bender, Chakrabarti, Edholm and MainkarBCEM22, Reference ChenChe17, Reference Chen, Jin and YuanCJY20, Reference Chen, Krantz and YuanCKY20, Reference Chakrabarti and ZeytuncuCZ16, Reference Edholm and McNealEM16, Reference Edholm and McNealEM17, Reference ZeytuncuZey13]). We also refer to [Reference ZeytuncuZey20] for a survey on the problem.
$1<p<\infty $
(see, for instance, [Reference Barrett and ŞahutoğluBŞ12, Reference Charpentier and DupainCD06, Reference Ehsani and LiebEL08, Reference FeffermanFef74, Reference McNealMcN89, Reference McNealMcN94a, Reference McNealMcN94b, Reference McNeal and SteinMS94, Reference Nagel, Rosay, Stein and WaingerNRSW88, Reference Phong and SteinPS77]). On some other domains, the projection has only a finite range of mapping regularity (see, for example, [Reference Bender, Chakrabarti, Edholm and MainkarBCEM22, Reference ChenChe17, Reference Chen, Jin and YuanCJY20, Reference Chen, Krantz and YuanCKY20, Reference Chakrabarti and ZeytuncuCZ16, Reference Edholm and McNealEM16, Reference Edholm and McNealEM17, Reference ZeytuncuZey13]). We also refer to [Reference ZeytuncuZey20] for a survey on the problem.
In this article, we focus on the Bergman projection on the symmetrized polydisc
![]() $\mathbb G^n$
. Let
$\mathbb G^n$
. Let
![]() $\mathbb D^n$
denote the polydisc in
$\mathbb D^n$
denote the polydisc in
![]() $\mathbb C^n$
. Let
$\mathbb C^n$
. Let
![]() $\Phi _n$
be the rational holomorphic mapping on
$\Phi _n$
be the rational holomorphic mapping on
![]() $\mathbb C^n$
given by
$\mathbb C^n$
given by
![]() $\Phi _n(w_1,\dots ,w_n)=(p_1(w),\dots , p_n(w)),$
where
$\Phi _n(w_1,\dots ,w_n)=(p_1(w),\dots , p_n(w)),$
where
![]() $p_j(w)$
is the symmetric polynomial in w of degree j:
$p_j(w)$
is the symmetric polynomial in w of degree j:
The symmetrized polydisc
![]() $\mathbb G^n$
is the image of
$\mathbb G^n$
is the image of
![]() $\mathbb D^n$
under
$\mathbb D^n$
under
![]() $\Phi _n$
:
$\Phi _n$
:
When
![]() $n=2$
, the symmetrized bidisc
$n=2$
, the symmetrized bidisc
serves as an interesting example in several complex variables. It is a first known example of many phenomena. We list some of them here below:
-
• The Lempert theorem may hold on bounded pseudoconvex domains that are not biholomorphically equivalent to any convex domains [Reference Agler and YoungAY04].
-
• Bounded
 $\mathbb C$
-convex domains are not necessarily biholomorphically equivalent to convex ones [Reference Nikolov, Pflug and ZwonekNPZ08].
$\mathbb C$
-convex domains are not necessarily biholomorphically equivalent to convex ones [Reference Nikolov, Pflug and ZwonekNPZ08].
See also [Reference Agler, Lykova and YoungALY18, Reference Agler and YoungAY00, Reference SarkarSar15] for some recent work on
![]() $\mathbb G$
.
$\mathbb G$
.
In addition, the symmetrized polydisc
![]() $\mathbb G^n$
also serves as an example of a quotient domain and is biholomorphically equivalent to
$\mathbb G^n$
also serves as an example of a quotient domain and is biholomorphically equivalent to
![]() $\mathbb D^n/\mathcal S_n,$
where
$\mathbb D^n/\mathcal S_n,$
where
![]() $\mathcal S_n$
is the group of permutations of n coordinate variables in
$\mathcal S_n$
is the group of permutations of n coordinate variables in
![]() $\mathbb C^n$
. See [Reference Dall’Ara and MonguzziDM23, Reference GhoshGho21] for some recent studies regarding Bergman projections over quotient domains of the form
$\mathbb C^n$
. See [Reference Dall’Ara and MonguzziDM23, Reference GhoshGho21] for some recent studies regarding Bergman projections over quotient domains of the form
![]() $\Omega /G$
.
$\Omega /G$
.
Partially due to
![]() $\mathbb G^2$
’s interesting properties, the
$\mathbb G^2$
’s interesting properties, the
![]() $L^p$
regularity of
$L^p$
regularity of
![]() $P_{\mathbb G^2}$
and
$P_{\mathbb G^2}$
and
![]() $P_{\mathbb G^n}$
has also attracted attention in recent years. In [Reference Chen, Krantz and YuanCKY20], Chen, Krantz, and Yuan showed that
$P_{\mathbb G^n}$
has also attracted attention in recent years. In [Reference Chen, Krantz and YuanCKY20], Chen, Krantz, and Yuan showed that
![]() $P_{\mathbb G^n}$
is
$P_{\mathbb G^n}$
is
![]() $L^p$
bounded for
$L^p$
bounded for
![]() $p\in (1+\frac {n-1}{\sqrt {n^2-1}},1+\frac {\sqrt {n^2-1}}{n-1})$
. Later, Chen, Jin, and Yuan [Reference Chen, Jin and YuanCJY20] improved the
$p\in (1+\frac {n-1}{\sqrt {n^2-1}},1+\frac {\sqrt {n^2-1}}{n-1})$
. Later, Chen, Jin, and Yuan [Reference Chen, Jin and YuanCJY20] improved the
![]() $L^p$
regular range of
$L^p$
regular range of
![]() $P_{\mathbb G}$
to
$P_{\mathbb G}$
to
![]() $({4}/{3},4)$
and established the Sobolev estimates for
$({4}/{3},4)$
and established the Sobolev estimates for
![]() $P_{\mathbb G}$
. While preparing this article, the authors were informed of a discrepancy between the arXiv version of [Reference Chen, Jin and YuanCJY20] and the version those authors submitted to a journal for publication. In a recent update of [Reference Chen, Jin and YuanCJY20] posted to the arXiv, the range of
$P_{\mathbb G}$
. While preparing this article, the authors were informed of a discrepancy between the arXiv version of [Reference Chen, Jin and YuanCJY20] and the version those authors submitted to a journal for publication. In a recent update of [Reference Chen, Jin and YuanCJY20] posted to the arXiv, the range of
![]() $L^p$
regularity for the symmetrized polydisc is at least
$L^p$
regularity for the symmetrized polydisc is at least
![]() $(\frac {2n}{n+1},\frac {2n}{n-1})$
, see [Reference Chen, Jin and YuanCJY23, Remark 1.5]. The main idea in the proof of these results is to use Bell’s transformation formula [Reference BellBel81] to reformulate the
$(\frac {2n}{n+1},\frac {2n}{n-1})$
, see [Reference Chen, Jin and YuanCJY23, Remark 1.5]. The main idea in the proof of these results is to use Bell’s transformation formula [Reference BellBel81] to reformulate the
![]() $L^p$
regularity problem of
$L^p$
regularity problem of
![]() $P_{\mathbb G^n}$
into a weighted
$P_{\mathbb G^n}$
into a weighted
![]() $L^p$
regularity problem of
$L^p$
regularity problem of
![]() $P_{\mathbb D^n}$
over a weighted
$P_{\mathbb D^n}$
over a weighted
![]() $L^p$
space of antisymmetric functions. Yet, the precise
$L^p$
space of antisymmetric functions. Yet, the precise
![]() $L^p$
regular range for
$L^p$
regular range for
![]() $P_{\mathbb G^n}$
was not previously known.
$P_{\mathbb G^n}$
was not previously known.
There are mainly two challenges on obtaining the sharp
![]() $L^p$
estimates of
$L^p$
estimates of
![]() $P_{\mathbb G^n}$
: 1. the complexity of the Jacobian of
$P_{\mathbb G^n}$
: 1. the complexity of the Jacobian of
![]() $(p_1,\dots ,p_n)$
for large n dimension makes estimations complicated. 2. The cancellation caused by integrating antisymmetric functions creates obstacles to precisely analyze the (un)boundedness of the operator. To us, the second issue is more crucial and distinguishes the problem on
$(p_1,\dots ,p_n)$
for large n dimension makes estimations complicated. 2. The cancellation caused by integrating antisymmetric functions creates obstacles to precisely analyze the (un)boundedness of the operator. To us, the second issue is more crucial and distinguishes the problem on
![]() $\mathbb G^n$
from other settings like the Hartogs triangle. Actually, this issue leads to an interesting yet nontrivial weighted inequality problem in harmonic analysis. We elaborate below using a simple analogical example:
$\mathbb G^n$
from other settings like the Hartogs triangle. Actually, this issue leads to an interesting yet nontrivial weighted inequality problem in harmonic analysis. We elaborate below using a simple analogical example:
Let T be a singular integral operator on
![]() $L^p(\mathbb R^2)$
. Set
$L^p(\mathbb R^2)$
. Set
For which p is the operator T bounded on
![]() $L^p_{\text {anti}}(\mathbb R^2,|x_1-x_2|^a)$
?
$L^p_{\text {anti}}(\mathbb R^2,|x_1-x_2|^a)$
?
From the classical weighted theory, the singularity of the weight function
![]() $|x_1-x_2|^a$
over the line
$|x_1-x_2|^a$
over the line
![]() $\{x_1=x_2\}$
may cause unboundedness issue for T over
$\{x_1=x_2\}$
may cause unboundedness issue for T over
![]() $L^p(\mathbb R^2,|x_1-x_2|^a)$
. On the other hand, the antisymmetry property
$L^p(\mathbb R^2,|x_1-x_2|^a)$
. On the other hand, the antisymmetry property
![]() $f(x_1,x_2)=-f(x_2,x_1)$
implies that for any
$f(x_1,x_2)=-f(x_2,x_1)$
implies that for any
![]() $U\subseteq \mathbb R,$
$U\subseteq \mathbb R,$
suggesting possible better behavior of T on the subspace
![]() $L^p_{\text {anti}}(\mathbb R^2,|x_1-x_2|^a)$
than on the entire weighted
$L^p_{\text {anti}}(\mathbb R^2,|x_1-x_2|^a)$
than on the entire weighted
![]() $L^p$
space. Nevertheless, the usual harmonic analysis methods for weighted
$L^p$
space. Nevertheless, the usual harmonic analysis methods for weighted
![]() $L^p$
cannot be directly applied to this subspace case.
$L^p$
cannot be directly applied to this subspace case.
In this article, we overcome these issues on
![]() $\mathbb G^n$
and give the precise
$\mathbb G^n$
and give the precise
![]() $L^p$
regular range for
$L^p$
regular range for
![]() $P_{\mathbb G^n}$
and
$P_{\mathbb G^n}$
and
![]() $P^+_{\mathbb G^n}$
:
$P^+_{\mathbb G^n}$
:
Theorem 1.1
![]() $P_{\mathbb G^n}$
and
$P_{\mathbb G^n}$
and
![]() $P^+_{\mathbb G^n}$
are
$P^+_{\mathbb G^n}$
are
![]() $L^p$
bounded if and only if
$L^p$
bounded if and only if
![]() $p\in (\frac {2n}{n+1},\frac {2n}{n-1})$
.
$p\in (\frac {2n}{n+1},\frac {2n}{n-1})$
.
When
![]() $n=2$
,
$n=2$
,
![]() $P_{\mathbb G}$
is
$P_{\mathbb G}$
is
![]() $L^p$
bounded if and only if
$L^p$
bounded if and only if
![]() $p\in (\frac {4}{3},4)$
. In contrast to this result, Dall’Ara and Monguzzi [Reference Dall’Ara and MonguzziDM23] recently showed that, if one replaces
$p\in (\frac {4}{3},4)$
. In contrast to this result, Dall’Ara and Monguzzi [Reference Dall’Ara and MonguzziDM23] recently showed that, if one replaces
![]() $\mathbb D^2$
by unit ball
$\mathbb D^2$
by unit ball
![]() $\mathbb B_2$
in (1.4), the Bergman projection over the newly formed domain
$\mathbb B_2$
in (1.4), the Bergman projection over the newly formed domain
![]() $\{(w_1+w_2, w_1w_2):(w_1,w_2)\in \mathbb B_2\}$
will possess completely different
$\{(w_1+w_2, w_1w_2):(w_1,w_2)\in \mathbb B_2\}$
will possess completely different
![]() $L^p$
mapping properties. In particular, they proved the following:
$L^p$
mapping properties. In particular, they proved the following:
Set
![]() $D_{2^k}:=\{(w_1^{2^k}+w_2^{2^k}, w_1w_2):(w_1,w_2)\in \mathbb B_2\}$
with
$D_{2^k}:=\{(w_1^{2^k}+w_2^{2^k}, w_1w_2):(w_1,w_2)\in \mathbb B_2\}$
with
![]() $k\in \mathbb N\cup \{0\}$
. Then the Bergman projection on
$k\in \mathbb N\cup \{0\}$
. Then the Bergman projection on
![]() $D_{2^k}$
is
$D_{2^k}$
is
![]() $L^p$
bounded for all
$L^p$
bounded for all
![]() $p\in (1,\infty )$
.
$p\in (1,\infty )$
.
Our computations suggest that the distinction between results on
![]() $\mathbb G$
and
$\mathbb G$
and
![]() $D_{2^k}$
is caused by the product structure of
$D_{2^k}$
is caused by the product structure of
![]() $\mathbb D^2$
. It is yet to be investigated on what exact geometric property of these domains will determine the
$\mathbb D^2$
. It is yet to be investigated on what exact geometric property of these domains will determine the
![]() $L^p$
mapping behaviors of the projection over them.
$L^p$
mapping behaviors of the projection over them.
Our proof strategy of Theorems 1.1 can be summarized as follows:
-
(1) Similar to [Reference Chen, Jin and YuanCJY20, Reference Chen, Krantz and YuanCKY20], we reformulate Theorem 1.1 into a weighted
 $L^p$
regularity result of
$L^p$
regularity result of
 $P_{\mathbb D^n}$
for antisymmetric functions on the polydisc
$P_{\mathbb D^n}$
for antisymmetric functions on the polydisc
 $\mathbb D^n$
(see Theorems 2.4 and 2.3).
$\mathbb D^n$
(see Theorems 2.4 and 2.3). -
(2) We prove in detail the
 $L^p$
boundedness results for
$L^p$
boundedness results for
 $p\in (\frac {2n}{n+1},\frac {2n}{n-1})$
using known weighted estimates on the polydisc (see Theorem 2.3, Section 3, and [Reference Chen, Jin and YuanCJY23, Remark 1.5]).
$p\in (\frac {2n}{n+1},\frac {2n}{n-1})$
using known weighted estimates on the polydisc (see Theorem 2.3, Section 3, and [Reference Chen, Jin and YuanCJY23, Remark 1.5]). -
(3) To obtain the unboundedness result for the case
 $p=\frac {2n}{n-1}$
, we decompose
$p=\frac {2n}{n-1}$
, we decompose
 $P_{\mathbb D^n}$
into the sum of two operators
$P_{\mathbb D^n}$
into the sum of two operators
 $T^n_1$
and
$T^n_1$
and
 $T^n_2$
(see (4.5) and (4.6)), where
$T^n_2$
(see (4.5) and (4.6)), where
 $T^n_1=0$
and
$T^n_1=0$
and
 $T^n_2=P_{\mathbb D^n}$
over spaces of antisymmetric functions (see Lemmas 4.1 and 4.3).
$T^n_2=P_{\mathbb D^n}$
over spaces of antisymmetric functions (see Lemmas 4.1 and 4.3). -
(4) By using
 $T^n_2$
, we further reduce the (un)boundedness problem of
$T^n_2$
, we further reduce the (un)boundedness problem of
 $P_{\mathbb D^n}$
over a space of antisymmetric functions into a problem about an operator
$P_{\mathbb D^n}$
over a space of antisymmetric functions into a problem about an operator
 $\tilde T^n$
over a different space of symmetric functions. Finally, we provide examples for the unboundedness of
$\tilde T^n$
over a different space of symmetric functions. Finally, we provide examples for the unboundedness of
 $\tilde T^n$
there (see Theorems 4.2 and 4.4 and their proofs).
$\tilde T^n$
there (see Theorems 4.2 and 4.4 and their proofs).
We remark that the decomposition
![]() $P_{\mathbb D^n}=T^n_1+T^n_2$
is crucial in our proof. Using the kernel function of
$P_{\mathbb D^n}=T^n_1+T^n_2$
is crucial in our proof. Using the kernel function of
![]() $T^n_2$
, we are able to “cancel out” part of the weight of the space, transform the problem from an antisymmetric function space to a symmetric one, and reduce norm computation difficulty in n-dimensional case all at once.
$T^n_2$
, we are able to “cancel out” part of the weight of the space, transform the problem from an antisymmetric function space to a symmetric one, and reduce norm computation difficulty in n-dimensional case all at once.
Our article is organized as follows: In Section 2, we provide known lemmas and reduce
![]() $L^p$
estimates of
$L^p$
estimates of
![]() $P_{\mathbb G^n}$
and
$P_{\mathbb G^n}$
and
![]() $P^+_{\mathbb G^n}$
into weighted
$P^+_{\mathbb G^n}$
into weighted
![]() $L^p$
estimates of
$L^p$
estimates of
![]() $P_{\mathbb D^n}$
for (anti)symmetric functions. In Section 3, we recall the known weighted
$P_{\mathbb D^n}$
for (anti)symmetric functions. In Section 3, we recall the known weighted
![]() $L^p$
norm estimates of
$L^p$
norm estimates of
![]() $P_{\mathbb D}$
and give a detailed proof for the
$P_{\mathbb D}$
and give a detailed proof for the
![]() $L^p$
boundedness result for
$L^p$
boundedness result for
![]() $P_{\mathbb G^n}$
and
$P_{\mathbb G^n}$
and
![]() $P^+_{\mathbb G^n}$
. In Section 4, we present the decomposition of
$P^+_{\mathbb G^n}$
. In Section 4, we present the decomposition of
![]() $P_{\mathbb D^n}$
and examples for the
$P_{\mathbb D^n}$
and examples for the
![]() $L^p$
irregularity of
$L^p$
irregularity of
![]() $P_{\mathbb G^n}$
for
$P_{\mathbb G^n}$
for
![]() $p=\frac {2n}{n-1}$
. In Section 5, we point out some directions for future research.
$p=\frac {2n}{n-1}$
. In Section 5, we point out some directions for future research.
Given functions of several variables f and g, we use
![]() $f\lesssim g$
to denote that
$f\lesssim g$
to denote that
![]() $f\leq Cg$
for a constant C. If
$f\leq Cg$
for a constant C. If
![]() $f\lesssim g$
and
$f\lesssim g$
and
![]() $g\lesssim f$
, then we say f is comparable to g and write
$g\lesssim f$
, then we say f is comparable to g and write
![]() $f\approx g$
.
$f\approx g$
.
2 Pull back from
 $\mathbb G^n$
to
$\mathbb G^n$
to
 $\mathbb D^n$
$\mathbb D^n$
This section focuses on reformulating the
![]() $L^p$
regularity of
$L^p$
regularity of
![]() $P_{\mathbb G^n}$
into a problem on the polydisc
$P_{\mathbb G^n}$
into a problem on the polydisc
![]() ${\mathbb D}^n$
. Most of the lemmas and results were included in [Reference Chen, Jin and YuanCJY20, Reference Chen, Krantz and YuanCKY20]. We provide proofs here for completeness of our article.
${\mathbb D}^n$
. Most of the lemmas and results were included in [Reference Chen, Jin and YuanCJY20, Reference Chen, Krantz and YuanCKY20]. We provide proofs here for completeness of our article.
2.1 From
 $\mathbb G^n$
to
$\mathbb G^n$
to
 $\mathbb D^n$
$\mathbb D^n$
Recall that
![]() $\Phi _n(w)=(p_1(w),p_2(w),\dots ,p_n(w)),$
where
$\Phi _n(w)=(p_1(w),p_2(w),\dots ,p_n(w)),$
where
Then
![]() $\Phi _n$
is a ramified rational proper covering map of order
$\Phi _n$
is a ramified rational proper covering map of order
![]() $n!$
with complex holomorphic Jacobian
$n!$
with complex holomorphic Jacobian
(see, for example, [Reference Chen, Krantz and YuanCKY20]). Let
![]() $h\in L^p(\mathbb G^n)$
. Via a change of variables, the estimate
$h\in L^p(\mathbb G^n)$
. Via a change of variables, the estimate
is equivalent to
Using the Bell’s transformation formula [Reference BellBel81],
(2.1) becomes the following weighted estimate:
By Bell’s transformation formula for the Bergman kernel,
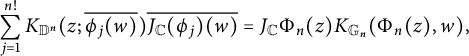 $$\begin{align*}\sum_{j=1}^{n!}K_{\mathbb D^n}(z; \overline {\phi_j(w)})\overline {J_{\mathbb C}(\phi_j)(w)}=J_{\mathbb C}\Phi_n(z)K_{\mathbb G_n}(\Phi_n(z),w), \end{align*}$$
$$\begin{align*}\sum_{j=1}^{n!}K_{\mathbb D^n}(z; \overline {\phi_j(w)})\overline {J_{\mathbb C}(\phi_j)(w)}=J_{\mathbb C}\Phi_n(z)K_{\mathbb G_n}(\Phi_n(z),w), \end{align*}$$
where
![]() $\phi _j$
are the
$\phi _j$
are the
![]() $n!$
local inverses of
$n!$
local inverses of
![]() $\Phi $
. Therefore, to show the estimate
$\Phi $
. Therefore, to show the estimate
it is sufficient to prove that
Let
![]() $\mathcal S_n$
denote the family of all permutations of
$\mathcal S_n$
denote the family of all permutations of
![]() $\{z_1,\dots ,z_n\}$
. Since
$\{z_1,\dots ,z_n\}$
. Since
![]() $\Phi _n$
is invariant under any permutation, the function
$\Phi _n$
is invariant under any permutation, the function
![]() $h\circ \Phi _n$
also inherits symmetry properties. To clearly describe them, we give several definitions below. For
$h\circ \Phi _n$
also inherits symmetry properties. To clearly describe them, we give several definitions below. For
![]() $j,k\in \{1,\dots ,n\}$
with
$j,k\in \{1,\dots ,n\}$
with
![]() $j<k$
, we let
$j<k$
, we let
![]() $\tau _{j,k}$
denote the 2-cycle in
$\tau _{j,k}$
denote the 2-cycle in
![]() $\mathcal S_n$
that interchanges
$\mathcal S_n$
that interchanges
![]() $z_j$
and
$z_j$
and
![]() $z_k$
. For
$z_k$
. For
![]() $j=1,\dots ,n$
, we will also abuse the notation for
$j=1,\dots ,n$
, we will also abuse the notation for
![]() $\tau \in \mathcal S_n$
and let
$\tau \in \mathcal S_n$
and let
![]() $\tau (j)$
denote the index such that
$\tau (j)$
denote the index such that
![]() $\tau (z_j)=z_{\tau (j)}$
.
$\tau (z_j)=z_{\tau (j)}$
.
Definition 2.1 Let f be a function on
![]() $\mathbb D^n$
.
$\mathbb D^n$
.
-
(1) f is called
 $(j,k)$
symmetric if
$(j,k)$
symmetric if
 $f(z_1,\dots ,z_n)=f\circ \tau _{j,k}(z_1,\dots ,z_n)$
, and is called symmetric if
$f(z_1,\dots ,z_n)=f\circ \tau _{j,k}(z_1,\dots ,z_n)$
, and is called symmetric if
 $f(z_1,\dots ,z_n)=f\circ \tau _{j,k}(z_1,\dots ,z_n)$
for any
$f(z_1,\dots ,z_n)=f\circ \tau _{j,k}(z_1,\dots ,z_n)$
for any
 $j\neq k$
.
$j\neq k$
. -
(2) f is called
 $(j,k)$
antisymmetric if
$(j,k)$
antisymmetric if
 $f(z_1,\dots ,z_n)=-f\circ \tau _{j,k}(z_1,\dots ,z_n)$
and is called antisymmetric if
$f(z_1,\dots ,z_n)=-f\circ \tau _{j,k}(z_1,\dots ,z_n)$
and is called antisymmetric if
 $f(z_1,\dots ,z_n)=-f\circ \tau _{j,k}(z_1,\dots ,z_n)$
for any
$f(z_1,\dots ,z_n)=-f\circ \tau _{j,k}(z_1,\dots ,z_n)$
for any
 $j\neq k$
.
$j\neq k$
.
By the above definition,
![]() $h\circ \Phi _n$
is symmetric while
$h\circ \Phi _n$
is symmetric while
![]() $J_{\mathbb C}\Phi _n$
is antisymmetric. Therefore, the function
$J_{\mathbb C}\Phi _n$
is antisymmetric. Therefore, the function
![]() $J_{\mathbb C}\Phi _n\cdot h\circ \Phi _n$
is antisymmetric and
$J_{\mathbb C}\Phi _n\cdot h\circ \Phi _n$
is antisymmetric and
![]() $|J_{\mathbb C}\Phi _n|\cdot h\circ \Phi _n$
is symmetric. It’s also not hard to see that
$|J_{\mathbb C}\Phi _n|\cdot h\circ \Phi _n$
is symmetric. It’s also not hard to see that
![]() $P_{\mathbb D^n}(J_{\mathbb C}\Phi _n\cdot (h\circ \Phi _n))$
and
$P_{\mathbb D^n}(J_{\mathbb C}\Phi _n\cdot (h\circ \Phi _n))$
and
![]() $P^+_{\mathbb D^n}(J_{\mathbb C}\Phi _n\cdot (h\circ \Phi _n))$
are antisymmetric and
$P^+_{\mathbb D^n}(J_{\mathbb C}\Phi _n\cdot (h\circ \Phi _n))$
are antisymmetric and
![]() $P^+_{\mathbb D^n}(|J_{\mathbb C}\Phi _n|\cdot (h\circ \Phi _n))$
is symmetric. Set
$P^+_{\mathbb D^n}(|J_{\mathbb C}\Phi _n|\cdot (h\circ \Phi _n))$
is symmetric. Set
![]() $L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
and
$L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
and
![]() $L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
turn out to be equivalent to
$L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
turn out to be equivalent to
![]() $L^p(\mathbb G^n)$
.
$L^p(\mathbb G^n)$
.
The next lemma gives the norm equivalence of
![]() $L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
,
$L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
,
![]() $L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
, and
$L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
, and
![]() $L^p(\mathbb G^n)$
. When
$L^p(\mathbb G^n)$
. When
![]() $p=2$
, this lemma can be viewed as a special case of [Reference TrybulaTry13, Theorem 1].
$p=2$
, this lemma can be viewed as a special case of [Reference TrybulaTry13, Theorem 1].
Lemma 2.2 The following statements are true:
-
(1)
 $L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
is norm equivalent to
$L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
is norm equivalent to
 $L^p(\mathbb G^n)$
via the mapping: (2.6)
$L^p(\mathbb G^n)$
via the mapping: (2.6) $$ \begin{align} f\mapsto \sum_{j=1}^{n!}\left(\frac{f}{J_{\mathbb C}\Phi}\right)\circ \phi_j. \end{align} $$
$$ \begin{align} f\mapsto \sum_{j=1}^{n!}\left(\frac{f}{J_{\mathbb C}\Phi}\right)\circ \phi_j. \end{align} $$
-
(2)
 $L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
is norm equivalent to
$L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
is norm equivalent to
 $L^p(\mathbb G^n)$
via the mapping: (2.7)
$L^p(\mathbb G^n)$
via the mapping: (2.7) $$ \begin{align}f\mapsto \sum_{j=1}^{n!}\left(\frac{f}{|J_{\mathbb C}\Phi_n|}\right)\circ \phi_j. \end{align} $$
$$ \begin{align}f\mapsto \sum_{j=1}^{n!}\left(\frac{f}{|J_{\mathbb C}\Phi_n|}\right)\circ \phi_j. \end{align} $$
Proof We prove the statement for
![]() $L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
. The proof for
$L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
. The proof for
![]() $L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
is similar. We begin by showing that the mapping in (2.6) is norm preserving. Since f is antisymmetric, the function
$L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
is similar. We begin by showing that the mapping in (2.6) is norm preserving. Since f is antisymmetric, the function
![]() $\frac {f}{J_{\mathbb C}\Phi _n}$
is symmetric. Thus,
$\frac {f}{J_{\mathbb C}\Phi _n}$
is symmetric. Thus,
![]() $\left (\frac {f}{J_{\mathbb C}\Phi _n}\right )\circ \phi _j=\left (\frac {f}{J_{\mathbb C}\Phi _n}\right )\circ \phi _k$
for any
$\left (\frac {f}{J_{\mathbb C}\Phi _n}\right )\circ \phi _j=\left (\frac {f}{J_{\mathbb C}\Phi _n}\right )\circ \phi _k$
for any
![]() $j,k$
and
$j,k$
and
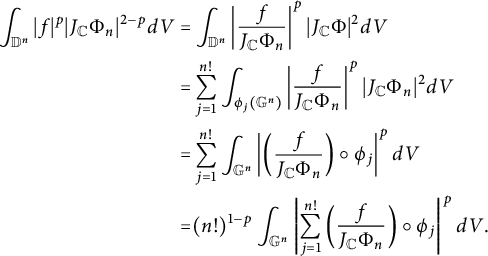 $$ \begin{align*}\int_{\mathbb D^n}|f|^p|J_{\mathbb C}\Phi_n|^{2-p}dV=&\int_{\mathbb D^n}\left|\frac{f}{J_{\mathbb C}\Phi_n}\right|^p|J_{\mathbb C}\Phi|^{2}dV\\=&\sum_{j=1}^{n!}\int_{\phi_j(\mathbb G^n)}\left|\frac{f}{J_{\mathbb C}\Phi_n}\right|^p|J_{\mathbb C}\Phi_n|^{2}dV\\=&\sum_{j=1}^{n!}\int_{\mathbb G^n}\left|\left(\frac{f}{J_{\mathbb C}\Phi_n}\right)\circ \phi_j\right|^pdV\\=&(n!)^{1-p}\int_{\mathbb G^n}\left|\sum_{j=1}^{n!}\left(\frac{f}{J_{\mathbb C}\Phi_n}\right)\circ \phi_j\right|^pdV.\end{align*} $$
$$ \begin{align*}\int_{\mathbb D^n}|f|^p|J_{\mathbb C}\Phi_n|^{2-p}dV=&\int_{\mathbb D^n}\left|\frac{f}{J_{\mathbb C}\Phi_n}\right|^p|J_{\mathbb C}\Phi|^{2}dV\\=&\sum_{j=1}^{n!}\int_{\phi_j(\mathbb G^n)}\left|\frac{f}{J_{\mathbb C}\Phi_n}\right|^p|J_{\mathbb C}\Phi_n|^{2}dV\\=&\sum_{j=1}^{n!}\int_{\mathbb G^n}\left|\left(\frac{f}{J_{\mathbb C}\Phi_n}\right)\circ \phi_j\right|^pdV\\=&(n!)^{1-p}\int_{\mathbb G^n}\left|\sum_{j=1}^{n!}\left(\frac{f}{J_{\mathbb C}\Phi_n}\right)\circ \phi_j\right|^pdV.\end{align*} $$
Note also that
![]() $h\mapsto \frac {1}{n!}J_{\mathbb C}\Phi _n\cdot h\circ \Phi _n$
is the inverse of (2.6), the mapping in (2.6) is onto which completes the proof.
$h\mapsto \frac {1}{n!}J_{\mathbb C}\Phi _n\cdot h\circ \Phi _n$
is the inverse of (2.6), the mapping in (2.6) is onto which completes the proof.
By Lemma 2.2 and the fact that
![]() $|P_{\mathbb G^n}(f)(z)|\leq P^+_{\mathbb G^n}(|f|)(z)$
, the next two theorems are sufficient to yield Theorem 1.1.
$|P_{\mathbb G^n}(f)(z)|\leq P^+_{\mathbb G^n}(|f|)(z)$
, the next two theorems are sufficient to yield Theorem 1.1.
Theorem 2.3
![]() $P_{\mathbb D^n}$
and
$P_{\mathbb D^n}$
and
![]() $P^+_{\mathbb D^n}$
are bounded on
$P^+_{\mathbb D^n}$
are bounded on
![]() $L^p(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
for
$L^p(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
for
![]() $p\in \left (\frac {2n}{n+1}, \frac {2n}{n-1}\right )$
.
$p\in \left (\frac {2n}{n+1}, \frac {2n}{n-1}\right )$
.
Theorem 2.3 appears as [Reference Chen, Jin and YuanCJY23, Remark 1.5] with the same range of p.
Theorem 2.4
![]() $P_{\mathbb D^n}$
is unbounded on
$P_{\mathbb D^n}$
is unbounded on
![]() $L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
for
$L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
for
![]() $p=\frac {2n}{n-1}$
.
$p=\frac {2n}{n-1}$
.
Last, we reference below the Forelli–Rudin estimates on
![]() $\mathbb D$
which will be used in the proof of Theorem 2.4 (see, for example, [Reference ZhuZhu05] for its proof).
$\mathbb D$
which will be used in the proof of Theorem 2.4 (see, for example, [Reference ZhuZhu05] for its proof).
Lemma 2.5 (Forelli–Rudin)
For
![]() $\epsilon <1$
and
$\epsilon <1$
and
![]() $z\in \mathbb D$
, let
$z\in \mathbb D$
, let
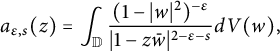 $$ \begin{align} a_{\epsilon,s}(z)=\int_{\mathbb D}\frac{(1-|w|^2)^{-\epsilon}}{|1-z\bar w |^{2-\epsilon-s}}dV(w), \end{align} $$
$$ \begin{align} a_{\epsilon,s}(z)=\int_{\mathbb D}\frac{(1-|w|^2)^{-\epsilon}}{|1-z\bar w |^{2-\epsilon-s}}dV(w), \end{align} $$
Then:
-
(1) for
 $s>0$
,
$s>0$
,
 $a_{\epsilon ,s}(z)$
is bounded on
$a_{\epsilon ,s}(z)$
is bounded on
 $\mathbb D$
;
$\mathbb D$
; -
(2) for
 $s=0$
,
$s=0$
,
 $a_{\epsilon ,s}(z)$
is comparable to the function
$a_{\epsilon ,s}(z)$
is comparable to the function
 $-\log (1-|z|^2)$
;
$-\log (1-|z|^2)$
; -
(3) for
 $s<0$
,
$s<0$
,
 $a_{\epsilon ,s}(z)$
is comparable to the function
$a_{\epsilon ,s}(z)$
is comparable to the function
 $(1-|z|^2)^{s}$
.
$(1-|z|^2)^{s}$
.
3 Proof of Theorem 2.3
While [Reference Chen, Jin and YuanCJY23, Remark 1.5] sketches the proof of Theorem 2.3, here we provide all the relevant details to make the article self-contained (see also [Reference Zhang and YuanZY, Corollary 6.1]). The main ingredient of the weighted norm estimates of the positive Bergman operator
![]() $P^+_{\mathbb D}$
over weighted
$P^+_{\mathbb D}$
over weighted
![]() $L^p$
spaces. On the unit disc
$L^p$
spaces. On the unit disc
![]() $\mathbb D$
, the boundedness of
$\mathbb D$
, the boundedness of
![]() $P_{\mathbb D}$
and
$P_{\mathbb D}$
and
![]() $P^+_{\mathbb D}$
on weighted
$P^+_{\mathbb D}$
on weighted
![]() $L^p$
spaces is closely related to the Bekollé–Bonami constant of weight functions. Let
$L^p$
spaces is closely related to the Bekollé–Bonami constant of weight functions. Let
![]() $T_z$
denote the Carleson tent over z in the unit disc
$T_z$
denote the Carleson tent over z in the unit disc
![]() $\mathbb D$
defined as below:
$\mathbb D$
defined as below:
-
•
 $T_z:=\left \{w\in \mathbb D:\left |1-\bar w\frac {z}{|z|}\right |<1-|z|\right \}$
for
$T_z:=\left \{w\in \mathbb D:\left |1-\bar w\frac {z}{|z|}\right |<1-|z|\right \}$
for
 $z\neq 0$
, and
$z\neq 0$
, and -
•
 $T_z:= \mathbb D$
for
$T_z:= \mathbb D$
for
 $z=0$
.
$z=0$
.
Bekollé and Bonami [Reference Bekollé and BonamiBB78] characterized weighted
![]() $L^p$
spaces where
$L^p$
spaces where
![]() $P_{\mathbb D}$
and
$P_{\mathbb D}$
and
![]() $P^+_{\mathbb D}$
are bounded:
$P^+_{\mathbb D}$
are bounded:
Theorem 3.1 (Bekollé–Bonami [Reference Bekollé and BonamiBB78])
Let the weight
![]() $u(w)$
be a positive, locally integrable function on the unit disc
$u(w)$
be a positive, locally integrable function on the unit disc
![]() $\mathbb D$
. Let
$\mathbb D$
. Let
![]() $1<p<\infty $
. Then the following conditions are equivalent:
$1<p<\infty $
. Then the following conditions are equivalent:
-
(1)
 $P:L^p(\mathbb D,u)\mapsto L^p(\mathbb D,u)$
is bounded.
$P:L^p(\mathbb D,u)\mapsto L^p(\mathbb D,u)$
is bounded. -
(2)
 $P^+:L^p(\mathbb D,u)\mapsto L^p(\mathbb D,u)$
is bounded.
$P^+:L^p(\mathbb D,u)\mapsto L^p(\mathbb D,u)$
is bounded. -
(3) The Bekollé–Bonami constant
is finite. $$ \begin{align*} B_p(u):=\sup_{z\in \mathbb D}\frac{\int_{T_z}u(w) dV(w)}{\int_{T_z}dV(w)}\left(\frac{\int_{T_z}u^{-\frac{1}{p-1}} (w)dV(w)}{\int_{T_z}dV(w)}\right)^{p-1} \end{align*} $$
$$ \begin{align*} B_p(u):=\sup_{z\in \mathbb D}\frac{\int_{T_z}u(w) dV(w)}{\int_{T_z}dV(w)}\left(\frac{\int_{T_z}u^{-\frac{1}{p-1}} (w)dV(w)}{\int_{T_z}dV(w)}\right)^{p-1} \end{align*} $$
Using dyadic harmonic analysis technique, various authors established quantitative weighted
![]() $L^p$
norm estimates of the Bergman projection (see [Reference Huo and WickHW20b, Reference Huo, Wagner and WickHWW21, Reference Pott and RegueraPR13, Reference Rahm, Tchoundja and WickRTW17]).
$L^p$
norm estimates of the Bergman projection (see [Reference Huo and WickHW20b, Reference Huo, Wagner and WickHWW21, Reference Pott and RegueraPR13, Reference Rahm, Tchoundja and WickRTW17]).
Theorem 3.2 [Reference Rahm, Tchoundja and WickRTW17, Lemma 15]
Let the weight function u be positive, locally integrable on
![]() $\mathbb D$
. Then for
$\mathbb D$
. Then for
![]() $p\in (1,\infty )$
,
$p\in (1,\infty )$
,
Lemma 3.3 For a fixed point
![]() $a\in \mathbb D$
, let
$a\in \mathbb D$
, let
![]() $u_p(w)=|a-w|^{2-p}$
. Then for any
$u_p(w)=|a-w|^{2-p}$
. Then for any
![]() $p\in (4/3,4)$
,
$p\in (4/3,4)$
,
![]() $B_p(u_p)\lesssim 1,$
where the upper bound is independent of a. Moreover, if we choose arbitrary m points
$B_p(u_p)\lesssim 1,$
where the upper bound is independent of a. Moreover, if we choose arbitrary m points
![]() $a_1,\dots ,a_m$
in
$a_1,\dots ,a_m$
in
![]() $\mathbb D$
, and set
$\mathbb D$
, and set
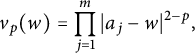 $$ \begin{align*}v_p(w)=\prod_{j=1}^{m}|a_j-w|^{2-p},\end{align*} $$
$$ \begin{align*}v_p(w)=\prod_{j=1}^{m}|a_j-w|^{2-p},\end{align*} $$
then for any
![]() $p\in (\frac {2m+2}{m+2},\frac {2m+2}{m})$
,
$p\in (\frac {2m+2}{m+2},\frac {2m+2}{m})$
,
![]() $B_p(v_p)\lesssim 1$
. Here, the upper bounds may depend on constants m and p but are independent of
$B_p(v_p)\lesssim 1$
. Here, the upper bounds may depend on constants m and p but are independent of
![]() $a_j$
.
$a_j$
.
Proof We first consider the case of the weight
![]() $u_p$
. Note that
$u_p$
. Note that
![]() $u_p$
and
$u_p$
and
![]() $u_p^{-1/(p-1)}$
are integrable on
$u_p^{-1/(p-1)}$
are integrable on
![]() $\mathbb D$
if and only if
$\mathbb D$
if and only if
![]() $p\in (\frac {4}{3},4)$
. Then, it is enough to show that
$p\in (\frac {4}{3},4)$
. Then, it is enough to show that
![]() $B_p(|a-w|^{b})\lesssim 1$
with an upper bound independent of a if both
$B_p(|a-w|^{b})\lesssim 1$
with an upper bound independent of a if both
![]() $u_p$
and
$u_p$
and
![]() $u_p^{-1/(p-1)}$
are integrable on
$u_p^{-1/(p-1)}$
are integrable on
![]() $\mathbb D$
. We consider the integral of
$\mathbb D$
. We consider the integral of
![]() $u_p$
and
$u_p$
and
![]() $u_p^{-1/(p-1)}$
over
$u_p^{-1/(p-1)}$
over
![]() $T_z$
for arbitrary
$T_z$
for arbitrary
![]() $z\in \mathbb D$
. Notice that
$z\in \mathbb D$
. Notice that
![]() $T_z=\mathbb D\cap \{w:|w-\frac {z}{|z|}|<1-|z|\}$
is the intersection set of the unit disc
$T_z=\mathbb D\cap \{w:|w-\frac {z}{|z|}|<1-|z|\}$
is the intersection set of the unit disc
![]() $\mathbb D$
and the disc centered at the point
$\mathbb D$
and the disc centered at the point
![]() $z/|z|$
with Euclidean radius
$z/|z|$
with Euclidean radius
![]() $1 -|z|$
. A geometric consideration then yields that the Lebesgue measure
$1 -|z|$
. A geometric consideration then yields that the Lebesgue measure
![]() $V(T_z)$
of
$V(T_z)$
of
![]() $T_z$
is comparable to
$T_z$
is comparable to
![]() $(1-|z|)^2$
.
$(1-|z|)^2$
.
If
![]() $|a-z|<3(1-|z|)$
, then
$|a-z|<3(1-|z|)$
, then
![]() $T_z$
is contained in a ball
$T_z$
is contained in a ball
![]() $B_a$
given by
$B_a$
given by
Thus,
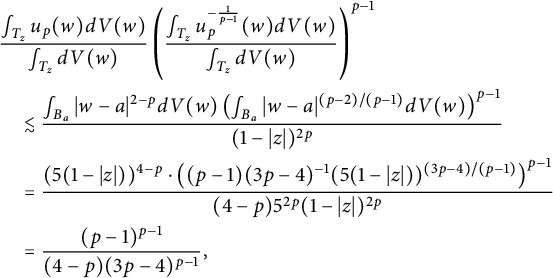 $$ \begin{align*} &\frac{\int_{T_z}u_p(w) dV(w)}{\int_{T_z}dV(w)}\left(\frac{\int_{T_z}u_p^{-\frac{1}{p-1}} (w)dV(w)}{\int_{T_z}dV(w)}\right)^{p-1}\\&\quad \lesssim \frac{\int_{B_a}|w-a|^{2-p} dV(w)\left(\int_{B_a}|w-a|^{(p-2)/(p-1)} dV(w)\right)^{p-1}}{(1-|z|)^{2p}}\\&\quad =\frac{(5(1-|z|))^{4-p}\cdot \left((p-1)(3p-4)^{-1}(5(1-|z|))^{(3p-4)/(p-1)}\right)^{p-1}}{(4-p)5^{2p}(1-|z|)^{2p}}\\&\quad =\frac{(p-1)^{p-1}}{(4-p)(3p-4)^{p-1}}, \end{align*} $$
$$ \begin{align*} &\frac{\int_{T_z}u_p(w) dV(w)}{\int_{T_z}dV(w)}\left(\frac{\int_{T_z}u_p^{-\frac{1}{p-1}} (w)dV(w)}{\int_{T_z}dV(w)}\right)^{p-1}\\&\quad \lesssim \frac{\int_{B_a}|w-a|^{2-p} dV(w)\left(\int_{B_a}|w-a|^{(p-2)/(p-1)} dV(w)\right)^{p-1}}{(1-|z|)^{2p}}\\&\quad =\frac{(5(1-|z|))^{4-p}\cdot \left((p-1)(3p-4)^{-1}(5(1-|z|))^{(3p-4)/(p-1)}\right)^{p-1}}{(4-p)5^{2p}(1-|z|)^{2p}}\\&\quad =\frac{(p-1)^{p-1}}{(4-p)(3p-4)^{p-1}}, \end{align*} $$
provided
![]() $u_p$
and
$u_p$
and
![]() $u_p^{-1/(p-1)}$
are integrable. If
$u_p^{-1/(p-1)}$
are integrable. If
![]() $|a-z|\geq 3(1-|z|)$
, then
$|a-z|\geq 3(1-|z|)$
, then
![]() $ |a-w|\approx |a-z|$
for all
$ |a-w|\approx |a-z|$
for all
![]() $w\in T_z$
and hence
$w\in T_z$
and hence
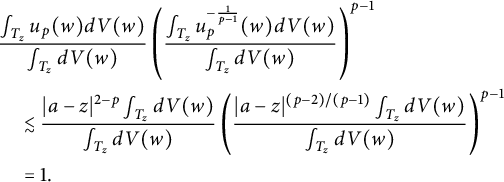 $$ \begin{align*} &\frac{\int_{T_z}u_p(w) dV(w)}{\int_{T_z}dV(w)}\left(\frac{\int_{T_z}u_p^{-\frac{1}{p-1}} (w)dV(w)}{\int_{T_z}dV(w)}\right)^{p-1}\\& \quad \lesssim \frac{|a-z|^{2-p}\int_{T_z} dV(w)}{\int_{T_z}dV(w)}\left(\frac{|a-z|^{(p-2)/(p-1)}\int_{T_z} dV(w)}{\int_{T_z}dV(w)}\right)^{p-1}\\& \quad =1. \end{align*} $$
$$ \begin{align*} &\frac{\int_{T_z}u_p(w) dV(w)}{\int_{T_z}dV(w)}\left(\frac{\int_{T_z}u_p^{-\frac{1}{p-1}} (w)dV(w)}{\int_{T_z}dV(w)}\right)^{p-1}\\& \quad \lesssim \frac{|a-z|^{2-p}\int_{T_z} dV(w)}{\int_{T_z}dV(w)}\left(\frac{|a-z|^{(p-2)/(p-1)}\int_{T_z} dV(w)}{\int_{T_z}dV(w)}\right)^{p-1}\\& \quad =1. \end{align*} $$
Since the upper bound obtained in both cases are independent of the choice of a and
![]() $T_z$
, we conclude that
$T_z$
, we conclude that
![]() $B_p(u_p)$
is bounded above by a constant if and only if
$B_p(u_p)$
is bounded above by a constant if and only if
![]() $p\in (4/3,4)$
and the upper bound is independent of
$p\in (4/3,4)$
and the upper bound is independent of
![]() $a_j$
.
$a_j$
.
Now we turn to the case of weight
![]() $v_p(w)=\prod _{j=1}^{m}|a_j-w|^{2-p}$
. By a similar proof as above,
$v_p(w)=\prod _{j=1}^{m}|a_j-w|^{2-p}$
. By a similar proof as above,
![]() $B_p(|a-w|^{(2-p)m})\lesssim 1$
for any
$B_p(|a-w|^{(2-p)m})\lesssim 1$
for any
![]() $p\in (\frac {2m+2}{m+2},\frac {2m+2}{m})$
where the upper bound is independent of a. Using Hölder’s inequality, we obtain for any
$p\in (\frac {2m+2}{m+2},\frac {2m+2}{m})$
where the upper bound is independent of a. Using Hölder’s inequality, we obtain for any
![]() $z\in \mathbb D$
$z\in \mathbb D$
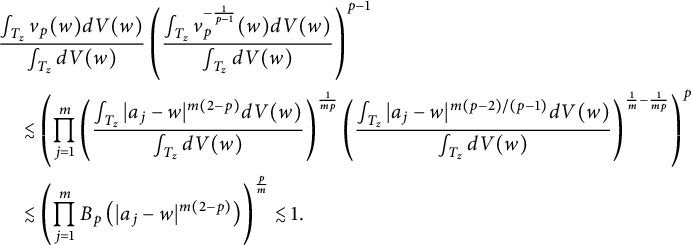 $$ \begin{align*} &\frac{\int_{T_z}v_p(w) dV(w)}{\int_{T_z}dV(w)}\left(\frac{\int_{T_z}v_p^{-\frac{1}{p-1}} (w)dV(w)}{\int_{T_z}dV(w)}\right)^{p-1}\\& \quad \lesssim \left(\prod_{j=1}^{m}\left(\frac{\int_{T_z} |a_j-w|^{m(2-p)}dV(w)}{\int_{T_z}dV(w)}\right)^{\frac{1}{mp}}\left(\frac{\int_{T_z} |a_j-w|^{m(p-2)/(p-1)}dV(w)}{\int_{T_z}dV(w)}\right)^{\frac{1}{m}-\frac{1}{mp}}\right)^p\\& \quad \lesssim \left(\prod_{j=1}^{m}B_p\left(|a_j-w|^{m(2-p)}\right)\right)^{\frac{p}{m}}\lesssim 1. \end{align*} $$
$$ \begin{align*} &\frac{\int_{T_z}v_p(w) dV(w)}{\int_{T_z}dV(w)}\left(\frac{\int_{T_z}v_p^{-\frac{1}{p-1}} (w)dV(w)}{\int_{T_z}dV(w)}\right)^{p-1}\\& \quad \lesssim \left(\prod_{j=1}^{m}\left(\frac{\int_{T_z} |a_j-w|^{m(2-p)}dV(w)}{\int_{T_z}dV(w)}\right)^{\frac{1}{mp}}\left(\frac{\int_{T_z} |a_j-w|^{m(p-2)/(p-1)}dV(w)}{\int_{T_z}dV(w)}\right)^{\frac{1}{m}-\frac{1}{mp}}\right)^p\\& \quad \lesssim \left(\prod_{j=1}^{m}B_p\left(|a_j-w|^{m(2-p)}\right)\right)^{\frac{p}{m}}\lesssim 1. \end{align*} $$
Therefore,
![]() $B_p(v_p)\lesssim 1$
with upper bound independent of points
$B_p(v_p)\lesssim 1$
with upper bound independent of points
![]() $a_j$
.
$a_j$
.
With Lemma 3.3, we are ready to show Theorem 2.3:
Proof of Theorem 2.3
Since
![]() $|P_{\mathbb D^n}(h)(z)|\leq P^+_{\mathbb D^n}(|h|)(z)$
for any
$|P_{\mathbb D^n}(h)(z)|\leq P^+_{\mathbb D^n}(|h|)(z)$
for any
![]() $h\in L^p(\mathbb D^n, |J_{\mathbb C}\Phi _n|^{2-p})$
, it suffices to show the boundedness for
$h\in L^p(\mathbb D^n, |J_{\mathbb C}\Phi _n|^{2-p})$
, it suffices to show the boundedness for
![]() $P^+_{\mathbb D^n}$
. Note that
$P^+_{\mathbb D^n}$
. Note that
![]() $J_{\mathbb C}\Phi _n(w)$
consists of
$J_{\mathbb C}\Phi _n(w)$
consists of
![]() $n-1$
many factors of each variable
$n-1$
many factors of each variable
![]() $w_j$
. When integrating with respect to the single variable
$w_j$
. When integrating with respect to the single variable
![]() $w_j$
, only these
$w_j$
, only these
![]() $n-1$
factors matter in
$n-1$
factors matter in
![]() $J_{\mathbb C}\Phi _n(w)$
. Thus the boundedness of
$J_{\mathbb C}\Phi _n(w)$
. Thus the boundedness of
![]() $P^+_{\mathbb D^n}$
on
$P^+_{\mathbb D^n}$
on
![]() $L^p(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
for
$L^p(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
for
![]() $p\in \left (\frac {2n}{n+1}, \frac {2n}{n-1}\right )$
follows from Fubini and Lemma 3.3 with
$p\in \left (\frac {2n}{n+1}, \frac {2n}{n-1}\right )$
follows from Fubini and Lemma 3.3 with
![]() $m=n-1$
.
$m=n-1$
.
4 Proof of Theorem 2.4
We will first prove the theorem for the case
![]() $n=2$
, clearly illustrating the decomposition we use for
$n=2$
, clearly illustrating the decomposition we use for
![]() $P_{\mathbb D^2}$
. Then we dive into the case for general n where the decomposition procedure and estimations are more complicated yet the same strategy applies.
$P_{\mathbb D^2}$
. Then we dive into the case for general n where the decomposition procedure and estimations are more complicated yet the same strategy applies.
4.1 The case for
 $n=2$
$n=2$
Note that
![]() $J_{\mathbb C}\Phi _2=w_1-w_2$
. To prove Theorem 2.4, we consider the decomposition
$J_{\mathbb C}\Phi _2=w_1-w_2$
. To prove Theorem 2.4, we consider the decomposition
![]() $P_{\mathbb D^2}=T^2_1+T^2_2$
where
$P_{\mathbb D^2}=T^2_1+T^2_2$
where
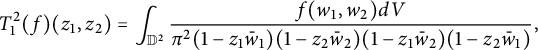 $$ \begin{align} T^2_1(f)(z_1,z_2)&=\int_{\mathbb D^2}\frac{f(w_1,w_2)dV}{\pi^2(1-z_1\bar w_1)(1-z_2\bar w_2)(1-z_1\bar w_2)(1-z_2\bar w_1)}, \end{align} $$
$$ \begin{align} T^2_1(f)(z_1,z_2)&=\int_{\mathbb D^2}\frac{f(w_1,w_2)dV}{\pi^2(1-z_1\bar w_1)(1-z_2\bar w_2)(1-z_1\bar w_2)(1-z_2\bar w_1)}, \end{align} $$
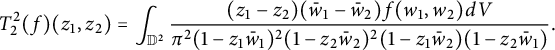 $$ \begin{align} T^2_2(f)(z_1,z_2)&=\int_{\mathbb D^2}\frac{(z_1-z_2)(\bar w_1-\bar w_2)f(w_1,w_2)dV}{\pi^2(1-z_1\bar w_1)^2(1-z_2\bar w_2)^2(1-z_1\bar w_2)(1-z_2\bar w_1)}. \end{align} $$
$$ \begin{align} T^2_2(f)(z_1,z_2)&=\int_{\mathbb D^2}\frac{(z_1-z_2)(\bar w_1-\bar w_2)f(w_1,w_2)dV}{\pi^2(1-z_1\bar w_1)^2(1-z_2\bar w_2)^2(1-z_1\bar w_2)(1-z_2\bar w_1)}. \end{align} $$
Lemma 4.1
![]() $T^2_1$
is a zero operator on
$T^2_1$
is a zero operator on
![]() $L^p_{\text {anti}}(\mathbb D^2,|w_1-w_2|^{2-p})$
.
$L^p_{\text {anti}}(\mathbb D^2,|w_1-w_2|^{2-p})$
.
Proof Note that
![]() $T^2_1(f)(z_1,z_2)$
is symmetric by its definition. For any
$T^2_1(f)(z_1,z_2)$
is symmetric by its definition. For any
![]() $f\in L^p_{\text {anti}}(\mathbb D^2, |w_1-w_2|^{2-p})$
,
$f\in L^p_{\text {anti}}(\mathbb D^2, |w_1-w_2|^{2-p})$
,
which implies
![]() $T^2_1(f)= 0$
.
$T^2_1(f)= 0$
.
By Lemma 4.1,
![]() $P_{\mathbb D^2}=T^2_2$
on
$P_{\mathbb D^2}=T^2_2$
on
![]() $L^p_{\text {anti}}(\mathbb D^2,|w_1-w_2|^{2-p})$
. So, Theorem 2.4 can be further reduced into the following statement in the case
$L^p_{\text {anti}}(\mathbb D^2,|w_1-w_2|^{2-p})$
. So, Theorem 2.4 can be further reduced into the following statement in the case
![]() $n=2$
.
$n=2$
.
Theorem 4.2
![]() $T^2_2$
is unbounded on
$T^2_2$
is unbounded on
![]() $L^p_{\text {anti}}(\mathbb D^2,|w_1-w_2|^{2-p})$
for
$L^p_{\text {anti}}(\mathbb D^2,|w_1-w_2|^{2-p})$
for
![]() $p=4=\frac {2\times 2}{2-1}$
.
$p=4=\frac {2\times 2}{2-1}$
.
Proof Let
![]() $\tilde T^2$
denote the operator given as follows:
$\tilde T^2$
denote the operator given as follows:
Then
 $$ \begin{align} \tilde T^2(h)(z)&=\int_{\mathbb D^2}\frac{(\bar w_1-\bar w_2)^2h(w)dV}{\pi^2(1-z_1\bar w_1)^2(1-z_2\bar w_2)^2(1-z_1\bar w_2)(1-z_2\bar w_1)}, \end{align} $$
$$ \begin{align} \tilde T^2(h)(z)&=\int_{\mathbb D^2}\frac{(\bar w_1-\bar w_2)^2h(w)dV}{\pi^2(1-z_1\bar w_1)^2(1-z_2\bar w_2)^2(1-z_1\bar w_2)(1-z_2\bar w_1)}, \end{align} $$
and
![]() $\|T^2_2\|_{L^p_{\text {anti}}(\mathbb D^2,|J_{\mathbb C}\Phi _2|^{2-p})}=\|\tilde T^2\|_{L^p_{\text {sym}}(\mathbb D^2,|J_{\mathbb C}\Phi _2|^{2})}$
provided one of the norms is finite. Thus it suffices to show that
$\|T^2_2\|_{L^p_{\text {anti}}(\mathbb D^2,|J_{\mathbb C}\Phi _2|^{2-p})}=\|\tilde T^2\|_{L^p_{\text {sym}}(\mathbb D^2,|J_{\mathbb C}\Phi _2|^{2})}$
provided one of the norms is finite. Thus it suffices to show that
![]() $\tilde T^2$
is unbounded on
$\tilde T^2$
is unbounded on
![]() $L^p_{\text {sym}}(\mathbb D^2,|J_{\mathbb C}\Phi _2|^{2})$
for
$L^p_{\text {sym}}(\mathbb D^2,|J_{\mathbb C}\Phi _2|^{2})$
for
![]() $p=4$
. For
$p=4$
. For
![]() $s\in [\frac {1}{2},1)$
, we set
$s\in [\frac {1}{2},1)$
, we set
Then
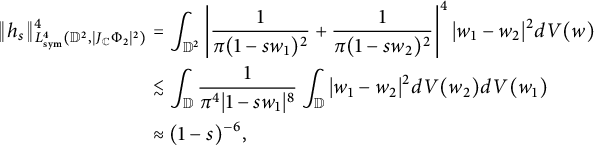 $$ \begin{align*} \|h_s\|^4_{L^4_{\text{sym}}(\mathbb D^2,|J_{\mathbb C}\Phi_2|^{2})}&=\int_{\mathbb D^2}\left|\frac{1}{\pi(1-sw_1)^2}+\frac{1}{\pi(1-sw_2)^2}\right|^4| w_1- w_2|^2dV(w)\\&\lesssim\int_{\mathbb D}\frac{1}{\pi^{4}|1-sw_1|^{8}}\int_{\mathbb D}| w_1- w_2|^{2}dV(w_2)dV(w_1) \\&\approx (1-s)^{-6}, \end{align*} $$
$$ \begin{align*} \|h_s\|^4_{L^4_{\text{sym}}(\mathbb D^2,|J_{\mathbb C}\Phi_2|^{2})}&=\int_{\mathbb D^2}\left|\frac{1}{\pi(1-sw_1)^2}+\frac{1}{\pi(1-sw_2)^2}\right|^4| w_1- w_2|^2dV(w)\\&\lesssim\int_{\mathbb D}\frac{1}{\pi^{4}|1-sw_1|^{8}}\int_{\mathbb D}| w_1- w_2|^{2}dV(w_2)dV(w_1) \\&\approx (1-s)^{-6}, \end{align*} $$
where the last equality follows from the Forelli–Rudin estimates (2.8). Note that the kernel function of
![]() $\tilde {T}^2$
is anti-holomorphic in w variables and
$\tilde {T}^2$
is anti-holomorphic in w variables and
![]() $h_s$
can be expressed in terms the conjugate of the Bergman kernels:
$h_s$
can be expressed in terms the conjugate of the Bergman kernels:
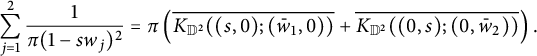 $$ \begin{align*} \sum_{j=1}^2\frac{1}{\pi(1-sw_j)^2}={\pi}\left(\overline{K_{\mathbb D^2}((s,0);(\bar w_1,0))}+\overline{K_{\mathbb D^2}((0,s);(0,\bar w_2))}\right). \end{align*} $$
$$ \begin{align*} \sum_{j=1}^2\frac{1}{\pi(1-sw_j)^2}={\pi}\left(\overline{K_{\mathbb D^2}((s,0);(\bar w_1,0))}+\overline{K_{\mathbb D^2}((0,s);(0,\bar w_2))}\right). \end{align*} $$
The reproducing property of the Bergman projection implies:
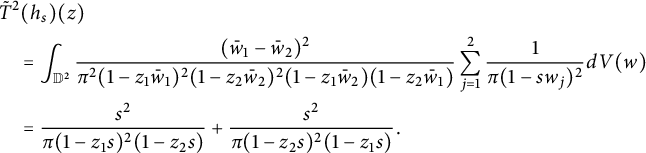 $$ \begin{align*} &\tilde T^2(h_s)(z)\\& \quad =\int_{\mathbb D^2}\frac{(\bar w_1-\bar w_2)^2}{\pi^2(1-z_1\bar w_1)^2(1-z_2\bar w_2)^2(1-z_1\bar w_2)(1-z_2\bar w_1)}\sum_{j=1}^2\frac{1}{\pi(1-sw_j)^2}dV(w)\\& \quad =\frac{s^2}{\pi(1-z_1s)^2(1-z_2s)}+\frac{s^2}{\pi(1-z_2s)^2(1-z_1s)}. \end{align*} $$
$$ \begin{align*} &\tilde T^2(h_s)(z)\\& \quad =\int_{\mathbb D^2}\frac{(\bar w_1-\bar w_2)^2}{\pi^2(1-z_1\bar w_1)^2(1-z_2\bar w_2)^2(1-z_1\bar w_2)(1-z_2\bar w_1)}\sum_{j=1}^2\frac{1}{\pi(1-sw_j)^2}dV(w)\\& \quad =\frac{s^2}{\pi(1-z_1s)^2(1-z_2s)}+\frac{s^2}{\pi(1-z_2s)^2(1-z_1s)}. \end{align*} $$
Thus
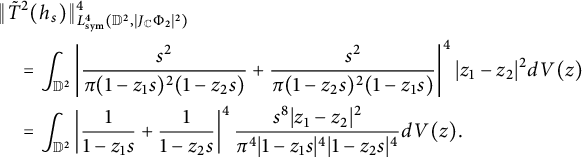 $$ \begin{align} &\|\tilde T^2(h_s)\|^4_{L^4_{\text{sym}}(\mathbb D^2,|J_{\mathbb C}\Phi_2|^{2})}\nonumber\\& \quad =\int_{\mathbb D^2}\left|\frac{s^2}{\pi(1-z_1s)^2(1-z_2s)}+\frac{s^2}{\pi(1-z_2s)^2(1-z_1s)}\right|^4|z_1-z_2|^2dV(z)\nonumber\\& \quad =\int_{\mathbb D^2}\left|\frac{1}{1-z_1s}+\frac{1}{1-z_2s}\right|^4\frac{s^8|z_1-z_2|^2}{\pi^4|1-z_1s|^4|1-z_2s|^4}dV(z). \end{align} $$
$$ \begin{align} &\|\tilde T^2(h_s)\|^4_{L^4_{\text{sym}}(\mathbb D^2,|J_{\mathbb C}\Phi_2|^{2})}\nonumber\\& \quad =\int_{\mathbb D^2}\left|\frac{s^2}{\pi(1-z_1s)^2(1-z_2s)}+\frac{s^2}{\pi(1-z_2s)^2(1-z_1s)}\right|^4|z_1-z_2|^2dV(z)\nonumber\\& \quad =\int_{\mathbb D^2}\left|\frac{1}{1-z_1s}+\frac{1}{1-z_2s}\right|^4\frac{s^8|z_1-z_2|^2}{\pi^4|1-z_1s|^4|1-z_2s|^4}dV(z). \end{align} $$
For fixed
![]() $s<1$
, set
$s<1$
, set
![]() $U(s)=\{z\in \mathbb D: \text {Arg}(1-zs)\in \left (-\frac {\pi }{6},\frac {\pi }{6}\right )\}$
. Then for
$U(s)=\{z\in \mathbb D: \text {Arg}(1-zs)\in \left (-\frac {\pi }{6},\frac {\pi }{6}\right )\}$
. Then for
![]() $z_1,z_2\in U(s)$
,
$z_1,z_2\in U(s)$
,
Applying this inequality to (4.4) gives
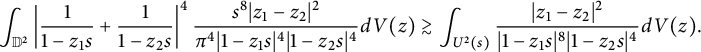 $$ \begin{align*} &\int_{\mathbb D^2}\left|\frac{1}{1-z_1s}+\frac{1}{1-z_2s}\right|^4\frac{s^8|z_1-z_2|^2}{\pi^4|1-z_1s|^4|1-z_2s|^4}dV(z)\gtrsim\int_{U^2(s)}\frac{|z_1-z_2|^2}{|1-z_1s|^8|1-z_2s|^4}dV(z).\end{align*} $$
$$ \begin{align*} &\int_{\mathbb D^2}\left|\frac{1}{1-z_1s}+\frac{1}{1-z_2s}\right|^4\frac{s^8|z_1-z_2|^2}{\pi^4|1-z_1s|^4|1-z_2s|^4}dV(z)\gtrsim\int_{U^2(s)}\frac{|z_1-z_2|^2}{|1-z_1s|^8|1-z_2s|^4}dV(z).\end{align*} $$
Since
we have
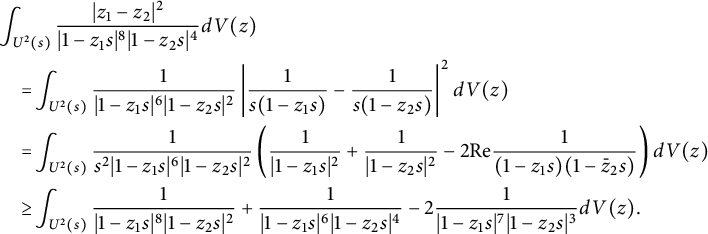 $$ \begin{align*}\kern-3pt &\int_{U^2(s)}\frac{|z_1-z_2|^2}{|1-z_1s|^8|1-z_2s|^4}dV(z)\\& \quad =\!\int_{U^2(s)}\frac{1}{|1-z_1s|^6|1-z_2s|^2}\left|\frac{1}{s(1-z_1s)}- \frac{1}{s(1-z_2s)}\right|^2dV(z) \\& \quad =\!\int_{U^2(s)}\frac{1}{s^2|1-z_1s|^6|1-z_2s|^2}\left(\frac{1}{|1-z_1s|^2}+\frac{1}{|1-z_2s|^2}-2\text{Re} \frac{1}{(1-z_1s)(1-\bar z_2 s)}\right)dV(z)\\& \quad \geq\! \int_{U^2(s)}\frac{1}{|1-z_1s|^8|1-z_2s|^2}+\frac{1}{|1-z_1s|^6|1-z_2s|^4}-2 \frac{1}{|1-z_1s|^7|1-z_2s|^3}dV(z). \end{align*} $$
$$ \begin{align*}\kern-3pt &\int_{U^2(s)}\frac{|z_1-z_2|^2}{|1-z_1s|^8|1-z_2s|^4}dV(z)\\& \quad =\!\int_{U^2(s)}\frac{1}{|1-z_1s|^6|1-z_2s|^2}\left|\frac{1}{s(1-z_1s)}- \frac{1}{s(1-z_2s)}\right|^2dV(z) \\& \quad =\!\int_{U^2(s)}\frac{1}{s^2|1-z_1s|^6|1-z_2s|^2}\left(\frac{1}{|1-z_1s|^2}+\frac{1}{|1-z_2s|^2}-2\text{Re} \frac{1}{(1-z_1s)(1-\bar z_2 s)}\right)dV(z)\\& \quad \geq\! \int_{U^2(s)}\frac{1}{|1-z_1s|^8|1-z_2s|^2}+\frac{1}{|1-z_1s|^6|1-z_2s|^4}-2 \frac{1}{|1-z_1s|^7|1-z_2s|^3}dV(z). \end{align*} $$
By realizing that
![]() $|1-zs|=s|\frac {1}{s}-z|$
and applying polar coordinates, one can obtain the following Forelli–Rudin estimates (2.8) on
$|1-zs|=s|\frac {1}{s}-z|$
and applying polar coordinates, one can obtain the following Forelli–Rudin estimates (2.8) on
![]() $U(s)$
.
$U(s)$
.
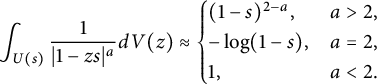 $$\begin{align*}\int_{U(s)}\frac{1}{|1-zs|^a}dV(z)\approx\begin{cases} (1-s)^{2-a},& a>2,\\ -\log(1-s),& a=2,\\ 1,&a<2. \end{cases}\end{align*}$$
$$\begin{align*}\int_{U(s)}\frac{1}{|1-zs|^a}dV(z)\approx\begin{cases} (1-s)^{2-a},& a>2,\\ -\log(1-s),& a=2,\\ 1,&a<2. \end{cases}\end{align*}$$
We leave the details of its proof to readers as an exercise. Using these estimates,
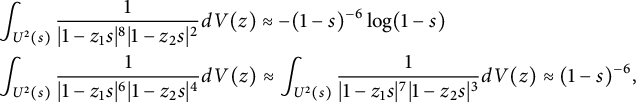 $$ \begin{align*} &\int_{U^2(s)}\frac{1}{|1-z_1s|^8|1-z_2s|^2}dV(z)\approx -(1-s)^{-6}\log(1-s)\\ &\int_{U^2(s)}\frac{1}{|1-z_1s|^6|1-z_2s|^4}dV(z)\approx \int_{U^2(s)} \frac{1}{|1-z_1s|^7|1-z_2s|^3}dV(z)\approx (1-s)^{-6}, \end{align*} $$
$$ \begin{align*} &\int_{U^2(s)}\frac{1}{|1-z_1s|^8|1-z_2s|^2}dV(z)\approx -(1-s)^{-6}\log(1-s)\\ &\int_{U^2(s)}\frac{1}{|1-z_1s|^6|1-z_2s|^4}dV(z)\approx \int_{U^2(s)} \frac{1}{|1-z_1s|^7|1-z_2s|^3}dV(z)\approx (1-s)^{-6}, \end{align*} $$
which implies that
![]() $\|\tilde T^2(h_s)\|^4_{L^4_{\text {sym}}(\mathbb D^2,|J_{\mathbb C}\Phi _2|^{2})}\approx -(1-s)^{-6}\log (1-s)$
.
$\|\tilde T^2(h_s)\|^4_{L^4_{\text {sym}}(\mathbb D^2,|J_{\mathbb C}\Phi _2|^{2})}\approx -(1-s)^{-6}\log (1-s)$
.
As
![]() $s\to 1$
,
$s\to 1$
,
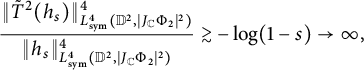 $$\begin{align*}\frac{\|\tilde T^2(h_s)\|^4_{L^4_{\text{sym}}(\mathbb D^2,|J_{\mathbb C}\Phi_2|^{2})}}{\| h_s\|^4_{L^4_{\text{sym}}(\mathbb D^2,|J_{\mathbb C}\Phi_2|^{2})}}\gtrsim-\log(1-s)\to \infty, \end{align*}$$
$$\begin{align*}\frac{\|\tilde T^2(h_s)\|^4_{L^4_{\text{sym}}(\mathbb D^2,|J_{\mathbb C}\Phi_2|^{2})}}{\| h_s\|^4_{L^4_{\text{sym}}(\mathbb D^2,|J_{\mathbb C}\Phi_2|^{2})}}\gtrsim-\log(1-s)\to \infty, \end{align*}$$
proving that
![]() $\tilde T^2$
is unbounded on
$\tilde T^2$
is unbounded on
![]() $L^4_{\text {sym}}(\mathbb D^2,|J_{\mathbb C}\Phi _2|^{2})$
.
$L^4_{\text {sym}}(\mathbb D^2,|J_{\mathbb C}\Phi _2|^{2})$
.
4.2 The case for general n
Like the case
![]() $n=2$
, our proof for general n also involves a decomposition of
$n=2$
, our proof for general n also involves a decomposition of
![]() $P_{\mathbb D^n}$
into operators
$P_{\mathbb D^n}$
into operators
![]() $T^n_1$
and
$T^n_1$
and
![]() $T^n_2$
.
$T^n_2$
.
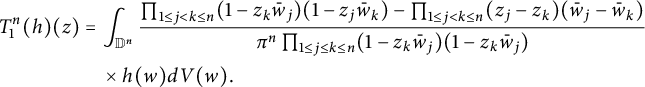 $$ \begin{align} T^n_{1}(h)(z)&=\int_{\mathbb D^n}\frac{\prod_{1\leq j<k\leq n}(1-z_k\bar w_j)(1-z_j\bar w_k)-\prod_{1\leq j<k\leq n}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{1\leq j\leq k\leq n}(1-z_k\bar w_j)(1-z_k\bar w_j)}\nonumber\\& \quad \times h(w)dV(w). \end{align} $$
$$ \begin{align} T^n_{1}(h)(z)&=\int_{\mathbb D^n}\frac{\prod_{1\leq j<k\leq n}(1-z_k\bar w_j)(1-z_j\bar w_k)-\prod_{1\leq j<k\leq n}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{1\leq j\leq k\leq n}(1-z_k\bar w_j)(1-z_k\bar w_j)}\nonumber\\& \quad \times h(w)dV(w). \end{align} $$
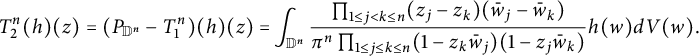 $$ \begin{align} T^n_{2}(h)(z)&=(P_{\mathbb D^n}-T^n_{1})(h)(z)=\!\int_{\mathbb D^n}\frac{\prod_{1\leq j<k\leq n}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{1\leq j\leq k\leq n}(1-z_k\bar w_j)(1-z_j\bar w_k)}h(w)dV(w).\nonumber\\ \end{align} $$
$$ \begin{align} T^n_{2}(h)(z)&=(P_{\mathbb D^n}-T^n_{1})(h)(z)=\!\int_{\mathbb D^n}\frac{\prod_{1\leq j<k\leq n}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{1\leq j\leq k\leq n}(1-z_k\bar w_j)(1-z_j\bar w_k)}h(w)dV(w).\nonumber\\ \end{align} $$
Lemma 4.3
![]() $T^n_1$
is a zero operator on
$T^n_1$
is a zero operator on
![]() $L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
.
$L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
.
Proof Recall that
![]() $\tau _{j,k}$
is the permutation that interchanges variables
$\tau _{j,k}$
is the permutation that interchanges variables
![]() $w_j$
and
$w_j$
and
![]() $w_k$
, and a kernel function
$w_k$
, and a kernel function
![]() $K(z;\bar w)$
on
$K(z;\bar w)$
on
![]() $\mathbb D^n\times \mathbb D^n$
is called
$\mathbb D^n\times \mathbb D^n$
is called
![]() $(j,k)$
-symmetric in w if
$(j,k)$
-symmetric in w if
![]() $K(z;\bar w)=K(z;\bar \tau _{j,k}(w))$
. If
$K(z;\bar w)=K(z;\bar \tau _{j,k}(w))$
. If
![]() $K(z;\bar w)$
is
$K(z;\bar w)$
is
![]() $(j,k)$
-symmetric in
$(j,k)$
-symmetric in
![]() $\bar w$
, then for any antisymmetric
$\bar w$
, then for any antisymmetric
![]() $f\in L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
, we have
$f\in L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
, we have
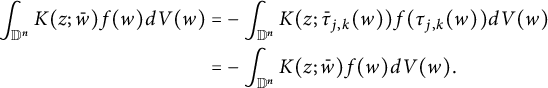 $$ \begin{align*} \int_{\mathbb D^n}K(z;\bar w)f(w)dV(w)&=-\int_{\mathbb D^n}K(z;\bar\tau_{j,k} (w))f(\tau_{j,k}(w))dV(w)\\&=-\int_{\mathbb D^n}K(z;\bar w)f(w)dV(w). \end{align*} $$
$$ \begin{align*} \int_{\mathbb D^n}K(z;\bar w)f(w)dV(w)&=-\int_{\mathbb D^n}K(z;\bar\tau_{j,k} (w))f(\tau_{j,k}(w))dV(w)\\&=-\int_{\mathbb D^n}K(z;\bar w)f(w)dV(w). \end{align*} $$
Thus operators with
![]() $(j,k)$
-symmetric kernel functions in w annihilate
$(j,k)$
-symmetric kernel functions in w annihilate
![]() $ L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
.
$ L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
.
For
![]() $l=1,\dots ,n$
, we define the operator
$l=1,\dots ,n$
, we define the operator
![]() $P_l$
to be as follows:
$P_l$
to be as follows:
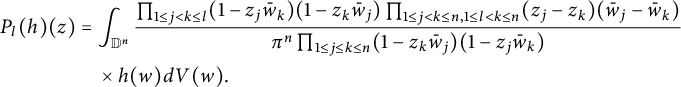 $$ \begin{align} P_{l}(h)(z)&=\int_{\mathbb D^n}\frac{\prod_{1\leq j<k\leq l}(1-z_j\bar w_k)(1-z_k\bar w_j)\prod_{1\leq j<k\leq n,1\leq l< k\leq n}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{1\leq j\leq k\leq n}(1-z_k\bar w_j)(1-z_j\bar w_k)}\nonumber\\& \quad \times h(w)dV(w). \end{align} $$
$$ \begin{align} P_{l}(h)(z)&=\int_{\mathbb D^n}\frac{\prod_{1\leq j<k\leq l}(1-z_j\bar w_k)(1-z_k\bar w_j)\prod_{1\leq j<k\leq n,1\leq l< k\leq n}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{1\leq j\leq k\leq n}(1-z_k\bar w_j)(1-z_j\bar w_k)}\nonumber\\& \quad \times h(w)dV(w). \end{align} $$
Then
![]() $P_1=T^n_2$
and
$P_1=T^n_2$
and
![]() $P_n=P_{\mathbb D^n}$
. We claim that
$P_n=P_{\mathbb D^n}$
. We claim that
![]() $P_{\mathbb D^n}=P_{l}$
on
$P_{\mathbb D^n}=P_{l}$
on
![]() $L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
for all
$L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
for all
![]() $l=1,\dots ,n$
. Then
$l=1,\dots ,n$
. Then
![]() $T^n_1=P_{\mathbb D^n}-P_1=0$
on
$T^n_1=P_{\mathbb D^n}-P_1=0$
on
![]() $L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
. We prove the claim by induction on l.
$L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
. We prove the claim by induction on l.
Let
![]() $K_l$
denote the kernel function of
$K_l$
denote the kernel function of
![]() $P_l$
. When
$P_l$
. When
![]() $l=2$
,
$l=2$
,
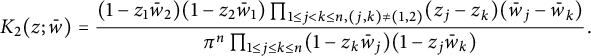 $$ \begin{align*} K_{2}(z;\bar w)&=\frac{(1-z_1\bar w_2)(1-z_2\bar w_1)\prod_{1\leq j<k\leq n,(j,k)\neq(1,2)}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{1\leq j\leq k\leq n}(1-z_k\bar w_j)(1-z_j\bar w_k)}. \end{align*} $$
$$ \begin{align*} K_{2}(z;\bar w)&=\frac{(1-z_1\bar w_2)(1-z_2\bar w_1)\prod_{1\leq j<k\leq n,(j,k)\neq(1,2)}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{1\leq j\leq k\leq n}(1-z_k\bar w_j)(1-z_j\bar w_k)}. \end{align*} $$
Then
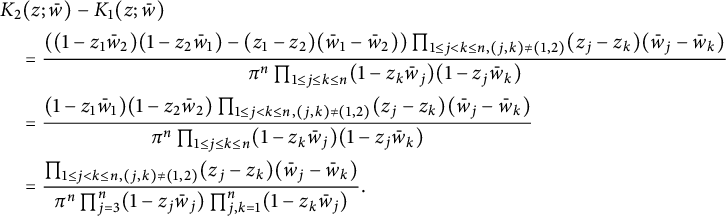 $$ \begin{align*}&K_{2}(z;\bar w)-K_{1}(z;\bar w)\\& \quad = \frac{((1-z_1\bar w_2)(1-z_2\bar w_1)-(z_1-z_2)(\bar w_1-\bar w_2))\prod_{1\leq j<k\leq n,(j,k)\neq(1,2)}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{1\leq j\leq k\leq n}(1-z_k\bar w_j)(1-z_j\bar w_k)}\\& \quad = \frac{(1-z_1\bar w_1)(1-z_2\bar w_2)\prod_{1\leq j<k\leq n,(j,k)\neq(1,2)}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{1\leq j\leq k\leq n}(1-z_k\bar w_j)(1-z_j\bar w_k)}\\& \quad = \frac{\prod_{1\leq j<k\leq n,(j,k)\neq(1,2)}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{j=3}^n(1-z_j\bar w_j)\prod_{j,k=1}^n(1-z_k\bar w_j)}. \end{align*} $$
$$ \begin{align*}&K_{2}(z;\bar w)-K_{1}(z;\bar w)\\& \quad = \frac{((1-z_1\bar w_2)(1-z_2\bar w_1)-(z_1-z_2)(\bar w_1-\bar w_2))\prod_{1\leq j<k\leq n,(j,k)\neq(1,2)}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{1\leq j\leq k\leq n}(1-z_k\bar w_j)(1-z_j\bar w_k)}\\& \quad = \frac{(1-z_1\bar w_1)(1-z_2\bar w_2)\prod_{1\leq j<k\leq n,(j,k)\neq(1,2)}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{1\leq j\leq k\leq n}(1-z_k\bar w_j)(1-z_j\bar w_k)}\\& \quad = \frac{\prod_{1\leq j<k\leq n,(j,k)\neq(1,2)}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{j=3}^n(1-z_j\bar w_j)\prod_{j,k=1}^n(1-z_k\bar w_j)}. \end{align*} $$
It is not hard to check that
![]() $K_{2}-K_{1}$
is
$K_{2}-K_{1}$
is
![]() $(1,2)$
-symmetric in w which shows that
$(1,2)$
-symmetric in w which shows that
![]() $P_{1}=P_2$
on
$P_{1}=P_2$
on
![]() $L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
.
$L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
.
Suppose that
![]() $P_{1}=P_l$
on
$P_{1}=P_l$
on
![]() $L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
for
$L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
for
![]() $l=m$
. We show that
$l=m$
. We show that
![]() $P_{m+1}=P_m$
on
$P_{m+1}=P_m$
on
![]() $L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
. Let
$L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
. Let
![]() $\mathcal R_m$
denote the power set
$\mathcal R_m$
denote the power set
Given
![]() $\mathcal I\in \mathcal R_m$
, let
$\mathcal I\in \mathcal R_m$
, let
![]() $|\mathcal I|$
denote the cardinality of
$|\mathcal I|$
denote the cardinality of
![]() $\mathcal I$
. For simplicity of notation, we set
$\mathcal I$
. For simplicity of notation, we set
![]() $a_{j,k}=1-z_j\bar w_k$
and
$a_{j,k}=1-z_j\bar w_k$
and
![]() $b_{j,k}=(z_j-z_k)(\bar w_j-\bar w_k)$
. Then for
$b_{j,k}=(z_j-z_k)(\bar w_j-\bar w_k)$
. Then for
![]() $j\neq k$
,
$j\neq k$
,
![]() $a_{j,k}a_{k,j}=a_{j,j}a_{kk}+b_{j,k}.$
Note that
$a_{j,k}a_{k,j}=a_{j,j}a_{kk}+b_{j,k}.$
Note that
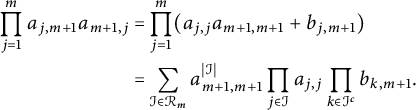 $$ \begin{align*} \prod_{j=1}^{m}a_{j,m+1} a_{m+1,j}=& \prod_{j=1}^{m}(a_{j,j} a_{m+1,m+1}+b_{j,m+1})\\ =& \sum_{\mathcal I\in \mathcal R_m}a_{m+1,m+1}^{|\mathcal I|}\prod_{j\in\mathcal I}a_{j,j} \prod_{k\in \mathcal I^c}b_{k,m+1}. \end{align*} $$
$$ \begin{align*} \prod_{j=1}^{m}a_{j,m+1} a_{m+1,j}=& \prod_{j=1}^{m}(a_{j,j} a_{m+1,m+1}+b_{j,m+1})\\ =& \sum_{\mathcal I\in \mathcal R_m}a_{m+1,m+1}^{|\mathcal I|}\prod_{j\in\mathcal I}a_{j,j} \prod_{k\in \mathcal I^c}b_{k,m+1}. \end{align*} $$
We set
Then
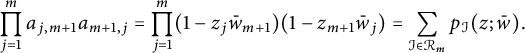 $$ \begin{align*}\prod_{j=1}^{m}a_{j,m+1}a_{m+1,j}=\prod_{j=1}^{m}(1-z_j\bar w_{m+1})(1-z_{m+1}\bar w_j)=\sum_{\mathcal I\in \mathcal R_m}p_{\mathcal I}(z;\bar w).\end{align*} $$
$$ \begin{align*}\prod_{j=1}^{m}a_{j,m+1}a_{m+1,j}=\prod_{j=1}^{m}(1-z_j\bar w_{m+1})(1-z_{m+1}\bar w_j)=\sum_{\mathcal I\in \mathcal R_m}p_{\mathcal I}(z;\bar w).\end{align*} $$
Let
![]() $K_m$
and
$K_m$
and
![]() $K_{m+1}$
be the kernel function of
$K_{m+1}$
be the kernel function of
![]() $P_m$
and
$P_m$
and
![]() $P_{m+1}$
, respectively, as in (4.7). Let
$P_{m+1}$
, respectively, as in (4.7). Let
![]() $K_{m,\mathcal I}$
denote the kernel function
$K_{m,\mathcal I}$
denote the kernel function
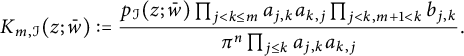 $$\begin{align*}K_{m,\mathcal I}(z;\bar w):=\frac{p_{\mathcal I}(z;\bar w)\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}. \end{align*}$$
$$\begin{align*}K_{m,\mathcal I}(z;\bar w):=\frac{p_{\mathcal I}(z;\bar w)\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}. \end{align*}$$
We can express
![]() $K_m$
and
$K_m$
and
![]() $K_{m+1}$
in terms of
$K_{m+1}$
in terms of
![]() $K_{m,\mathcal I}(z;\bar w)$
:
$K_{m,\mathcal I}(z;\bar w)$
:
 $$ \begin{align*} K_m(z;\bar w)&=\frac{\prod_{j<k\leq m}(1-z_j\bar w_k)(1-z_k\bar w_j)\prod_{j<k, m<k}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{j\leq k}(1-z_k\bar w_j)(1-z_j\bar w_k)}\\ &=\frac{p_{\emptyset}(z;\bar w)\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k, m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}\\ &=K_{m,\emptyset}(z;\bar w), \end{align*} $$
$$ \begin{align*} K_m(z;\bar w)&=\frac{\prod_{j<k\leq m}(1-z_j\bar w_k)(1-z_k\bar w_j)\prod_{j<k, m<k}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{j\leq k}(1-z_k\bar w_j)(1-z_j\bar w_k)}\\ &=\frac{p_{\emptyset}(z;\bar w)\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k, m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}\\ &=K_{m,\emptyset}(z;\bar w), \end{align*} $$
and
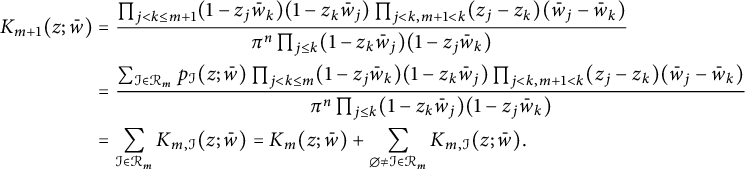 $$ \begin{align*} K_{m+1}(z;\bar w)&=\frac{\prod_{j<k\leq m+1}(1-z_j\bar w_k)(1-z_k\bar w_j)\prod_{j<k,m+1<k}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{j\leq k}(1-z_k\bar w_j)(1-z_j\bar w_k)}\\&=\frac{\sum_{\mathcal I\in \mathcal R_m}p_{\mathcal I}(z;\bar w)\prod_{j<k\leq m}(1-z_j\bar w_k)(1-z_k\bar w_j)\prod_{j<k,m+1<k}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{j\leq k}(1-z_k\bar w_j)(1-z_j\bar w_k)}\\&=\sum_{\mathcal I\in \mathcal R_m}K_{m,\mathcal I}(z;\bar w)=K_{m}(z;\bar w)+\sum_{\emptyset\neq\mathcal I\in \mathcal R_m}K_{m,\mathcal I}(z;\bar w). \end{align*} $$
$$ \begin{align*} K_{m+1}(z;\bar w)&=\frac{\prod_{j<k\leq m+1}(1-z_j\bar w_k)(1-z_k\bar w_j)\prod_{j<k,m+1<k}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{j\leq k}(1-z_k\bar w_j)(1-z_j\bar w_k)}\\&=\frac{\sum_{\mathcal I\in \mathcal R_m}p_{\mathcal I}(z;\bar w)\prod_{j<k\leq m}(1-z_j\bar w_k)(1-z_k\bar w_j)\prod_{j<k,m+1<k}(z_j-z_k)(\bar w_j-\bar w_k)}{\pi^n\prod_{j\leq k}(1-z_k\bar w_j)(1-z_j\bar w_k)}\\&=\sum_{\mathcal I\in \mathcal R_m}K_{m,\mathcal I}(z;\bar w)=K_{m}(z;\bar w)+\sum_{\emptyset\neq\mathcal I\in \mathcal R_m}K_{m,\mathcal I}(z;\bar w). \end{align*} $$
We show that for any nonempty
![]() $\mathcal I\in \mathcal R_m$
,
$\mathcal I\in \mathcal R_m$
,
![]() $K_{m,\mathcal I}$
is a linear combination of
$K_{m,\mathcal I}$
is a linear combination of
![]() $(j,k)$
-symmetric kernel functions. Then for antisymmetric
$(j,k)$
-symmetric kernel functions. Then for antisymmetric
![]() $f\in L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
,
$f\in L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
,
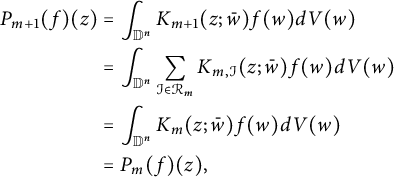 $$ \begin{align*} P_{m+1}(f)(z)&=\int_{\mathbb D^n}K_{m+1}(z;\bar w)f(w)dV(w)\\&=\int_{\mathbb D^n}\sum_{\mathcal I\in\mathcal R_m}K_{m,\mathcal I}(z;\bar w)f(w)dV(w)\\ &=\int_{\mathbb D^n}K_{m}(z;\bar w)f(w)dV(w)\\ &=P_{m}(f)(z), \end{align*} $$
$$ \begin{align*} P_{m+1}(f)(z)&=\int_{\mathbb D^n}K_{m+1}(z;\bar w)f(w)dV(w)\\&=\int_{\mathbb D^n}\sum_{\mathcal I\in\mathcal R_m}K_{m,\mathcal I}(z;\bar w)f(w)dV(w)\\ &=\int_{\mathbb D^n}K_{m}(z;\bar w)f(w)dV(w)\\ &=P_{m}(f)(z), \end{align*} $$
which completes the induction and the proof of the lemma. When
![]() $|\mathcal I|>1$
, there exists
$|\mathcal I|>1$
, there exists
![]() $j_1,j_2\in \mathcal I$
, and
$j_1,j_2\in \mathcal I$
, and
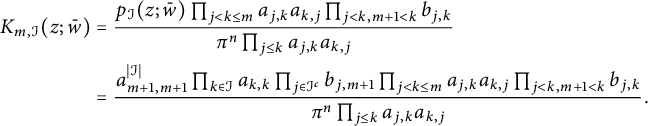 $$ \begin{align*} K_{m,\mathcal I}(z;\bar w)&=\frac{p_{\mathcal I}(z;\bar w)\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}\\ &=\frac{a_{m+1,m+1}^{|\mathcal I|}\prod_{k\in\mathcal I}a_{k,k} \prod_{j\in \mathcal I^c}b_{j,m+1}\prod_{ j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}. \end{align*} $$
$$ \begin{align*} K_{m,\mathcal I}(z;\bar w)&=\frac{p_{\mathcal I}(z;\bar w)\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}\\ &=\frac{a_{m+1,m+1}^{|\mathcal I|}\prod_{k\in\mathcal I}a_{k,k} \prod_{j\in \mathcal I^c}b_{j,m+1}\prod_{ j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}. \end{align*} $$
It’s easy to see that
![]() $K_{m,\mathcal I}(z;\bar w)$
is
$K_{m,\mathcal I}(z;\bar w)$
is
![]() $(j_1,j_2)$
-symmetric.
$(j_1,j_2)$
-symmetric.
Now we turn to consider the case when
![]() $\mathcal I=\{j_0\}$
. Without loss of generality, we let
$\mathcal I=\{j_0\}$
. Without loss of generality, we let
![]() $j_0=1$
.
$j_0=1$
.
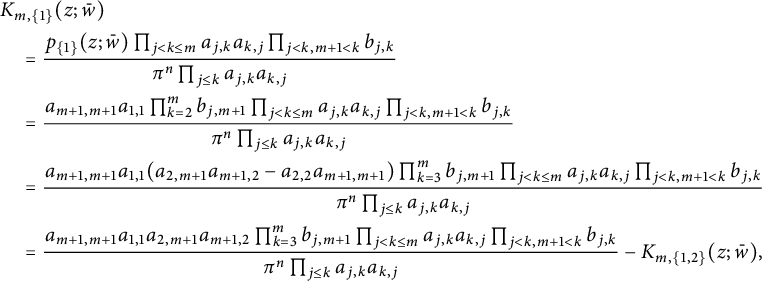 $$ \begin{align*}&K_{m,\{1\}}(z;\bar w)\\& \quad =\frac{p_{\{1\}}(z;\bar w)\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}\\& \quad =\frac{a_{m+1,m+1}a_{1,1} \prod_{k=2}^mb_{j,m+1}\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}\\& \quad =\frac{a_{m+1,m+1}a_{1,1} (a_{2,m+1}a_{m+1,2}-a_{2,2}a_{m+1,m+1})\prod_{k=3}^mb_{j,m+1}\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}} \\& \quad =\frac{a_{m+1,m+1}a_{1,1} a_{2,m+1}a_{m+1,2}\prod_{k=3}^mb_{j,m+1}\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}-K_{m,\{1,2\}}(z;\bar w), \end{align*} $$
$$ \begin{align*}&K_{m,\{1\}}(z;\bar w)\\& \quad =\frac{p_{\{1\}}(z;\bar w)\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}\\& \quad =\frac{a_{m+1,m+1}a_{1,1} \prod_{k=2}^mb_{j,m+1}\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}\\& \quad =\frac{a_{m+1,m+1}a_{1,1} (a_{2,m+1}a_{m+1,2}-a_{2,2}a_{m+1,m+1})\prod_{k=3}^mb_{j,m+1}\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}} \\& \quad =\frac{a_{m+1,m+1}a_{1,1} a_{2,m+1}a_{m+1,2}\prod_{k=3}^mb_{j,m+1}\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}-K_{m,\{1,2\}}(z;\bar w), \end{align*} $$
where
![]() $K_{m,\{1,2\}}(z;\bar w)$
is
$K_{m,\{1,2\}}(z;\bar w)$
is
![]() $(1,2)$
-symmetric in w.
$(1,2)$
-symmetric in w.
Since
![]() $b_{3,m+1}=a_{3,m+1}a_{m+1,3}-a_{3,3}a_{m+1,m+1}$
, we have
$b_{3,m+1}=a_{3,m+1}a_{m+1,3}-a_{3,3}a_{m+1,m+1}$
, we have
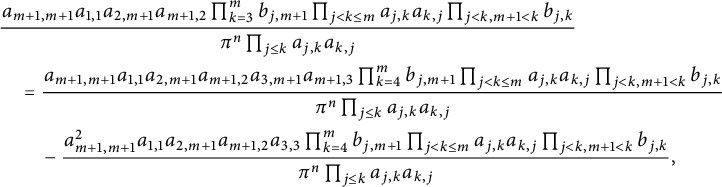 $$ \begin{align*} &\frac{a_{m+1,m+1}a_{1,1} a_{2,m+1}a_{m+1,2}\prod_{k=3}^mb_{j,m+1}\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}\\& \quad =\frac{a_{m+1,m+1}a_{1,1} a_{2,m+1}a_{m+1,2}a_{3,m+1}a_{m+1,3}\prod_{k=4}^mb_{j,m+1}\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}\\& \qquad -\frac{a^2_{m+1,m+1}a_{1,1} a_{2,m+1}a_{m+1,2}a_{3,3}\prod_{k=4}^mb_{j,m+1}\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}, \end{align*} $$
$$ \begin{align*} &\frac{a_{m+1,m+1}a_{1,1} a_{2,m+1}a_{m+1,2}\prod_{k=3}^mb_{j,m+1}\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}\\& \quad =\frac{a_{m+1,m+1}a_{1,1} a_{2,m+1}a_{m+1,2}a_{3,m+1}a_{m+1,3}\prod_{k=4}^mb_{j,m+1}\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}\\& \qquad -\frac{a^2_{m+1,m+1}a_{1,1} a_{2,m+1}a_{m+1,2}a_{3,3}\prod_{k=4}^mb_{j,m+1}\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}}, \end{align*} $$
where the negative term above is
![]() $(1,3)$
-symmetric in w. Repeating the above process using the identity
$(1,3)$
-symmetric in w. Repeating the above process using the identity
![]() $b_{j,m+1}=a_{j,m+1}a_{m+1,j}-a_{j,j}a_{m+1,m+1}$
until no
$b_{j,m+1}=a_{j,m+1}a_{m+1,j}-a_{j,j}a_{m+1,m+1}$
until no
![]() $b_{j,m+1}$
term left, we obtain
$b_{j,m+1}$
term left, we obtain
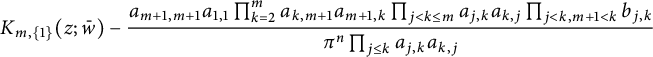 $$ \begin{align*} K_{m,\{1\}}(z;\bar w)-\frac{a_{m+1,m+1}a_{1,1}\prod_{k=2}^m a_{k,m+1}a_{m+1,k}\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}} \end{align*} $$
$$ \begin{align*} K_{m,\{1\}}(z;\bar w)-\frac{a_{m+1,m+1}a_{1,1}\prod_{k=2}^m a_{k,m+1}a_{m+1,k}\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}} \end{align*} $$
is a linear combination of functions that are
![]() $(1,j)$
-symmetric in w. Since the function
$(1,j)$
-symmetric in w. Since the function
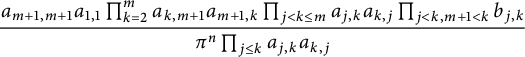 $$\begin{align*}\frac{a_{m+1,m+1}a_{1,1}\prod_{k=2}^m a_{k,m+1}a_{m+1,k}\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}} \end{align*}$$
$$\begin{align*}\frac{a_{m+1,m+1}a_{1,1}\prod_{k=2}^m a_{k,m+1}a_{m+1,k}\prod_{j<k\leq m}a_{j,k}a_{k,j}\prod_{j<k,m+1<k}b_{j,k}}{\pi^n\prod_{j\leq k}a_{j,k}a_{k,j}} \end{align*}$$
is
![]() $(1,m+1)$
-symmetric in w, we are done.
$(1,m+1)$
-symmetric in w, we are done.
Since
![]() $T^n_2=P_{\mathbb D^n}$
on
$T^n_2=P_{\mathbb D^n}$
on
![]() $L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p}|)$
, the next theorem implies Theorem 2.4 for general n.
$L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p}|)$
, the next theorem implies Theorem 2.4 for general n.
Theorem 4.4
![]() $T^n_2$
is unbounded on
$T^n_2$
is unbounded on
![]() $L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
for
$L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
for
![]() $p=\frac {2n}{n-1}$
.
$p=\frac {2n}{n-1}$
.
Proof The proof for the case
![]() $n>2$
follows from a similar argument as in the proof of Theorem 4.2. Let
$n>2$
follows from a similar argument as in the proof of Theorem 4.2. Let
![]() $\tilde T^n$
denote the operator given as follows:
$\tilde T^n$
denote the operator given as follows:
Then
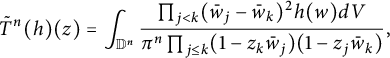 $$ \begin{align} \tilde T^n(h)(z)&=\int_{\mathbb D^n}\frac{\prod_{j<k}(\bar w_j-\bar w_k)^2h(w)dV}{\pi^n\prod_{j\leq k}(1-z_k\bar w_j)(1-z_j\bar w_k)}, \end{align} $$
$$ \begin{align} \tilde T^n(h)(z)&=\int_{\mathbb D^n}\frac{\prod_{j<k}(\bar w_j-\bar w_k)^2h(w)dV}{\pi^n\prod_{j\leq k}(1-z_k\bar w_j)(1-z_j\bar w_k)}, \end{align} $$
and
![]() $\|T^n_2\|_{L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})}=\|\tilde T^n\|_{L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2})}$
provided one of the norms is finite. Thus it suffices to show that
$\|T^n_2\|_{L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})}=\|\tilde T^n\|_{L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2})}$
provided one of the norms is finite. Thus it suffices to show that
![]() $\tilde T^n$
is unbounded on
$\tilde T^n$
is unbounded on
![]() $L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2})$
for
$L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2})$
for
![]() $p=\frac {2n}{n-1}$
.
$p=\frac {2n}{n-1}$
.
Recall that
![]() $\mathcal S_n$
is the set of all permutations of
$\mathcal S_n$
is the set of all permutations of
![]() $\{z_1,\dots ,z_n\}$
. For
$\{z_1,\dots ,z_n\}$
. For
![]() $s\in (0,1)$
, we set
$s\in (0,1)$
, we set
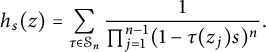 $$ \begin{align*}h_s(z)=\sum_{\tau\in \mathcal S_n}\frac{1}{\prod_{j=1}^{n-1}(1-\tau(z_j)s)^n}.\end{align*} $$
$$ \begin{align*}h_s(z)=\sum_{\tau\in \mathcal S_n}\frac{1}{\prod_{j=1}^{n-1}(1-\tau(z_j)s)^n}.\end{align*} $$
Then
![]() $h_s$
is a symmetric function with
$h_s$
is a symmetric function with
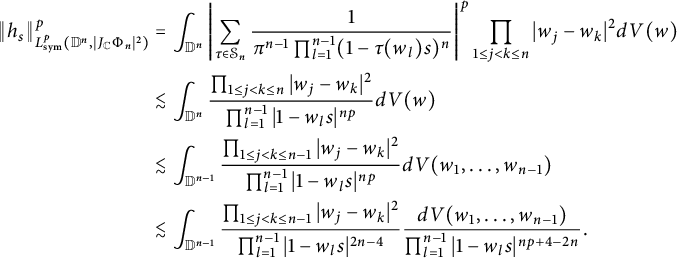 $$ \begin{align} \|h_s\|^p_{L^p_{\text{sym}}(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2})}\nonumber&=\int_{\mathbb D^n}\left|\sum_{\tau\in \mathcal S_n}\frac{1}{\pi^{n-1}\prod_{l=1}^{n-1}(1-\tau(w_l)s)^n}\right|^p\prod_{1\leq j<k\leq n }| w_j- w_k|^2dV(w)\nonumber\\ &\lesssim\int_{\mathbb D^n}\frac{\prod_{1\leq j<k\leq n}| w_j- w_k|^2}{\prod_{l=1}^{n-1}|1-w_ls|^{np}}dV(w)\nonumber\\ &\lesssim\int_{\mathbb D^{n-1}}\frac{\prod_{1\leq j<k\leq n-1}| w_j- w_k|^2}{\prod_{l=1}^{n-1}|1-w_ls|^{np}}dV(w_1,\dots,w_{n-1})\nonumber\\ &\lesssim\int_{\mathbb D^{n-1}}\frac{\prod_{1\leq j<k\leq n-1}| w_j- w_k|^2}{\prod_{l=1}^{n-1}|1-w_ls|^{2n-4}}\frac{dV(w_1,\dots,w_{n-1})}{\prod_{l=1}^{n-1}|1-w_ls|^{np+4-2n}}. \end{align} $$
$$ \begin{align} \|h_s\|^p_{L^p_{\text{sym}}(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2})}\nonumber&=\int_{\mathbb D^n}\left|\sum_{\tau\in \mathcal S_n}\frac{1}{\pi^{n-1}\prod_{l=1}^{n-1}(1-\tau(w_l)s)^n}\right|^p\prod_{1\leq j<k\leq n }| w_j- w_k|^2dV(w)\nonumber\\ &\lesssim\int_{\mathbb D^n}\frac{\prod_{1\leq j<k\leq n}| w_j- w_k|^2}{\prod_{l=1}^{n-1}|1-w_ls|^{np}}dV(w)\nonumber\\ &\lesssim\int_{\mathbb D^{n-1}}\frac{\prod_{1\leq j<k\leq n-1}| w_j- w_k|^2}{\prod_{l=1}^{n-1}|1-w_ls|^{np}}dV(w_1,\dots,w_{n-1})\nonumber\\ &\lesssim\int_{\mathbb D^{n-1}}\frac{\prod_{1\leq j<k\leq n-1}| w_j- w_k|^2}{\prod_{l=1}^{n-1}|1-w_ls|^{2n-4}}\frac{dV(w_1,\dots,w_{n-1})}{\prod_{l=1}^{n-1}|1-w_ls|^{np+4-2n}}. \end{align} $$
To evaluate the integral above, we need an
![]() $(n-2)$
-step procedure to eliminate the numerator of the integrand, i.e., we rewrite
$(n-2)$
-step procedure to eliminate the numerator of the integrand, i.e., we rewrite
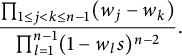 $$\begin{align*}\frac{\prod_{1\leq j<k\leq n-1}(w_j- w_k)}{\prod_{l=1}^{n-1}(1-w_ls)^{n-2}}.\end{align*}$$
$$\begin{align*}\frac{\prod_{1\leq j<k\leq n-1}(w_j- w_k)}{\prod_{l=1}^{n-1}(1-w_ls)^{n-2}}.\end{align*}$$
Step 1. Recall that by partial fractions:
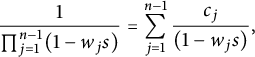 $$ \begin{align*}\frac{1}{\prod_{j=1}^{n-1}(1-w_js)}=\sum_{j=1}^{n-1}\frac{c_j}{(1-w_js)},\end{align*} $$
$$ \begin{align*}\frac{1}{\prod_{j=1}^{n-1}(1-w_js)}=\sum_{j=1}^{n-1}\frac{c_j}{(1-w_js)},\end{align*} $$
where
![]() $c_j=\frac {1}{s^{n-2}\prod _{k=1,k\neq j}^{n-1}({w_j}-{w_k})}$
. Then
$c_j=\frac {1}{s^{n-2}\prod _{k=1,k\neq j}^{n-1}({w_j}-{w_k})}$
. Then
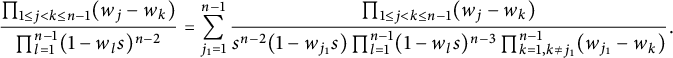 $$ \begin{align*}\frac{\prod_{1\leq j<k\leq n-1}(w_j- w_k)}{\prod_{l=1}^{n-1}(1-w_ls)^{n-2}}&=\sum_{j_1=1}^{n-1}\frac{\prod_{1\leq j< k\leq n-1}(w_j- w_k)}{s^{n-2}(1-{w}_{j_1}s)\prod_{l=1}^{n-1}(1-w_ls)^{n-3}\prod_{k=1,k\neq j_1}^{n-1}({w_{j_1}}-{w_k})}. \end{align*} $$
$$ \begin{align*}\frac{\prod_{1\leq j<k\leq n-1}(w_j- w_k)}{\prod_{l=1}^{n-1}(1-w_ls)^{n-2}}&=\sum_{j_1=1}^{n-1}\frac{\prod_{1\leq j< k\leq n-1}(w_j- w_k)}{s^{n-2}(1-{w}_{j_1}s)\prod_{l=1}^{n-1}(1-w_ls)^{n-3}\prod_{k=1,k\neq j_1}^{n-1}({w_{j_1}}-{w_k})}. \end{align*} $$
Step 2. Now we focus on the
![]() $j_1$
th term in the sum above:
$j_1$
th term in the sum above:
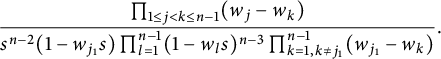 $$ \begin{align*}\frac{\prod_{1\leq j< k\leq n-1}(w_j- w_k)}{s^{n-2}(1-{w}_{j_1}s)\prod_{l=1}^{n-1}(1-w_ls)^{n-3}\prod_{k=1,k\neq j_1}^{n-1}({w_{j_1}}-{w_k})}.\end{align*} $$
$$ \begin{align*}\frac{\prod_{1\leq j< k\leq n-1}(w_j- w_k)}{s^{n-2}(1-{w}_{j_1}s)\prod_{l=1}^{n-1}(1-w_ls)^{n-3}\prod_{k=1,k\neq j_1}^{n-1}({w_{j_1}}-{w_k})}.\end{align*} $$
Applying the partial fractions yields
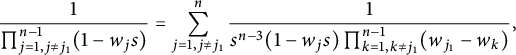 $$ \begin{align*}\frac{1}{\prod_{j=1,j\neq j_1}^{n-1}(1-w_js)}=\sum_{j=1,j\neq j_1}^{n}\frac{1}{s^{n-3}(1- w_js)\prod_{k=1,k\neq j_1}^{n-1}(w_{j_1}-w_{k})},\end{align*} $$
$$ \begin{align*}\frac{1}{\prod_{j=1,j\neq j_1}^{n-1}(1-w_js)}=\sum_{j=1,j\neq j_1}^{n}\frac{1}{s^{n-3}(1- w_js)\prod_{k=1,k\neq j_1}^{n-1}(w_{j_1}-w_{k})},\end{align*} $$
and
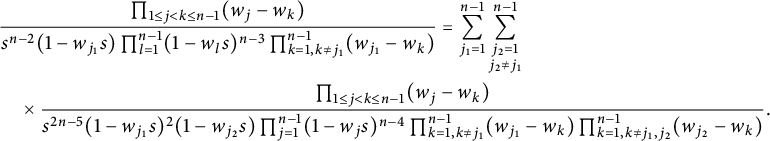 $$ \begin{align*} &\frac{\prod_{1\leq j< k\leq n-1}(w_j- w_k)}{s^{n-2}(1-{w}_{j_1}s)\prod_{l=1}^{n-1}(1-w_ls)^{n-3}\prod_{{k=1,k\neq j_1}}^{n-1}({w_{j_1}}-{w_k})}=\sum_{j_1=1}^{n-1}\sum_{\substack{j_2=1\\j_2\neq j_1}}^{n-1}\\& \quad \times \frac{\prod_{1\leq j<k\leq n-1}( w_j-w_k)}{s^{2n-5}(1-{w}_{j_1}s)^2(1-{w}_{j_2}s)\prod_{j=1}^{n-1}(1-w_js)^{n-4}\prod_{{k=1,k\neq j_1}}^{n-1}({w_{j_1}}-{w_k})\prod_{{k=1,k\neq j_1,j_2}}^{n-1}({w_{j_2}}-{w_k})}. \end{align*} $$
$$ \begin{align*} &\frac{\prod_{1\leq j< k\leq n-1}(w_j- w_k)}{s^{n-2}(1-{w}_{j_1}s)\prod_{l=1}^{n-1}(1-w_ls)^{n-3}\prod_{{k=1,k\neq j_1}}^{n-1}({w_{j_1}}-{w_k})}=\sum_{j_1=1}^{n-1}\sum_{\substack{j_2=1\\j_2\neq j_1}}^{n-1}\\& \quad \times \frac{\prod_{1\leq j<k\leq n-1}( w_j-w_k)}{s^{2n-5}(1-{w}_{j_1}s)^2(1-{w}_{j_2}s)\prod_{j=1}^{n-1}(1-w_js)^{n-4}\prod_{{k=1,k\neq j_1}}^{n-1}({w_{j_1}}-{w_k})\prod_{{k=1,k\neq j_1,j_2}}^{n-1}({w_{j_2}}-{w_k})}. \end{align*} $$
Step 3. As in Step 2, we turn to the term with sub-indices
![]() $(j_1,j_2)$
in the sum above and continue the process by doing partial fractions to
$(j_1,j_2)$
in the sum above and continue the process by doing partial fractions to
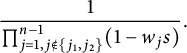 $$ \begin{align*}\frac{1}{\prod_{j=1,j\notin \{j_1,j_2\}}^{n-1}(1- w_js)}.\end{align*} $$
$$ \begin{align*}\frac{1}{\prod_{j=1,j\notin \{j_1,j_2\}}^{n-1}(1- w_js)}.\end{align*} $$
Repeat this process. Then after
![]() $n-2$
steps, we obtain
$n-2$
steps, we obtain
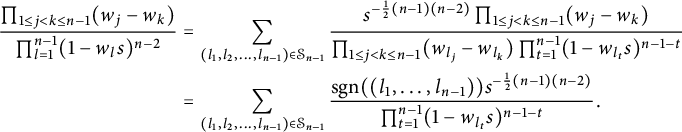 $$ \begin{align} \frac{\prod_{1\leq j<k\leq n-1}(w_j- w_k)}{\prod_{l=1}^{n-1}(1-w_ls)^{n-2}}\nonumber&=\sum_{(l_1, l_2,\dots,l_{n-1})\in \mathcal S_{n-1}}\frac{s^{-\frac{1}{2}(n-1)(n-2)}\prod_{1\leq j<k\leq n-1}(w_j- w_k)}{\prod_{1\leq j<k\leq n-1}(w_{l_j}- w_{l_k})\prod_{t=1}^{n-1}(1- w_{l_t}s)^{n-1-t}}\nonumber\\&=\sum_{(l_1, l_2,\dots,l_{n-1})\in \mathcal S_{n-1}}\frac{\text{sgn}((l_1,\dots,l_{n-1}))s^{-\frac{1}{2}(n-1)(n-2)}}{\prod_{t=1}^{n-1}(1- w_{l_t}s)^{n-1-t}}. \end{align} $$
$$ \begin{align} \frac{\prod_{1\leq j<k\leq n-1}(w_j- w_k)}{\prod_{l=1}^{n-1}(1-w_ls)^{n-2}}\nonumber&=\sum_{(l_1, l_2,\dots,l_{n-1})\in \mathcal S_{n-1}}\frac{s^{-\frac{1}{2}(n-1)(n-2)}\prod_{1\leq j<k\leq n-1}(w_j- w_k)}{\prod_{1\leq j<k\leq n-1}(w_{l_j}- w_{l_k})\prod_{t=1}^{n-1}(1- w_{l_t}s)^{n-1-t}}\nonumber\\&=\sum_{(l_1, l_2,\dots,l_{n-1})\in \mathcal S_{n-1}}\frac{\text{sgn}((l_1,\dots,l_{n-1}))s^{-\frac{1}{2}(n-1)(n-2)}}{\prod_{t=1}^{n-1}(1- w_{l_t}s)^{n-1-t}}. \end{align} $$
Here,
![]() $\text {sgn}((l_1,\dots ,l_{n-1}))$
is the sign of the permutation
$\text {sgn}((l_1,\dots ,l_{n-1}))$
is the sign of the permutation
![]() $(l_1,\dots ,l_{n-1})$
.
$(l_1,\dots ,l_{n-1})$
.
Applying this identity to (4.9) and using the triangle inequality, we obtain
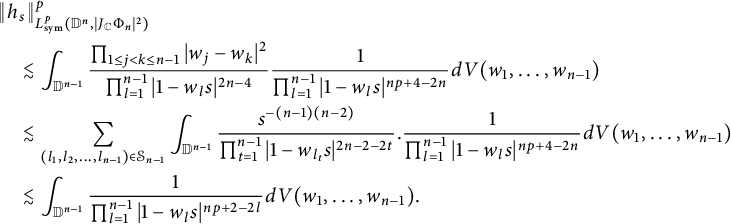 $$ \begin{align} &\|h_s\|^p_{L^p_{\text{sym}}(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2})}\nonumber\\& \quad \lesssim\int_{\mathbb D^{n-1}}\frac{\prod_{1\leq j<k\leq n-1}| w_j- w_k|^2}{\prod_{l=1}^{n-1}|1-w_ls|^{2n-4}}\frac{1}{\prod_{l=1}^{n-1}|1-w_ls|^{np+4-2n}}dV(w_1,\dots,w_{n-1})\nonumber\\& \quad \lesssim\sum_{(l_1, l_2,\dots,l_{n-1})\in \mathcal S_{n-1}}\int_{\mathbb D^{n-1}}\frac{s^{-(n-1)(n-2)}}{\prod_{t=1}^{n-1}|1- w_{l_t}s|^{2n-2-2t}}.\frac{1}{\prod_{l=1}^{n-1}|1-w_ls|^{np+4-2n}}dV(w_1,\dots,w_{n-1})\nonumber\\& \quad \lesssim\int_{\mathbb D^{n-1}}\frac{1}{\prod_{l=1}^{n-1}|1-w_ls|^{np+2-2l}}dV(w_1,\dots,w_{n-1}).\nonumber\\ \end{align} $$
$$ \begin{align} &\|h_s\|^p_{L^p_{\text{sym}}(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2})}\nonumber\\& \quad \lesssim\int_{\mathbb D^{n-1}}\frac{\prod_{1\leq j<k\leq n-1}| w_j- w_k|^2}{\prod_{l=1}^{n-1}|1-w_ls|^{2n-4}}\frac{1}{\prod_{l=1}^{n-1}|1-w_ls|^{np+4-2n}}dV(w_1,\dots,w_{n-1})\nonumber\\& \quad \lesssim\sum_{(l_1, l_2,\dots,l_{n-1})\in \mathcal S_{n-1}}\int_{\mathbb D^{n-1}}\frac{s^{-(n-1)(n-2)}}{\prod_{t=1}^{n-1}|1- w_{l_t}s|^{2n-2-2t}}.\frac{1}{\prod_{l=1}^{n-1}|1-w_ls|^{np+4-2n}}dV(w_1,\dots,w_{n-1})\nonumber\\& \quad \lesssim\int_{\mathbb D^{n-1}}\frac{1}{\prod_{l=1}^{n-1}|1-w_ls|^{np+2-2l}}dV(w_1,\dots,w_{n-1}).\nonumber\\ \end{align} $$
For
![]() $p=\frac {2n}{n-1}$
,
$p=\frac {2n}{n-1}$
,
![]() $np+2-2l\geq np+2-2(n-1)>2$
. Thus the Forelli–Rudin estimates (2.8) imply
$np+2-2l\geq np+2-2(n-1)>2$
. Thus the Forelli–Rudin estimates (2.8) imply
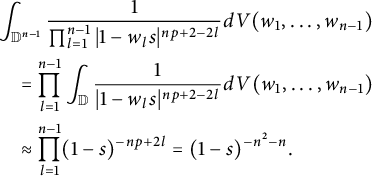 $$ \begin{align} &\int_{\mathbb D^{n-1}}\frac{1}{\prod_{l=1}^{n-1}|1-w_ls|^{np+2-2l}}dV(w_1,\dots,w_{n-1})\nonumber\\& \quad =\prod_{l=1}^{n-1}\int_{\mathbb D}\frac{1}{|1-w_ls|^{np+2-2l}}dV(w_1,\dots,w_{n-1})\nonumber\\& \quad \approx \prod_{l=1}^{n-1}(1-s)^{-np+2l}=(1-s)^{-n^2-n}. \end{align} $$
$$ \begin{align} &\int_{\mathbb D^{n-1}}\frac{1}{\prod_{l=1}^{n-1}|1-w_ls|^{np+2-2l}}dV(w_1,\dots,w_{n-1})\nonumber\\& \quad =\prod_{l=1}^{n-1}\int_{\mathbb D}\frac{1}{|1-w_ls|^{np+2-2l}}dV(w_1,\dots,w_{n-1})\nonumber\\& \quad \approx \prod_{l=1}^{n-1}(1-s)^{-np+2l}=(1-s)^{-n^2-n}. \end{align} $$
Hence
![]() $ \|h_s\|^p_{L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2})}\lesssim (1-s)^{-n^2-n}.$
$ \|h_s\|^p_{L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2})}\lesssim (1-s)^{-n^2-n}.$
Now we turn to compute
![]() $\tilde T^n(h_s)$
. Let I denote the identity operator. For the variable
$\tilde T^n(h_s)$
. Let I denote the identity operator. For the variable
![]() $w_j$
, let
$w_j$
, let
![]() $\mathcal D_{w_j}$
denote the partial differential operator
$\mathcal D_{w_j}$
denote the partial differential operator
 $$\begin{align*}\mathcal D_{w_j}=I+w_j\frac{\partial}{\partial w_j}.\end{align*}$$
$$\begin{align*}\mathcal D_{w_j}=I+w_j\frac{\partial}{\partial w_j}.\end{align*}$$
For any
![]() $k\in \mathbb N$
and holomorphic function
$k\in \mathbb N$
and holomorphic function
![]() $f(w)=\sum _{\alpha \in \mathbb N^n} c_{\alpha }w^{\alpha }$
on
$f(w)=\sum _{\alpha \in \mathbb N^n} c_{\alpha }w^{\alpha }$
on
![]() $\mathbb D^n$
,
$\mathbb D^n$
,
For each integer
![]() $k>2$
,
$k>2$
,
 $$ \begin{align*}\frac{1}{(1-w_js)^k}=\sum_{m=0}^{\infty}(m+1)_{k-1}s^mw_j^m=\sum_{m=0}^{\infty}(m+2)_{k-2}((m+1)s^mw_j^m),\end{align*} $$
$$ \begin{align*}\frac{1}{(1-w_js)^k}=\sum_{m=0}^{\infty}(m+1)_{k-1}s^mw_j^m=\sum_{m=0}^{\infty}(m+2)_{k-2}((m+1)s^mw_j^m),\end{align*} $$
where the Pochhammer symbol
![]() $(m+2)_{k-2}=(m+2)\dot (m+3)\dots (m+k-1)$
is a polynomial in m of degree
$(m+2)_{k-2}=(m+2)\dot (m+3)\dots (m+k-1)$
is a polynomial in m of degree
![]() $k-2$
. Thus, there exists a polynomial
$k-2$
. Thus, there exists a polynomial
![]() $q_{k-2}$
of degree
$q_{k-2}$
of degree
![]() $k-2$
such that
$k-2$
such that
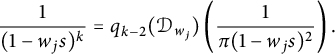 $$ \begin{align*}\frac{1}{(1-w_js)^k}=q_{k-2}(\mathcal D_{w_j})\left(\frac{1}{\pi(1-w_js)^2}\right).\end{align*} $$
$$ \begin{align*}\frac{1}{(1-w_js)^k}=q_{k-2}(\mathcal D_{w_j})\left(\frac{1}{\pi(1-w_js)^2}\right).\end{align*} $$
For holomorphic functions
![]() $f,g$
on
$f,g$
on
![]() $\mathbb D^n$
with
$\mathbb D^n$
with
![]() $f(w)=\sum _{\alpha }c_{\alpha }w^\alpha $
and
$f(w)=\sum _{\alpha }c_{\alpha }w^\alpha $
and
![]() $g(w)=\sum _{\alpha }d_{\alpha }w^\alpha $
,
$g(w)=\sum _{\alpha }d_{\alpha }w^\alpha $
,
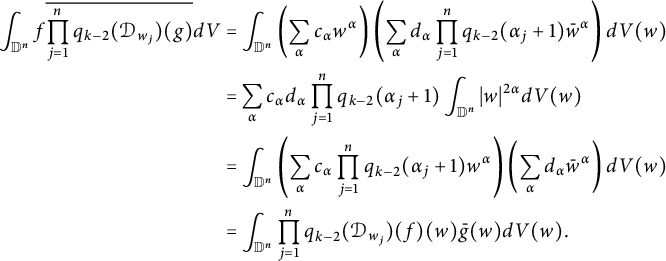 $$ \begin{align} \int_{\mathbb D^n}f\overline{\prod_{j=1}^{n}q_{k-2}(\mathcal D_{w_j})(g)}dV=&\int_{\mathbb D^n}\left(\sum_{\alpha}c_{\alpha}w^\alpha\right) \left(\sum_{\alpha}d_{\alpha}\prod_{j=1}^{n}q_{k-2}(\alpha_j+1)\bar w^\alpha\right)dV(w)\nonumber\\=&\sum_{\alpha}c_{\alpha}d_{\alpha}\prod_{j=1}^{n}q_{k-2}(\alpha_j+1)\int_{\mathbb D^n}|w|^{2\alpha}dV(w)\nonumber\\=&\int_{\mathbb D^n}\left(\sum_{\alpha}c_{\alpha}\prod_{j=1}^{n}q_{k-2}(\alpha_j+1)w^\alpha\right) \left(\sum_{\alpha}d_{\alpha}\bar w^\alpha\right)dV(w)\nonumber\\=&\int_{\mathbb D^n}\prod_{j=1}^{n}q_{k-2}(\mathcal D_{w_j})(f)(w)\bar g(w)dV(w). \end{align} $$
$$ \begin{align} \int_{\mathbb D^n}f\overline{\prod_{j=1}^{n}q_{k-2}(\mathcal D_{w_j})(g)}dV=&\int_{\mathbb D^n}\left(\sum_{\alpha}c_{\alpha}w^\alpha\right) \left(\sum_{\alpha}d_{\alpha}\prod_{j=1}^{n}q_{k-2}(\alpha_j+1)\bar w^\alpha\right)dV(w)\nonumber\\=&\sum_{\alpha}c_{\alpha}d_{\alpha}\prod_{j=1}^{n}q_{k-2}(\alpha_j+1)\int_{\mathbb D^n}|w|^{2\alpha}dV(w)\nonumber\\=&\int_{\mathbb D^n}\left(\sum_{\alpha}c_{\alpha}\prod_{j=1}^{n}q_{k-2}(\alpha_j+1)w^\alpha\right) \left(\sum_{\alpha}d_{\alpha}\bar w^\alpha\right)dV(w)\nonumber\\=&\int_{\mathbb D^n}\prod_{j=1}^{n}q_{k-2}(\mathcal D_{w_j})(f)(w)\bar g(w)dV(w). \end{align} $$
Therefore, we have
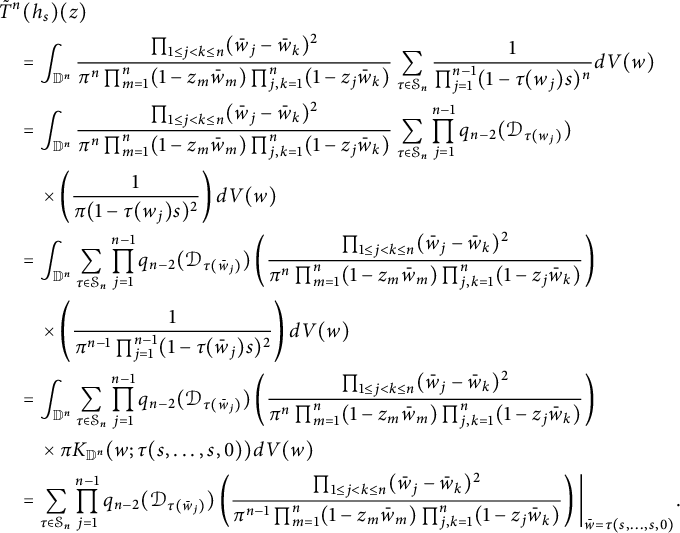 $$ \begin{align*} &\tilde T^n(h_s)(z)\nonumber\\& \quad =\int_{\mathbb D^n}\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^n\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\sum_{\tau\in \mathcal S_n}\frac{1}{\prod_{j=1}^{n-1}(1-\tau(w_j)s)^n}dV(w)\\& \quad =\int_{\mathbb D^n}\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^n\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\sum_{\tau\in \mathcal S_n}\prod_{j=1}^{n-1} q_{n-2}(\mathcal D_{\tau(w_j)})\\& \qquad \times \left(\frac{1}{\pi(1-\tau(w_j)s)^2}\right)dV(w) \\& \quad =\int_{\mathbb D^n}\sum_{\tau\in \mathcal S_n}\prod_{j=1}^{n-1} q_{n-2}(\mathcal D_{\tau(\bar w_j)})\left(\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^n\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\\& \qquad \times \left(\frac{1}{\pi^{n-1}\prod_{j=1}^{n-1}(1-\tau(\bar w_j)s)^2}\right)dV(w) \\& \quad =\int_{\mathbb D^n}\sum_{\tau\in \mathcal S_n}\prod_{j=1}^{n-1} q_{n-2}(\mathcal D_{\tau(\bar w_j)})\left(\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^n\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\\& \qquad \times \pi K_{\mathbb D^n}(w;\tau(s,\dots,s,0))dV(w) \\& \quad =\sum_{\tau\in \mathcal S_n}\prod_{j=1}^{n-1} q_{n-2}(\mathcal D_{\tau(\bar w_j)})\left(\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^{n-1}\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\bigg|_{\bar w=\tau(s,\dots,s,0)}. \end{align*} $$
$$ \begin{align*} &\tilde T^n(h_s)(z)\nonumber\\& \quad =\int_{\mathbb D^n}\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^n\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\sum_{\tau\in \mathcal S_n}\frac{1}{\prod_{j=1}^{n-1}(1-\tau(w_j)s)^n}dV(w)\\& \quad =\int_{\mathbb D^n}\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^n\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\sum_{\tau\in \mathcal S_n}\prod_{j=1}^{n-1} q_{n-2}(\mathcal D_{\tau(w_j)})\\& \qquad \times \left(\frac{1}{\pi(1-\tau(w_j)s)^2}\right)dV(w) \\& \quad =\int_{\mathbb D^n}\sum_{\tau\in \mathcal S_n}\prod_{j=1}^{n-1} q_{n-2}(\mathcal D_{\tau(\bar w_j)})\left(\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^n\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\\& \qquad \times \left(\frac{1}{\pi^{n-1}\prod_{j=1}^{n-1}(1-\tau(\bar w_j)s)^2}\right)dV(w) \\& \quad =\int_{\mathbb D^n}\sum_{\tau\in \mathcal S_n}\prod_{j=1}^{n-1} q_{n-2}(\mathcal D_{\tau(\bar w_j)})\left(\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^n\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\\& \qquad \times \pi K_{\mathbb D^n}(w;\tau(s,\dots,s,0))dV(w) \\& \quad =\sum_{\tau\in \mathcal S_n}\prod_{j=1}^{n-1} q_{n-2}(\mathcal D_{\tau(\bar w_j)})\left(\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^{n-1}\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\bigg|_{\bar w=\tau(s,\dots,s,0)}. \end{align*} $$
We claim that there is a constant
![]() $c_n$
such that
$c_n$
such that
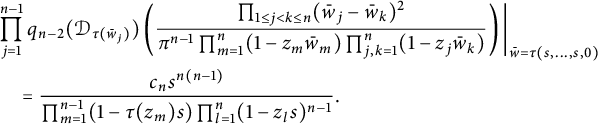 $$ \begin{align}&\prod_{j=1}^{n-1} q_{n-2}(\mathcal D_{\tau(\bar w_j)})\left(\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^{n-1}\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\bigg|_{\bar w=\tau(s,\dots,s,0)}\nonumber\\& \quad =\frac{c_ns^{n(n-1)}}{\prod_{m=1}^{n-1}(1-\tau(z_m)s)\prod_{l=1}^n(1-z_ls)^{n-1}}. \end{align} $$
$$ \begin{align}&\prod_{j=1}^{n-1} q_{n-2}(\mathcal D_{\tau(\bar w_j)})\left(\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^{n-1}\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\bigg|_{\bar w=\tau(s,\dots,s,0)}\nonumber\\& \quad =\frac{c_ns^{n(n-1)}}{\prod_{m=1}^{n-1}(1-\tau(z_m)s)\prod_{l=1}^n(1-z_ls)^{n-1}}. \end{align} $$
By symmetry, it suffices to show (4.14) for the case when
![]() $\tau $
is the identity map, i.e.,
$\tau $
is the identity map, i.e.,
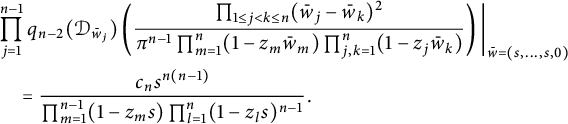 $$ \begin{align}&\prod_{j=1}^{n-1} q_{n-2}(\mathcal D_{\bar w_j})\left(\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^{n-1}\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\bigg|_{\bar w=(s,\dots,s,0)}\nonumber\\& \quad =\frac{c_ns^{n(n-1)}}{\prod_{m=1}^{n-1}(1-z_ms)\prod_{l=1}^n(1-z_ls)^{n-1}}.\end{align} $$
$$ \begin{align}&\prod_{j=1}^{n-1} q_{n-2}(\mathcal D_{\bar w_j})\left(\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^{n-1}\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\bigg|_{\bar w=(s,\dots,s,0)}\nonumber\\& \quad =\frac{c_ns^{n(n-1)}}{\prod_{m=1}^{n-1}(1-z_ms)\prod_{l=1}^n(1-z_ls)^{n-1}}.\end{align} $$
Set
![]() $\bar \partial _j=\frac {\partial }{\partial \bar w_j}$
. For a multi-index
$\bar \partial _j=\frac {\partial }{\partial \bar w_j}$
. For a multi-index
![]() $\mathbf l=(l_1,\dots ,l_{n})$
, set
$\mathbf l=(l_1,\dots ,l_{n})$
, set
![]() $\bar \partial ^{\mathbf l}=\bar \partial _1^{l_1}\dots \bar \partial _n^{l_n}$
. Then by the product rule,
$\bar \partial ^{\mathbf l}=\bar \partial _1^{l_1}\dots \bar \partial _n^{l_n}$
. Then by the product rule,
![]() $\mathcal D_{\bar w_j}^k=\sum _{l=0}^{k}c_{k,l}\bar w_j^l\bar \partial ^l_j$
. Therefore
$\mathcal D_{\bar w_j}^k=\sum _{l=0}^{k}c_{k,l}\bar w_j^l\bar \partial ^l_j$
. Therefore
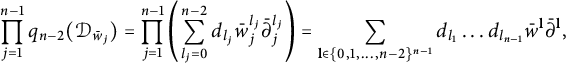 $$ \begin{align*}\prod_{j=1}^{n-1}q_{n-2}(\mathcal D_{\bar w_j})=\prod_{j=1}^{n-1}\left(\sum_{l_j=0}^{n-2}d_{l_j} \bar w_j^{l_j}\bar \partial^{l_j}_j\right)=\sum_{\mathbf l\in\{0,1,\dots, n-2\}^{n-1}}d_{l_1}\dots d_{l_{n-1}}\bar w^{\mathbf l}\bar \partial^{\mathbf l},\end{align*} $$
$$ \begin{align*}\prod_{j=1}^{n-1}q_{n-2}(\mathcal D_{\bar w_j})=\prod_{j=1}^{n-1}\left(\sum_{l_j=0}^{n-2}d_{l_j} \bar w_j^{l_j}\bar \partial^{l_j}_j\right)=\sum_{\mathbf l\in\{0,1,\dots, n-2\}^{n-1}}d_{l_1}\dots d_{l_{n-1}}\bar w^{\mathbf l}\bar \partial^{\mathbf l},\end{align*} $$
for some constants
![]() $d_{l_j}$
. Note that for
$d_{l_j}$
. Note that for
![]() $\mathbf l=(l_1,\dots ,l_{n-1})\in \{0,1,\dots , n-2\}^{n-1}$
,
$\mathbf l=(l_1,\dots ,l_{n-1})\in \{0,1,\dots , n-2\}^{n-1}$
,
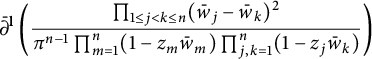 $$ \begin{align*}\bar \partial^{\mathbf l}\left(\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^{n-1}\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\end{align*} $$
$$ \begin{align*}\bar \partial^{\mathbf l}\left(\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^{n-1}\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\end{align*} $$
can be expressed as a linear combination of terms of the form
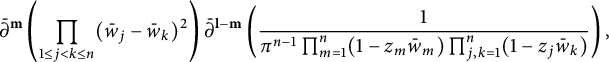 $$\begin{align*}\bar \partial^{\mathbf m}\left({\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}\right)\bar \partial^{\mathbf l-\mathbf m}\left(\frac{1}{\pi^{n-1}\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right),\end{align*}$$
$$\begin{align*}\bar \partial^{\mathbf m}\left({\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}\right)\bar \partial^{\mathbf l-\mathbf m}\left(\frac{1}{\pi^{n-1}\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right),\end{align*}$$
where
![]() $\mathbf m=(m_1,\dots ,m_{n-1})$
with
$\mathbf m=(m_1,\dots ,m_{n-1})$
with
![]() $m_j\leq l_j$
for all j and
$m_j\leq l_j$
for all j and
![]() $\mathbf l-\mathbf m=(l_1-m_1,\dots ,l_{n-1}-m_{n-1})$
.
$\mathbf l-\mathbf m=(l_1-m_1,\dots ,l_{n-1}-m_{n-1})$
.
Since
![]() $l_j\leq n-2$
for each j, the sum
$l_j\leq n-2$
for each j, the sum
Thus, the polynomial
![]() $\bar \partial ^{\mathbf m}\left ({\prod _{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}\right )$
is of total degree
$\bar \partial ^{\mathbf m}\left ({\prod _{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}\right )$
is of total degree
![]() $n(n-1)-|\mathbf m|$
which is at least
$n(n-1)-|\mathbf m|$
which is at least
![]() $n(n-1)-(n-1)(n-2)=2(n-1)$
. Note also that for
$n(n-1)-(n-1)(n-2)=2(n-1)$
. Note also that for
![]() $\bar w=(s,\dots ,s,0)$
, the factor
$\bar w=(s,\dots ,s,0)$
, the factor
![]() $(\bar w_j-\bar w_k)\neq 0$
if and only if either j or k equals n. It is not hard to see that the polynomial
$(\bar w_j-\bar w_k)\neq 0$
if and only if either j or k equals n. It is not hard to see that the polynomial
![]() $\prod _{k=1}^{n-1}(\bar w_k-\bar w_n)^2$
is the only divisor of
$\prod _{k=1}^{n-1}(\bar w_k-\bar w_n)^2$
is the only divisor of
![]() $\prod _{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2$
that has degree at least
$\prod _{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2$
that has degree at least
![]() $2(n-1)$
and does not vanish at
$2(n-1)$
and does not vanish at
![]() $(s,\dots ,s,0)$
. Hence,
$(s,\dots ,s,0)$
. Hence,
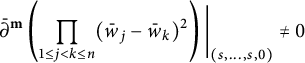 $$ \begin{align*}\bar \partial^{\mathbf m}\left({\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}\right)\bigg|_{(s,\dots,s,0)}\neq 0\end{align*} $$
$$ \begin{align*}\bar \partial^{\mathbf m}\left({\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}\right)\bigg|_{(s,\dots,s,0)}\neq 0\end{align*} $$
if and only if
![]() $|\mathbf m|=(n-2)(n-1)$
, i.e.,
$|\mathbf m|=(n-2)(n-1)$
, i.e.,
![]() $\mathbf m=(n-2,\dots ,n-2)$
. In this case, we have
$\mathbf m=(n-2,\dots ,n-2)$
. In this case, we have
 $$ \begin{align*}\prod_{j=1}^{n-1}\bar \partial_j^{n-2}\left({\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}\right)\bigg|_{(s,\dots,s,0)}=c_n\prod_{k=1}^{n-1}(\bar w_k-\bar w_n)^2|_{(s,\dots,s,0)}=c_ns^{2n-2}\end{align*} $$
$$ \begin{align*}\prod_{j=1}^{n-1}\bar \partial_j^{n-2}\left({\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}\right)\bigg|_{(s,\dots,s,0)}=c_n\prod_{k=1}^{n-1}(\bar w_k-\bar w_n)^2|_{(s,\dots,s,0)}=c_ns^{2n-2}\end{align*} $$
for some constant
![]() $c_n$
. Therefore,
$c_n$
. Therefore,
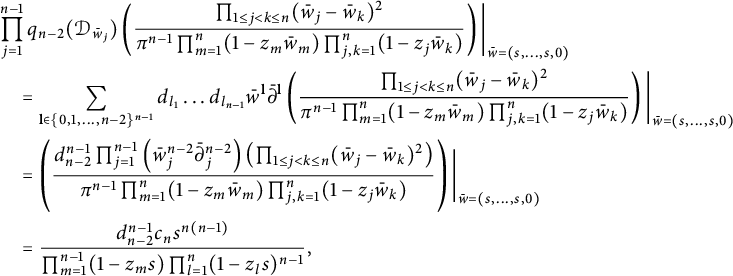 $$ \begin{align}&\prod_{j=1}^{n-1} q_{n-2}(\mathcal D_{\bar w_j})\left(\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^{n-1}\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\bigg|_{\bar w=(s,\dots,s,0)}\nonumber\\& \quad =\sum_{\mathbf l\in\{0,1,\dots, n-2\}^{n-1}}d_{l_1}\dots d_{l_{n-1}}\bar w^{\mathbf l}\bar \partial^{\mathbf l}\left(\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^{n-1}\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\bigg|_{\bar w=(s,\dots,s,0)}\nonumber\\& \quad =\left(\frac{d_{n-2}^{n-1}\prod_{j=1}^{n-1}\left(\bar w_j^{n-2}\bar \partial_j^{n-2}\right)\left({\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}\right)}{\pi^{n-1}\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\bigg|_{\bar w=(s,\dots,s,0)}\nonumber\\& \quad =\frac{d^{n-1}_{n-2}c_ns^{n(n-1)}}{\prod_{m=1}^{n-1}(1-z_ms)\prod_{l=1}^n(1-z_ls)^{n-1}},\nonumber\\ \end{align} $$
$$ \begin{align}&\prod_{j=1}^{n-1} q_{n-2}(\mathcal D_{\bar w_j})\left(\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^{n-1}\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\bigg|_{\bar w=(s,\dots,s,0)}\nonumber\\& \quad =\sum_{\mathbf l\in\{0,1,\dots, n-2\}^{n-1}}d_{l_1}\dots d_{l_{n-1}}\bar w^{\mathbf l}\bar \partial^{\mathbf l}\left(\frac{\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}{\pi^{n-1}\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\bigg|_{\bar w=(s,\dots,s,0)}\nonumber\\& \quad =\left(\frac{d_{n-2}^{n-1}\prod_{j=1}^{n-1}\left(\bar w_j^{n-2}\bar \partial_j^{n-2}\right)\left({\prod_{1\leq j< k\leq n}(\bar w_j-\bar w_k)^2}\right)}{\pi^{n-1}\prod_{m=1}^n(1-z_m\bar w_m)\prod_{j,k=1}^n(1-z_j\bar w_k)}\right)\bigg|_{\bar w=(s,\dots,s,0)}\nonumber\\& \quad =\frac{d^{n-1}_{n-2}c_ns^{n(n-1)}}{\prod_{m=1}^{n-1}(1-z_ms)\prod_{l=1}^n(1-z_ls)^{n-1}},\nonumber\\ \end{align} $$
which proves the claim (4.15) and gives
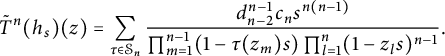 $$ \begin{align} \tilde T^n(h_s)(z)=\sum_{\tau\in\mathcal S_n}\frac{d^{n-1}_{n-2}c_ns^{n(n-1)}}{\prod_{m=1}^{n-1}(1-\tau(z_m)s)\prod_{l=1}^n(1-z_ls)^{n-1}}. \end{align} $$
$$ \begin{align} \tilde T^n(h_s)(z)=\sum_{\tau\in\mathcal S_n}\frac{d^{n-1}_{n-2}c_ns^{n(n-1)}}{\prod_{m=1}^{n-1}(1-\tau(z_m)s)\prod_{l=1}^n(1-z_ls)^{n-1}}. \end{align} $$
We next compute the norm of
![]() $\tilde T^n(h_s)$
$\tilde T^n(h_s)$
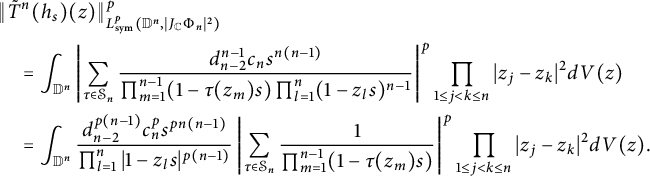 $$ \begin{align} &\| \tilde T^n(h_s)(z)\|^p_{L^p_{\text{sym}}(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2})}\nonumber\\& \quad =\int_{\mathbb D^n}\left|\sum_{\tau\in \mathcal S_n}\frac{d^{n-1}_{n-2}c_ns^{n(n-1)}}{\prod_{m=1}^{n-1}(1-\tau(z_m)s)\prod_{l=1}^n(1-z_ls)^{n-1}}\right|^p\prod_{1\leq j<k\leq n }| z_j- z_k|^2dV(z)\nonumber\\& \quad =\int_{\mathbb D^n}\frac{d^{p(n-1)}_{n-2}c_n^ps^{pn(n-1)}}{\prod_{l=1}^n|1-z_ls|^{p(n-1)}}\left|\sum_{\tau\in \mathcal S_n}\frac{1}{\prod_{m=1}^{n-1}(1-\tau(z_m)s)}\right|^p\prod_{1\leq j<k\leq n }| z_j- z_k|^2dV(z).\nonumber\\ \end{align} $$
$$ \begin{align} &\| \tilde T^n(h_s)(z)\|^p_{L^p_{\text{sym}}(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2})}\nonumber\\& \quad =\int_{\mathbb D^n}\left|\sum_{\tau\in \mathcal S_n}\frac{d^{n-1}_{n-2}c_ns^{n(n-1)}}{\prod_{m=1}^{n-1}(1-\tau(z_m)s)\prod_{l=1}^n(1-z_ls)^{n-1}}\right|^p\prod_{1\leq j<k\leq n }| z_j- z_k|^2dV(z)\nonumber\\& \quad =\int_{\mathbb D^n}\frac{d^{p(n-1)}_{n-2}c_n^ps^{pn(n-1)}}{\prod_{l=1}^n|1-z_ls|^{p(n-1)}}\left|\sum_{\tau\in \mathcal S_n}\frac{1}{\prod_{m=1}^{n-1}(1-\tau(z_m)s)}\right|^p\prod_{1\leq j<k\leq n }| z_j- z_k|^2dV(z).\nonumber\\ \end{align} $$
Set
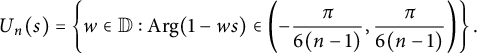 $$ \begin{align*}U_n(s)=\left\{w\in \mathbb D: \text{Arg}(1-ws)\in \left(-\frac{\pi}{6(n-1)},\frac{\pi}{6(n-1)}\right)\right\}.\end{align*} $$
$$ \begin{align*}U_n(s)=\left\{w\in \mathbb D: \text{Arg}(1-ws)\in \left(-\frac{\pi}{6(n-1)},\frac{\pi}{6(n-1)}\right)\right\}.\end{align*} $$
Then for any
![]() $z=(z_1,\dots ,z_n)\in (U_n(s))^n$
and
$z=(z_1,\dots ,z_n)\in (U_n(s))^n$
and
![]() $\tau \in \mathcal S_n$
,
$\tau \in \mathcal S_n$
,
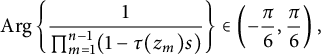 $$\begin{align*}\text{Arg}\left\{\frac{1}{\prod_{m=1}^{n-1}(1-\tau(z_m)s)}\right\}\in \left(-\frac{\pi}{6},\frac{\pi}{6}\right),\end{align*}$$
$$\begin{align*}\text{Arg}\left\{\frac{1}{\prod_{m=1}^{n-1}(1-\tau(z_m)s)}\right\}\in \left(-\frac{\pi}{6},\frac{\pi}{6}\right),\end{align*}$$
which yields that
 $$\begin{align*}\left|\sum_{\tau\in \mathcal S_n}\frac{1}{\prod_{m=1}^{n-1}(1-\tau(z_m)s)}\right|\gtrsim \frac{1}{\prod_{m=1}^{n-1}|1-z_ms|}.\end{align*}$$
$$\begin{align*}\left|\sum_{\tau\in \mathcal S_n}\frac{1}{\prod_{m=1}^{n-1}(1-\tau(z_m)s)}\right|\gtrsim \frac{1}{\prod_{m=1}^{n-1}|1-z_ms|}.\end{align*}$$
Using this inequality, we have
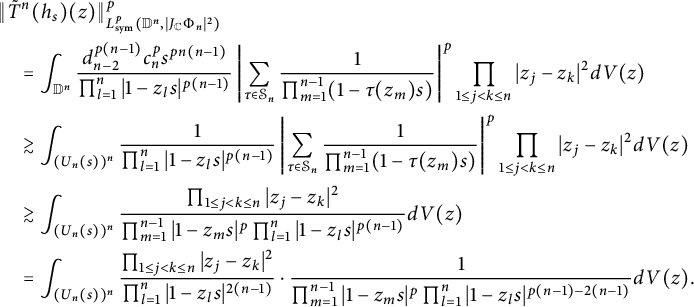 $$ \begin{align} &\| \tilde T^n(h_s)(z)\|^p_{L^p_{\text{sym}}(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2})}\nonumber\\& \quad =\int_{\mathbb D^n}\frac{d^{p(n-1)}_{n-2}c_n^ps^{pn(n-1)}}{\prod_{l=1}^n|1-z_ls|^{p(n-1)}}\left|\sum_{\tau\in \mathcal S_n}\frac{1}{\prod_{m=1}^{n-1}(1-\tau(z_m)s)}\right|^p\prod_{1\leq j<k\leq n }| z_j- z_k|^2dV(z)\nonumber\\& \quad \gtrsim\int_{(U_n(s))^n}\frac{1}{\prod_{l=1}^n|1-z_ls|^{p(n-1)}}\left|\sum_{\tau\in \mathcal S_n}\frac{1}{\prod_{m=1}^{n-1}(1-\tau(z_m)s)}\right|^p\prod_{1\leq j<k\leq n }| z_j- z_k|^2dV(z)\nonumber\\& \quad \gtrsim\int_{(U_n(s))^n}\frac{\prod_{1\leq j<k\leq n }| z_j- z_k|^2}{\prod_{m=1}^{n-1}|1-z_ms|^p\prod_{l=1}^n|1-z_ls|^{p(n-1)}}dV(z)\nonumber\\& \quad =\int_{(U_n(s))^n}\frac{\prod_{1\leq j<k\leq n }| z_j- z_k|^2}{\prod_{l=1}^n|1-z_ls|^{2(n-1)}}\cdot\frac{1}{\prod_{m=1}^{n-1}|1-z_ms|^p\prod_{l=1}^n|1-z_ls|^{p(n-1)-2(n-1)}}dV(z).\nonumber\\ \end{align} $$
$$ \begin{align} &\| \tilde T^n(h_s)(z)\|^p_{L^p_{\text{sym}}(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2})}\nonumber\\& \quad =\int_{\mathbb D^n}\frac{d^{p(n-1)}_{n-2}c_n^ps^{pn(n-1)}}{\prod_{l=1}^n|1-z_ls|^{p(n-1)}}\left|\sum_{\tau\in \mathcal S_n}\frac{1}{\prod_{m=1}^{n-1}(1-\tau(z_m)s)}\right|^p\prod_{1\leq j<k\leq n }| z_j- z_k|^2dV(z)\nonumber\\& \quad \gtrsim\int_{(U_n(s))^n}\frac{1}{\prod_{l=1}^n|1-z_ls|^{p(n-1)}}\left|\sum_{\tau\in \mathcal S_n}\frac{1}{\prod_{m=1}^{n-1}(1-\tau(z_m)s)}\right|^p\prod_{1\leq j<k\leq n }| z_j- z_k|^2dV(z)\nonumber\\& \quad \gtrsim\int_{(U_n(s))^n}\frac{\prod_{1\leq j<k\leq n }| z_j- z_k|^2}{\prod_{m=1}^{n-1}|1-z_ms|^p\prod_{l=1}^n|1-z_ls|^{p(n-1)}}dV(z)\nonumber\\& \quad =\int_{(U_n(s))^n}\frac{\prod_{1\leq j<k\leq n }| z_j- z_k|^2}{\prod_{l=1}^n|1-z_ls|^{2(n-1)}}\cdot\frac{1}{\prod_{m=1}^{n-1}|1-z_ms|^p\prod_{l=1}^n|1-z_ls|^{p(n-1)-2(n-1)}}dV(z).\nonumber\\ \end{align} $$
By a similar
![]() $(n-1)$
-step partial fraction procedure, we obtain the following analogue of (4.10)
$(n-1)$
-step partial fraction procedure, we obtain the following analogue of (4.10)
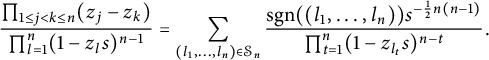 $$\begin{align*}\frac{\prod_{1\leq j<k\leq n }(z_j- z_k)}{\prod_{l=1}^n(1-z_ls)^{n-1}}=\sum_{(l_1,\dots,l_n)\in\mathcal S_n}\frac{\text{sgn}((l_1,\dots,l_n))s^{-\frac{1}{2}n(n-1)}}{\prod_{t=1}^n(1-z_{l_t}s)^{n-t}}.\end{align*}$$
$$\begin{align*}\frac{\prod_{1\leq j<k\leq n }(z_j- z_k)}{\prod_{l=1}^n(1-z_ls)^{n-1}}=\sum_{(l_1,\dots,l_n)\in\mathcal S_n}\frac{\text{sgn}((l_1,\dots,l_n))s^{-\frac{1}{2}n(n-1)}}{\prod_{t=1}^n(1-z_{l_t}s)^{n-t}}.\end{align*}$$
Hence (4.19) becomes
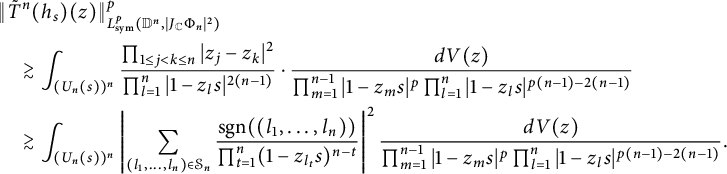 $$ \begin{align} &\| \tilde T^n(h_s)(z)\|^p_{L^p_{\text{sym}}(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2})}\nonumber\\& \quad \gtrsim\int_{(U_n(s))^n}\frac{\prod_{1\leq j<k\leq n }| z_j- z_k|^2}{\prod_{l=1}^n|1-z_ls|^{2(n-1)}}\cdot\frac{dV(z)}{\prod_{m=1}^{n-1}|1-z_ms|^p\prod_{l=1}^n|1-z_ls|^{p(n-1)-2(n-1)}}\nonumber\\& \quad \gtrsim \int_{(U_n(s))^n}\left|\sum_{(l_1,\dots,l_n)\in\mathcal S_n}\frac{\text{sgn}((l_1,\dots,l_n))}{\prod_{t=1}^n(1-z_{l_t}s)^{n-t}}\right|^2\frac{dV(z)}{\prod_{m=1}^{n-1}|1-z_ms|^p \prod_{l=1}^n|1-z_ls|^{p(n-1)-2(n-1)}}.\nonumber\\ \end{align} $$
$$ \begin{align} &\| \tilde T^n(h_s)(z)\|^p_{L^p_{\text{sym}}(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2})}\nonumber\\& \quad \gtrsim\int_{(U_n(s))^n}\frac{\prod_{1\leq j<k\leq n }| z_j- z_k|^2}{\prod_{l=1}^n|1-z_ls|^{2(n-1)}}\cdot\frac{dV(z)}{\prod_{m=1}^{n-1}|1-z_ms|^p\prod_{l=1}^n|1-z_ls|^{p(n-1)-2(n-1)}}\nonumber\\& \quad \gtrsim \int_{(U_n(s))^n}\left|\sum_{(l_1,\dots,l_n)\in\mathcal S_n}\frac{\text{sgn}((l_1,\dots,l_n))}{\prod_{t=1}^n(1-z_{l_t}s)^{n-t}}\right|^2\frac{dV(z)}{\prod_{m=1}^{n-1}|1-z_ms|^p \prod_{l=1}^n|1-z_ls|^{p(n-1)-2(n-1)}}.\nonumber\\ \end{align} $$
We further restrict our region of integration to obtain more precise estimates. For
![]() $j\in \{1,\dots ,n\}$
and
$j\in \{1,\dots ,n\}$
and
![]() $s\in (1-(5n!)^{-2n},1)$
, we set
$s\in (1-(5n!)^{-2n},1)$
, we set
and set
![]() $\mathbf U(s)=U_n(s,1)\times U_n(s,2)\times \dots \times U_n(s,n).$
It is worth noting that we implement a positive lower bound
$\mathbf U(s)=U_n(s,1)\times U_n(s,2)\times \dots \times U_n(s,n).$
It is worth noting that we implement a positive lower bound
![]() $1-(5n!)^{-2n}$
for s here so that
$1-(5n!)^{-2n}$
for s here so that
![]() $U_n(s,j)$
is nonempty and
$U_n(s,j)$
is nonempty and
![]() $\mathbf U(s)$
is asymmetric in its components. As the reader will see, we need this extra restriction for s but not when
$\mathbf U(s)$
is asymmetric in its components. As the reader will see, we need this extra restriction for s but not when
![]() $n=2$
since in higher dimensions, the desired integral estimates cannot be achieved solely by Forelli–Rudin estimate. The asymmetry of
$n=2$
since in higher dimensions, the desired integral estimates cannot be achieved solely by Forelli–Rudin estimate. The asymmetry of
![]() $\mathbf U(s)$
is also used.
$\mathbf U(s)$
is also used.
By a polar coordinate computation,
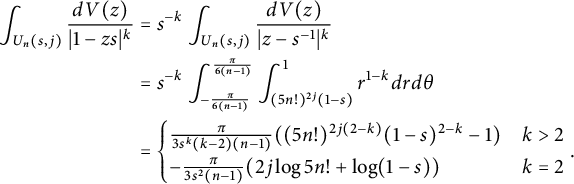 $$ \begin{align} \int_{U_n(s,j)}\frac{dV(z)}{|1-zs|^k}&=s^{-k}\int_{U_n(s,j)}\frac{dV(z)}{|z-s^{-1}|^k}\nonumber\\&=s^{-k}\int_{-\frac{\pi}{6(n-1)}}^{\frac{\pi}{6(n-1)}}\int_{(5n!)^{2j}(1-s)}^{1}r^{1-k}drd\theta\nonumber\\&=\begin{cases} \frac{\pi}{3s^k(k-2)(n-1)}((5n!)^{2j(2-k)}(1-s)^{2-k}-1)& k>2\\ -\frac{\pi}{3s^2(n-1)}(2j\log 5n!+\log(1-s))& k=2 \end{cases}.\end{align} $$
$$ \begin{align} \int_{U_n(s,j)}\frac{dV(z)}{|1-zs|^k}&=s^{-k}\int_{U_n(s,j)}\frac{dV(z)}{|z-s^{-1}|^k}\nonumber\\&=s^{-k}\int_{-\frac{\pi}{6(n-1)}}^{\frac{\pi}{6(n-1)}}\int_{(5n!)^{2j}(1-s)}^{1}r^{1-k}drd\theta\nonumber\\&=\begin{cases} \frac{\pi}{3s^k(k-2)(n-1)}((5n!)^{2j(2-k)}(1-s)^{2-k}-1)& k>2\\ -\frac{\pi}{3s^2(n-1)}(2j\log 5n!+\log(1-s))& k=2 \end{cases}.\end{align} $$
For functions
![]() $f(s)$
and
$f(s)$
and
![]() $g(s)$
, we write
$g(s)$
, we write
![]() $f(s)\sim g(s)$
if
$f(s)\sim g(s)$
if
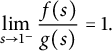 $$\begin{align*}\lim_{s\to 1^-}\frac{f(s)}{g(s)}=1.\end{align*}$$
$$\begin{align*}\lim_{s\to 1^-}\frac{f(s)}{g(s)}=1.\end{align*}$$
Then, (4.21) yields
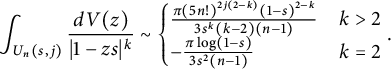 $$ \begin{align}\int_{U_n(s,j)}\frac{dV(z)}{|1-zs|^k}\sim \begin{cases} \frac{\pi(5n!)^{2j(2-k)}(1-s)^{2-k}}{3s^k(k-2)(n-1)}& k>2\\ -\frac{\pi\log(1-s)}{3s^2(n-1)}& k=2 \end{cases}.\end{align} $$
$$ \begin{align}\int_{U_n(s,j)}\frac{dV(z)}{|1-zs|^k}\sim \begin{cases} \frac{\pi(5n!)^{2j(2-k)}(1-s)^{2-k}}{3s^k(k-2)(n-1)}& k>2\\ -\frac{\pi\log(1-s)}{3s^2(n-1)}& k=2 \end{cases}.\end{align} $$
Recall that for
![]() $\tau \in \mathcal S_n$
, we let
$\tau \in \mathcal S_n$
, we let
![]() $\tau (j)$
be the index satisfying
$\tau (j)$
be the index satisfying
![]() $z_{\tau (j)}=\tau (z_j)$
. For
$z_{\tau (j)}=\tau (z_j)$
. For
![]() $p=\frac {2n}{n-1}$
, the triangle inequality and Cauchy–Schwarz inequality implies
$p=\frac {2n}{n-1}$
, the triangle inequality and Cauchy–Schwarz inequality implies
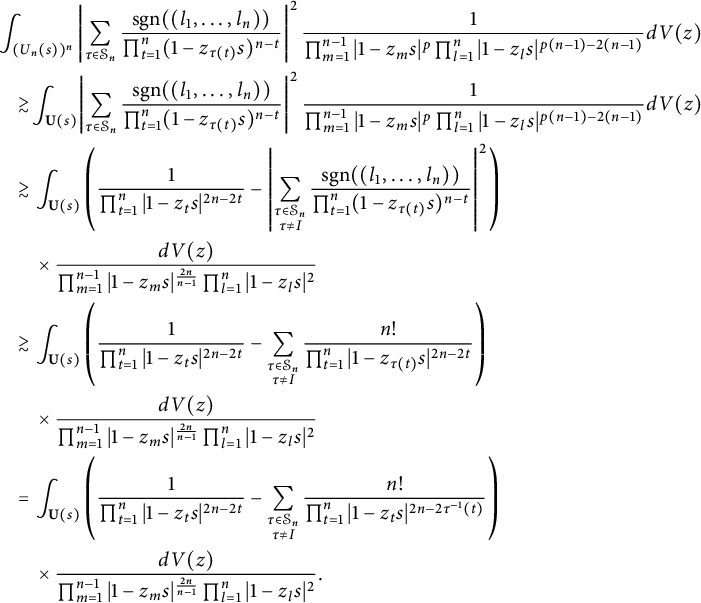 $$ \begin{align*} &\!\!\int_{(U_n(s))^n}\left|\sum_{\tau\in\mathcal S_n}\frac{\text{sgn}((l_1,\dots,l_n))}{\prod_{t=1}^n(1-z_{\tau(t)}s)^{n-t}}\right|^2\frac{1}{\prod_{m=1}^{n-1}|1-z_ms|^p \prod_{l=1}^n|1-z_ls|^{p(n-1)-2(n-1)}}dV(z)\\& \quad \!\!\!\gtrsim\!\int_{\mathbf U(s)}\!\left|\sum_{\tau\in\mathcal S_n}\frac{\text{sgn}((l_1,\dots,l_n))}{\prod_{t=1}^n(1-z_{\tau(t)}s)^{n-t}}\right|^2 \frac{1}{\prod_{m=1}^{n-1}|1-z_ms|^p \prod_{l=1}^n|1-z_ls|^{p(n-1)-2(n-1)}}dV(z)\\& \quad \!\!\!\gtrsim\int_{\mathbf U(s)}\left(\frac{1}{\prod_{t=1}^n|1-z_{t}s|^{2n-2t}}-\left|\sum_{\substack{\tau\in\mathcal S_n\\ \tau\neq I}}\frac{\text{sgn}((l_1,\dots,l_n))}{\prod_{t=1}^n(1-z_{\tau(t)}s)^{n-t}}\right|^2\right)\\& \qquad \!\!\!\times \frac{dV(z)}{\prod_{m=1}^{n-1}|1-z_ms|^{\frac{2n}{n-1}} \prod_{l=1}^n|1-z_ls|^{2}}\\& \quad \!\!\!\gtrsim\int_{\mathbf U(s)}\left(\frac{1}{\prod_{t=1}^n|1-z_{t}s|^{2n-2t}}-\sum_{\substack{\tau\in\mathcal S_n\\ \tau\neq I}}\frac{n!}{\prod_{t=1}^n|1-z_{\tau(t)}s|^{2n-2t}}\right)\\& \qquad \!\!\!\times \frac{dV(z)}{\prod_{m=1}^{n-1}|1-z_ms|^{\frac{2n}{n-1}}\prod_{l=1}^n|1-z_ls|^{2}}\\& \quad \!\!\!=\int_{\mathbf U(s)}\left(\frac{1}{\prod_{t=1}^n|1-z_{t}s|^{2n-2t}}-\sum_{\substack{\tau\in\mathcal S_n\\ \tau\neq I}}\frac{n!}{\prod_{t=1}^n|1-z_ts|^{2n-2\tau^{-1}(t)}}\right)\\& \qquad \!\!\!\times \frac{dV(z)}{\prod_{m=1}^{n-1}|1-z_ms|^{\frac{2n}{n-1}}\prod_{l=1}^n|1-z_ls|^{2}}. \end{align*} $$
$$ \begin{align*} &\!\!\int_{(U_n(s))^n}\left|\sum_{\tau\in\mathcal S_n}\frac{\text{sgn}((l_1,\dots,l_n))}{\prod_{t=1}^n(1-z_{\tau(t)}s)^{n-t}}\right|^2\frac{1}{\prod_{m=1}^{n-1}|1-z_ms|^p \prod_{l=1}^n|1-z_ls|^{p(n-1)-2(n-1)}}dV(z)\\& \quad \!\!\!\gtrsim\!\int_{\mathbf U(s)}\!\left|\sum_{\tau\in\mathcal S_n}\frac{\text{sgn}((l_1,\dots,l_n))}{\prod_{t=1}^n(1-z_{\tau(t)}s)^{n-t}}\right|^2 \frac{1}{\prod_{m=1}^{n-1}|1-z_ms|^p \prod_{l=1}^n|1-z_ls|^{p(n-1)-2(n-1)}}dV(z)\\& \quad \!\!\!\gtrsim\int_{\mathbf U(s)}\left(\frac{1}{\prod_{t=1}^n|1-z_{t}s|^{2n-2t}}-\left|\sum_{\substack{\tau\in\mathcal S_n\\ \tau\neq I}}\frac{\text{sgn}((l_1,\dots,l_n))}{\prod_{t=1}^n(1-z_{\tau(t)}s)^{n-t}}\right|^2\right)\\& \qquad \!\!\!\times \frac{dV(z)}{\prod_{m=1}^{n-1}|1-z_ms|^{\frac{2n}{n-1}} \prod_{l=1}^n|1-z_ls|^{2}}\\& \quad \!\!\!\gtrsim\int_{\mathbf U(s)}\left(\frac{1}{\prod_{t=1}^n|1-z_{t}s|^{2n-2t}}-\sum_{\substack{\tau\in\mathcal S_n\\ \tau\neq I}}\frac{n!}{\prod_{t=1}^n|1-z_{\tau(t)}s|^{2n-2t}}\right)\\& \qquad \!\!\!\times \frac{dV(z)}{\prod_{m=1}^{n-1}|1-z_ms|^{\frac{2n}{n-1}}\prod_{l=1}^n|1-z_ls|^{2}}\\& \quad \!\!\!=\int_{\mathbf U(s)}\left(\frac{1}{\prod_{t=1}^n|1-z_{t}s|^{2n-2t}}-\sum_{\substack{\tau\in\mathcal S_n\\ \tau\neq I}}\frac{n!}{\prod_{t=1}^n|1-z_ts|^{2n-2\tau^{-1}(t)}}\right)\\& \qquad \!\!\!\times \frac{dV(z)}{\prod_{m=1}^{n-1}|1-z_ms|^{\frac{2n}{n-1}}\prod_{l=1}^n|1-z_ls|^{2}}. \end{align*} $$
We claim that in the integral above, the first term will dominate the rest terms, and thus determines the size of the entire integral. We start by showing that the first term dominates the sum of those terms with
![]() $\tau ^{-1}(n)\neq n$
. Note that
$\tau ^{-1}(n)\neq n$
. Note that
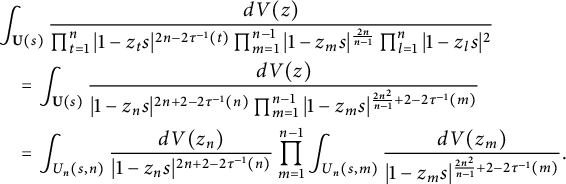 $$ \begin{align} &\int_{\mathbf U(s)}\frac{dV(z)}{\prod_{t=1}^n|1-z_ts|^{2n-2\tau^{-1}(t)}\prod_{m=1}^{n-1}|1-z_ms|^{\frac{2n}{n-1}}\prod_{l=1}^n|1-z_ls|^{2}}\nonumber\\& \quad = \int_{\mathbf U(s)}\frac{dV(z)}{|1-z_ns|^{2n+2-2\tau^{-1}(n)}\prod_{m=1}^{n-1}|1-z_ms|^{\frac{2n^2}{n-1}+2-2\tau^{-1}(m)}}\nonumber\\& \quad = \int_{U_n(s,n)}\frac{dV(z_n)}{|1-z_ns|^{2n+2-2\tau^{-1}(n)}}\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2\tau^{-1}(m)}}. \end{align} $$
$$ \begin{align} &\int_{\mathbf U(s)}\frac{dV(z)}{\prod_{t=1}^n|1-z_ts|^{2n-2\tau^{-1}(t)}\prod_{m=1}^{n-1}|1-z_ms|^{\frac{2n}{n-1}}\prod_{l=1}^n|1-z_ls|^{2}}\nonumber\\& \quad = \int_{\mathbf U(s)}\frac{dV(z)}{|1-z_ns|^{2n+2-2\tau^{-1}(n)}\prod_{m=1}^{n-1}|1-z_ms|^{\frac{2n^2}{n-1}+2-2\tau^{-1}(m)}}\nonumber\\& \quad = \int_{U_n(s,n)}\frac{dV(z_n)}{|1-z_ns|^{2n+2-2\tau^{-1}(n)}}\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2\tau^{-1}(m)}}. \end{align} $$
Since
![]() $1\leq m\leq n-1$
, the denominator factor
$1\leq m\leq n-1$
, the denominator factor
![]() $|1-z_ms|$
in (4.23) has power strictly greater than 2. The factor
$|1-z_ms|$
in (4.23) has power strictly greater than 2. The factor
![]() $|1-z_ns|$
has power 2 only if
$|1-z_ns|$
has power 2 only if
![]() $\tau ^{-1}(n)=n$
, or equivalently
$\tau ^{-1}(n)=n$
, or equivalently
![]() $\tau (z_n)=z_n$
. By the Forelli–Rudin estimates (2.8) and the fact that
$\tau (z_n)=z_n$
. By the Forelli–Rudin estimates (2.8) and the fact that
![]() $\{\tau ^{-1}(1),\dots ,\tau ^{-1}(n)\}=\{1,\dots ,n\}$
,
$\{\tau ^{-1}(1),\dots ,\tau ^{-1}(n)\}=\{1,\dots ,n\}$
,
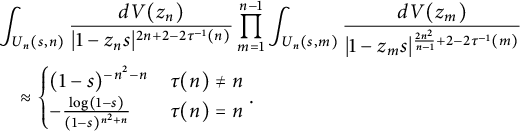 $$ \begin{align} &\int_{U_n(s,n)}\frac{dV(z_n)}{|1-z_ns|^{2n+2-2\tau^{-1}(n)}}\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2\tau^{-1}(m)}} \nonumber\\& \quad \approx\begin{cases} (1-s)^{-n^2-n}& \tau(n)\neq n\\ -\frac{\log(1-s)}{(1-s)^{n^2+n}}& \tau(n)=n \end{cases}. \end{align} $$
$$ \begin{align} &\int_{U_n(s,n)}\frac{dV(z_n)}{|1-z_ns|^{2n+2-2\tau^{-1}(n)}}\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2\tau^{-1}(m)}} \nonumber\\& \quad \approx\begin{cases} (1-s)^{-n^2-n}& \tau(n)\neq n\\ -\frac{\log(1-s)}{(1-s)^{n^2+n}}& \tau(n)=n \end{cases}. \end{align} $$
Thus, for s sufficiently close to
![]() $1$
, the integral in (4.23) with
$1$
, the integral in (4.23) with
![]() $\tau (n)=n$
dominates the ones with
$\tau (n)=n$
dominates the ones with
![]() $\tau (n)\neq n$
. Therefore, we can further assume that
$\tau (n)\neq n$
. Therefore, we can further assume that
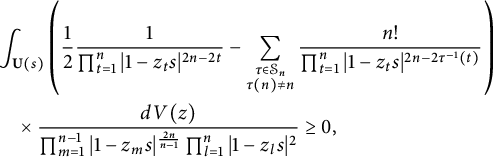 $$\begin{align*}&\int_{\mathbf U(s)}\left(\frac{1}{2}\frac{1}{\prod_{t=1}^n|1-z_{t}s|^{2n-2t}}-\sum_{\substack{\tau\in\mathcal S_n\\ \tau(n)\neq n}}\frac{n!}{\prod_{t=1}^n|1-z_ts|^{2n-2\tau^{-1}(t)}}\right)\\& \quad \times \frac{dV(z)}{\prod_{m=1}^{n-1}|1-z_ms|^{\frac{2n}{n-1}} \prod_{l=1}^n|1-z_ls|^2}\geq0, \end{align*}$$
$$\begin{align*}&\int_{\mathbf U(s)}\left(\frac{1}{2}\frac{1}{\prod_{t=1}^n|1-z_{t}s|^{2n-2t}}-\sum_{\substack{\tau\in\mathcal S_n\\ \tau(n)\neq n}}\frac{n!}{\prod_{t=1}^n|1-z_ts|^{2n-2\tau^{-1}(t)}}\right)\\& \quad \times \frac{dV(z)}{\prod_{m=1}^{n-1}|1-z_ms|^{\frac{2n}{n-1}} \prod_{l=1}^n|1-z_ls|^2}\geq0, \end{align*}$$
which implies
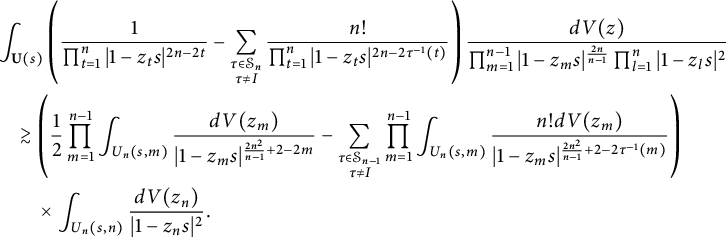 $$ \begin{align} &\int_{\mathbf U(s)}\left(\frac{1}{\prod_{t=1}^n|1-z_{t}s|^{2n-2t}}-\sum_{\substack{\tau\in\mathcal S_n\\ \tau\neq I}}\frac{n!}{\prod_{t=1}^n|1-z_ts|^{2n-2\tau^{-1}(t)}}\right)\frac{dV(z)}{\prod_{m=1}^{n-1}|1-z_ms|^{\frac{2n}{n-1}} \prod_{l=1}^n|1-z_ls|^{2}}\nonumber\\& \quad \gtrsim\left(\frac{1}{2}\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2m}}-\sum_{\substack{\tau\in\mathcal S_{n-1}\\ \tau\neq I}}\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{n!dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2\tau^{-1}(m)}}\right)\nonumber\\& \qquad \times \int_{U_n(s,n)}\frac{dV(z_n)}{|1-z_ns|^{2}}. \nonumber\\ \end{align} $$
$$ \begin{align} &\int_{\mathbf U(s)}\left(\frac{1}{\prod_{t=1}^n|1-z_{t}s|^{2n-2t}}-\sum_{\substack{\tau\in\mathcal S_n\\ \tau\neq I}}\frac{n!}{\prod_{t=1}^n|1-z_ts|^{2n-2\tau^{-1}(t)}}\right)\frac{dV(z)}{\prod_{m=1}^{n-1}|1-z_ms|^{\frac{2n}{n-1}} \prod_{l=1}^n|1-z_ls|^{2}}\nonumber\\& \quad \gtrsim\left(\frac{1}{2}\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2m}}-\sum_{\substack{\tau\in\mathcal S_{n-1}\\ \tau\neq I}}\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{n!dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2\tau^{-1}(m)}}\right)\nonumber\\& \qquad \times \int_{U_n(s,n)}\frac{dV(z_n)}{|1-z_ns|^{2}}. \nonumber\\ \end{align} $$
Now we turn to show that the positive term in the last line of (4.25) also dominates the rest terms. Since all these terms share the same
![]() $z_n$
part, the estimate (4.24) is no longer able to distinguish one from another. Thus here, we will make use of the asymmetry of
$z_n$
part, the estimate (4.24) is no longer able to distinguish one from another. Thus here, we will make use of the asymmetry of
![]() $\mathbf U(s)$
in
$\mathbf U(s)$
in
![]() $z_j$
variables to prove the claim.
$z_j$
variables to prove the claim.
By (4.22), we have
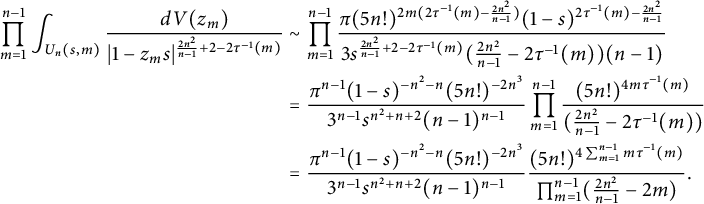 $$ \begin{align} \prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2\tau^{-1}(m)}}&\sim\prod_{m=1}^{n-1} \frac{\pi(5n!)^{2m(2\tau^{-1}(m)-\frac{2n^2}{n-1})}(1-s)^{2\tau^{-1}(m)-\frac{2n^2}{n-1}}}{3s^{\frac{2n^2}{n-1}+2-2\tau^{-1}(m)} (\frac{2n^2}{n-1}-2\tau^{-1}(m))(n-1)}\nonumber\\&=\frac{\pi^{n-1}(1-s)^{-n^2-n}(5n!)^{-2n^3}}{3^{n-1}s^{n^2+n+2}(n-1)^{n-1}} \prod_{m=1}^{n-1}\frac{(5n!)^{4m\tau^{-1}(m)}}{(\frac{2n^2}{n-1}-2\tau^{-1}(m))}\nonumber\\&=\frac{\pi^{n-1}(1-s)^{-n^2-n}(5n!)^{-2n^3}}{3^{n-1}s^{n^2+n+2}(n-1)^{n-1}}\frac{(5n!)^{4\sum_{m=1}^{n-1}m \tau^{-1}(m)}}{\prod_{m=1}^{n-1}(\frac{2n^2}{n-1}-2m)}. \end{align} $$
$$ \begin{align} \prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2\tau^{-1}(m)}}&\sim\prod_{m=1}^{n-1} \frac{\pi(5n!)^{2m(2\tau^{-1}(m)-\frac{2n^2}{n-1})}(1-s)^{2\tau^{-1}(m)-\frac{2n^2}{n-1}}}{3s^{\frac{2n^2}{n-1}+2-2\tau^{-1}(m)} (\frac{2n^2}{n-1}-2\tau^{-1}(m))(n-1)}\nonumber\\&=\frac{\pi^{n-1}(1-s)^{-n^2-n}(5n!)^{-2n^3}}{3^{n-1}s^{n^2+n+2}(n-1)^{n-1}} \prod_{m=1}^{n-1}\frac{(5n!)^{4m\tau^{-1}(m)}}{(\frac{2n^2}{n-1}-2\tau^{-1}(m))}\nonumber\\&=\frac{\pi^{n-1}(1-s)^{-n^2-n}(5n!)^{-2n^3}}{3^{n-1}s^{n^2+n+2}(n-1)^{n-1}}\frac{(5n!)^{4\sum_{m=1}^{n-1}m \tau^{-1}(m)}}{\prod_{m=1}^{n-1}(\frac{2n^2}{n-1}-2m)}. \end{align} $$
Hence, for any permutation
![]() $\tau \in \mathcal S_{n-1}$
with
$\tau \in \mathcal S_{n-1}$
with
![]() $\tau \neq I$
,
$\tau \neq I$
,
 $$ \begin{align} \frac{\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2m}}}{\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2\tau^{-1}(m)}}}&\sim(5n!)^{4\sum_{m=1}^{n-1}(m^2-m\tau^{-1}(m))}\geq (4n!)^4. \end{align} $$
$$ \begin{align} \frac{\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2m}}}{\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2\tau^{-1}(m)}}}&\sim(5n!)^{4\sum_{m=1}^{n-1}(m^2-m\tau^{-1}(m))}\geq (4n!)^4. \end{align} $$
Here
![]() $\sum _{m=1}^{n-1}(m^2-m\tau ^{-1}(m))\geq 1$
follows by Cauchy–Schwarz inequality and the fact that the sum
$\sum _{m=1}^{n-1}(m^2-m\tau ^{-1}(m))\geq 1$
follows by Cauchy–Schwarz inequality and the fact that the sum
![]() $\sum _{m=1}^{n-1}(m^2-m\tau ^{-1}(m))$
is an integer. Substituting these estimates into (4.25), we finally obtain
$\sum _{m=1}^{n-1}(m^2-m\tau ^{-1}(m))$
is an integer. Substituting these estimates into (4.25), we finally obtain
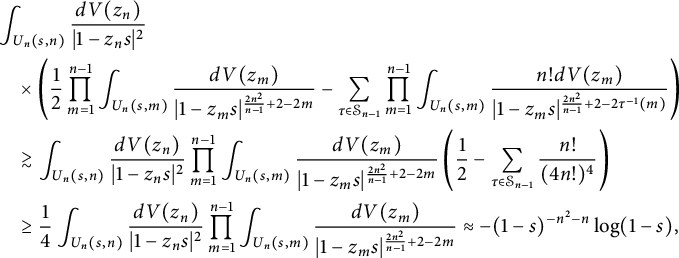 $$ \begin{align} &\int_{U_n(s,n)}\frac{dV(z_n)}{|1-z_ns|^{2}}\nonumber\\& \quad \times \left(\frac{1}{2}\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2m}}-\sum_{\tau\in\mathcal S_{n-1}}\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{n!dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2\tau^{-1}(m)}}\right)\nonumber\\& \quad \gtrsim \int_{U_n(s,n)}\frac{dV(z_n)}{|1-z_ns|^{2}}\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2m}}\left(\frac{1}{2}-\sum_{\tau\in\mathcal S_{n-1}}\frac{n!}{(4n!)^{4}}\right) \nonumber\\& \quad \geq \frac{1}{4} \int_{U_n(s,n)}\frac{dV(z_n)}{|1-z_ns|^{2}}\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2m}}\approx-(1-s)^{-n^2-n}\log(1-s),\nonumber\\ \end{align} $$
$$ \begin{align} &\int_{U_n(s,n)}\frac{dV(z_n)}{|1-z_ns|^{2}}\nonumber\\& \quad \times \left(\frac{1}{2}\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2m}}-\sum_{\tau\in\mathcal S_{n-1}}\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{n!dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2\tau^{-1}(m)}}\right)\nonumber\\& \quad \gtrsim \int_{U_n(s,n)}\frac{dV(z_n)}{|1-z_ns|^{2}}\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2m}}\left(\frac{1}{2}-\sum_{\tau\in\mathcal S_{n-1}}\frac{n!}{(4n!)^{4}}\right) \nonumber\\& \quad \geq \frac{1}{4} \int_{U_n(s,n)}\frac{dV(z_n)}{|1-z_ns|^{2}}\prod_{m=1}^{n-1}\int_{U_n(s,m)}\frac{dV(z_m)}{|1-z_ms|^{\frac{2n^2}{n-1}+2-2m}}\approx-(1-s)^{-n^2-n}\log(1-s),\nonumber\\ \end{align} $$
which implies that
![]() $\| \tilde T^n(h_s)\|^p_{L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2})}\gtrsim -(1-s)^{-n^2-n}\log (1-s)$
. Thus
$\| \tilde T^n(h_s)\|^p_{L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2})}\gtrsim -(1-s)^{-n^2-n}\log (1-s)$
. Thus
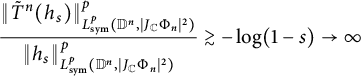 $$\begin{align*}\frac{\| \tilde T^n(h_s)\|^p_{L^p_{\text{sym}}(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2})}}{\|h_s\|^p_{L^p_{\text{sym}}(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2})}}\gtrsim-\log(1-s)\to \infty \end{align*}$$
$$\begin{align*}\frac{\| \tilde T^n(h_s)\|^p_{L^p_{\text{sym}}(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2})}}{\|h_s\|^p_{L^p_{\text{sym}}(\mathbb D^n,|J_{\mathbb C}\Phi_n|^{2})}}\gtrsim-\log(1-s)\to \infty \end{align*}$$
as
![]() $s\to 1$
, proving that
$s\to 1$
, proving that
![]() $\tilde T^n$
is unbounded on
$\tilde T^n$
is unbounded on
![]() $L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2})$
for
$L^p_{\text {sym}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2})$
for
![]() $p=\frac {2n}{n-1}$
.
$p=\frac {2n}{n-1}$
.
5 Some remarks
1. In [Reference Huo and WickHW20a], we studied weak-type estimates of the Bergman projection on the Hartogs triangle and showed the projection is of weak-type
![]() $(4,4)$
but not of weak-type
$(4,4)$
but not of weak-type
![]() $(\frac {4}{3},\frac {4}{3})$
. These results together with the Marcinkiewicz interpolation also recover the sharp
$(\frac {4}{3},\frac {4}{3})$
. These results together with the Marcinkiewicz interpolation also recover the sharp
![]() $L^p$
regular range
$L^p$
regular range
![]() $(\frac {4}{3},4)$
for the projection on the Hartogs triangle. Similarly, weak-type
$(\frac {4}{3},4)$
for the projection on the Hartogs triangle. Similarly, weak-type
![]() $(p,p)$
estimates of
$(p,p)$
estimates of
![]() $P_{\mathbb G^n}$
when
$P_{\mathbb G^n}$
when
![]() $p=\frac {2n}{n\pm 1}$
could lead to an alternative approach for Theorem 1.1.
$p=\frac {2n}{n\pm 1}$
could lead to an alternative approach for Theorem 1.1.
2. In [Reference Chen, Jin and YuanCJY23], Chen, Jin, and Yuan obtained the Sobolev
![]() $L^p$
boundedness for
$L^p$
boundedness for
![]() $P_{\mathbb G}$
from
$P_{\mathbb G}$
from
![]() $W^{k,p}(\mathbb G)$
to some weighted
$W^{k,p}(\mathbb G)$
to some weighted
![]() $W^{k,p}$
spaces for
$W^{k,p}$
spaces for
![]() $p>2$
. With
$p>2$
. With
![]() $L^p$
irregularity results obtained for
$L^p$
irregularity results obtained for
![]() $P_{\mathbb G^n}$
, it would be interesting to investigate the
$P_{\mathbb G^n}$
, it would be interesting to investigate the
![]() $W^{k,p}$
(ir)regularity for
$W^{k,p}$
(ir)regularity for
![]() $P_{\mathbb G^n}$
. In addition to estimates for
$P_{\mathbb G^n}$
. In addition to estimates for
![]() $P_{\mathbb G^n}$
, one may further consider
$P_{\mathbb G^n}$
, one may further consider
![]() $L^p$
boundedness and compactness of operators that are related to the Bergman projection, such as Toeplitz operators and Hankel operators.
$L^p$
boundedness and compactness of operators that are related to the Bergman projection, such as Toeplitz operators and Hankel operators.
3. The symmetrized polydisc
![]() $\mathbb G^n$
can be viewed as the quotient domain
$\mathbb G^n$
can be viewed as the quotient domain
![]() $\mathbb D^n/\mathcal S_n$
, where
$\mathbb D^n/\mathcal S_n$
, where
![]() $\mathcal S_n$
is the group of permutations of variables acting on
$\mathcal S_n$
is the group of permutations of variables acting on
![]() $\mathbb D^n$
. It is interesting to see whether our method can be generalized to obtain similar results on other quotient domains of
$\mathbb D^n$
. It is interesting to see whether our method can be generalized to obtain similar results on other quotient domains of
![]() $\mathbb D^n$
. For instance, the
$\mathbb D^n$
. For instance, the
![]() $L^p$
norm of
$L^p$
norm of
![]() $P_{\mathbb G^n}$
is equivalent to the
$P_{\mathbb G^n}$
is equivalent to the
![]() $L^p$
norm of
$L^p$
norm of
![]() $P_{\mathbb D^n}$
over
$P_{\mathbb D^n}$
over
![]() ${L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})}$
, a subspace of
${L^p_{\text {anti}}(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})}$
, a subspace of
![]() $L^p(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
that is related to
$L^p(\mathbb D^n,|J_{\mathbb C}\Phi _n|^{2-p})$
that is related to
![]() $\mathcal S_n$
. On this subspace, we are able to construct the operator
$\mathcal S_n$
. On this subspace, we are able to construct the operator
![]() $T^n_2$
which equals
$T^n_2$
which equals
![]() $P_{\mathbb D^n}$
. It is interesting to see if such a proving strategy can be abstracted to work for general quotient domains.
$P_{\mathbb D^n}$
. It is interesting to see if such a proving strategy can be abstracted to work for general quotient domains.
Acknowledgments
The authors would like to thank Gian Maria Dall’Ara, Yuan Yuan, Yuan Zhang, Włodzimierz Zwonek, and the anonymous referee for their valuable comments and suggestions.